一题多变,探寻教材例题的教学价值
2016-04-13江苏省南京市溧水区孔镇中学杨绍平
☉江苏省南京市溧水区孔镇中学 杨绍平
一题多变,探寻教材例题的教学价值
☉江苏省南京市溧水区孔镇中学杨绍平
一题多变是通过题目的引申、变化、发散,提供问题的背景,揭示问题间的逻辑关系,课堂上“一题多变”的适当运用,不仅可以加深学生对所学知识的理解,还能激发学生的探究精神和学习热情,更能达到拓展数学思维的作用.下面以苏科版义务教育课程标准实施的教科书数学九年级上册第四章“一元二次方程”第1.4节“用一元二次方程解决问题(3)”为例加以说明.
一、课堂实录
1.例题呈现
如图,在矩形ABCD中,AB=6cm,BC= 12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C 以2cm/s的速度移动,问:几秒后△PQB的面积等于8cm2?

2.教学过程
本题对学生来说求解不是很困难.
解:设x秒后△PQB的面积等于8cm2.(以下x都表示运动时间)
解这个方程,得:x1=2,x2=4.
答:2秒或4秒后△PQB的面积等于8cm2.
师:大家做的很好,如果我换一个问题,你能解决吗?
生1:(利用前一问的经验,很快便有了答案)在Rt△PQB中,运用勾股定理,得
师:回答的很好,看来这两个题目都难不到你们,我再来换一个问题看看你们是否也能解决.
(板书变式2:若题目条件不变,几秒后△PQD的面积等于28cm2?)
(片刻后)师:谁来说说你怎么思考的?

师:你们同意吗?
(学生们都面面相觑,有些小声赞成,也有几位同学表示反对)
师:这么多同学赞成,你却反对,说说你有什么高见.
生3:刚才生2这样列方程其实默认了∠PQD=90°,题目中并没有这个条件.
(生2脸有点红,也意识到自己错了)
师:你们同意吗?
(众生表示同意,并对生3啧啧称赞.)
师:那么此题该如何解决呢?
生4:之前我们学习过利用“割补法”来求不规则图形的面积,那么对于此题也可试试看,即:S矩形ABCD-S△DAPS△PBQ-S△QCD=S△PQD,于是根据题意可列方程:
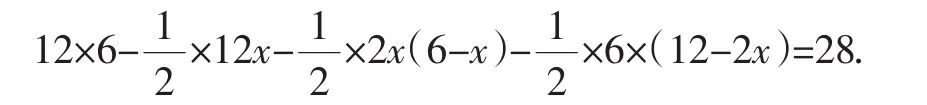
师:看来我们要认真审题,要从已知条件出发,切不可被图形迷住了双眼而硬生生地添加条件,其实此处利用“割补法”求△PQD的面积也正是我们常说的“化斜为直”.(生3感到很开心,生2就显得有点消沉.)但我要特别感谢生2,他让我想到了另一个问题.
(板书变式3:若题目条件不变,几秒后DQ⊥PQ?)
(看到生2脸又红了,微微一笑.笔者心想:老师的一句话既能解除生2的尴尬,又能活跃课堂气氛,看来当好一名老师真的很重要)
生5:在Rt△DPQ中运用勾股定理列出方程[(6-x)2+ (2x)2]+[62+(12-2x)2]=122+x2.
(学生边说,教师边板书,并有意将方程写的很长)
师:生5灵活利用勾股定理解决此题,的确很妙.但我对他有意见,这个方程写下来好累呀!你们累吗?有没有更加简洁的方法?
(这时的课堂气氛及学生的学习状态都非常好,思考片刻便有好几个学生举手)

师:不比不知道,一比吓一跳.我们平时不仅要追求正解,还要思考有没有其他解法,有没有其他更简洁的方法,不同的人在数学上有不同的收获.我现在又要感谢生6了,他又让我想到另一个问题.
(板书变式4:若题目条件不变,几秒后△DCQ与△QBP相似?)
(学生的学习热情已被激发出来了,能积极主动地进行探讨,有学生说不是跟上题一样吗?)
师:(追问一句)真的一样吗?下面你们就小组讨论到底是否相同.
(3分钟后,小组代表汇报结论)

师:你还能对题目进行怎样的改编?
(思考片刻后有学生陆续举手)
生8:若题目条件不变,几秒后△DPQ是等腰三角形?
师:很好,你们能解决吗?
生9:我觉得很简单,如图1,由DP=DQ,得DP2=DQ2,即:
x2+122=62+(12-2x)2.
(底下窃窃私语,有不少学生举手表示有不同意见)
生10:根据题目的意思,只要△DPQ是等腰三角形即可,所以要进行分类讨论,除了生9叙述的情况外,应还有:
当QP=QD时,有(6-x)2+(2x)2=62+(12-2x)2;
当PD=PQ时,有x2+122=(6-x)2+(2x)2.
师:很好,我们考虑问题一定要全面,遇到等腰三角形的题目很有可能需分类讨论.
(正当笔者小结时又有一个学生举起了手)

(众生赞叹!一起鼓掌)
师:真了不起,我们要向生11学习,养成认真勤奋、反思质疑等良好的学习习惯.
师:今天大家参与的非常积极,肯定有不少收获,你们谈谈自己的感想吧!
生12:数学真的挺有意思的,同样一个题目可以变化成这么多问题,也考查了这么多数学知识……
二、几点思考
从一个例题的展开,学生既能掌握所学知识,又能在探索与获取知识的过程中感受数学的“美”.既培养学生学习数学的兴趣,又增强学好数学的信心.这节课下来,笔者也有以下几点思考.
1.提高解题能力
《数学课程标准(2011年版)》(以下简称“课标”)明确指出:获得分析问题和解决问题的一些基本方法,体验解决问题方法的多样性,发展创新意识.本节课在每个变式得到解答后,笔者都注意引导学生对题目进行比较,对解题方法进行思考,及时总结、概括知识间的内在联系,力求达到“解一题,会一片,通一类”的效果.如上述案例中,可让学生总结出解决动态变化题的一些策略,如:化动为静,求线段长度通常利用勾股定理和相似,求面积可分为直接求和间接求(割补法)两种,等腰三角形问题往往需要进行分类讨论等.
2.拓展学生思维
“一题多变”是培养学生思维品质的有效途径之一.通过一题多变的训练,可以使学生认清各个变式题之间的联系和区别;可以开拓学生解题的思路,训练学生归纳总结、勇于探索的意识;有利于培养学生的发散思维能力,能进一步深化对知识的理解和掌握,从而提高课堂教学效率.另外,在教学过程中通过引导学生对不同方法进行比较,优化他们的解题思路,这也拓展了他们的思维.例如在变式3“若题目条件不变,几秒后DQ⊥PQ?”解决过程中,有学生利用勾股定理构造方程,也有学生利用三角形相似来构造方程,使学生明白一题可能有多种解法,通过比较选择最优化方案.
3.引发探究热情
“课标”明确指出:学生获得知识,必须建立在自己思考的基础上,可以通过接受学习的方式,也可以通过自主探索等方式;学生应用知识并逐步形成技能,离不开自己的实践;学生在获得知识技能的过程中,只有亲身参与教师精心设计的教学活动,才能在数学思考、问题解决和情感态度方面得到发展.本节课笔者能利用亲切、感人的教学语言唤起学生的热情;努力营造师生互动、生生互动、生动活泼的课堂氛围;以平等、尊重的态度鼓励学生积极参与教学活动,启发学生共同探索,与学生一起感受成功与挫折、分享发现和结果.在经历了一系列的变式训练后,笔者灵机一动抛出了“你还能对题目进行怎样的改编?”这一问题,此时学生的积极性及探究热情被充分地调动起来,也体现了“课标”中的理念:初步学会从数学的角度发现问题和提出问题,综合运用数学知识解决简单的实际问题,增强应用意识,提高实践能力.
总之,在课堂教学中,应根据教学目标,结合具体学情,采用适当的教学方法创造性地使用教材例题,对其进行一题多变,从而激发学生的求知欲,教给学生探究的方法和策略,挖掘“变”中的“不变”,努力探寻教材例题的教学价值,培养学生科学的探究精神.
参考文献:
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.何君青.例谈数学课堂教学中的“一题多变,一题多问”[J].中学数学(下),2010(10).
3.黄圣清.巧用“一题多变”培养数学思维[J].上海中学数学,2015(1-2).
