探究一道中考选择题的解法
2016-04-13浙江省浦江县实验中学
☉浙江省浦江县实验中学 方 芳
探究一道中考选择题的解法
☉浙江省浦江县实验中学方芳
题目(2014年湖北武汉)如图1,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB 于C、D两点.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是().
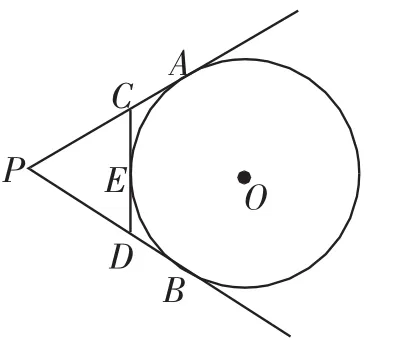
图1
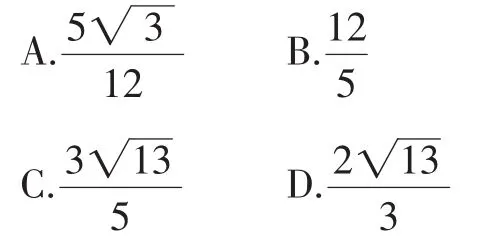
分析:此题以圆的一个基本图形为背景设置,内涵十分丰富:PA=PB;连接OA、OB,则∠OAP=∠OBP=90°;连接OP,则OP平分∠APB;连接AB,则OP垂直平分AB……
又CD切⊙O于点E,所以CA=CE,DB=DE.
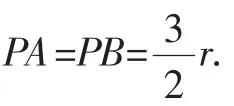
一、直接法
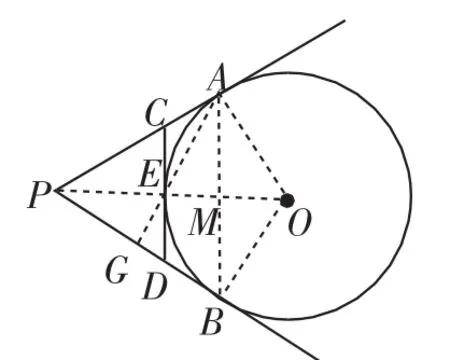
图2
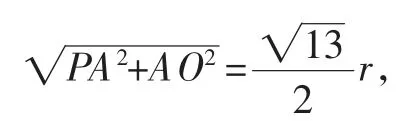
二、转化法
注意到∠APB=2∠APO,可利用Rt△PAO斜边上的中线构造一个与∠APB相等的角,求出这个角的正切值即可.
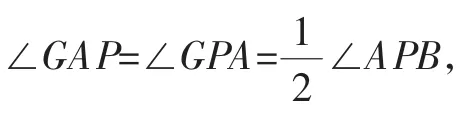
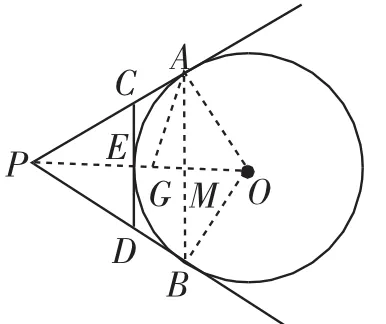
图3

三、割补法
连接OA、OB得到一个一组对角为直角的四边形,不妨把这种四边形称为“双垂四边形”,它是一种特殊的四边形,在已知和未知难以直接产生关系时,通常采取用“割”与“补”的方法来添加辅助线,将其转化为熟悉的图形来求解.
1.补成直角三角形+相似三角形
解法3:如图4,延长BO交PA的延长线于点F,则△PBF为直角三角形.
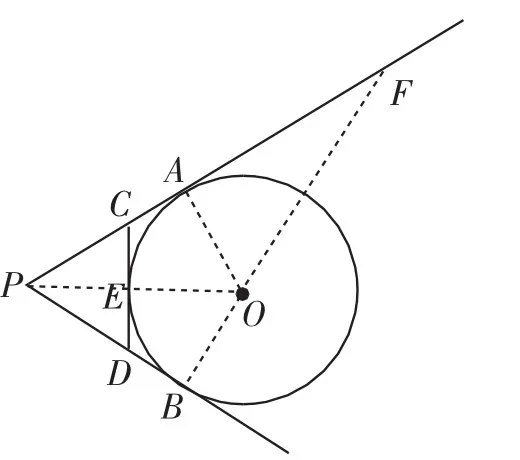
图4
因为BF=BO+FO,
2.补成矩形+相似三角形
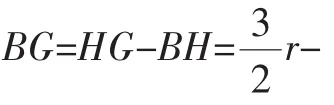
所以故选B.
3.割成矩形+相似三角形
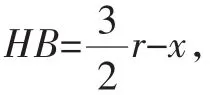
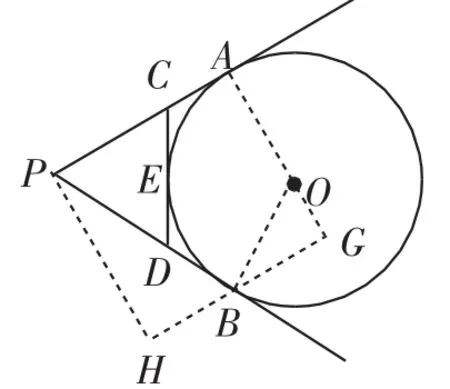
图5
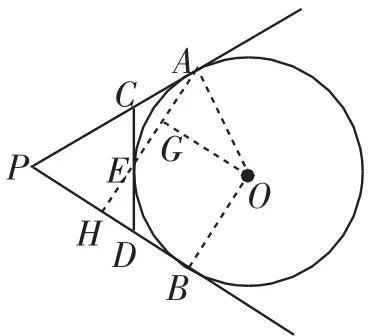
图6
四、倍角法
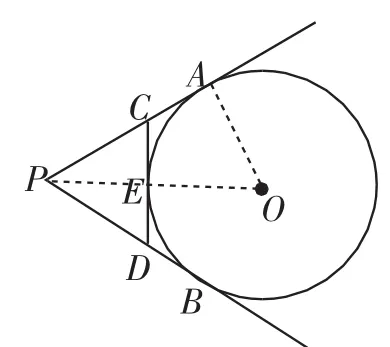
图7
注意到∠APB=2∠APO,而∠APO是Rt△APO的一个锐角,用高中倍角公式可直接求解,方法十分简洁.
解法6:如图7,连接PO,则∠APB=2∠APO.
从这道中考选择题的初中解法看,尽管所添的辅助线不同,但都体现了一种共同的思想──转化思想,几种解法都用到了一些基本图形性质,如直角三角形、等腰三角形、矩形,以及全等三角形、相似三角形等基础知识.带给我们的教学启示是:即使是比较复杂的问题,所用到的知识也是基础知识的组合和数学思想方法的凸现,这就要求教师在日常教学中,尤其在中考复习阶段,不仅要精挑典型问题、教给学生解题方法,而且还应与学生共同探究有哪些解法,让学生说出“为什么这样想”,“用到哪些知识”,“哪种解法更自然”,“哪种方法更简洁”,“同样的方法能用来处理更一般性的问题吗”,“这些方法体现了什么样的数学思想”,潜移默化地增强学生解题的信心、提升解题能力.在课堂教学中,教师不能只当“二传手”的角色,而要用心去思考、去变化,用智慧去整合、去创新,唯有如此,学生才能受益无穷.
