层间隔震体系可靠度的灵敏度分析*

张尚荣， 谭 平， 杜永峰， 周福霖， 包 超

(1.兰州理工大学防震减灾研究所 兰州，730050) (2.广州大学工程抗震研究中心 广州，510405) (3.宁夏大学土木与水利工程学院 银川，750000)

层间隔震体系可靠度的灵敏度分析*

张尚荣1,3， 谭 平2， 杜永峰1， 周福霖2， 包 超1

(1.兰州理工大学防震减灾研究所 兰州，730050) (2.广州大学工程抗震研究中心 广州，510405) (3.宁夏大学土木与水利工程学院 银川，750000)

考虑层间隔震体系(上部隔震结构、中间层隔震结构、下部隔震结构)随机参量和地震激励的不确定性，利用随机响应面方法，结合基于线性无关原则的概率配点方法，将隐式的结构响应函数转换成显式函数，在此基础上利用Monte-Carlo分别对3种隔震结构形式可靠度进行分析，并分析了其对应的可靠度灵敏度。结果表明：层间隔震体系中，各随机变量均值变化对体系的可靠度将会产生不同的影响，各随机变量方差的增加都将降低体系的可靠度；可通过优化设计变量，严格控制施工质量(控制变量方差)，降低其对体系可靠度的影响。可靠度灵敏度的分析结果可以提供体系的可靠度指标对随机参量变化的重要性排序，从而提高大型复杂结构的可靠度分析和优化设计的效率,同时为层间隔震体系可靠度灵敏度的进一步研究奠定基础。

层间隔震体系； 随机响应面法； 线性无关概率配点； 首超破坏准则； 可靠度灵敏度

引 言

工程结构系统的安全可靠是结构系统设计的主要目的之一。层间隔震结构体系作为一种新型的结构体系，其结构物理参数具有分散性，承受的载荷带有随机变化的性质，从而导致了具有随机参数的随机层间隔震结构体系。因此，研究这种结构系统的可靠性和可靠性灵敏度问题有重要的意义[1]。通过灵敏度分析，可以确定调整何种设计参数最为有效，从而选取尽量少的优化变量，帮助工程技术人员合理地建立结构系统安全容限和控制随机参数。

对工程结构可靠性灵敏度的研究，自文献[2]提出特征值和特征向量灵敏度以来，已有很多学者对机电工程领域的灵敏度问题进行了研究[3-4]。传统的多项式响应面法在结构可靠性分析中占有重要的地位，但其结果容易受到拟合函数形式及拟合点位置的影响，限制了响应面法对极限状态函数的近似程度[5]。文献[6]提出随机响应面法(stochastic response surface method, 简称SRSM)，并将其用于环境和生物学等领域中的概率分析。层间隔震体系作为一种新型的结构体系，隔震层位置设置的不同，结构表现出不同的工作机理，影响结构可靠度的主要参量也不同，因此研究隔震层位置变化而影响结构可靠度的主要参量对层间隔震体系的经济性和安全性具有重要意义。笔者将随机结构可靠性灵敏度分析引入层间隔震结构体系，研究体系中各随机变量或其参数变化对可靠度的影响规律，从而为各随机变量或参数之间的重要性程度提供横向对比，对层间隔震体系的可靠性设计、修改、优化等方面具有指导意义。

1 层间隔震体系随机响应分析

在线弹性情况下，图1为层间隔震体系计算模型，其运动方程为

(1)

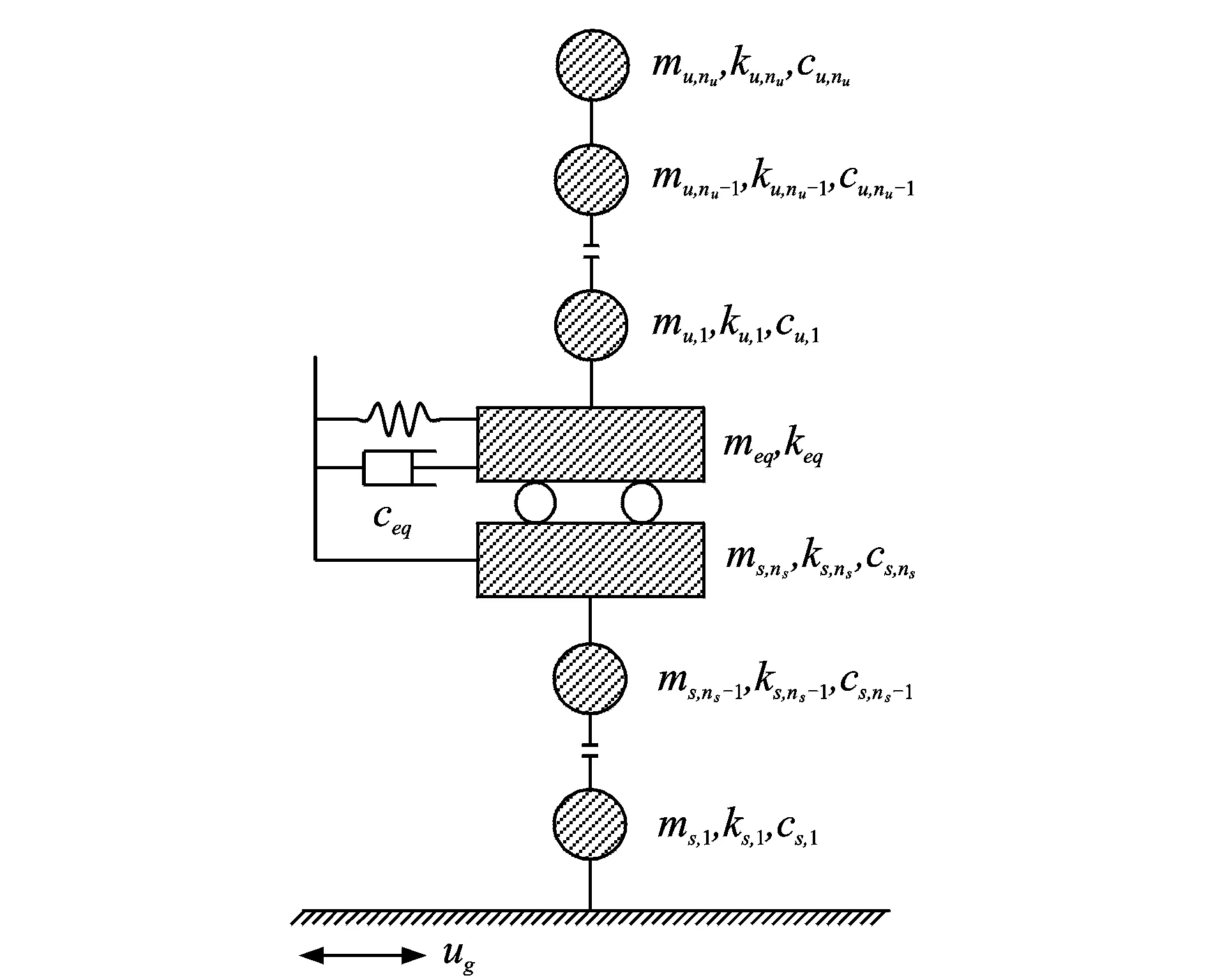
图1 层间隔震体系计算模型Fig.1 Calculation mode of inter-story isolated system

层间隔震体系是典型的非经典阻尼体系，其阻尼矩阵不能在N维主空间中解耦。笔者采用复模态方法对其进行动力特性分析。

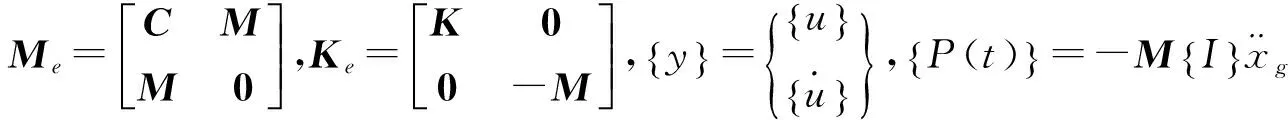
(2)

式(2)对应的特征矢量方程为

(3)

复模态质量为

复模态刚度为

将状态量用复模态表示并代入式(3)，经傅里叶变化可得传递矩阵

(4)

(5)

结构位移响应功率谱可表示为

(6)

结构位移响应方差为

(7)

2 随机响应面模型的建立

随机响应面法[8]是基于具有平方可积概率密度函数的随机变量可以表达为独立标准分布随机变量的函数形式假定，将输入随机变量转换为独立同分布的标准正态随机变量的函数，并利用独立标准正态随机变量的混沌多项式来描述随机响应。

(8)

随机响应面法的结果取决于待估参数bi1,bi1i2，…，bi1i2…in的求解中概率配点的选择。一般来说，p阶随机多项式展开配点是通过p+1阶Hermite多项式的根确定[9]，且按照此方法确定的可供选择的配点数目N远远大于所需配点Nc的数目。笔者采取基于线性无关原则选取概率配点，剔除了大量线性相关配点，保证混沌多项式系数矩阵按行线性无关，且系数矩阵为行满秩矩阵，待定系数有唯一解。这样既确保计算结果的稳定性，又提高了计算效率。

以上的样本点均在标准正态空间内，根据需要将其转换到原始空间。笔者选取变量均假定服从正态分布，其转换形式为

(10)

其中：μi，σi分别为变量xip的均值和标准差。

转换后的原始空间样本点形成试验样本，通过动力分析方法得到结构的真实响应，用最小二乘法求解线性方程组得到待定系数，即得到随机响应面模型的显式表达函数。

(11)

(12)

其中：B为待估参数系数矩阵；X为Hermite多项式组合矩阵；Y为响应矩阵；k为模型验证的样本数量；p为随机变量数量。

3 层间隔震体系可靠度灵敏度分析

3.1 基于首超破坏的动力可靠度

结构受地震作用动力可靠度分析是典型的基于首次穿越破坏分析,假定地震激励和结构响应为零均值平稳随机过程。记ye和σy分别为结构响应y(t)的极值(绝对最大值)和标准差，定义无量纲参数[10]为

(13)

根据水平跨越次数是Poisson过程的假定，求得极值的概率分布为

(14)

(15)

η的极值标准差为

(16)

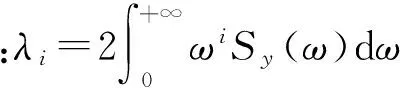
随机过程y(t)的极值的期望值表示为

(17)

层间隔震体系以层间位移角极限状态表示的状态方程为

(18)

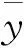
可靠性指标定义为

(19)

若y(x)服从正态分布，得到可靠度

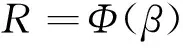
(20)

3.2 可靠度灵敏度

可靠度灵敏度反映设计参数的改变对失效概率的影响程度，常常为结构可靠度优化设计确定最优解的搜索方向，是结构可靠度优化设计的重要组成部分[11]。笔者在SRSM生成显式函数的基础上建立了基于Monte-Carlo模拟的可靠度灵敏度分析方法，基本随机参数矢量的均值矩阵μ和方差矩阵D的灵敏度为

(21)

(22)

其中

(23)

4 仿真分析

以两自由度等效模型通过NSGA-Ⅱ优化分析，得到以基底剪力最小为优化目标的层间隔震体系在不同质量比下的最优频率比和最优阻尼比作为算例模型。

4.1 遗传优化算法—NSGA-Ⅱ

NSGA-Ⅱ在选择过程中采用非支配排序降低了计算复杂度，加快了收敛速度。形成支配集后引入的精英策略提高了结果的优化精度与种群水平。同时加入的拥挤度处理等方法保证了种群的分布性与多样性。经过交叉变异等操作直到指定最大代数后终止，解集的收敛性好且易于得到全局最优解的优点，成为其他多目标优化算法性能的基准。

4.2 工程算例

通过NSGA-Ⅱ优化分析，结构在不同质量比下的最优频率比和最优阻尼比的结果如表1所示，上、下部子结构的阻尼比取为0.05；上、下部子结构的高度分别均为2.7 m和3.3 m； 结构的随机激励模

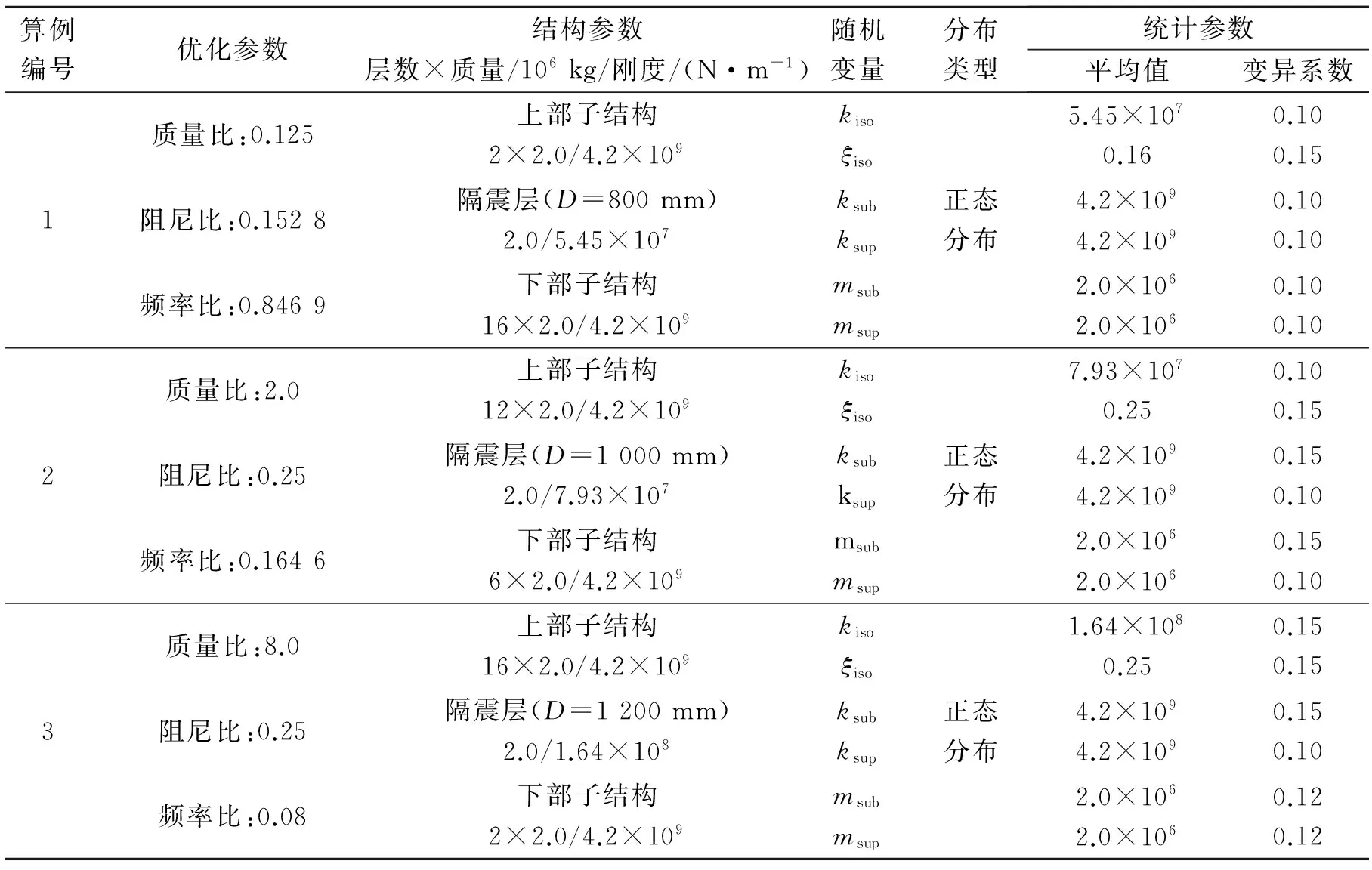
表1 结构参数统计信息

型采用Clough-Penzien谱[12]，谱强度因子S0=9.537 cm2/s3；地基土卓越频率和阻尼比ωf和ξf分别为ωf=17.95 rad/s，ξf=0.72；ωc和ξc分别取ωc=0.1-0.2ωf，ξc=ξf。

假定结构随机变量为隔震层刚度kiso，隔震层阻尼比ξiso，上、下部子结构刚度ksup，ksub，上、下部子结构质量msup，msub，上部子结构质，且假定以上各随机变量均服从正态分布，其均值和变异系数如表1所示。小震下，各楼层层间的位移角限值[13]取为dmax=1/550 rad；隔震层的水平位移限值不应超过隔震支座有效直径的0.55倍和支座橡胶总厚度3.0倍二者中的较小值(这里假定前者小于后者，即选取0.55d作为限值)。大震下，考虑到层间隔震体系的非线性问题及可靠度指标选取的复杂性，笔者仅对体系在小震下的可靠性灵敏度进行分析，为大震下体系可靠度灵敏度研究奠定基础。

4.3 结果分析

根据各随机变量在结构中变异程度概率大小给予变量不同的变异系数，如表1所示。利用随机响应面方法并根据式(8)，(10)分别得到层间隔震结构体系的层间位移角极值的随机响应面函数。限于篇幅，仅给出层间隔震体系质量比μ=2.0(中间层隔震结构)的随机响应面函数。

(24)

其中

-0.39,774,1550 }

1.10×10- 3,3.03,-2.97,5.33×104,

3.71×105, -8.09×106, 1.78×107,

-6.72×10-5,-0.156,0.0307,

-0.0412,-0.196,310 }

对随机响应面函数应用Monte Carlo模拟得到层间隔震体系状态函数的概率统计参数[14]，如表2所示。结合随机响应面显式函数的概率统计参数，两者模拟所得数据相近。

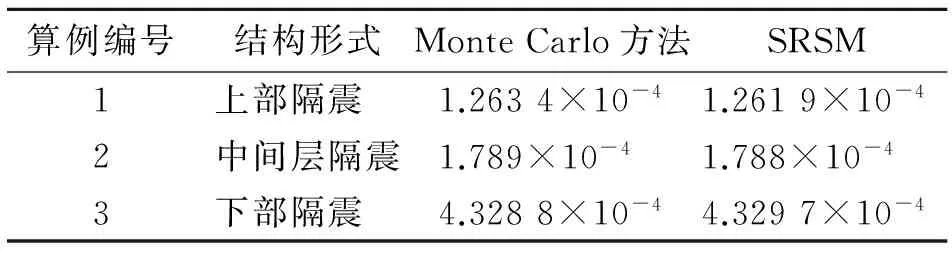
表2 随机响应面函数概率统计信息(极限状态均值)

表3和图2为考虑体系各随机变量变异系数时，层间隔震体系可靠度灵敏度的计算结果。可以看出：层间隔震体系中，隔震层阻尼比ξiso的增加，增加了结构的阻尼耗能，从而提高了体系的可靠度。对于中间层隔震结构，隔震层刚度kiso和上部子结构刚度ksup的增加，提高了结构的可靠性，而下部子结构刚度ksub及上、下部子结构质量的增加，将使结构可靠度有所降低。从影响程度上看，中间层隔震结构各随机变量均值的可靠度灵敏度排序，即各参数之间重要性程度为：隔震层阻尼比、上部子结构刚度、隔震层刚度、下部子结构刚度、下部子结构质量和上部子结构质量。同理，得到上部隔震和下部隔震结构各参数之间重要性程度。另外，各随机变量方差的增加都将降低体系可靠度。因此，对于层间隔震体系，通过在设计中优化随机变量的均值以及施工中严格控制施工质量(控制各变量方差)，降低其对可靠度的影响。

表3 层间隔震体系可靠性灵敏度分析结果

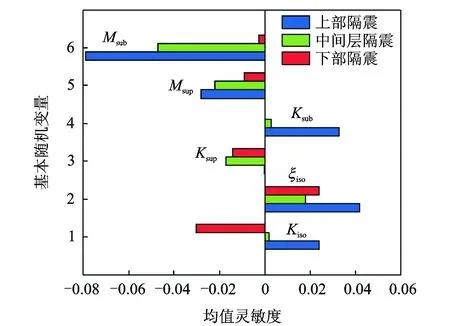
图2 可靠性极值均值灵敏度Fig.2 Reliability sensitivity of extremum average

5 结 论

1) 层间隔震体系中，上部子结构和下部子结构刚度的变化对整体结构的可靠度将产生不同影响，在体系设计中应严格控制上、下部子结构刚度，从而降低其对结构可靠度的影响。

2) 随机参量方差对层间隔震体系可靠度的灵敏度总体表现为各随机变量方差的增加都将降低体系的可靠度。因此在结构施工阶段，应严格控制施工质量，降低其对体系可靠度的影响。

3) 层间隔震体系可靠度的灵敏度分析结果可以提供体系的可靠度指标对随机参量变化的重要性排序，对影响较小的参量可以作为定量处理，可以提高大型复杂结构可靠度分析和优化设计的效率。

4) 仅分析了层间隔震体系“小震”下的变形能力可靠度的灵敏度，还需验算其在“中震”和“大震”下的变形能力和极限承载能力的可靠度灵敏度，该方法为层间隔震体系可靠度灵敏度的进一步研究奠定了基础。

[1] 张义民，刘巧伶. 单自由度非线性随机参数振动系统的可靠性灵敏度分析[J]. 固体力学学报，2003, 24(1)：61-67.

Zhang Yimin, Liu Qiaoling. Reliability sensitivity analysis of single degree-of-freedom nonlinear vibration systems with random parameters[J]. Acta Mechanica Solida Sinica，2003, 24(1)：61-67. (in Chinese)

[2] Fox R L, Kapoor M P. Rates of change of eigenvalues and eigenvectors[J]. AIAA Journal, 1968, 6 (12): 2426-2429.

[3] Robert H S, Mark A C. System reliability and sensitivity factors via the MPPSS method[J]. Probabilistic Engineering Mechanics, 2005,20(2):148-157.

[4] 卢昊，张义民，赵长龙,等.多失效模式机械零件可靠度灵敏度估计[J].机械工程学报，2012, 48(2)：63-67.

Lu Hao, Zhang Yimin, Zhao Changlong, et al. Reliability sensitivity estimation of mechanical components with multiple failure modes[J]. Journal of Mechanical Engineering, 2012,48(2)：63-67. (in Chinese)

[5] 李洪双，吕震宙，赵洁. 基于加权线性响应面法的支持向量机可靠性分析方法[J]. 工程力学，2007, 24(5)：67-71.

Li Hongshuang, Lü Zhenzhou, Zhao Jie. A support vector machine method for reliability analysis based on weighted linear response surface[J]. Engineering Mechanics, 2007, 24(5)：67-71. (in Chinese)

[6] Isukapalli S, Roy A, Georgopoulos P. Stochastic response surface methods(SRSM) for uncertainty propagation: application to environmental and biological systems[J]. Risk Analysis, 1998, 18 (3): 351-363.

[7] 杜永峰，张尚荣，李慧. 多级串联非比例阻尼隔震结构地震响应分析[J]. 西北地震学报, 2012, 34(4): 319-323.

Du Yongfeng, Zhang Shangrong, Li Hui. Seismic response analysis on multistage series non-proportion damping isolated structure[J]. Northwestern Seismological Journal, 2012, 34(4): 319-323. (in Chinese)

[8] 胡冉，李典庆，周创兵,等.基于随机响应面法的结构可靠度分析[J].工程力学，2010, 27(9)：192-200.

Hu Ran, Li Dianqing, Zhou Chuangbing, et al. Structural reliability analysis using stochastic response surface method[J]. Engineering Mechanics, 2010, 27(9)：192-200. (in Chinese)

[9] Isukapalli S S. An uncertainty analysis of transport transformation models[D]. New Brunswick : The State University of New Jersey, 1999.

[10]朱位秋.随机振动[M].北京:科学出版社,1998:492-502.

[11]乔红威，吕震宙.随机激励下随机结构动力可靠性灵敏度分析[J].振动工程学报,2008,21(4):404-408.

Qiao Hongwei, Lü Zhenzhou. Dynamic reliability sensitivity analysis for stochastic structures under random excitations[J]. Journal of Vibration Engineering, 2008, 21(4): 404-408. (in Chinese)

[12]薛素铎，王雪生，曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报,2003,36(5):5-10.

Xue Suduo, Wang Xuesheng, Cao Zi. Parameters study on seismic random model based on the new seismic code[J]. China Civil Engineering Journal, 2003, 36(5): 5-10. (in Chinese)

[13]中华人民共和国行业标准. GB50011-2010建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[14]王倩倩，张义民，王一冰,等.复合随机振动系统的动态可靠性分析[J].振动、测试与诊断,2013,33(4):670-675.

Wang Qianqian, Zhang Yimin, Wang Yibing, et al. Dynamic reliability analysis of double random vibration system[J]. Journal of Vibration , Measurement & Diagnosis, 2013, 33(4): 670-675. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.01.017

*国家重点基础研究发展计划(“九七三”计划)资助项目(2012CB723300,2012CB723304)；国家科技支撑计划子课题资助项目(2012BAJ07B02)；国家自然科学基金重点资助项目(91315301-07)；国家自然科学基金资助项目(51078097,51178211)；广州市羊城学者科技计划资助项目(10A032D)

2014-02-20；修回日期：2014-05-22

TU352.1

张尚荣，男，1984年12月生，博士研究生。主要研究方向为结构减震控制。曾发表《基于响应面法的层间隔震结构地震易损性分析》(《振动与冲击》2014年第33卷第15期)等论文。 E-mail:confidence.5@163.com 通信作者简介：谭平，男，1973年9月生，博士、教授。主要研究方向为结构减振控制。 E-mail:ptan@gzhu.edu.cn