基于模型参考自适应的永磁同步电机速度观测器中PI参数调节方法*

刘小俊， 张广明， 梅 磊， 王德明

(南京工业大学 电气工程与控制科学学院，江苏 南京 210009)

基于模型参考自适应的永磁同步电机速度观测器中PI参数调节方法*

刘小俊， 张广明， 梅 磊， 王德明

(南京工业大学 电气工程与控制科学学院，江苏 南京 210009)

永磁同步电机(PMSM)在有感控制方案中需安装编码器或霍尔传感器，增加了系统的设计成本，因此，研究PMSM的无感控制方案就显得有必要性。随着现代控制理论的发展，无传感器技术也日益发展。以磁场定向控制为控制策略，以模型参考自适应理论为基础，设计了一种速度观测器。侧重用现代控制理论知识分析了观测器的稳定性，并用传统控制理论知识分析了一种新的观测器中PI调节器参数整定方法。这种方法具有很强的适应性和移植性。最后，验证了这种方法的准确性和可行性。

永磁同步电机； 无感控制； 模型参考自适应系统； 稳定性； 参数整定

0 引 言

近年来，随着电力电子技术的发展，交流伺服系统越来越受到人们的关注。其中永磁同步电机(Permanent Magnet Synchronous Motor， PMSM)具有体积小、效率高、功率密度高等特点，在交流伺服系统中占据着重要的地位，在高性能驱动系统中得到了广泛的应用[1-3]。目前，PMSM的驱动通常使用磁场定向控制(Field Oriented Control， FOC)或者直接转矩控制(Direct Torque Control， DTC)。但是，无论是针对哪种控制策略，都需要用到转速和转子位置角信息。当然，这两个参数知道其中一个即可。目前，对于这两个参数的获取有两种方案，即有传感器和无传感器。在有感方案中，需要在电机上安装编码器或者霍尔传感器等，能直接获取位置信息。但这种方案无疑增加了系统的设计成本，适应性也较弱。在无感方案中，最先提出也是最简单的方法是反电动势法，但是在低速时，反电动势小导致精度不高。另一种比较成熟的方法是高频信号注入法，这种方法依赖外部激励，还要求电机本身具有凸极性，在高速时不适用。随着现代控制理论的发展，滑模观测器、自适应律、卡尔曼滤波器等无感方案也发展起来[4-5]。这些方法对外部扰动不敏感，鲁棒性好，进而受到越来越多研究者的关注。

模型参考自适应系统(Model Reference Adaptive System， MRAS)具有算法简单、易于在数字控制系统中进行实现、有比较快的自适应速度等优点，已经被提出并应用在无感PMSM控制中[6]。其速度信息是通过两种不同的模型获取的： 一种是参考模型，即电机本体，其与速度信息无关；另一种是可调模型，即计算模型，包括速度信息。将两个模型输出量的偏差信号传至自适应机构，自适应机构的输出为速度信号[7]。从目前研究来看，MRAS方法估计速度信号的重点是可调模型的建立以及自适应机构中自适应律的构建。这两者关系着估计速度的精度和系统的稳定性。一般自适应律都包含PI调节器，但是目前很多文献对于PI参数的给定没有作出详细说明，仅单纯地给个数值。因此，本文对PI调节器的参数问题展开研究。

文献[8-11]给出了MRAS理论用于估计PMSM速度的基本理论知识，讲述了以定子电流的交轴(q轴)和直轴(d轴)方程为可调模型，以波波夫(Popov)超稳定性理论构建了自适应律，给本文奠定了理论基础。文献[12]在负载变化的情况下使用MRAS作无感控制，充分说明了MRAS的鲁棒性好的特点。文献[13]在MRAS理论的基础上，对比了传统PI、模糊PI及粒子群优化的控制方法，可以看出MRAS理论的适应性强。文献[14]在MRAS理论基础上，使用模糊控制器来调节观测器中的PI调节器参数，使得整个系统在很宽的速度范围内具有很好的动稳态性能。文献[15]基于MRAS理论，用神经网络调节两个模型的误差而得出速度信息，故精度较高、静态和动态性能好。文献[16]分别以波波夫超稳定性和李雅普诺夫稳定性分析法构建了自适应律，并作了对比。同样文献[17]以准梯度算法构建了自适应律。自适应律不同，系统的性能也都不同。文献[18]以现代控制理论知识分析了MRAS系统的稳定性，构建了系统的传递函数，并对其进行分析。在此基础上还辨识了定子电阻。文献[19]是以MRAS理论做了磁链观测器，并以现代控制理论知识分析稳定性，通过传递函数的零极点来调整观测器中PI调节器的参数。

本文在以上参考文献的基础上，针对速度观测器中PI参数调节问题展开研究。首先是以定子的d、q轴电流方程为可调模型，然后通过波波夫超稳定性构建了自适应律，用现代控制理论知识分析了其稳定性。最后构建了系统的传递函数，将观测器中PI调节器作为可调环节，用根轨迹分析法来调节PI的比例积分系数。这种方法简单有效，避免了文献[14]中使用模糊PI的复杂算法。针对不同参数的电机模型，都可以使用这种方法快速地定位出观测器中PI调节器的参数。通过仿真可以验证这种方法的准确性和有效性。

1 MRAS速度观测器

1.1 表贴式PMSM数学模型

表贴式PMSM在d、q坐标系下的定子电压方程为

(1)

式中：ud、uq、id、iq——电机在d、q轴下的定子电压和电流；

Rs、Ld、Lq——定子电阻和在d、q轴下的电感；

D——微分算子；

ωr、ψr——转子电角速度和磁链。

1.2 基于MRAS的速度观测器设计

根据式(1)可得定子电流状态方程：

(2)

对于表贴式PMSM有：Ld=Lq=Ls。以电机本体为参考模型，以式(2)为可调模型，可得参数可调的可调模型：

(3)

定义状态误差为

(4)

则式(2)减去式(3)的状态误差方程为

(5)

写成状态空间表达式：

D[ε]=[A][ε]+[B]u

(6)

1.3 速度观测器自适应律设计

MRAS基本框图如图1所示。

图1 MRAS基本框图

自适应机构的构建关系着系统的稳定性和精度。由图1可看出自适应机构和状态误差方程式(5)相关。关于式(5)的结构图如图2所示。

图2 式(5)结构图

对条件一，可根据现代控制理论知识推导前向通道的传递函数，状态空间表达式为

(7)

可得传递函数为

(8)

图3 H(s)的零极点图，为-200～200rad/s

对于条件二，波波夫超稳定性的推导各文献中都有介绍，在此不再赘述。由波波夫超稳定性可以构建自适应律：

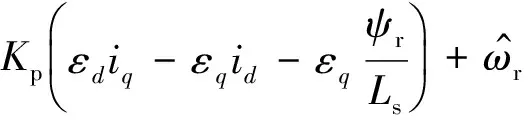
(9)

2 速度观测器中PI参数调节

前文构建了观测器的自适应律即式(9)，那么将式(9)代入图2中的自适应律，即可得图4所示的MRAS结构框图。

图4 MRAS结构图

2.1 系统的传递函数

将图4中虚线部分用状态空间表达式表示：

促进天津市文化产业发展财税政策研 究 ………………………………………… 林永春，黄丽艳，李 慧（65）

(10)

可得其传递函数为

(11)

其和式(8)有着相同的零极点分布。

2.2 有参数的根轨迹分析

将图4进一步简化为图5。

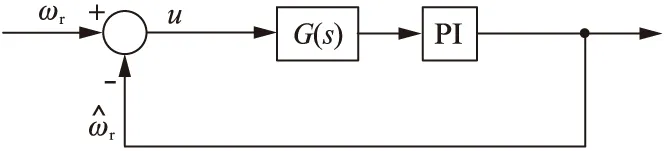
图5 MRAS简化结构图

针对图4的简化结构图用根轨迹分析法来调节PI调节器的参数，使系统达到预期的效果。由于式(11)中id和iq的值比较小，因此可以忽略不计。这样可以得出系统的开环传递函数：

(12)

事实上，由自控原理可得，一般系统的ξ取0.707，因此可以从图6中确定z的范围，使其存在ξ为0.707的系统闭环极点。在图6所示的根轨迹簇下，由于z的增加，根轨迹向外扩展，因此

图6 不同z值下的根轨迹

可以找出能与ξ为0.707这条直线相切的根轨迹。这样就可以确定z的最小值，即只要z大于该值，那么其根轨迹就有ξ为0.707的闭环极点。经过测试，可以得出z≥670。

然后，找出ξ为0.707的2个闭环极点(虚部对称)，k*为开环增益，根据根轨迹，只要能知道某一闭环极点，那么便可得出该极点下开环增益，从而可以确定k*的值，再根据k*的值来找出另一个负实极点。通过测试，得出表1。

表1 不同z值下的闭环极点(ξ=0.707)

最后，根据以上数据可以得出系统的阶跃响应，如图7所示。从而找出满足系统性能的数据来确定PI调节器的参数。

图7 表1数据下的系统阶跃响应

从图7中可以看出编号1的数据性能较好，即含虚部极点要在负实极点左边，且他们的横向距离要最大。这样便可确定PI调节器的参数。

图8 编号1参数下不同的系统阶跃响应

3 仿真分析

本文首先在MATLAB/Simulink中搭建PMSM磁场定向控制模型。然后根据式(3)和式(9)搭建可调模型和自适应律，如图9所示。本文仿真所涉及的参数如表2所示。由表1各个编号的值所确定的PI调节器参数如表3所示。

图9 PMSM无速度传感控制框图

Udc/VPWM周期/kHzLs/mHRs/Ωψr/(V·s)31058．52．87580．175

表3 PI调节器参数

这样，可以得到仿真结果，如图10所示。从图10中可以看出在编号1参数的情况下，观测器的速度响应有着较好的动态性能。在给定转速突变100rad/s时，观测器依然有较好的响应。

图10 转速的仿真结果

4 结 语

针对基于MRAS的PMSM速度观测器中PI调节器参数调节问题，首先以定子电流d、q轴方程建立可调模型，然后根据波波夫超稳定性定理构建自适应律，再用现代控制理论的知识推导观测器的传递函数，最后由根轨迹分析法来找出使得系统有良好动态性能的参数。这种方法可根据电机参数快速地定位出PI调节器的参数，为PMSM无传感器控制提供了理论基础。通过观测器系统的阶跃响应及整个系统的速度响应可看出这种方法的有效性和可行性。具体可得如下结论：

(1) 针对观测器系统的根轨迹，找出ξ为0.707 的含虚部极点。同时根据此时的根轨迹增益找出另一个负实极点。

(2) 含虚部极点要在负实极点左边，并且横向距离要最大。

[1] 禹继贤，颜钢锋，张斌.基于MRAS的永磁同步电机无传感器控制[J].机电工程，2015，32(9)： 1222-1228.

[2] 杜永栋，滕青芳，左瑜君.永磁同步电机的变结构MRAS转速辨识系统[J].自动化仪表，2014，35(12)： 79-82.

[3] 杨宗军，王莉娜.表贴式永磁同步电机的多参数在线辨识[J].电工技术学报，2014，29(3)： 111-118.

[4] 郭兴.基于改进型MRAS的永磁同步电机的转子速度辨识研究[D].长沙： 湖南大学，2013.

[5] 张海燕，刘军，兖涛，等.永磁同步电机在全速范围内的无位置传感器矢量控制[J].电机与控制应用，2014，41(7)： 1-4.

[6] 齐放，邓智泉，仇志坚，等.一种永磁同步电机无速度传感器的矢量控制[J].电工技术学报，2007，22(10)： 30-34.

[7] 王庆龙，张兴，张崇巍.永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J].中国电机工程学报，2014，34(6)： 897-902.

[8] LINDITA D， AIDA S. Simulation based analysis of two different control strategies for PMSM[J]. International Journal of Engineering Trends and Technology， 2013，4(4)： 596-602.

[9] QU Z Y， YE Z M. Speed regulation of a permanent magnet synchronous motor via model reference adaptive control[J]. Advanced Materials Research， 2011，268-270： 513-516.

[10] BOZE Z， YI R. The research on permanent magnetic synchronous motor vector control based on MRAS[J]. Applied Mechanics and Materials， 2015(719-720)： 381-387.

[11] FAN S， LUO W， ZOU J， et al. A hybrid speed sensorless control strategy for PMSM based on MRAS and fuzzy control[C]∥Power Electronics and Motion Control Conference， Harbin， China： IEEE，2012： 2976-2980.

[12] PRADEEP K， MANDEEP K， SURENDER D. Sensor less speed control of PMSM using SVPWM technique based on MRAS method for various speed and load variations[J]. Lecture Notes in Engineering and Computer Science， 2015，2217(1)： 375-380.

[13] MAJID K， GHPHRAN T. Study and comparison the performance of sensorless control of PMSM drive system[J]. Engineering & Technology Journal， 2014，32(10)： 2528-2547.

[14] 张洪帅，王平，韩邦成.基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J].中国电机工程学报，2014，32(12)： 1889-1896.

[15] GAO W， GUO I R. Speed sensorless control of PMSM using model reference adaptive system and RBFN[J]. Journal of Networks，2013，8(1)： 213-220.

[16] LIU K， ZHANG Q， ZHU Z， et al. Comparison of two novel MRAS based strategies for identifying parameters in permanent magnet synchronous motors[J]. International Journal of Automation and Computing，2010，7(4)： 516-524.

[17] YANG J G， ZHOU F， LI B I. Study on sensorless control model based on a model reference adaptive system with parameter optimization[J]. Applied Mechanics and Materials，2011(121-126)： 4770-4778.

[18] KHLAIEF A， BOUSSAK M， CHARI A. A MRAS-based stator resistance and speed estimation for sensorless vector controlled IPMSM drive[J]. Electric Power Systems Research， 2014，108(3)： 1-15.

[19] 邱腾飞，温旭辉，赵峰，等.永磁同步电机永磁磁链自适应观测器设计方法[J].中国电机工程学报，2015，35(9)： 2287-2294.

Method of Adjusting PI Parameters for Permanent Magnet Synchronous Motor Speed Observer Based on Model Reference Adaptive*

LIUXiaojun，ZHANGGuangming，MEILei，WANGDeming

(College of Electrical Engineering and Control Science， Nanjing Tech University， Nanjing 210009， China)

In sensor control， permanent magnet synchronous motor need install encoder and hall sensor， this will undoubtedly increase the cost of the system design. So， it is necessary to study on sensorless control. With the development of modern control theory， sensorless technology was also growing development. The control strategy was based on field oriented control， and then a speed observer was designed based on model reference adaptive theory. The stability of the observer using the knowledge of modern control theory was analyzed， and a new method for adjusting the parameters of PI using the knowledge of traditional control theory was analyzed. This method has a strong adaptability and transplantation. Finally， the accuracy and feasibility of this method were verified.

permanent magnet synchronous motor(PMSM)； sensorless control； model reference adaptive system(MRAS)； stability； adjust the parameters

国家自然科学基金资助项目(51277092；51307080)

刘小俊(1992—)，男，硕士研究生，研究方向为永磁同步电机控制。 张广明(1965—)，男，博士后，教授，博导，研究方向为智能控制理论及应用、机电系统综合控制。

TM 341

A

1673-6540(2016)07-0001-06

2015-11-11