Diophantine方程( an-1) ( ( a+1)n-1) = x2的可解性
2016-04-12裴元太付瑞琴
杨 海,裴元太,付瑞琴
( 1.西安工程大学理学院,陕西西安710048; 2.西安石油大学理学院,陕西西安710065)
Diophantine方程( an-1) ( ( a+1)n-1) = x2的可解性
杨海1*,裴元太1,付瑞琴2
( 1.西安工程大学理学院,陕西西安710048; 2.西安石油大学理学院,陕西西安710065)
摘要:设a是大于1的正整数,v2( a)表示2可以整除a的最高次幂.运用初等数论方法研究了方程( an-1) ( ( a+1)n-1) = x2的可解性.证明了当a满足以下3个条件之一时该方程无解( x,n) : ( i) a是偶数,v2( a)是奇数; ( ii) a是偶数,v2( a) = 2; ( iii) a是奇数且a≡5或9( mod 16).同时也证明了至少有5/6的正整数a可使该方程没有适合n>2的解( x,n).
关键词:指数Diophantine方程;可解性;密率
1引言及主要结论
令N是所有正整数的集合.设a是大于1的正整数,ν2( a)表示2可以整除a的最高次幂.2000年,Szalay[1]证明了当a=2时,方程
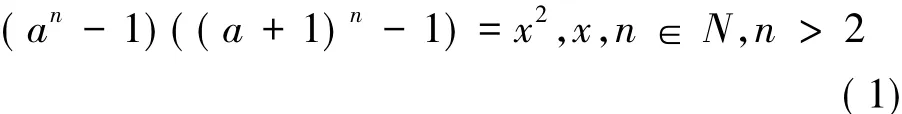
无解( x,n).此后,人们对于方程( 1)及其推广形式进行了很多研究[2-6].最近,梁明[7]证明了当a≡2或3 ( mod 4)时,方程( 1)无解;并且提出猜想:对于任何大于1的正整数a,方程( 1)都无解.这是一个至今尚未解决的问题.由文献[1]的结果可知至少有1/2的正整数a可使方程( 1)无解.
本文运用初等数论方法证明了以下结果:
定理1方程( 1)没有可使n是偶数的解( x,n).
推论1如果正整数a满足下列条件之一,则方程( 1)无解:
( i) a是偶数,ν2( a)是奇数;
( ii) a是偶数,ν2( a) = 2;
( iii) a是奇数,a≡5或9( mod 16).
推论2至少有5/6的正整数a,可使方程( 1)无解( x,n).
显然,上述推论包括了文献[7]在a是偶数时的结果,并且改进了文献[7]中a无解的密率.
2若干引理
引理1[8]对于任何非平方正整数d,方程

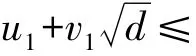

( u,v) = ( uk,vk) ( k=1,2,…)是方程( 2)的全部解.
引理2设( u,v) = ( ur,vr)和( us,vs)是方程( 2)的两组解,其中r,s是不同的正整数.如果2| ur且2 us,那么必有2 r和2|s.
证明情形(Ⅰ) :当2|t时,由式( 3)可知
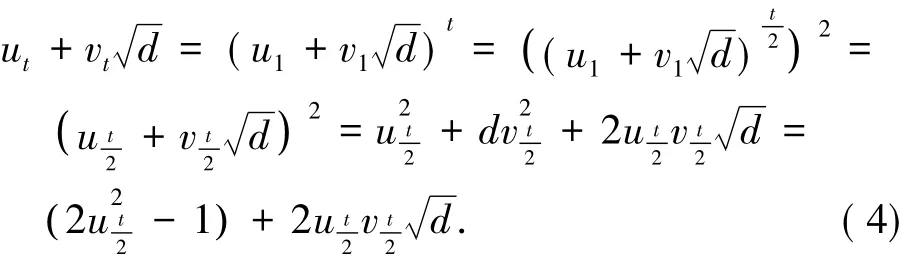
由式( 4)可知此时ut= 2u2
2r-1是奇数.由此可知:如果2|ur,那么

由式( 3)和( 5)可得

因为由式( 2)可知u21-dv21= 1,于是u21和dv21的奇偶性不相同,所以有
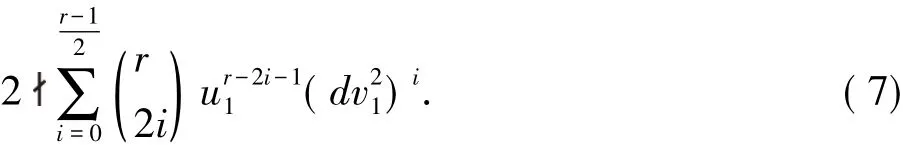
因为2|ur,所以由式( 6)和( 7)可知2 | u1.
情形(Ⅱ) :当2 s时,由式( 6)可知u1|us,故根据2|u1可得2|us.由此可知:如果2 us,那么必有2 | s.于是,由式( 5)和2|s即得本引理.证毕.
引理3[9]方程X2+ 1 = Yn,n>1,X,Y,n∈N无解( X,Y,n).
引理4[10]设p是奇素数,方程Xp+ 1 = 2Y2,min{ X,Y}>1,X,Y∈N仅有解( p,X,Y) = ( 3,23,78).
引理5[3]方程( 1)没有适合4|n的解( x,n).
3定理的证明
设( x,n)是式( 1)的一组n为偶数的解可得

当d=1时,根据引理3可知式( 8)无解,于是d>1为非平方正整数.
如果2 | n,那么由式( 8)中前两个等式可知方程( 2)有两组解

因此,根据引理1和式( 9)可得

当a是偶数时,由式( 10)可知2|ur且2 us,所以根据引理2可得




因为( a+1)2
n
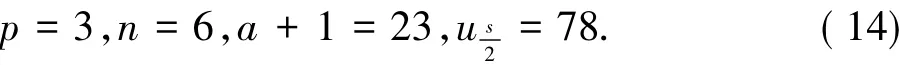
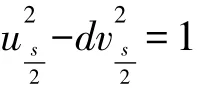

同时,由式( 11)可知2 r,所以由式( 6)可知u1| ur,故由式( 10),( 14)和( 15)可得78|223,矛盾.
同样,当a是奇数时,因为由式( 10)可知2| us且2 ur,所以根据引理2可得

因为2|r,所以由式( 3)和( 10)可得


综上所述可知:方程( 1)没有可使n为偶数的解( x,n).定理证毕.
因此,由式( 18)可得
4推论1的证明
设( x,n)是方程( 1)的一组解,由式( 1)可得式( 8).根据本文定理可知n必为奇数.
情形(Ⅰ) :当a为偶数时,由式( 8)中前2个等式分别可得

由式( 19)可知gcd( a,d) = 1,故由式( 20)可得

当ν2( a)是奇数时,由式( 21)可知2a|z2,故有

因此,由式( 8)中第2个等式和式( 22)可得

由于a是偶数,故由式( 23)可知n也是偶数这一矛盾.因此条件( i)成立.
另外,由式( 8)中前2个等式可得

由式( 24)和( 25)可得
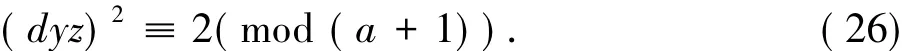
由于此时a+1是奇数,所以根据文献[8]的定理3.6.3和式( 26)可知a+1≡±1( mod 8).由此可得a≡0或6( mod 8).因为当a≡6( mod 8)时,ν2( a) = 1,由条件( i)已知此时方程( 1)无解,故必有

由式( 27)可知:当a≡4( mod 8),即ν2( a) = 2时,方程( 1)也无解.因此条件( ii)成立.

5推论2的证明
对于正整数X,设A( X)是不大于X且使方程( 1)无解的正整数a的个数.对于正整数m,设集合
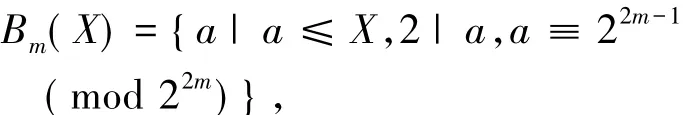
可知Bm( X)中元素a都是适合ν2( a) = 2m-1为奇数的偶数,而且Bm( X)中元素的个数

其中[X/22m]是X/22m的整数部分.因此,根据推论1和文献[7]的定理以及式( 28)可知

上式等号右端第一项1/4即由文献[7]中a≡3( mod 4)部分的结论得出.推论2证毕.
参考文献:
[1]SZALAY L.On the diophantine equation ( 2n-1) ( 3n-1) = x2[J].Publ Math Debrecen,2000,57( 1/2) : 1-9.
[2]HAJDU L,SZALAY L.On the diophantine equation ( 2n-1) ( 6n-1) = x2and ( an-1) ( akn-1) = x2[J].Period Math Hungar,2000,40( 2) : 141-145.
[3]COHN J H E.The diophantine equation ( an-1) ( bn-1) = x2[J].Period Math Hungar,2002,44( 2) : 169-175.
[4]LE M H.A note on the exponential diophantine equation ( an-1) ( bn-1) = x2[J].Publ Math Debrecen,2009,74( 3/4) : 401-403.
[5]LI L,SZALAY L.On the exponential diophantine equation ( an-1) ( bn-1) = x2[J].Publ Math Debrecen,2010,77( 3/ 4) : 465-470.
[6]YUAN P Z,ZHANG Z F.On the diophantine equation ( an-1) ( bn-1) = x2[J].Publ Math Debrecen,2012,80( 3/4) : 327-331.
[7]梁明.关于Diophantine方程( an-1) ( ( a+1)n-1) = x2[J].数学杂志,2012,32( 3) : 511-514.
[8]华罗庚.数论导引[M].北京:科学出版社,1979: 287-289.
[9]LEBESGUE V A.Sur l'impossiblilité en nombres entiers de l'équation xm= y2+ 1[J].Nouv Ann Math,1850,9( 1) : 178-181.
[10]BENNETT M A,SKINNER C M.Ternary diophantine equation via Galois representations and modular forms[J].Canada J Math,2004,56( 1) : 23-54.
The Diophantine Equation ( an-1) ( ( a+1)n-1) = x2
YANG Hai1*,PEI Yuantai1,FU Ruiqin2
( 1.School of Science,Xi'an Polytechnic University,Xi'an 710048,China; 2.School of Science,Xi'an Shiyou University,Xi'an 710065,China)
Abstract:Let a be a positive integer with a>1,and v2( a) denotes the highest power of 2 dividing a.The main purpose of this paper is using elementary number theory methods to study the solvability of the equation ( an-1) ( ( a+1)n-1) = x2.We prove that no solution ( x,n) to the equation exists if one of the following conditions is satisfied: ( i) a is even,and v2( a) is odd; ( ii) a is even,and v2( a) = 2; ( iii) a is odd,and a≡5 or 9 ( mod 16).We also prove that there are at least five sixths of positive integers a which make the equation have no solution ( x,n) with n>2.
Key words:exponential Diophantine equation; solvability; density
*通信作者:xpuyhai@ 163.com
基金项目:国家自然科学基金( 11226038,11371012) ;陕西省教育厅科研计划项目( 14Jk1311)
收稿日期:2015-03-02录用日期: 2015-05-05
doi:10.6043/j.issn.0438-0479.2016.01.017
中图分类号:O 156.7
文献标志码:A
文章编号:0438-0479( 2016) 01-0091-03
引文格式:杨海,裴元太,付瑞琴.Diophantine方程( an-1) ( ( a+1)n-1) = x2的可解性[J].厦门大学学报(自然科学版),2016,55( 1) : 91-93.
Citation: YANG H,PEI Y T,FU R Q.The Diophantine equation ( an-1) ( ( a+1)n-1) = x2[J].Journal of Xiamen University( Natural Science),2016,55( 1) : 91-93.( in Chinese)
