基于季风提高空间相关性预测的优化延迟时间

杨正瓴，杨 钊，张 玺，朱新山，张 军



基于季风提高空间相关性预测的优化延迟时间

杨正瓴1,2，杨 钊1，张 玺1，朱新山1,2，张 军1,2

(1.天津大学电气与自动化工程学院，天津 300072；2.天津市过程检测与控制重点实验室，天津 300072)

由于只依据本地数值天气预报和历史数据的风电功率预测大体进入相对饱和时期，所以依据周边地区风速和风向的空间相关性预测就成为今后提高风速预测效果的主要方法。我国三分之二的国土面积，陆地风能资源丰富区中的沿海和北部的部分区域，以及主要能源消费区都处在季风区，因此利用季风改进空间相关性预测就成为重要的研究课题。季风区不同地点风速时间序列之间，存在显著的延迟相似性。利用相关系数、互信息等可以提取这些优化的延迟时间，并依此实现风速的空间相关性预测。在季风时期，福建长江澳对广东湛江的优化延迟时间约为20 h，明显超过欧美典型的4 h。

季风；空间相关性；风速；预测；延迟时间

0 引言

准确可靠的风电功率预测、大规模储能、电力系统运行实时调度和控制管理等，都是解决电网的风电消纳和弃风的核心技术[1-5]。风电功率预测的主流方法之一是先预测风速风向，再通过风电机组的风速功率曲线，得出未来的风电功率预测值。目前实用的风速风向预测系统，一般都将物理方法和统计学方法结合使用[6-16]。物理方法中的数值天气预报(Numerical Weather Prediction, NWP)是未来的主流方法。统计学方法通常采用各类回归技术，依据风速、风电出力等历史数据来预测未来。由于风速在数小时(如6 h)以后就和当前以及历史风速失去明显的相关性，统计学方法一般对超短期风电预测效果较好，而对12 h之后的预测就较差了[7-11]。

经过国际社会的努力，综合使用物理和统计学方法的风电预测技术，已经开始进入性能提高的相对饱和时期，即这类方法很难再快速地提高预测的效果。因此，空间相关性预测[1,9-16]就成为当前提高风电预测效果的主要方法。在风能资源丰富区，用于风力发电的风系往往具有数百千米以上的空间尺度，因此利用周围其他地点的风速风向等信息，可以提高本地未来的预测效果。这就是空间相关性预测的基本特征。叶林等的文献[1]里有空间相关性预测的定义、概念和基本特点以及实现方法和最新国内外进展，是一篇完整的综述文献。

空间相关性用于风电预测，以希腊学者Minas C. Alexiadis等1998年的文献[13]为早期的代表。他们利用ANN实现了提前1 h风速和风电功率预测。德国的Ulrich Focken等，在2002年报道了利用空间相关性降低未来48 h风电预测误差的研究结果。以德国的风电为例，他们发现利用直径370 km的风场的总预测误差，比单一机组的预测误差降低了63%[14]。综述文献[1]、文献[9-10]里介绍了空间相关性预测的历史，2011年西班牙Sergio Velázqueza等利用多层感知器MLP网络的预测，是文献[9]里最新的报道。这期间使用过测量-相关-预测(Measure- Correlate-Predict)、层次贝叶斯模型、各类人工神经网络等方法，并以周边的历史数据或NWP未来的预测数据作为本地预测的输入。其后2012年澳大利亚Muhammad Khalid等用线性回归实现附近的历史观测和NWP未来预测的结合[15]。依据空间和时间相关性，2014年英国的Jethro Dowell等用循环维纳滤波器实现了对未来风速风向的预测[16]。采用空间相关性预测的各种研究，都提高了预测的准确率和可靠性。研究表明，由于欧美地区风的性质(没有典型的季风现象)，其利用空间相关性一般可以改善未来4 h以内的预测。

空间相关性预测在我国季风区可望取得明显超过欧美的效果[12]。季风是一种大范围盛行的、风向有明显季节变化的风系。我国季风出现时间年均约7个月以上[17]。我国国土面积大约2/3处在季风区，我国主要能源消费区都处在季风区。且我国风能资源丰富区都与季风有关。利用季风的风向稳定性及其风速在地理空间长距离的延迟相似性，可以明显提高空间相关性预测的效果。我国季风区不同地点风速相似的程度、这些相似风速之间的延迟时间以及利用季风提高空间相关性预测准确率的程度，是本文的研究重点。

1 季风区不同地点风速之间的延迟相似性

季风的定义和基本特征，世界季风分布、我国季风区以及我国冬季风、夏季风风向；我国季风区与胡焕庸线，和主要能源消费区之间的示意图，请看文献[12]。下面将以我国福建长江澳(东经119°46′，北纬25°36′)、福建澳仔(东经117°25′，北纬23°36′)、广东湛江(东经110°38′，北纬20°55′)三地某年1 h统计间隔的风速为例，从直观对照、小波分析、相关系数、互信息角度，示例我国季风区不同地点季风之间的延迟相似性：延迟时间，相似性程度。

1.1 长江澳、澳仔和湛江风速时间序列的直观观察与小波分析

图1(a)是全年8 760点的1 h统计间隔的风速时间序列，图1(b)是一个月的典型冬季风。从上到下依次为长江澳50 m高度、澳仔40 m高度和湛江20 m高度的风速。从图1(a)可以直观看出，在典型的冬季风(一般在12月1日~次年2月20日)、夏季风(一般在6月10日~8月20日)期间，三地风速有较明显的延迟相似性。图1(b)是典型冬季风一个月的细节。

图1 长江澳、澳仔和湛江的风速时间序列

我国冬季风、夏季风是两种不同性质的风。长江澳、澳仔和湛江冬季风规律性强，来自海洋的夏季风规律性低。从长江澳50 m高度和湛江20 m高度的风速时间序列的小波周期图、交叉小波图、小波相关图中可以明显看出来。请看图2。

图2 长江澳、湛江风速的小波周期图、交叉小波图、小波相关图

1.2 相关系数

图3为长江澳50 m高度和湛江20 m高度的风速时间序列之间的最大相关系数和延迟时间(单位：小时)。选取一段长江澳风速序列作为基准，用相同长度的湛江风速进行±60 h的前后移位匹配，记录其中最大的相关系数和对应的移位时间(延迟时间)。相关系数置信区间的计算，采用文献[18]的分段函数。

图3 长江澳、湛江风速最大相关系数和对应延迟时间

从图3可见，冬季风从长江澳刮到湛江，大约需要20 h左右的时间。引起冬季风的蒙古高压，是北半球最强的高气压，影响范围可达整个欧亚大陆。因此冬季风风速高、规律性强。春天季风过渡时期(常在3月15日~4月20日)，秋天季风过渡时期(常在9月1日~10月1日)，季风现象消失，两地风速之间的相关性明显比冬季风时期下降。夏季风时期的相似性有一定的提高。典型的冬季风、夏季风和过渡时期的统计，请看表1。本文的“冬季风1”指年初的冬季风，“冬季风2”指年末的冬季风。表1里，季风过渡时期的相关性较低，因此没有找到优化的延迟时间。-60表示到达匹配的边界。

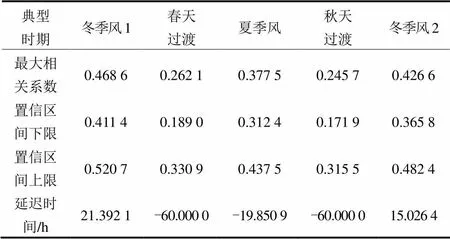
表1 长江澳和湛江之间典型时期的最大相关系数和对应的延迟时间统计

1.3 互信息

图4为长江澳50 m高度和湛江20 m高度的风速时间序列之间的最大互信息和延迟时间(单位：小时)。计算的流程同前面的相关系数。计算互信息的程序，参见文献[19]的有关说明。

图4 长江澳、湛江风速最大互信息和对应延迟时间

图4的互信息计算结果，大体证实了前面小波、相关系数的分析结果。由于互信息直接反映风速之间的概率密度关系，而不直接反映风速本身，因此互信息的判断效果不如小波、相关系数这些直接反映风速本身信息的方法。

典型的冬季风、夏季风和过渡时期的互信息和延迟时间统计，请看表2。类似表1，春秋季风过渡时期的互信息，仅为参考值。

表2 长江澳和湛江之间典型时期的最大互信息和对应的延迟时间统计

采用相同分析表明，福建澳仔对广东湛江的季风时期优化延迟时间约为14 h。相关性强度高于长江澳。

2 湛江风速预测示例

在非平稳时间序列分析与预测中，由于线性方法具有超过非线性方法的可靠性和稳健性[20]，所以本文采用线性方法来进行湛江风速提前1 h的预测。

2.1 线性自回归预测

采用6阶线性自回归AR(6)进行预测，进行提前1 h的滚动预测。表3是预测误差的统计，单位为m/s。预测的方程为

表3 湛江风速时间序列AR(6)提前1 h 滚动预测的误差统计

2.2 空间相关性预测

采用长江澳50 m、澳仔40 m历史风速来滚动预测湛江20 m高度的提前1 h风速，即

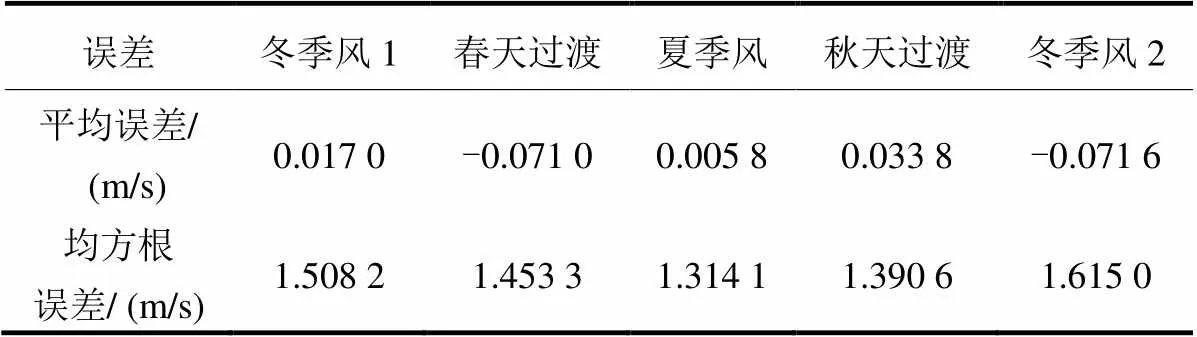
表4 采用空间相关性的湛江风速时间序列提前1 h滚动预测的误差统计

对照表3可见：在季风区，空间相关性预测可以取得有实际意义的预测效果。可以实现提前20 h左右的预测，明显超过欧美4 h的典型水平。对照气象局的NWP预测，季风区的空间相关性预测对冬季风爆发引起的爬坡更有积极意义。

实际上，还可用长江澳50 m、澳仔40 m高度风速的NWP等预测值，来回归出湛江未来的风速，通过组合预测等方法进一步提高预测的效果。

2.3 示例结果与风电爬坡预测

上述示例表明，采用空间相关性可以进行数小时以上的未来风速预测。这本身也隐含了对快速的较大幅度的季风风速变化引起的风电功率爬坡事件的预测。

由于大气在天气过程中可看作不可压缩流体，实际中常见情况下的季风风速上升或下降速率与风速数值的关系并不很明显。因此，利用空间相关性，可以有效地进行爬坡事件的预报和预警。地面附近的风向，略平行于等大气压线偏向低压区。这是因为风主要受三种力的影响：气压梯度力，科里奥利力(Coriolis force，地球自转引起)以及地形起伏等引起的摩擦力(下垫面)。因此，季风上游各地的风速、风向、气压(位势高度)是实用的空间相关性预测的输入变量。目前的NWP预测风速与大气中实际风速的较长时间区间(如3 h)的平均风速有明显的关系，而对快速的风速变化(如1 h以内)的预报效果较不准确。因此，空间相关性对风电功率爬坡，特别是季风时期的爬坡，有目前其他方法无法替代的优点。

我国季风现象的平均移动速度大约在50 km/h的水平，因此建议按照季风路径，每隔30~50 km建立一个100 m高度的测风塔，以便及时可靠地捕捉到季风的行为。利用这种连续性的季风观测，可以有效地发现季风的大幅度快速变化，并通过空间相关性进行可靠的预测。亦即利用季风特性的空间相关性，可以对爬坡事件进行较为准确可靠的预测和预警。

3 结论

(1) 季风是我国特有的有利自然条件。利用季风的空间相关性预测，可以实现明显超过欧美的提前预测时间。

(2) 通过相关系数、互信息等，可以求出优化的延迟时间。依据这些优化的延迟时间，将长江澳、澳仔风速作为输入，通过线性回归可以预报湛江风速，取得有意义的预测结果。

未来的研究目标，是建立多地之间互为因果的空间相关性预测网络，大范围地联合提高风电功率的预测效果。

[1] 叶林, 赵永宁. 基于空间相关性的风电功率预测研究综述[J]. 电力系统自动化, 2014, 38(14): 126-135.

YE Lin, ZHAO Yongning. A review on wind power prediction based on spatial correlation approach[J]. Automation of Electric Power Systems, 2014, 38(14): 126-135.

[2] 刘畅, 吴浩, 高长征, 等. 风电消纳能力分析方法的研究[J]. 电力系统保护与控制, 2014, 42(4): 61-66.

LIU Chang, WU Hao, GAO Changzheng, et al. Study on analysis method of accommodated capacity for wind power[J]. Power System Protection and Control, 2014, 42(4): 61-66.

[3] 薛禹胜, 郁琛, 赵俊华, 等. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化, 2015, 39(6): 141-151.

XUE Yusheng, YU Chen, ZHAO Junhua, et al. A review on short-term and ultra-short-term wind power prediction[J]. Automation of Electric Power Systems, 2015, 39(6): 141-151.

[4] 张新松, 礼晓飞, 王运, 等. 不确定性环境下考虑弃风的电力系统日前调度[J]. 电力系统保护与控制, 2015, 43(24): 75-82.

ZHANG Xinsong, LI Xiaofei, WANG Yun, et al. Day-ahead dispatching in consideration of wind power curtailments in uncertain environments[J]. Power System Protection and Control, 2015, 43(24): 75-82.

[5] 朱倩雯, 叶林, 赵永宁, 等. 风电场输出功率异常数据识别与重构方法研究[J]. 电力系统保护与控制, 2015, 43(3): 38-45.

ZHU Qianwen, YE Lin, ZHAO Yongning, et al. Methods for elimination and reconstruction of abnormal power data in wind farms[J]. Power System Protection and Control, 2015, 43(2): 38-45.

[6] 刘立阳, 吴军基, 孟绍良. 短期风电功率预测误差分布研究[J]. 电力系统保护与控制, 2013, 41(12): 65-70.

LIU Liyang, WU Junji, MENG Shaoliang. Research on error distribution of short-term wind power prediction[J]. Power System Protection and Control, 2013, 41(12): 65-70.

[7] WANG J Z, WANG Y, JIANG P. The study and application of a novel hybrid forecasting model - a case study of wind speed forecasting in China[J]. Applied Energy, 2015, 143: 472-488.

[8] 刘爱国, 薛云涛, 胡江鹭, 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制, 2015, 43(2): 90-95.

LIU Aiguo, XUE Yuntao, HU Jianglu, et al. Ultra-short- term wind power forecasting based on SVM optimized by GA[J]. Power System Protection and Control, 2015, 43(2): 90-95.

[9] JUNG J, BROADWATER R P. Current status and future advances for wind speed and power forecasting[J]. Renewable and Sustainable Energy Reviews, 2014, 31: 762-777.

[10] MA L, LUAN S Y, JIANG C W, et al. A review on the forecasting of wind speed and generated power[J]. Renewable and Sustainable Energy Reviews, 2009, 13(4): 915-920.

[11] 简金宝, 刘思东. 风速空间相关性和最优风电分配[J]. 电力系统保护与控制, 2013, 41(19): 110-117.

JIAN Jinbao, LIU Sidong. Wind speed spatial correlation and optimal wind power allocation[J]. Power System Protection and Control, 2013, 41(19): 110-117.

[12] 杨正瓴, 冯勇, 熊定方, 等. 基于季风特性改进风电功率预测的研究展望[J]. 智能电网, 2015, 3(1): 1-7.

YANG Zhengling, FENG Yong, XIONG Dingfang, et al. Research prospects of improvement in wind power forecasting based on characteristics of monsoons[J]. Smart Grid, 2015, 3(1): 1-7.

[13] ALEXIADIS M C, DOKOPOULOS P S, SAHSAMANOGLOU H S, et al. Short-term forecasting of wind speed and related electrical power[J]. Solar Energy, 1998, 63(1): 61-68.

[14] FOCKEN U, LANGE M, MONNICH K, et al. Short-term prediction of the aggregated power output of wind farms-a statistical analysis of the reduction of the prediction error by spatial smoothing effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(3): 231-246.

[15] KHALID M, SAVKIN A V. Closure to discussion on “a method for short-term wind power prediction with multiple observation points”[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1898-1899.

[16] DOWELL J, WEISS S, HILL D. Short-term spatio- temporal prediction of wind speed and direction[J]. Wind Energy, 2014, 17(12): 1945-1955.

[17] WANG B. The Asian monsoon[M]. New York: Springer- Verlag, 2006.

[18] YANG Zhengling, DUAN Zhifeng, WANG Jingjing, et al. Quadratic radical function better than fisher z transformation[J]. Transactions of Tianjin University, 2013, 19(5): 381-384.

[19]YANG Zhengling, FENG Yong, XIONG Dingfang, et al. Analytical fitting functions of finite sample discrete entropies of white Gaussian noise[J]. Transactions of Tianjin University, 2015, 21(4): 299-303.

[20] FAN J Q, YAO Q W. Nonlinear time series: nonparametric and parametric methods[M]. New York: Springer-Verlag, 2003.

(编辑 魏小丽)

Improving optimal lag time of spatial correlation prediction by characteristics of monsoon

YANG Zhengling1, 2, YANG Zhao1, ZHANG Xi1, ZHU Xinshan1, 2, ZHANG Jun1, 2

(1. School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China; 2. Key Laboratory of Process Measurement and Control, Tianjin 300072, China)

Since the prediction of wind power only by local NWP and historical observations has saturated, the spatial correlation approaches, which employ the wind speeds and directions of surrounding areas, become the main methods to improve the prediction of wind speed in the future. To improve the spatial correlation prediction by characteristics of monsoon is very important for China, because the 2/3 area, the littoral and northern part of wind energy resources rich areas as well as the major energy consumption areas of China are all located in monsoon regions. The wind speed time series between different places are obviously similar after some lag time. The optimal lag time can be calculated by the correlation coefficient and mutual information, which can improve the spatial correlation prediction. In the monsoon durations, the optimal lag time of wind speed from Changjiangao to Zhanjiang is about 20 hours, which is significantly larger than the typical 4 hours in Europe and America.

monsoon; spatial correlation; wind speed; prediction; lag time

10.7667/PSPC151551

杨正瓴(1964-)，男，博士，副教授，研究方向为电力负荷、风电功率预测；E-mail: zlyang@tju.edu.cn 杨 钊(1990-)，男，硕士研究生，研究方向为风电功率预测；E-mail: yangzhaofield@126.com 张 玺(1987-)，男，硕士研究生，研究方向为风电功率预测。E-mail: zhangxi_1220@126.com