人体二尖瓣瓣膜厚度有限元分析及其仿真

王 聪,黄晓阳*,苏茂龙(1.福建省智慧城市感知与计算重点实验室(厦门大学),2.厦门大学信息科学与技术学院,福建厦门61005;.厦门市心血管病医院,福建厦门61004)



人体二尖瓣瓣膜厚度有限元分析及其仿真

王 聪1,2,黄晓阳1,2*,苏茂龙3
(1.福建省智慧城市感知与计算重点实验室(厦门大学),2.厦门大学信息科学与技术学院,
福建厦门361005;3.厦门市心血管病医院,福建厦门361004)

摘要:建立了基于亚区结构的人体二尖瓣模型,对二尖瓣从开放到闭合的整个过程进行仿真,分析心动周期过程中二尖瓣前后叶的应力分布差异,证实该有限元模型与实际生理相符.在该模型的基础上建立11个具有不同瓣膜厚度的比对模型,对比不同瓣膜厚度下二尖瓣的应力分布情况,分析瓣膜厚度对二尖瓣闭合程度的影响.实验结果表明随着二尖瓣瓣膜厚度增加,其整体应力水平虽然下降,但影响了二尖瓣性能的正常发挥,加重了二尖瓣关闭不全,同临床实际生理情况相吻合.实验结果验证了二尖瓣瓣膜厚度对二尖瓣应力分布具有较大影响,为更深入的研究和了解二尖瓣工作机制奠定了基础.

关键词:二尖瓣;有限元分析;瓣膜厚度;应力分布

二尖瓣是人体心脏中左心室、左心房间的瓣膜组织,可保障心脏中血液的单向流动.二尖瓣的瓣叶分为前后叶,临床上将2个瓣叶各自划分为3个亚区.在研究中,通常将前叶看作一个完整的瓣尖,后叶则细化为3个较窄的瓣尖[1].在腱索的作用下,乳头肌牵拉二尖瓣前后叶完成瓣叶的开放与闭合[2].在心脏收缩期,两片瓣叶的边缘闭合;心脏舒张期,两片瓣叶开放,血液单向流动.

为了有效地评估二尖瓣病变情况,首先需要了解正常二尖瓣的工作原理.通过建立有限元模型并进行仿真,可达到定量测量压力等力学数据的目标,是目前较好的研究方法.对正常及病变二尖瓣进行有限元仿真,模拟二尖瓣不同时相的受力情况,对于研究二尖瓣关闭不全等心脏疾病具有重要意义.

目前很多学者已经对人体二尖瓣进行了建模仿真,且已经取得了一些进展:罗云等[3]仿真了长方形无支架心包二尖瓣;Kunzelman等[4]仿真了正常及病态的二尖瓣运动状态;Lau团队[5]建立了流固耦合的二尖瓣模型,但该模型多处与临床上的二尖瓣结构不一致;Prot等[6]模拟了肥厚型梗阻性心肌病患者的二尖瓣瓣叶运动状态;罗云等[7]成功模拟二尖瓣闭合状态,但其未考虑二尖瓣前后叶的亚区结构;钟琪等[8]在模型细化的基础上研究了二尖瓣的受力情况及腱索的作用;赵晓佳等[9]在基于亚区的二尖瓣模型基础上,对二尖瓣的厚度设置了均匀与不均匀2种模型进行比对分析,并在此基础上仿真了瓣环与乳头肌的运动.

这些研究均较少涉及二尖瓣瓣膜厚度及对其性能的详细比对分析:罗云[7]虽然分析了二尖瓣厚度的作用,但其模型不够精细,未考虑瓣叶的亚区结构;赵晓佳等[9]在对二尖瓣厚度的分析中,只简单地对比了厚度均匀与厚度不均匀2种情况,并且对二尖瓣腱索属性进行了统一处理,而临床上边缘腱索和其余腱索弹性属性不一致.临床上二尖瓣瓣膜厚度是影响瓣叶性能的主要因素之一,对二尖瓣作用的正常发挥具有决定性意义.研究表明,一定厚度范围内,瓣叶厚度增加,使得瓣膜开启相同等效面积所需要的压力也增大[10],同时二尖瓣厚度与某些疾病的治疗密切相关,如经皮球囊二尖瓣狭窄扩张术(PBMV)的诊断和治疗效果与二尖瓣瓣膜厚度有直接关系[11-12],对瓣叶厚度的研究可以指导临床医生选择二尖瓣球囊扩张手术或者直接进行瓣膜置换手术;在二尖瓣脱垂的研究中瓣叶的厚度也有重要意义[13].瓣膜厚度的不同会影响二尖瓣的应力分布,其厚度的临界值意味着瓣叶僵硬度明显增加,相应腱索牵拉瓣膜的牵拉力也不同,瓣膜应力也会发生变化.实际生理中,风湿性心脏病二尖瓣狭窄,进行二尖瓣球囊扩张手术时必须进行超声心动图学评分,1988年Wilkins等[14]创建了超声心动图学评分系统来评价二尖瓣狭窄是否适合进行二尖瓣球囊扩张手术,该评分系统从瓣叶的4个方面进行超声评分,其中很重要的就是瓣叶厚度.因此细化二尖瓣前后叶,建立符合真实形态的二尖瓣模型,分析瓣膜厚度对应力分布及运动状态的影响,对临床心脏疾病的治疗具有重要意义.

本文以人体二尖瓣真实的生理结构为基础,考虑瓣叶的亚区结构,将后瓣叶划分为3个小的瓣尖,建立了与实际情况接近的物理模型,用有限元方法模拟了心脏收缩初期压力斜坡(early systolic pressure ramp,ESPR)区,二尖瓣的应力分布情况.并在此基础上,建立了不同瓣膜厚度的二尖瓣模型,研究分析瓣膜厚度对二尖瓣应力分布及闭合情况的影响,为后期研究二尖瓣力学机理,疾病诊断和治疗等提供指导.

1 方 法

有限元分析方法是一种高效、常用的计算方法,它是将一个物体或系统分解为多个相互联结的、简单、独立的点组成的几何模型.在求解中,将各个离散单元的关系表达式组合成为含有未知参数的方程组,通过对该方程组的求解,得到相关参数,并利用插值函数得到近似解.其一般步骤分为前处理过程、求解过程以及后处理部分.

本文使用UG(unigraphics NX:交互式CAD/ CAM系统)建立符合二尖瓣解剖结构的物理模型,并利用有限元分析软件(ANSYS)进行前处理.最后使用LS-DYNA进行有限元求解,并通过LS-Prepost查看结果.

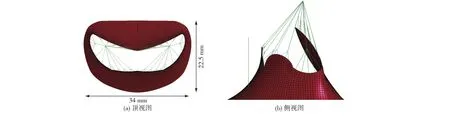
图1　人体二尖瓣几何模型Fig.1 Geometric model of human mitral valve

1.1二尖瓣模型

本文根据文献描述的二尖瓣几何结构[15-16]建立物理模型.由于二尖瓣的对称性,建立一半的结构模型,通过镜面反射得到整体模型(图1).其中,二尖瓣包含以下4个结构.

瓣环与瓣叶:瓣环呈D字形,本模型中前瓣叶为1个瓣尖,后瓣叶分为3个瓣尖.

乳头肌:由于乳头肌在整个心动周期内的位置相对固定,可以假设乳头肌为静态的点.

腱索:本模型中,有10根腱索与前瓣叶相连,14根腱索与后瓣叶相连.从腱索与瓣叶连接位置上划分,边缘腱索与瓣叶的自由边缘相连,其他腱索与瓣叶相连的位置更远,即接近瓣环的位置[17].

1.2材料属性

瓣叶:简化为各向同性材料,且设置瓣叶厚度均匀.各参数设置如表1所示.

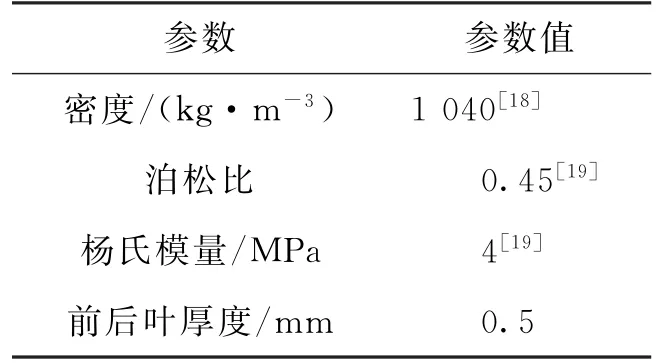
表1　瓣叶属性Tab.1 Property of leaflets

腱索:腱索设置为超弹性材料,根据Kunzelman[17]团队的生理测量数据及实际的生理情况,可将腱索分为两类:边缘腱索与其他腱索.其中,边缘腱索的刚度较大,其余腱索的刚度较小,两类腱索的应力-应变曲线如图2.

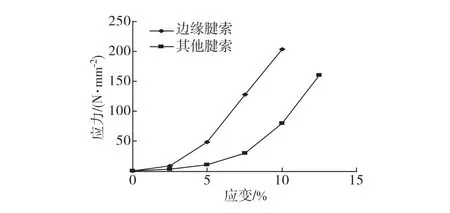
图2　腱索材料应力-应变曲线Fig.2 Stress-strain behavior of mitral valve chordae tendineae

边界与负载:由于二尖瓣的对称性,在对称面的法向量上该面所有节点位移为0.临床上二尖瓣瓣环与乳头肌的位置相对不变,设置其节点位移均为0.心脏ESPR区左心室与左心房的压差数据如表2所示[9].

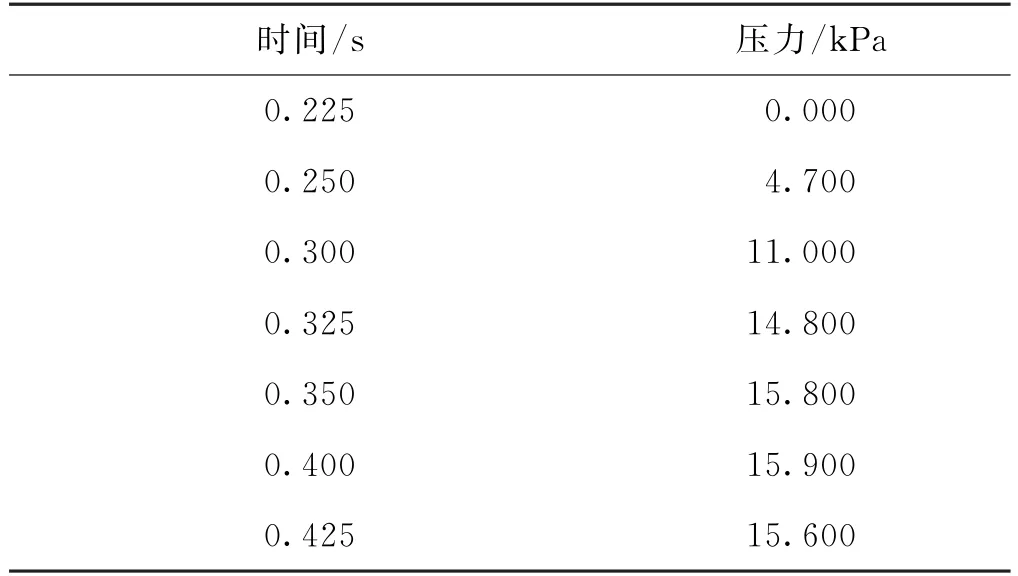
表2　二尖瓣载荷值Tab.2 Transvalvuar pressure load applied to the mitral valve

接触设置:设置瓣膜接触类型为自动单面接触(CONTACT_AUTOMATIC_SINGLE_SURFACE),腱索与瓣叶之间的接触为固连点面接触(CONTACT_ TIED_NODES_TO_SURFACE).

2 结 果

2.1二尖瓣瓣叶应力分布

通过模拟ESPR时期瓣膜的闭合过程,对225, 250,300,325,350,400,425 ms 7个时间点的受力结果进行分析.

实验结果表明,t=225 ms时,二尖瓣左房室压差大约为0,此时瓣叶的整体应力水平较低,集中在2.522 k Pa左右,最大应力约12.6 k Pa,位于腱索与瓣叶连接处;t=250 ms时,瓣叶的应力水平增大,出现应力集中现象,分布在腱索与瓣叶连接位置、瓣叶与瓣环连合处、瓣叶中心位置,最大应力达到0.433 MPa,位于腱索牵拉的瓣叶游离边缘;t=300 ms时,瓣叶的应力集中在0.226～0.452 MPa,最大应力值达到0.753 MPa,位于腱索与瓣叶连接处;t=325 ms 时,最大应力值达到0.899 MPa,位于P2亚区与其他两个亚区的裂口位置;t=350 ms时,瓣膜应力水平继续增大,瓣叶最大应力仍位于P2亚区与P1、P3亚区的裂口位置,达到1.051 MPa;t=400 ms时,二尖瓣整体应力水平较为均匀,集中在0.200～0.620 MPa,最大应力值达到1.044 MPa;t=425 ms时,二尖瓣的整体应力水平几乎不变,集中在0.207～0.621 MPa,最大应力值下降至1.036 MPa,位于亚区间的裂口位置,与临床上容易撕裂的位置一致[20].

此外,本文还分析了前后叶中心区域的受力情况.并与其他学者的模型比较分析,结果如表3.从表3数据可知,本文与其他模型结果基本一致.由于本文建立的模型以亚区结构为特征,细化了前瓣叶,并且根据临床数据将腱索分为两类,所得二尖瓣模型更接近实际生理情况,而结果与与其他模型相符,从而说明模型的有效性.因此可在该模型的基础上比对分析瓣膜的厚度.

表3　不同模型von Mises应力对比Tab.3 Comprison of maximum von Mises stress around the central unit of anterior and posterior of different model

2.2瓣膜厚度与瓣膜应力关系

二尖瓣瓣膜的厚度影响二尖瓣的闭合程度.临床上,瓣叶厚度以4～5 mm为临界值,在厚度大于5 mm时出现二尖瓣严重关闭不全[14];在有限元仿真中,学者们通常将二尖瓣瓣叶厚度设置为0.5～2 mm[4,8,10],其中选取厚度为1 mm左右的最为常见.因此本文选取了0.5～6 mm中11个厚度值,并且在0.5～2 mm区间进行较为细致的厚度对比分析,以此建立11个不同瓣叶厚度的二尖瓣模型,使用有限元分析方法,分析瓣膜厚度对二尖瓣形态以及应力分布的影响.不同瓣叶厚度的二尖瓣模型最终的闭合情况如图3所示.

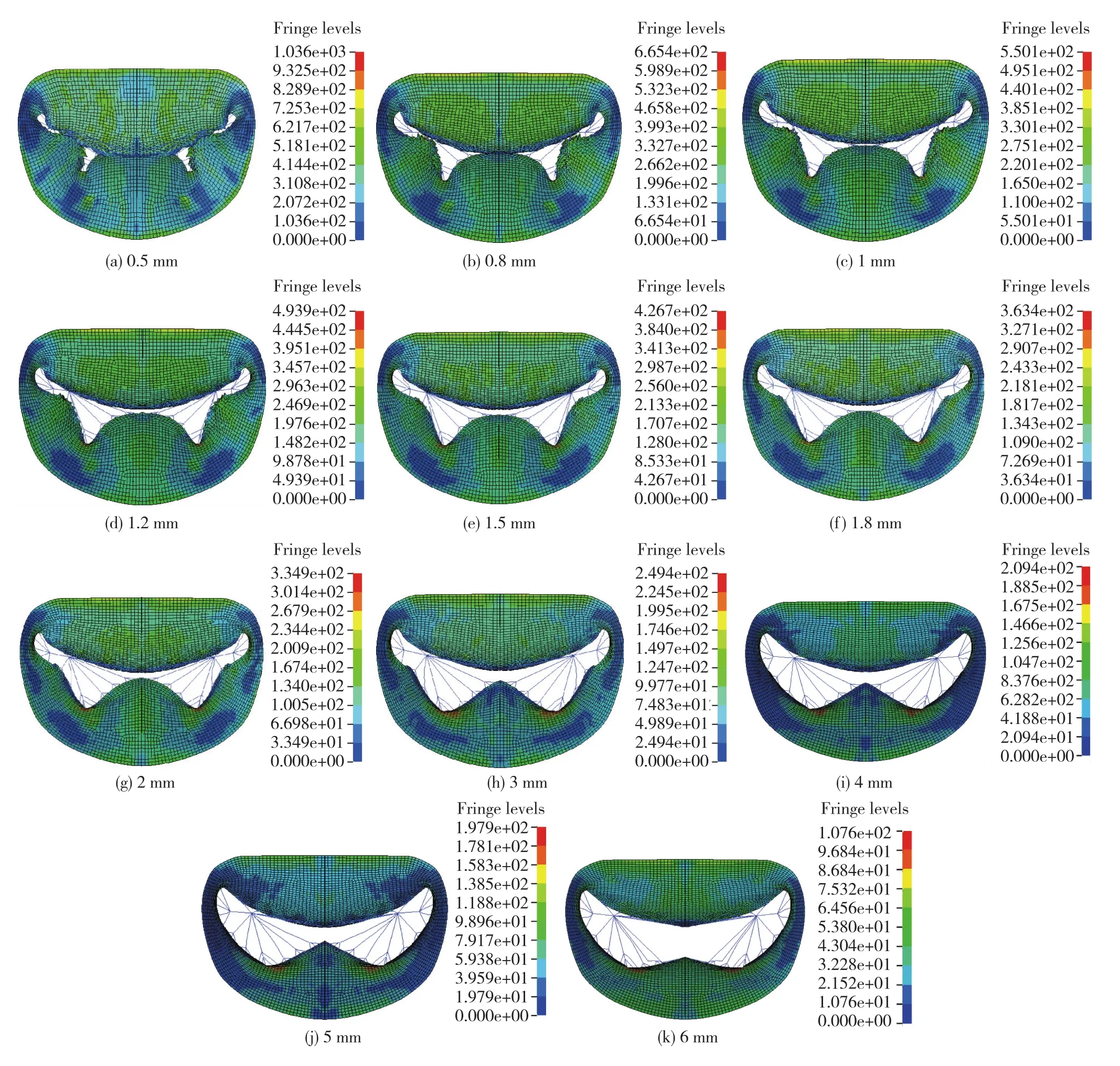
图3　不同瓣膜厚度下二尖瓣模型应力分布对比Fig.3 von Mises stress distribution on the valve leaflets of different thickness

图3表明,随着二尖瓣模型中瓣膜厚度的增加,瓣膜的整体应力水平与最大应力都相应减小.而应力分布集中现象在各不同厚度的二尖瓣模型的ESPR周期中均有出现,应力最大的位置均集中在后瓣叶各亚区相接的裂口位置.当二尖瓣模型瓣膜厚度逐渐增大时候,应力逐渐下降,瓣叶的闭合程度也降低.

由模型在ESPR时期内的最大应力值得出瓣膜厚度对瓣叶最大应力的影响,如图4所示;由其闭合状态得出瓣叶厚度与瓣叶闭合时返流口面积的关系如图5所示.由图4可知:瓣膜厚度越大,其最大von Mises应力值越小,整体有较为均匀的应力分布情况,瓣膜厚度为4～5 mm时趋于稳定,当厚度大于5 mm后应力值减小趋势增大.由图5中瓣叶闭合时返流口情况可知,在瓣膜厚度逐渐增加时二尖瓣关闭不全逐渐加剧,并且在4～5 mm趋于稳定,在瓣膜厚度大于5 mm时关闭不全趋势增大.这与Protd[6]的仿真结果一致.实验结果表明瓣膜厚度的增加会使得整体应力水平下降,但是会加重二尖瓣关闭不全,这与临床上变化趋势相符合;瓣叶厚度以4～5 mm为临界值,这与临床上的区分标准一致,同时在厚度大于5 mm时出现二尖瓣严重关闭不全,这也与临床上病理特征相符[14].而在实际仿真中,结合不同瓣膜厚度下的最大应力与返流口面积,为使二尖瓣受力较小且闭合较为完全,通常将二尖瓣厚度设置为0.5～2 mm,这也与众多研究相符合.其中:钟琪在对腱索研究时将二尖瓣瓣叶厚度设置为0.5 mm[8],在细化瓣叶结构中将二尖瓣前后叶分别设置为1.32,1.26 mm[20-21];同时Kunzelman等[4]在对具有不均匀厚度的二尖瓣模型进行流固耦合的研究中将瓣膜厚度设置在1.000～ 1.690 mm;朱海燕[10]和Pro等[22]对二尖瓣瓣膜厚度的粗略比较中将厚度设置在了0.5～1 mm;赵晓佳等[9]对二尖瓣的研究中将厚度设定为1.3 mm.

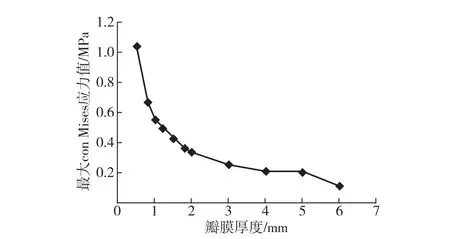
图4 瓣膜最大应力与瓣膜厚度曲线Fig.4 Stress-thickness behavior of mitral valve

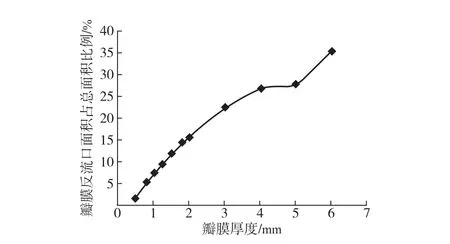
图5 瓣膜返流口面积与瓣膜厚度曲线Fig.5 Regurgitant orifice area-thickness behavior of mitral valve

3 结 论

本文建立了符合真实生理情况的二尖瓣模型,其中腱索分为两类,同时将二尖瓣的后叶细分为3个亚区.对二尖瓣瓣叶施加心房心室压差曲线,仿真二尖瓣在ESPR时期的闭合过程,得到正确有效的二尖瓣模型.鉴于临床上二尖瓣厚度对二尖瓣正常工作的重要性,在此模型的基础上,通过仿真11个不同瓣膜厚度的比对模型,比对各个瓣膜厚度模型下二尖瓣的应力情况及闭合情况,实验结果表明瓣膜厚度的增加会使得整体应力水平下降,但同时加重了二尖瓣关闭不全,这与临床中的变化趋势一致.本文表明仿真中取厚度在0.5～2 mm之间进行研究较为准确,这与实际学者的研究范围相符合;瓣叶厚度4～5 mm为临界值,大于5 mm时即为瓣叶增厚,与临床相符合.

人体二尖瓣的前后叶均可以划分为3个亚区,其厚度也不均匀,这使得二尖瓣受力均匀,不易撕裂.本文模拟的人体二尖瓣模型将前瓣叶看作一个单独的瓣叶,与真实二尖瓣存在一定差异.本文中也没有涉及到血液流体动力学部分,而实际生理情况二尖瓣与血流共同作用,完成心脏的工作职能.后续将会深入研究模型的精细化,并且考虑结构与流体的耦合作用下瓣膜以及血液的运动情况.

参考文献:

[1] DOMINIK J,ZACEK P.Heart valve surgery:an illustrated guide[M].Berlin:Spring-Verlag,2010:10-11.

[2] 黄化清.二尖瓣腱索断裂[J].临床心血管病杂志,1985,1 (1/2):80-83.

[3] 罗云,宋晓,黄晓阳,等.长方形无支架心包二尖瓣的生物力学分析[J].厦门大学学报(自然科学版),2013,52(6): 776-780.

[4] KUNZELMAN K S,EINSTEIN D R,COCHRAN R P. Fluid—structure interaction models of the mitral valve: function in normal and pathological states [J]. Philosophical Transactions of the Royal Society B:Biological Sciences,2007,362(1484):1393-1406.

[5] LAU K D,DIAZ V,SCAMBLER P,et al.Mitral valve dynamics in structural and fluid—structure interaction models[J].Medical Engineering & Physics,2010,32(9): 1057-1064.

[6] PROT V,SKALLERUD B,SOMMER G,et al.On modelling and analysis of healthy and pathological human mitral valves:two case studies[J].Journal of the Mechanical Behavior of Biomedical Materials,2010,3(2):167-177.

[7] 罗云.二尖瓣有限元建模与生物力学分析[D].厦门:厦门大学,2014.

[8] 钟琪,曾文华,黄晓阳,等.人体二尖瓣建模及生物力学分析[J].医用生物力学,2014,29(1):53-59.

[9] 赵晓佳,宋晓,黄晓阳,等.基于亚区结构的人体二尖瓣的建模与仿真[J].厦门大学学报(自然科学版),2015,54 (2):276-280.

[10] 朱海燕.基于ANSYS/LS～DYNA的生物瓣膜动态力学性能分析[D].济南:山东大学,2011.

[11] 孙华保,罗蔚桓.二尖瓣厚度与经皮球囊二尖瓣扩张术疗效的初步探讨[J].实用医学杂志,1996,12(5): 282-283.

[12] 聂娅,姜武.不同原因所致二尖瓣脱垂超声,手术及病理对比分析[J].中国超声医学杂志,1998,14(6):27.

[13] MALEV E,REEVA S,VASINA L,et al. Cardiomyopathy in young adults with classic mitral valve prolapse[J].Cardiology in the Young,2014,24(4): 694-701.

[14] WILKINS G T,WEYMAN A E,ABASCAL V M,et al. Percutaneous balloon dilatation of the mitral valve:an analysis of echocardiographic variables related to outcome and the mechanism of dilatation[J].British Heart Journal,1988,60(4):299-308.

[15] LAM J H,RANGANATHAN N,WIGLE E D,et al. Morphology of the human mitral valve:Ⅰ.Chordae tendinese:a new classification[J].Circulation,1970,41(3): 449-458.

[16] RANGANATHAN N,LAM J H C,WIGLE E D,et al. Morphology of the human mitral valve:Ⅱ.The valve leaflets[J].Circulation,1970,41:459-467.

[17] KUNZELMAN K S,COCHRAN K P.Mechanical properties of basal and marginal mitral valve chordae tendineae[J].ASAIO Trans,1990,36(3):M405-M408.

[18] LAU K D,DIAZ V,SCAMBLER P,et al.Mitral valve dynamics in structural and fluid—structure interaction models[J].Medical Engineering & Physics,2010,32 (9):1057-1064.

[19] PAN F D,DONZELLA G,FUCCI C,et al.Structural effects of an innovative surgical technique to repair heart valve defects[J].J Biomech,2005,38:2460-2471.

[20] 卢晓芳,吕清,谢明星,等.实时三维超声心动图评价二尖瓣裂的初步研究[J].中国医学影像技术,2006,22(4): 490-492.

[21] 钟琪.人体心脏二尖瓣有限元建模与仿真[D].厦门:厦门大学,2014.

[22] PROT V,HAAVERSTAD R,SKALLERUD B.Finite element analysis of the mitral apparatus:annulus shape effect and chordal force distribution[J].Biomechanics and Modeling in Mechanobiology,2009,8(1):43-55.

Simulation and Research on Thicknesses of Human Mitral Valves

WANG Cong1,2,HUANG Xiaoyang1,2*,SU Maolong3
(1.Fujian Key Laboratory of Sensing and Computing for Smart City,Xiamen University,
2.School of Information Science and Engineering,Xiamen University,Xiamen 361005,China; 3.Xiamen Cardiovascular Hospital,Xiamen 361004,China)

Abstract:A model based on the mitral valve sub-region has been established to simulate the process of early systolic pressure ramp. Stress distribution of anterior and posterior and the morphological motion state at different times have been shown.Results show that the finite element model is correct.On the basis of that model,11 models have been developed to compare the stress distribution and closure state under different thicknesses of the mitral valve.With the increasing of thickness,the overall stress decreasesbut the normal functioning mitral valve performance is affected,resulting in the aggravation of mitral regurgitation.The result is consistent with characteristics of the mitral hypertrophy.It further shows that the thickness of mitral valve exerts a great impact on the cardiac process,and lays the foundation for further studies of mitral valve.

Key words:mitral valve;finite element model;mitral valve thickness;stress distribution

*通信作者:xyhuang@xmu.edu.cn

基金项目:国家自然科学基金(61102137,61271336);福建省自然科学基金(2014J01438)

收稿日期:2015-04-21 录用日期:2015-11-26

doi:10.6043/j.issn.0438-0479.2016.02.021

中图分类号:TP 391

文献标志码:A

文章编号:0438-0479(2016)02-0272-06

引文格式:王聪,黄晓阳,苏茂龙.人体二尖瓣瓣膜厚度有限元分析及其仿真[J].厦门大学学报(自然科学版),2016,55(2): 272-277.

Citation:WANG C,HUANG X Y,SU M L.Simulation and research on thicknesses of human mitral valves[J].Journal of Xiamen University(Natural Science),2016,55(2):272-277.(in Chinese)