向弱电网供电的VSC-HVDC系统的模拟惯量控制策略研究

张武其，吕 洋



向弱电网供电的VSC-HVDC系统的模拟惯量控制策略研究

张武其，吕 洋

(中国南方电网超高压输电公司柳州局, 广西 柳州 545006)

针对采用VSC-HVDC向弱电网供电时，受端弱电网惯量不足而出现扰动下暂态频率偏移较大的问题，提出了一种模拟惯量控制策略，以增大受端弱电网的惯量，从而提高系统的频率质量。为此，在对比换流站直流侧电容和同步发电机转子储能特性的基础上，建立了直流电压与系统频率的映射关系，从而得出了换流站所模拟惯量的具体计算等式。利用PSCAD/EMTDC就三种扰动下对VSC-HVDC逆变侧换流站分别采用传统控制和所提模拟惯量控制时进行了仿真比较。仿真结果表明，所提模拟惯量控制策略能够减小扰动下受端弱电网暂态频率偏移，提高受端弱电网的频率质量。

VSC-HVDC；频率响应；模拟惯量；故障穿越；弱电网

0 引言

基于电压源型换流器 (Voltage source converter, VSC)的高压直流输电(High voltage direct current, HVDC)采用可关断型功率开关器件与脉冲宽度调制(Pulse width modulation, PWM)技术。VSC-HVDC系统可以实现有功功率和无功功率解耦控制；同时其换流站无需交流系统提供换相容量，使得它在向无源或弱电网系统供电领域有着广阔的应用前景[1-4]。然而，在受端系统为无源或弱电网系统时，其系统惯性较小[5]。因此，扰动下受端电网频率在动态响应过程中易产生较大的暂态频率偏移，从而易引起低频减载装置误动作[6]。

为减少风电在电力系统中渗透率的不断增大而带来对系统频率稳定性的不利影响，文献[7]提出了一种针对DFIG风电机组的虚拟惯性控制策略，仿真验证了不同工况下所提控制策略对电网频率的支撑作用。文献[8]基于模糊逻辑控制提出了一种利用储能装置补偿风电场惯量的控制方法，有效改善了风电场响应系统频率变化的速度。为提高风电场故障穿越能力，文献[9]根据VSC-HVDC直流侧电压波动率，提出了一种基于风电机组惯性支持的故障穿越方法。在微电网中，采用逆变器接口的微电网电源因不含机械转子而缺少惯量[10]。为此，文献[11]提出了采用虚拟同步发电机思想的微电网逆变电源控制策略，有效提高了微电网供电电能质量，但未讨论该控制方法对系统频率稳定性的影响。文献[12]提出了基于虚拟惯性频率控制的微电源控制策略，并就该控制策略可能引发的微电源间的功率振荡问题进行了分析。为实现虚拟同步发电机有功、无功的跟踪控制，文献[13]提出了完整的虚拟同步发电机有功、无功调节控制器，并给出了惯性和阻尼参数的整定方法。此外，为提高VSC-HVDC受端弱电网的惯性，文献[14]提出了一种功率同步控制策略，有效提高了系统故障穿越能力。

基于以上分析，为提高VSC-HVDC系统受端弱电网系统的惯量，本文提出了一种借助VSC- HVDC系统直流侧电容储能特性的模拟惯量控制策略。该方法有效提高了扰动下VSC-HVDC受端弱电网系统供电的频率质量，且只需相对较小的直流电容就能实现模拟较大范围变化的惯性时间常数，并给出了模拟惯量时间常数计算等式。此外，不同于文献[15]，所提模拟惯量控制不依赖于dd的测量。最后，借助PSCAD/EMTDC就受端弱电网系统不同扰动下进行仿真验证与分析。仿真结果表明，所提模拟惯量策略能有效减少受端弱电网系统扰动下的暂态频率偏移，提高VSC-HVDC供电系统的故障穿越能力。

1  VSC-HVDC系统建模与控制

1.1 VSC-HVDC系统描述

图1给出了向弱电网供电的VSC-HVDC系统单相结构示意图。图1中，阻抗+j表示公共耦合点(Point of common coupling，PCC)与换流站间的等值阻抗(包括换流变压器和相阻抗器)；交流滤波器和相阻抗器用于滤除换流站开关产生的高频分量；直流电容则用于维持直流电压恒定以及为换流站提供能量平衡。弱受端电网包括异步电机IM1和IM2，本地同步发电机SG和固定线性负载Load1以及可变负载Load2。

图1 VSC-HVDC系统单相结构图

1.2 内环电流控制

图2给出了一端VSC连接交流电网系统的等值模型。图中sabc,dc,cabc,sabc分别为VSC交流侧电流、VSC直流电压、VSC交流侧端口电压和交流电网电压。在abc三相静止坐标系中，VSC交流侧动态数学方程为[16]

由坐标变换，则式(1)又可写为

(2)

式中，p和i为PI控制参数。

图2 VSC三相等值模型

Fig. 2 Three-phase VSC equivalent model

1.3 外环控制

VSC-HVDC控制系统常采用级联控制方式，由外环控制器和内环电流控制器组成。其中，外环控制器主要是为内环电流控制提供合适的电流参考值，包括有功功率控制、无功功率控制、直流电压控制以及交流电压控制[17]。此外，为确保系统稳定运行，必须保证内环控制器的速度大于外环控制器的速度。

综上所述，图3给出了VSC-HVDC传统控制系统框图。

图3 VSC-HVDC传统控制系统框图

2  模拟惯量控制

2.1 机械惯性时间常数与电容时间常数

同步发电机角速度随输入功率变化的响应速度，取决于其惯性时间常数，可写为[18-19]

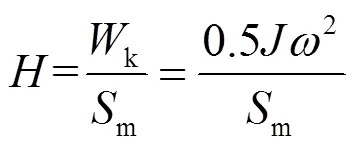
式中：为同步发电机转动惯量；k为同步发电机转子的动能；m为同步发电机额定容量。

VSC-HVDC系统中直流侧电容用于维持直流电压恒定以及为换流站提供能量平衡，其大小取决于时间常数[20]。

式中：VSC为换流站额定容量；E为电容器静电能量；为单个电容器电容值；为直流侧电容器个数。

对比式(4)和式(5)可知，VSC-HVDC直流电压dc类似于同步发电机SG角速度。因此，可将VSC-HVDC系统直流侧电容电压等效为发电机转子角速度。

2.2 模拟惯量控制

根据牛顿第二定律，发电机转子运行方程为[18]

式中：0为系统额定频率；M和E分别为机械功率和电磁功率标幺值。

由式(4)和式(5)可知，VSC-HVDC系统中直流侧电容储能特性和发电机转子储能特性相似。因而，可利用直流侧电压映射出电网系统频率，从而使换流站具有同步发电机特性。VSC-HVDC直流侧电容器动态方程为

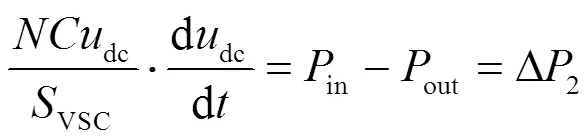
式中：in为直流侧电容输入功率标幺值；out为换流器输出功率标幺值。

为使VSC-HVDC系统换流站模拟同步发电机惯量，令直流电容功率变化量D1等于同步发电机功率变化量D2，结合式(6)和式(7)可得

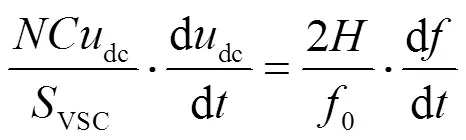
同时对式(8)两边积分，可得

(9)

式中：dc0为VSC-HVDC系统额定直流电压；VSC为换流站模拟的惯量时间常数。通过进一步处理，式(9)又可写为式(10)。

由式(10)可知，若VSC-HVDC系统换流站所模拟的惯量越大，则其直流电压的变化率也相对会较大，而扰动下系统频率可靠性越高。因此，要在满足系统设计要求的基础上，选取合适大小的模拟惯量。

因此，基于VSC-HVDC模拟惯量控制的数学模型为

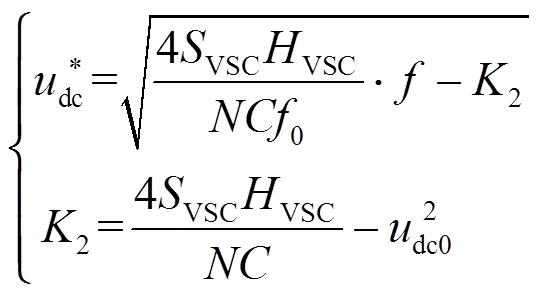
此外，所提模拟惯量控制策略同样适合于VSC-MTDC系统。但是针对两端VSC-HVDC系统，不宜在两端换流站同时都采用模拟惯量控制策略，其会恶化直流电压的稳定性和直流线路功率控制。

综上所述，包含模拟惯量控制的VSC-HVDC控制系统如图4所示。

图4 基于模拟惯量控制的VSC-HVDC控制系统框图

3  仿真分析

本文借助PSCAD/EMTDC建立了如图1所示的基于VSC-HVDC向弱电网供电的仿真系统。其中，VSC-HVDC系统参数与受端电网参数分别如表1和表2所示；固定线性负载为12.526 MW；可变负载为6 MW。整流站采用定有功功率控制和定无功功率控制；而逆变站采用本文所提的控制策略如图4所示。为了验证所提模拟惯量控制的有效，及其对受端弱交流系统频率的支持能力，仿真比较了受端电网相同扰动下，不同大小模拟惯量时间常数VSC对受端电网的影响。

表1 VSC-HVDC系统参数

表2 受端电网系统参数

3.1 负荷突变仿真分析

图5给出了4 s时刻负荷增加6 MW时直流电压、受端换流站输出功率、本地发电机输出功率及系统频率的仿真波形。由图5可知，负荷增加时，基于传统控制策略下，系统频率迅速跌至49.3 Hz，之后又恢复到49.47 Hz；而采用模拟惯量控制时，等效增加了受端电网转动惯量，系统频率从50 Hz缓慢降至49.47 Hz，从而可有效减小电网的暂态频率偏移。此外，由直流电压波形图可知，换流站所模拟的惯量越大，则在负荷增加瞬间其直流电压变化量越大，且换流站瞬间输出功率也越大。因此，模拟惯量时间常数并非越大越好。

图5 基于模拟惯量控制下负荷增加6 MW时仿真波形图

图6给出了4 s时刻负荷减少6 MW时直流电压、受端换流站输出功率、本地发电机输出功率及系统频率的仿真波形。由图6可知，负荷减少时，基于传统控制策略下，系统频率迅速升至50.62 Hz，然后慢慢回落至50.49 Hz左右；而在模拟惯量控制作用下，系统频率从50 Hz缓慢且无超调增至50.49 Hz左右。由此可知，本文所提模拟惯量控制能有效提高VSC-HVDC向弱电网系统供电的频率质量。同理，若受端换流站模拟惯量越大，则负荷减少瞬间直流电压变化越大。

图6 基于模拟惯量控制下负荷减少6 MW时仿真波形图

3.2 受端电网三相短路故障仿真分析

图7给出了4 s时刻受端电网PCC2母线处发生三相接地故障且持续时间为0.05 s时系统直流电压、受端换流站输出功率、本地发电机输出功率、及系统频率的仿真波形。从图7可知，基于传统控制策略下，由于采用定直流电压控制，导致故障瞬间系统频率大幅波动，而直流电压波动较小；而基于模拟惯量控制作用下，故障瞬间系统频率基本能维持在50 Hz左右。同时，由于系统阻尼较足，本地同步发电机受短路故障影响相对较小，而系统直流电压波动较大。总之，模拟惯量控制能有效提高VSC-HVDC向弱电网络的供电的频率质量和受端弱电网系统的抗扰动能力。

图7 基于模拟惯量控制下三相短路故障时仿真波形图

4  结论

本文研究了向弱电网系统供电的VSC-HVDC模拟惯量控制策略，得到如下结论：

(1) 弱交流电网本身惯量小，因此扰动下受端电网暂态频率偏移较大，易引起低频减载保护误动作；

(2) 由VSC-HVDC系统直流侧电容储能特性和发电机转子储能特性，建立了直流电压与系统频率的映射关系，从而得出了换流站所模拟惯量关于直流电压和系统频率的数学函数；

(3) 所模拟惯量并非越大越好，模拟惯量越大，扰动下直流电压波动越大；

(4) 所提模拟惯量时间常数可依据系统所允许的直流电压波动范围，求出其具体的取值范围；

(5) 相比于传统控制系统，模拟惯量控制明显减小了扰动下受端弱电网暂态频率偏移，提高了受端电网频率质量。

[1] 孙晓云, 同向前, 高鑫. 柔性直流输电系统中IGBT阀的故障诊断方法[J]. 电工技术学报, 2014, 29(8): 235-241.

SUN Xiaoyun, TONG Xiangqian, GAO Xin. Research on the fault diagnosis of IGBT valve in VSC-HVDC[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 235-241.

[2] 易荣, 岳伟, 张海涛, 等. 多端柔性直流输电系统中混合运行方式分析[J]. 电网与清洁能源, 2014, 30(12): 21-26.

YI Rong, YUE Wei, ZHANG Haitao, et al. Analysis on mixture operation mode of VSC-MTDC transmission system[J]. Power System and Clean Energy, 2014, 30(12): 21-26.

[3] 蒋冠前, 李志勇, 杨雪霞, 等. 柔性直流输电系统拓扑结构研究综述[J]. 电力系统保护与控制, 2015, 43(15): 145-153.

JIANG Guanqian, LI Zhiyong, YANG Xuexia, et al. Research review on topological of flexible HVDC system [J]. Power System Protection and Control, 2015, 43(15): 145-153.

[4] 王振浩, 李洋, 高凯, 等. 引入故障恢复信号的VSC- HVDC附加阻尼控制研究[J]. 电力系统保护与控制, 2015, 43(21): 34-40.

WANG Zhenhao, LI Yang, GAO Kai, et al. Study of using fault recovery signal for additional damping controller of VSC-based HVDC transmission system[J]. Power System Protection and Control, 2015, 43(21): 34-40.

[5] ZHANG L, HARNEFORS L, NEE H. Interconnection of two very weak AC systems by VSC-HVDC links using power-synchronization control[J]. IEEE Transactions on Power Systems, 2011, 26(1): 344-355.

[6] 徐泰山, 薛禹胜. 暂态频率偏移可接受性的定量分析[J]. 电力系统自动化, 2002, 26(19): 7-10.

XU Taishan, XUE Yusheng. Quantitative assessments of transient frequency deviation acceptability[J]. Automation of Electric Power Systems, 2002, 26(19): 7-10.

[7] 李和明, 张祥宇, 王毅, 等. 基于功率跟踪优化的双馈风力发电机组虚拟惯性控制技术[J]. 中国电机工程学报, 2012, 32(7): 32-39.

LI Heming, ZHANG Xiangyu, WANG Yi, et al. Virtual inertia control of DFIG-based wind turbines based on the optimal power tracking[J]. Proceedings of the CSEE, 2012, 32(7): 32-39.

[8] 刘巨, 姚伟, 文劲宇, 等. 一种基于储能技术的风电场虚拟惯量补偿策略[J]. 中国电机工程学报, 2015, 35(7): 1596-1605.

LIU Ju, YAO Wei, WEN Jinyu, et al. A wind farm virtual inertia compensation strategy based on energy storage system[J]. Proceedings of the CSEE, 2015, 35(7): 1596-1605.

[9] 王毅, 付媛, 苏小晴, 等. 基于VSC-HVDC联网的风电场故障穿越控制策略研究[J]. 电工技术学报, 2013, 28(12): 150-159.

WANG Yi, FU Yuan, SU Xiaoqing, et al. Fault ride- through control strategy of wind farm integrated with VSC-HVDC[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 150-159.

[10] VISSCHER K, DE HAAN S W H. Virtual synchronous machines (VSGs) for frequency stabilization in future grids with a significant share of decentralized generation[C] // Proceedings of CIRED Seminar: Smart Grids for Distribution, 2008.

[11] 丁明, 杨向真, 苏建徽. 基于虚拟同步发电机思想的微电网逆变电源控制策略[J]. 电力系统自动化, 2009, 33(8): 89-93.

DING Ming, YANG Xiangzhen, SU Jianhui. Control strategies of inverters based on virtual synchronous generator in a microgrid[J]. Automation of Electric Power Systems, 2009, 33(8): 89-93.

[12] 杜威, 姜齐荣, 陈蛟瑞. 微电网电源的虚拟惯性频率控制策略[J]. 电力系统自动化, 2011, 35(23): 26-31.

DU Wei, JIANG Qirong, CHEN Jiaorui. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems, 2011, 35(23): 26-31.

[13] 吕志鹏, 盛万兴, 钟庆昌, 等. 虚拟同步发电机及其在微电网中的应用[J]. 中国电机工程学报, 2014, 34(16): 2591-2603.

LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.

[14] ZHANG Lidong, HARNEFORS L, NEE H P. Modeling and control of VSC-HVDC links connected to island systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 783-793.

[15] MIAO Zhixin, FAN Lingling, OSHBORN D, et al. Wind farms with HVDC delivery in inertial response and primary frequency control[J]. IEEE Transactions on Energy Conversions, 2010, 25(4): 1171-1178.

[16] 边晓燕, 王本利, 陈建平, 等. 改进的DFIG与VSC-HVDC协调控制改善风电场低电压穿越能力[J]. 电力系统保护与控制, 2016, 44(1): 9-16.

BIAN Xiaoyan, WANG Benli, CHEN Jianping, et al. Improvement of low voltage ride through capability of wind farm using coordinated control of the improved DFIG and VSC-HVDC[J]. Power System Protection and Control, 2016, 44(1): 9-16.

[17] DU Cuiqing, SANNIO A, BOLLEN H J M. Analysis of the control algorithms of voltage-source converter HVDC[C] // IEEE Power Tech, Petersburg, Russia, 2005.

[18] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.

[19] 鲍正杰, 李生虎. 基于VSC-HVDC 有功支援和自适应低频减载的区域电网频率控制[J]. 电力系统保护与控制, 2014, 42(20): 32-37.

BAO Zhengjie, LI Shenghu. Frequency control for regional system based on active power support from VSC-HVDC and adaptive under-frequency load shedding[J]. Power System Protection and Control, 2014, 42(20): 32-37.

[20] JIANG Y. Active and reactive power control of transmission systems with voltage source converter[D]. Stockholm, Sweden: Roy Inst Technol, 1997.

(编辑 姜新丽)

Emulation inertia control strategy for VSC-HVDC supplying weak network

ZHANG Wuqi, LÜ Yang

(Liuzhou Bureau, China Southern Power Grid EHV Power Transmission Company, Liuzhou 545006, China)

When the VSC-HVDC transmission system is employed to the weak grid, which is comparatively lower or no inertia, hence the large transient frequency deviation problem is always happened under the disturbances. In order to increase the inertia of the receiving grid, this paper proposes a emulation inertia control strategy, which significantly improves the system frequency quality. Based on the comparisons between the DC capacitance of the converter and the energy storage features of synchronous generator rotor, the relationship between DC voltage and system frequency is built. And then the specified formula for the emulation inertia calculation is given. The inverter station of the VSC-HVDC system with conventional control strategy and the proposed emulation inertia control strategy respectively is tested under different disturbances using PSCAD/EMTDC. Simulation results show that the proposed emulation inertia control strategy can better suppress the fluctuation frequency under the disturbances and improve the system frequency quality.

VSC-HVDC; frequency response; emulation inertia; fault ride-through; weak grid

10.7667/PSPC150845

2015-07-19；

2016-01-15

张武其(1990-)，男，硕士，研究方向为电力电子在电力系统中的应用；E-mail:wuqi_zhang@126.com 吕 洋(1989-)，男，硕士，研究方向为高电压与绝缘技术。E-mail: 54lvyang@163.com