列车荷载作用下无砟轨道层间裂缝内水压力分布
2016-04-10曹世豪杨荣山刘学毅
曹世豪,杨荣山,刘学毅,谢 露,栗 行
(西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031)
无砟轨道以其高平顺、高稳定和少维修的特点成为高速铁路的主要轨道结构形式,得到了快速发展与广泛应用。但无砟轨道服役过程中,在列车和温度荷载的作用下,轨道结构会产生裂缝[1-2]。在这些裂缝中,轨道结构层间裂缝对轨道的整体性影响最大;在降水量较少地区,裂缝发展相对缓慢,但在降雨量丰富的地区或排水不畅地段,裂缝扩展速率较快[2-5]。可见,裂缝内水压力的作用对无砟轨道内裂缝扩展起着极为关键的作用。
关于混凝土内水压力的研究,大部分集中于混凝土重力坝领域。徐世烺和Slowik等[6-9]通过机械荷载与静水压力耦合作用下的水力劈裂试验,研究了不同静水压作用下裂缝扩展中的水压力分布,并得出裂缝内的静水压力会降低结构的承载能力。李宗利和Tinawi等[10-11]在假设裂缝面为刚性面的前提下对混凝土结构裂缝内水压力分布进行了理论研究。黄云等[12]研究了水压力分布形式对混凝土初始裂缝扩展的影响。
以上研究多以静水压力作用为主,而仅有的少量动水压力研究也比较粗糙,难以反映无砟轨道承受荷载大、频率高的特点,致使上述研究成果不能照搬到无砟轨道的相关研究领域。此外,由于水压力的产生和作用机理的复杂性,目前国内外在无砟轨道领域对相关问题仅有初步的研究[3-5]。因此,开展列车荷载作用下无砟轨道层间裂缝内水压力分布的理论与试验研究,并考虑裂缝内空气存在对压力分布的影响,明确荷载幅值、荷载频率等与水压力之间的关系,为进一步分析无砟轨道层间裂缝在列车荷载与水耦合作用下的扩展提供依据。
1 裂缝内动水压力产生机理分析
无砟轨道轨道板与支撑层间裂缝及其内水、空气的流动和压力分布情况如图1所示。图中:v为轨道板下压速度,L为裂缝深度,Lap为加载后裂缝中空气的深度,Lsta为驻点到裂缝起点的距离,pai为裂缝出口处的绝对压强,pap为空气与水交界面处的压强(与整个空气域的压强pair相等),psta为驻点处水的压强。
无砟轨道层间含水裂缝随着列车的趋近与离开会发生周期性的张开与闭合。列车的趋近和远离分别对应了裂缝的加载和卸载过程。在裂缝内充满水的情况下,加载会使裂缝内的空间减小,此时裂缝内的水因受到裂缝面的挤压而被排出;由质量守恒定律可知,沿着裂缝出口方向水流速度会逐渐增加,即流体的动量呈增加趋势;由动量定理可知,控制体的合力方向与动量增加的方向一致;由此可见,水压力由里往外逐渐减小,即水压力最大值发生在裂缝尖端处,如图1(a)所示。同理,卸载时,由于裂缝空间的增加使得流体由裂缝出口处流入裂缝内,此时水压力沿着裂缝出口方向呈增加趋势,水压力最小值发生在裂缝尖端处,如图1(b)所示。
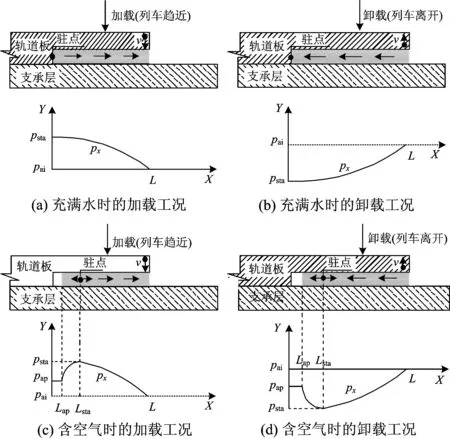
图1 裂缝及其内水、空气的流动和压力分布
实际上,裂缝尖端处可能会存在少量的空气,即裂缝内未能全部充满水,称为不饱和含水裂缝。在列车荷载作用下,饱和含水裂缝内的动压力分布是较为典型的液、固二相耦合振动问题,而不饱和含水裂缝内的动压力分布是较为典型的液、固、气三相耦合振动问题。在不饱和含水裂缝内距离裂缝尖端一定距离处,会存在1个流速为0的点,本文称之为驻点,如图1(c)和(d)所示。加载时,流体由驻点向2个相反的方向流动,此时水压力最大值发生在驻点位置,并沿着2个相反的方向呈减小趋势,如图1(c)所示。卸载时,流体由两边向驻点处汇流,此时水压力最小值发生在驻点的位置,并沿着2个相反的方向呈增加趋势,如图1(d)所示。驻点的位置并不是固定不变的,而是会随着裂缝内空气的初始体积变化而改变[13]。
2 裂缝内动水压力分布公式推导
2.1 基本假设
理论上,采用N-S方程和连续性方程,结合一定的初始条件和边界条件,就可以对流场进行准确的描述,然而由于边界条件的复杂性和数值计算上的困难,目前只能对一些简单问题求解,而对于大多数问题,往往需要简化模型[10]。
针对无砟轨道不饱和含水裂缝内动水压力分布问题,为了简化模型,提出如下基本假设:①水为不可压缩,无黏性的理想流体;②裂缝内空气为理想气体;③忽略裂缝壁渗透损失量;④裂缝开口量远小于其他2个方向的长度;⑤忽略流体沿轨道纵向的流动。基于以上假设,可将复杂的三维流动问题简化为平面问题。
2.2 裂缝内水的速度分布微分方程
图2给出了放大的裂缝变形示意图,图中h为裂纹初始开口量,wx为加载后x处的裂缝开口量(因本文研究均指任意时刻流体状态,为了简单,省略下标t,以下类同),ux为加载后x处的裂缝上表面位移,Lai为初始时不饱和含水裂缝内的空气深度,F(t)为作用荷载。

图2 裂缝变形示意图(放大)
由于在列车荷载作用下轨道板的变形很小,在弹性范围内,因此裂缝上表面的位移ux可表示为
ux=β(x)F
(1)
式中:β(x)为变形系数,与裂缝深度和荷载作用的位置有关。
由图2可知,初始时单位长度裂缝内空气域的初始体积Vai为
Vai=Laih
(2)
此时,由于裂缝内空气、水与裂缝出口处水的绝对压强pai处于平衡状态,因此裂缝内水和空气的初始压强与裂缝出口处水的绝对压强pai相等。
经历时间t后,空气与水的交界面由Lai移动到Lap,由水的不可压缩性可知,体积1与体积2相等,则

(3)
其中,wx=h+ux=h+Fβ(x)
此时空气域的体积变化量ΔV为
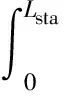
(4)
由理想气体状态方程可知,在气体物质的量与温度保持不变时,气体的压强p与体积V的乘积为常数[5],即
pV=C
(5)
由式(2)、式(4)和式(5)可得列车荷载作用下t时刻空气域的压强pair为
(6)
此时,由空气与水交界面处的压强pap与空气域压强相等可得
pap=pair
(7)

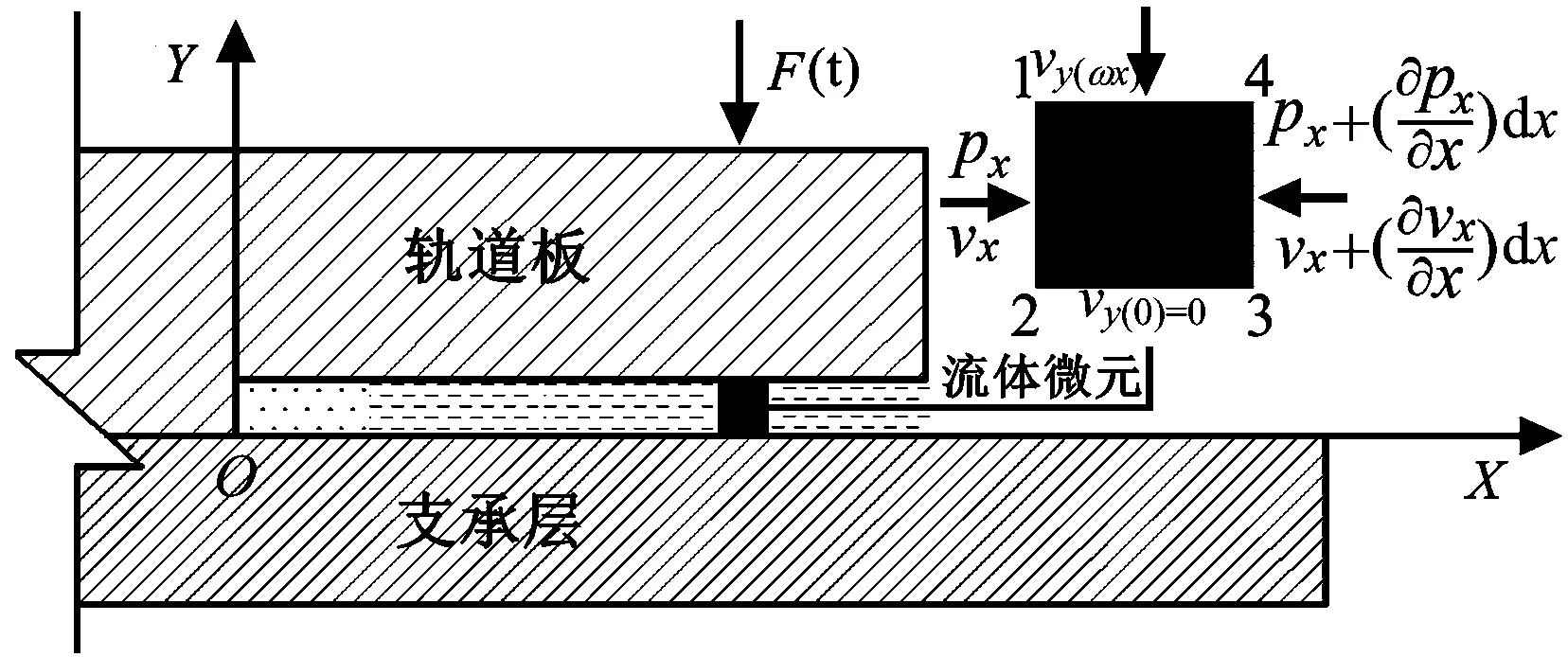
图3 无砟轨道不饱和含水裂缝及流体微元
在微小时间dt内,净流入控制体的总质量m为
(8)
由质量守恒原理可知,净流入控制体的总质量等于控制体内流体质量的增量,即
(9)
裂缝上表面的速度vy可由裂缝上表面的位移对时间求导得到
(10)
对于不可压缩流体,其密度ρ为常数,将式(10)带入式(9)中化简得
(11)
式(11)即为根据质量守恒定律求得的列车荷载作用下无砟轨道层间裂缝内水的速度分布微分方程。
2.3 裂缝内水的压力分布微分方程
由图3可知,流体微元x方向上的合力为
(12)
根据牛顿第二定律(F=ma),沿x方向有
(13)
化简得
(14)
式(14)即为根据牛顿第二定律求得的列车荷载作用下无砟轨道层间裂缝内水的压力分布微分方程。
2.4 边界条件
在驻点(x=Lsta)处
vx(Lsta)=0
(15)
在裂缝内空气与水的交界处,其压强等于空气域的压强pair,则
px(Lap)=pap=pair
(16)
在裂缝出口处,其压强等于液体的绝对压强,即
px(L)=pai
(17)
2.5 裂缝内各区域压力分布解析式
在x=0~Lap区域内,空气域压强为
(18)
在x=Lap~Lsta区域内,由裂缝内水流速度微分方程(11)、水压力分布微分方程(14)及边界条件式(15)和式(16)可求得裂缝内此区域水的压力分布式
(19)
同理,在x=Lsta~L区域内,由式(11)、式(14)、式(15)和式(17)可求得裂缝内此区域水的压力分布式
(20)
当裂缝内空气的初始体积确定时,通过式(18)、式(19)和式(20)即可求出整个裂缝内不同区域水的压力分布,如图1(c)和(d)所示。
在式(21)所示列车荷载作用下,郴饱和含水裂缝内x=Lsta~L区域水的压力计算式(20)可化为式(22)所示形式。
F=Fm+Fof(ωt)
(21)
式中:Fm为荷载平均值;Fo为荷载幅值;ω为荷载频率;f(ωt)为周期函数。
(22)
由式(22)可知,对于无砟轨道层间不饱和含水裂缝,在列车荷载作用下,当驻点位置Lsta确定不变时,裂缝内水压力与荷载频率呈二次方关系,与荷载幅值呈线性关系。当裂缝内充满水时,驻点位置在裂缝尖端处,此时的动水压力变化规律与不饱和含水裂缝内Lsta~L区域的是一致。
3 试 验
3.1 试验装置
列车荷载作用下无砟轨道层间裂缝内动水压力分布试验系统主要由水槽、含裂缝混凝土试件、荷载加载系统、水压力传感器及数据采集系统组成,如图4所示。

图4 试验装置
水槽内覆盖一层防水塑料布,避免试验时水的渗出;防水塑料布上铺设一层橡胶垫,避免试件对防水塑料布的破坏。水槽中注入20 ℃的自来水,水位要淹没裂缝。
共制作含裂缝混凝土试件9个,混凝土标号为C40,试件尺寸如图5所示。裂缝位于轨道板与支承层界面处,长500 mm,深300 mm,开口量3 mm。

图5 试件尺寸及测点布置图(单位: mm)
试验荷载由250 kN万能伺服液压疲劳试验机施加,荷载形式为正弦波,其中均值为45 kN,振幅为20 kN;荷载频率ω取1~10 Hz,以1 Hz为梯度逐级加载。
混凝土试件裂缝内的水压力采用高精度数字压力传感器测量,传感器的测量精度为1 Pa,采样间隔为10 ms。压力传感器的一侧接塑料导管(导管的长度根据实际测点位置深度截取),导管口置于裂缝内水压力测点位置,测点布置如图5(c)所示;压力传感器的另一侧通过数据线、采集卡、USB接口等连接电脑,电脑上安装的数据采集软件可直接绘制出水压力—时间关系曲线。
3.2 试验结果及分析
3.2.1水压力随时间的变化
图6给出了在频率为6 Hz的荷载作用下,测点5的水压力时程曲线。

图6 测点5的水压力时程曲线
由图6可知:在频率为6 Hz的荷载作用下,裂缝内水压力在1 s内出现了6次周期性变化,即水压力的变化周期与荷载的变化周期保持一致;而在同一变化周期内,水压力分别出现了1次最大正压力和1次最大负压力,分别对应试验中加载和卸载峰值时刻;其中最大正压力值为531 Pa,最小负压力值为-538 Pa;正负水压力峰值的绝对值之间的微小差别主要是由水压力传感器的测量精度偏差引起的。
3.2.2水压力沿裂缝的分布
图7给出了在不同频率列车荷载作用下,裂缝内水压力峰值试验结果。

图7 水压力试验结果
由图7可知:沿着裂缝出口方向,水压力先增加后减小,最大水压力并不是发生在裂缝尖端位置,而是发生在距裂缝尖端一定距离的位置,即理论分析中驻点的位置,如在6 Hz的动荷载作用下水压力的最大值发生在距离裂缝尖端0.09 m的位置,即其驻点位置Lsta=0.09 m。这与理论分析中不饱和含水裂缝在列车荷载作用下的裂缝内水压力分布规律是一致的,也就是说水压力在裂缝尖端附近区域减小的原因是因为少量空气的存在导致。由图7还可看出,随着荷载频率的增加,水压力呈增加趋势,且水压力增加的趋势随荷载频率的增加而越加明显。其原因是随着荷载频率的增加,裂缝上表面对水的挤压越加迅速,导致流体的流速也迅速增加;导致流体速度增加的驱动力主要是由压力梯度提供;因此,随着荷载频率的增加,水压力呈增加趋势。
理论分析表明,当驻点位置确定不变时,裂缝内水压力与加载频率呈二次方关系;而由图7(a)中3和6 Hz的水压力分布可以看出,其最大值位置基本都发生在距离裂缝尖端0.09 m的位置,即2种频率荷载作用下驻点位置是一致的。
表1给出了在3和6 Hz列车荷载作用下裂缝内距尖端不同距离处的水压力。由表1可知:在频率为6 Hz的荷载作用下,不同测点的水压力大致是频率为3 Hz荷载作用下的4倍,这与理论分析得到的水压力与加载频率呈二次方关系的结果基本一致。
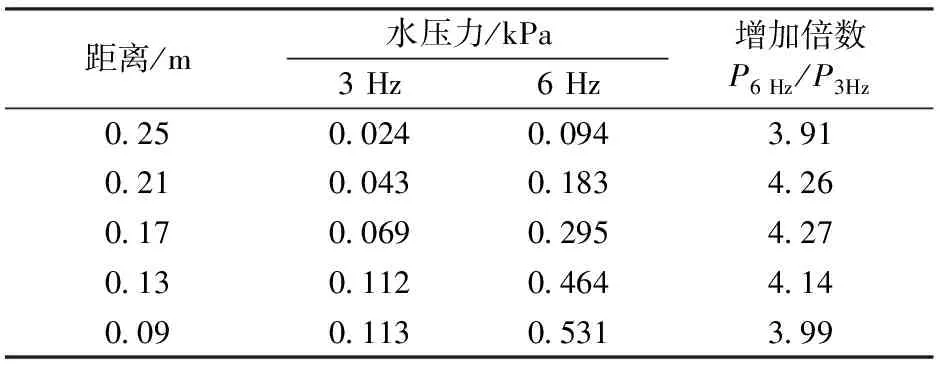
表1 不同频率荷载作用下的水压力
综合上述分析可知,在列车荷载作用下,荷载频率是影响无砟轨道层间裂缝内水压力的重要因素;随着荷载频率的增加,水压力呈增加趋势,且基本与加载频率呈二次方关系。
4 结 论
(1) 考虑裂缝内空气的影响时,裂缝内水压力分布可由空气与水的交界面、驻点位置分为3个阶段;加载时,水压力最大值发生在驻点位置,并沿着2个相反的方向呈减小趋势;卸载时,水压力最小值发生在驻点的位置,并沿着2个相反的方向呈增加趋势。
(2) 在列车荷载作用下,荷载频率是影响无砟轨道层间裂缝内水压力的重要因素;随着荷载频率的增加,水压力呈增加趋势,且水压力大小与加载频率基本呈二次方关系。
(3) 动水压力的变化规律与荷载周期保持一致,在同一荷载周期内,随着荷载的加载和卸载,裂缝内水压力分别出现1次最大正压力和1次最小负压力。
[1]刘钰,赵国堂. CRTSⅡ型板式无砟轨道结构层间早期离缝研究[J]. 中国铁道科学,2013, 34(4): 1-6.
(LIU Yu, ZHAO Guotang. Analysis of Early Gap between Layers of CRTSⅡ Slab Ballastless Track Structure[J]. China Railway Science, 2013, 34(4): 1-6.in Chinese)
[2]杨荣山,段玉振,刘学毅. 双块式无砟轨道轨枕松动对轮轨系统动力性能影响研究[J]. 中国铁道科学,2014, 35(5): 13-18.
(YANG Rongshan, DUAN Yuzhen, LIU Xueyi. Influence Induced by Sleeper Looseness of Bi-Block Slab Track on Dynamic Property of Wheel-Track System[J]. China Railway Science, 2014, 35(5): 13-18.in Chinese)
[3]徐静,洪锦祥,刘加平,等. CA砂浆泌水的影响因素分析[J]. 东南大学学报:自然科学版,2010, 40(2): 56-60.
(XU Jing,HONG Jinxiang, LIU Jiaping, et al. Research on Factors Influencing Bleeding of CA Mortar[J]. Journal of Southeast University:Natural Science Edition, 2010, 40(2): 56-60. in Chinese)
[4]颜华,胡华锋,曾晓辉,等. 静水作用下板式无砟轨道CA砂浆力学性能变化[J]. 高速铁路技术,2014, 5(4): 56-61.
(YAN Hua, HU Huafeng, ZENG Xiaohui, et al. Studies on Mechanical Changes of CA Mortar for Slab Track under Hydrostatic Effect[J]. High Speed Railway Technology, 2014, 5(4): 56-61.in Chinese)
[5]张凌之,徐坤,杨荣山. 双块式无砟轨道轨枕脱空处水的特性研究[J]. 铁道标准设计, 2014, 58(2): 17-21.
(ZHANG Lingzhi, XU Kun, YANG Rongshan. Research on Characteristics of Water Beneath Voided Sleeper in Bi-Block Ballastless Track System[J]. Railway Standard Design, 2014, 58(2): 17-21.in Chinese)
[6]徐世烺,王建敏. 静水压力下混凝土双K断裂参数试验测定[J]. 水利学报, 2007, 38(7): 792-798.
(XU Shilang, WANG Jianmin. Experimental Determination of Double-K Fracture Parameters of Concrete under Water Pressure[J]. Shuili Xuebao, 2007, 38(7): 792-798.in Chinese)
[7]SLOWIK V, SAOUMA V E. Water Pressure in Propagation Concrete Cracks[J]. Journal of Structural Engineering, 2000, 126(2): 235-242.
[8]SHINMURA A, SAOUMA V E. Fluid Fracture Interaction in Pressurized Reinforced Concrete Vessels[J]. Materials and Structures, 1997, 30(2): 72-80.
[9]BRHWILER E, SAOUMA V E. Water Fracture Interaction in Concrete-Part Ⅰ:Fracture Properties[J]. ACI Materials Journal, 1995, 92(3): 296-303.
[10]李宗利,任青文,王亚红. 岩石与混凝土水力劈裂缝内水压力分布的计算[J]. 水利学报, 2005, 36(6): 656-661.
(LI Zongli, REN Qingwen, WANG Yahong. Formula for Water Pressure Distribution in Rock or Concrete Fractures Formed by Hydraulic Fracturing[J]. Shuili Xuebao, 2005, 36(6): 656-661.in Chinese)
[11]TINAWI R, GUIZANI L. Formulation of Hydrodynamic Pressure in Cracks Due to Earthquakes in Concrete Dams[J]. Earthquake Engineering and Structural Dynamics, 1994, 23(7): 699-715.
[12]黄云,金峰,王光纶,等. 高拱坝上游坝踵裂缝稳定性及其扩展[J]. 清华大学学报:自然科学报, 2002, 42(4): 555-559.
(HUANG Yun, JIN Feng, WANG Guanglun, et al. Stability and Propagation of Cracks at the Heel of High Arch Dams[J]. Journal of Tsinghua University:Science and Technology, 2002, 42(4): 555-559.
[13]JAVANMARDI F, LÉGER P, TINAWI R. Seismic Structural Stability of Concrete Gravity Dams Considering Transient Uplift Pressures in Cracks[J]. Engineering Structures, 2005, 27(4): 616-628.
