斜拉桥拉索损伤模拟方法及其对索力和挠度分布规律的影响
2016-04-10葛俊颖苏木标
葛俊颖,苏木标
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.石家庄铁道大学 大型结构健康诊断与控制研究所,河北 石家庄 050043)
拉索是斜拉桥的关键受力构件,也是斜拉桥结构体系中最容易出现病害损伤的构件。在已发现的斜拉桥病害损伤中,出现在拉索上的病害占了绝大部分。斜拉桥的设计生命周期通常为100年,而拉索由于病害损伤多发,一般用15~20年就要全部更换一次。拉索的损伤对于斜拉桥结构的安全性、整体性以及静动力特性都会产生不利的影响。及早识别拉索损伤并及时采取必要的措施可有效地避免它对斜拉桥的不利影响,并保证桥梁结构安全运营。如何准确模拟拉索损伤对准确把握拉索损伤后斜拉桥的实际受力状况、动静力特性变化规律以及索力和主梁挠度的分布规律具有重要意义[1-4]。
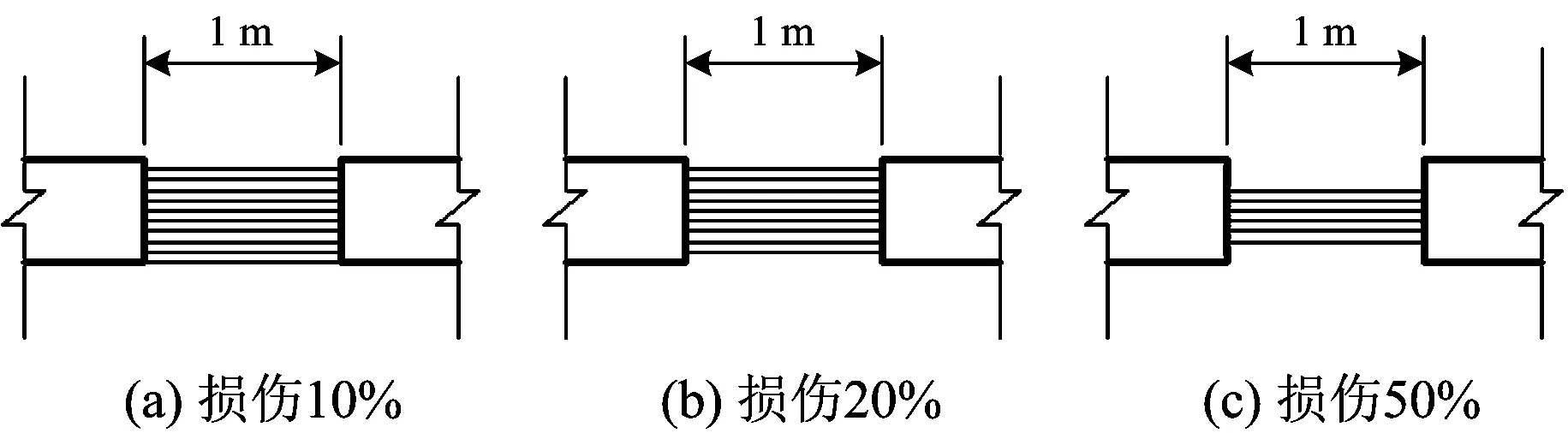
斜拉桥的拉索多采用平行钢丝束或钢绞线制作[2]。根据拉索的常见病害(见图1),本文将拉索的损伤按损伤程度的不同分为断丝损伤和未断丝的局部损伤2种情况分别进行模拟。对平行钢丝束拉索,断丝损伤是指某一根或多根钢丝完全断裂失效;对钢绞线拉索,断丝是指某一根或多根钢绞线整根断裂失效。断丝损伤的特点是拉索损伤后,断裂失效的钢丝或钢绞线与完好的钢丝或钢绞线之间没有约束,断裂的钢丝或钢绞线整根不再受力。局部损伤多为局部锈蚀,是指拉索中部分或全部钢丝或钢绞线都出现了损伤,但没有出现断丝,只是它们的截面被削弱。为了研究不同程度的锈蚀对拉索受力及主梁挠度的影响规律,根据锈蚀发展的方向将局部损伤分为2种:一是拉索锈蚀损伤被限定在一定长度范围内,仅在这一局部范围内考虑拉索的有效截面发生改变,即局部径向损伤;二是拉索发生锈蚀损伤后,认为拉索截面被削弱到某种程度并保持不变,考虑这一损伤分布的长度范围发生改变,即局部沿长损伤。

图1 斜拉桥拉索损伤
无论断丝损伤还是局部损伤都是在拉索具有很大的张力情况下发生的,拉索损伤的模拟必须体现其初始内力[5-6]。为了保证计算模型中拉索索力以及桥梁线形和实际状态一致,须建立斜拉桥基准模型[7]。拉索损伤可用面积折减法、弹模折减法、反向荷载法和实体单元法模拟,目前国内外常用的模拟方法是面积折减法和弹模折减法。
本文以邯武快速路上跨邯长铁路立交桥主桥为例,运用数值分析方法,研究斜拉桥拉索损伤模拟方法,以及拉索不同损伤状况和程度对拉索索力和主梁挠度分布规律的影响。
1 斜拉桥基准模型
在施工和运营过程中斜拉桥拉索索力及桥梁线形会偏离设计值,所以在进行数值分析时必要根据实测数据对计算模型进行修正,并以修正后的模型作为斜拉桥基准模型[8-9]。
1.1 索力修正
斜拉桥在无损伤状态时,其初始索力应为成桥状态恒载作用下的实际索力。为了与实测索力一致,可采用试算法[8-10]。首先将实测索力以初应变的形式加到斜拉索上,再加恒载计算。若计算所得的索力与实测索力的误差在允许误差范围内则停止计算,拉索初始索力即为最后一次计算时的初应变乘以考虑垂度效应修正后的弹性模量。若误差不在允许误差范围内,则将索力差值对应的应变增量加到原初应变上,重新计算直至误差在允许的范围内为止[9-11]。
为了解决试算法调索繁琐的问题,利用ANSYS二次开发技术开发斜拉桥调索程序,使调索过程在ANSYS中自动完成。在ANSYS模型中拉索面积用1个m(拉索总根数)行1列的数组A(i)表示,初应变用1个m行100列的数组S(i,j)表示(这里假设迭代次数小于100),索力用m行100列的数组F(i,j)表示,且
F(i,j)=EA(i)S(i,j)
i=1,2,…,m;j=1,2,…,100
(1)
式中:E为索的弹模。
修正前的j值取1,此时初应变为S(i,1), 对应索力为F(i,1)。 第1次修正后的j值取2, 第j-1次修正后的索力为F(i,j)。假设
B(i)=1-F(i,j)/F(i,1)
(2)
将第j-1次迭代后的索力与初始索力F(i,1)对比, 若误差B(i)不在容许范围内,则将初应变设置为
(3)
重新计算,依此循环迭代直至各索索力均满足容许误差要求。
1.2 主梁线形修正
除了修正斜拉索索力外,还需要对主梁线形进行修正[11-12]。具体方法根据找形分析原理:首先在索曲弦线位置建立计算模型,并在自重荷载和修正后的索力作用下对模型进行求解(设置较小的弹性模量和较大的初始应变以便快速收敛);然后比较所求得的主梁竖向线形与成桥实测线形的差值,并将该差值加到所求得的主梁竖向线形的相应位置,恢复实际的弹性模量。
1.3 基准模型建立步骤
第1步,根据实测索力采用上述试算法进行索力修正;
第2步,将实测主梁线形作为目标线形进行线形修正,线形修正后的索力会偏离上一次索力修正后的结果;
第3步,重复执行第1步和第2步,直至计算出的索力和线形分别与实测索力和实测线形的差值满足误差要求为止。
2 拉索断丝的数值模拟方法
2.1 面积折减法
一般来说,拉索断丝可视为其有效承载面积减小。所谓面积折减法,就是用面积的折减量表示拉索的锈蚀程度[13]。假设拉索在无锈蚀损伤状态下的受力面积为A,损伤后有效受力面积为A*,那么,拉索损伤程度用变量D表示为
(4)
D=0表示拉索无损伤;D=1表示拉索损伤殆尽(整根完全断裂);0 材料性能退化通常导致其弹性模量发生变化。拉索发生损伤主要导致其刚度系数(EA/l)发生变化,因此,也可以近似采用弹模折减法模拟拉索的损伤,也就是假设拉索损伤前后面积没有发生变化,而是通过折减弹性模量实现。根据Lemaitre界定的金属材料在单轴应力状态下疲劳损伤的应变等价原理[13-14]可知 (5) 式中:E为拉索无锈蚀状态下的弹性模量;E*为拉索锈蚀后的有效弹性模量。 若假设拉索的损伤为拉索刚度系数的改变,则采用弹模折减法模拟斜拉索损伤与面积折减法等价。ANSYS中模拟拉索损伤仍然采用在损伤索位置建立重复单元的方法,损伤索单元的有效弹性模量为E*=E(1-D),面积保持不变。 反向荷载法是指在损伤索的两端施加1对反向荷载,模拟拉索损伤后索力的减小。其原理为:假设拉索损伤前每根钢丝或钢绞线的应力σ相同,若单根钢丝或钢绞线的面积为Ai,则每断一根钢丝或钢绞线相当于瞬间拉索的索力减少量ΔF=Aiσ。若断丝n根,则在损伤索两端施加1对反向荷载ΔF=nAiσ。 利用ANSYS进行反向荷载法模拟时,可以在原基准模型上进行未损伤的初始分析,然后重新启动分析模拟拉索损伤。但须注意,在ANSYS中当施加不同于总体坐标系方向的荷载时,需要旋转相应的节点坐标系到需要的方向,然后再施加荷载。 用实体单元法模拟斜拉索的损伤时,为了尽可能缩小计算模型与原结构的偏差,只对损伤索及索塔另一侧与其对称位置的拉索采用实体单元模拟,其余非损伤索仍采用索单元模拟。也就是说,这种方法中模拟拉索同时采用了实体单元和索单元2种单元。用ANSYS建模时,将实体单元截面定义为正方形截面,单元划分时将正方形截面划分为若干小长方形(其数量由假设的损伤程度确定),索长方向的划分应保证最终划分结果为每个小单元均近似为长方体(长边长度与短边长度的比值最好小于2),通过杀死小长方体单元模拟索的损伤。不考虑拉索各钢丝间由于某些位置损伤可能产生的相互错动。索单元通过在实常数中设置初应变施加索力,而实体单元则通过降温法施加索力。降温法中的温降量等于环境温度与参考温度(需在拉索材料特性中设置)之差,环境温度默认为0。参考温度值按照式(6)进行设置。 (6) 式中:Δt为初始索力对应的温度增量,即默认情况下的参考温度;ε为模型初始索力对应的初应变;α为拉索材料的线膨胀系数。 拉索的初始拉力 (7) 式中:Δl为拉索的初始伸长量;l为索长。 对拉索局部损伤进行模拟分析的目的是为了分析拉索从钢丝或钢绞线刚开始锈蚀至发生断丝整个过程中其索力及主梁挠度的变化规律。在拉索内的钢丝发生锈蚀损伤但未断丝的情况下,采用实体单元法进行损伤模拟分析,先将拉索实体单元划分成相应的份数模拟不同的损伤率,通过杀死局部的实体单元实现拉索的局部损伤。 假设某拉索发生局部锈蚀损伤,其截面被削弱到某种程度(如50%),且保持不变,并考虑损伤分布在不同的长度范围内。损伤索沿索长方向不同程度的损伤示意如图2所示。 假设某拉索发生的局部锈蚀损伤仅限于一定长度范围(比如1 m)内,不向长度方向发展,但其截面被削弱程度不断发展,即拉索在局部范围内截面积发生不同程度的减小,如图3所示。 图2 拉索沿长度方向损伤示意图 图3 拉索沿径向损伤示意图 为了寻找拉索断丝和局部损伤对斜拉桥索力和主梁挠度分布规律的影响,以邯武快速路上跨邯长铁路立交桥主桥为例进行分析。该桥为独塔双索面斜拉桥,跨度2×130 m,采用塔梁固结形式。主梁为单箱四室预应力钢筋混凝土箱梁,索塔为H型塔,采用钢筋混凝土结构,索塔总高度为93.20 m。斜拉索采用扇形布置,采用平行钢丝索,梁上索距6 m,桥塔两侧各有18对斜拉索。 建模时,墩、塔和主梁均采用三维梁单元模拟,单元数量338;根据不同的损伤模拟方法,采用不同类型单元模拟拉索。用面积折减法、弹模折减法、反向荷载法模拟拉索损伤时采用索单元,用实体单元法模拟拉索损伤时则同时采用实体单元和索单元。计算模型如图4所示。 图4 斜拉桥计算模型 全桥共有36对拉索,桥塔左侧的拉索编号从右至左依次为C1—C18,桥塔右侧的拉索编号从左至右依次为S1—S18。主梁在斜拉索的锚点处设置有横梁,锚点对应的主梁节点编号在桥塔左侧从右至左依次为BC1—BC18,在桥塔右侧从左至右依次为BS1—BS18,C18左侧的无索梁段节点编号为B1和B2,S18右侧无索梁段节点编号为B82和B83,C1和S1之间的无索梁段节点编号为B40—B44。计算工况见表1。 表1 计算工况 假设拉索C10发生断丝损伤,截面削弱50%(即损伤索有50%的钢丝或钢绞线断裂,已断裂的钢丝或钢绞线不再受力),采用面积折减法、弹模折减法、反向荷载法和实体单元法模拟拉索损伤,分析全桥索力及主梁挠度的变化规律。4种损伤模拟方法的计算结果如图5和图6所示。图中索力变化率=(拉索损伤后的索力-成桥索力)/成桥索力×100%,挠度变化值=拉索损伤后的挠度值-成桥预拱度。 图5 C10损伤50%后索力变化率 图6 C10损伤50%后主梁挠度变化分布曲线 从图5可以看出:采用面积折减法、弹模折减法和实体单元模拟法3种方法得到的索力变化率相近;断丝50%的情况下损伤索的索力下降接近50%,而与损伤索位于索塔同侧的其他拉索的索力略有提高,并且离损伤索越近者索力增大的百分比越大,而位于索塔另一侧的拉索索力变化很小;采用反向荷载法得到的结果与采用其他3种方法得到的结果偏差较大。 从图6可以看出:4种损伤模拟方法下得到的主梁挠度变化分布曲线的分布规律基本一致;损伤索所在侧梁体的挠度较大(并且损伤索锚固点对应的梁体挠度最大),而索塔另一侧梁体的挠度较小;反向荷载法的计算结果与其他3种方法的结果偏差较大。面积折减法、弹模折减法和实体单元法3种方法得到的各拉索索力变化率分布规律及主梁挠度变化分布规律与文献[2]和文献[4]的结果一致。 在这4种损伤模拟方法中,反向荷载法的计算结果偏差较大(原因可能是因为它无法考虑拉索垂度效应的影响,并且所加的反向荷载是由损伤前拉索的应力求得并且保持不变,这与实际情况不符);实体单元法建模过程较为复杂;若假设拉索的损伤是拉索刚度系数的改变,则弹模折减法与面积折减法等价;面积折减法的概念明确,操作简单。 4.2.1不同长度范围损伤模拟结果对比 采用实体单元法模拟局部损伤,假设拉索C6,C8,C10和C12分别发生锈蚀损伤,截面被削弱50%(但未发生断丝情况)。计算时分别单独考虑某根拉索发生锈蚀损伤,截面被削弱程度保持不变,其损伤长度分别为索长的1%,2%,4%,10%,20%,50%和100%共7种情况(损伤起始位置为拉索与梁体的锚固端,如图3所示)。图7和图8分别为C10拉索发生上述程度锈蚀损伤情况时全桥索力变化率和梁体挠度变化分布曲线。其他拉索单独发生锈蚀损伤时,计算结果与图7和图8相类似(略)。图9和图10分别为C6,C8,C10和C12分别发生锈蚀损伤时,损伤索索力变化率随损伤程度不同而变化的对比图和损伤索锚固点对应的梁体挠度随拉索损伤程度而变化的对比图。 图7 C10不同局部损伤程度下索力变化率 图8 C10不同局部损伤程度下主梁挠度变化分布曲线 图9 损伤索的索力变化率随其损伤程度变化曲线 图10各损伤索对应主梁锚固点处梁体的挠度随损伤索损伤程度变化的曲线 从图7和图9可以看出:不同拉索索力的变化趋势相同,拉索局部损伤范围越大,损伤索索力下降越多;当拉索损伤分布的长度范围相对较小时,损伤索的索力下降较少,索力变化率随着损伤长度的增加而增加;当拉索损伤分布的长度范围相对较大时,索力变化率随着损伤长度的增加而增加的速率趋缓,但索力下降依然明显。由图5、图7和图9可以看出,当某拉索各截面在其全长范围内都发生50%的截面削弱时,索力下降量与断丝50%的情况相同(此时采用实体单元法的计算结果与采用面积折减法计算的结果相同,2种损伤模拟方法相互印证)。但是,当拉索局部损伤(截面有所削弱,但未发生断丝)分布范围较小时,索力下降幅度较小,这与采用面积折减法计算的结果差别较大。 从图8和图10可以看出,C6,C8,C10和C12索分别发生局部损伤时,梁体挠度变化值的分布规律基本相同,拉索局部损伤范围越大,损伤索锚点处梁体挠度变化值越大(下挠越厉害);当局部损伤长度较短时,梁体挠度较小,挠度值随损伤长度的增加而增大;当局部损伤范围较大时,随损伤长度的增加,梁体下挠程度趋缓。由图6、图8和图10可以看出,当某拉索各截面在其全长范围内都发生50%的截面削弱时,梁体挠度的变化情况与断丝50%的情况相同(此时采用实体单元法的计算结果与采用面积折减法的计算结果也相同)。但是,当拉索局部损伤(截面有所削弱,但未发生断丝)分布范围较小时,梁体挠度变化幅度较小,这与采用面积折减法计算的结果差别较大。 4.2.2不同程度径向局部损伤模拟结果对比 同样采用实体单元法模拟局部损伤,假设C10拉索仅在中间1 m范围内发生局部损伤,分别考虑不同程度径向损伤,即分别考虑拉索截面发生10%,20%,30%,40%,50%和60%的损伤,但未发生断丝情况。计算结果如图11—图13所示。 图11 C10发生不同程度径向损伤时的索力变化率 图12C10发生不同程度径向损伤时主梁的挠度变化分布曲线 图13C10发生不同程度径向损伤时损伤索最大应力变化曲线 从图11和图12可以看出,拉索仅在小范围(1 m)内发生局部径向损伤时,索力变化率及梁体挠度变化值随损伤程度的增大而增大,但总的变化幅值都比较小。当局部损伤程度小(截面削弱小于40%)时,随损伤程度的增大,索力变化率及梁体挠度变化值缓慢增加;当局部损伤程度较大(面积削弱大于40%)时,随损伤程度的增大,索力变化率及梁体挠度变化值快速增加。 C10索损伤前的张拉控制应力为739.7 MPa,发生这种小范围的局部损伤后会出现应力集中现象。从图13可以看出,拉索发生损伤后,损伤位置的最大局部应力随着损伤程度的增加有快速增加的趋势,当这种损伤达到索面积的50%时,损伤处的最大应力即接近达到索钢材的极限强度。若这种损伤继续发展,很快会出现断丝现象。与损伤向索长度方向发展不同,这种向径向发展的小范围损伤造成索力下降和梁体挠度变化的特点是数值小、前期发展速度慢后期发展速度快,后期的应力集中现象造成的断丝具有“突发”性。若组成索的钢丝或钢绞线大面积出现这种局部损伤,对斜拉桥结构将是非常危险的。 (1)针对斜拉索断丝损伤,采用面积折减法、弹模折减法和实体单元法进行模拟计算,其结果(包括索力变化以及主梁挠度变化规律)基本相同,并与有关文献结果一致。这3种拉索断丝损伤模拟方法中,面积折减法概念明确、操作简单,可作为模拟断丝损伤的首选方法。采用反向荷载法模拟计算的结果与上述3种方法的结果偏差较大,一般不宜采用。用实体单元法既可模拟斜拉索不同长度范围的局部锈蚀损伤,也可模拟斜拉索局部范围内不同锈蚀深度(即不同程度的截面削减)损伤。针对斜拉索局部锈蚀损伤,建议采用实体单元法进行模拟。 (2)针对拉索发生局部损伤(只是局部截面有所削弱,且未发生断丝),宜采用实体单元法进行模拟。当损伤分布长度范围较小时,索力变化率及梁体挠度的变化幅度较小,其数值随着损伤长度的增加而增大;当拉索局部损伤分布长度范围相对较大时,索力变化率及梁体挠度的变化值随损伤长度的增加而增大的趋势趋缓。只有当拉索在其全长范围内发生同样的损伤时,索力变化率及梁体挠度变化值与断丝情况相同。即只有在这种情况下,采用面积折减法或弹模折减法模拟拉索损伤的计算结果与采用实体单元法模拟拉索损伤的计算结果相同。 (3)当斜拉索仅在小范围(如1 m)内发生局部径向损伤(截面削减)时,索力及梁体挠度随损伤程度的增大(截面减小)而增大,但总的变化幅度都比较小。当局部损伤程度较小时,随损伤程度的增大,索力及梁体挠度变化缓慢增加;当局部损伤程度较大时,随损伤程度的增大,索力及梁体挠度变化快速增加。斜拉索发生这种小范围的局部损伤后会伴随出现应力集中现象,损伤发展后期的应力集会造成拉索突发断丝现象。 [1]李延强,赵世英,杜彦良.基于最敏感斜拉索张力指标的斜拉桥主梁损伤识别方法[J].中国铁道科学,2014,35(2):20-25. (LI Yanqiang,ZHAO Shiying,DU Yanliang.Damage Identification Method for the Main Girder of Cable-Stayed Bridge Based on the Tension Indices of the Most Sensitive Stay Cable[J].China Railway Science,2014,35(2):20-25.in Chinese) [2]梁柱,李娜,郑春.基于挠度及索力监测的斜拉索损伤敏感性分析[J].公路,2009(3):40-43. (LIANG Zhu,LI Na,ZHENG Chun.Sensitivity Analysis of Cable Damage Based on Monitoring of Deflection and Cable Tension[J].Highway,2009(3):40-43.in Chinese) [3]张戌社,杜彦良,金秀梅,等.基于光纤光栅的斜拉桥索力在线监测[J].交通运输工程学报,2003,3(4):22-24. (ZHANG Xushe,DU Yanliag,JIN Xiumei,et al.In-Situ Monitoring for Cables’ Tension with Optical Fiber Grating Sensors[J].Journal of Traffic and Transportation Engineering,2003,3(4):22-24.in Chinese) [4]赵玲,李爱群,缪长青,等.大跨斜拉桥的拉索损伤识别[J].桥梁建设,2004(5):19-22. (ZHAO Ling,LI Aiqun,MIAO Changqing,et al.Identification of Damages in Stay Cables of Long-Span Cable-Stayed Bridge[J].Bridge Construction,2004(5):19-22.in Chinese) [5]WANG P H,TSENG T C,YANG C G.Initial Shape of Cable Stayed Bridges[J].Computers and Structures,1993,46(6):1095-1106. [6]李岩,盛洪飞,黄新艺.大跨径斜拉桥动力分析基准有限元模型研究[J].公路交通科技,2006,23(9):58-62. (LI Yan,SHENG Hongfei,HUANG Xinyi.Research on the Baseline Finite Element Model for Dynamic Analysis of Long Span Cable-Stayed Bridges[J].Journal of Highway and Transportation Research and Development,2006,23(9):58-62.in Chinese) [7]李建慧,李爱群,缪长青,等.润扬大桥修正斜拉索力的基准有限元模型[J].东南大学学报:自然科学版,2007,37(2):266-269. (LI Jianhui,LI Aiqun,MIAO Changqing,et al.Baseline FE Model to Revise Cable Tensions in Runyang Cable-Stayed Bridge[J].Journal of South East University:Natural Science Edition,2007,37(2):266-269.in Chinese) [8]王海龙,刘杰,王新敏,等.建立斜拉桥基准有限元模型的新方法与实现[J].振动、测试与诊断,2014,34(3):458-462. (WANG Hailong,LIU Jie,WANG Xinmin,et al.Influence of Stiffness on Random Response of Rotor System[J].Journal of Vibration,Measurement & Diagnosis,2014,34(3):458-462.in Chinese) [9]叶梅新,韩衍群,张敏.基于ANSYS平台的斜拉桥调索方法研究[J].铁道学报,2006,28(4):128-131. (YE Meixin,HAN Yanqun,ZHANG Min.Research on Adjusting Cable Tensions of Cable-Stayed Bridges Based on ANSYS[J].Journal of the China Railway Society,2006,28(4):128-131.in Chinese) [10]叶梅新,韩衍群,张敏.ANSYS二次开发技术在确定斜拉桥初始恒载索力中的应用[J].铁道科学与工程学报,2005,7(3):56-59. (YE Meixin,HAN Yanqun,ZHANG Min.Development and Application of ANSYS in Long-Span Cable-Stayed Bridge[J].Journal of the Railway Science and Engineering,2005,7(3):56-59.in Chinese) [11]周林仁,欧进萍.基于径向基函数响应面方法的大跨度斜拉桥有限元模型修正[J].中国铁道科学,2012,33(3):8-15. (ZHOU Linren,OU Jinping.Finite Element Model Updating of Long-Span Cable-Stayed Bridge Based on the Response Surface Method of Radial Basis Function[J].China Railway Science,2012,33(3):8-15.in Chinese) [12]梁鹏,肖汝诚,张雪松.斜拉桥索力优化实用方法[J].同济大学学报,2003,31(11):1270-1274. (LIANG Peng,XIAO Rucheng,ZHANG Xuesong.Practical Method of Optimization of Cable Tensions for Cable-Stayed Bridges[J].Journal of Tongji University,2003,31(11):1270-1274.in Chinese) [13]黄娟.大跨度预应力混凝土斜拉桥长期荷载作用下时变效应分析[D].广州:华南理工大学,2008. (HUANG Juan.Analysis of Time-Dependent Effects on PC Cable-Stayed under Long-Term Load[D].Guangzhou:South China University of Technology,2008.in Chinese) [14]黄娟,王荣辉.考虑锈蚀影响的拉索状态UL列式分析法[J].公路交通科技,2008,25(12):108-112. (HUANG Juan,WANG Ronghui.UL Formulation Analysis for Corrosion Effect on Cable State[J].Journal of the Highway and Transportation Research and Development,2008,25(12):108-112.in Chinese)2.2 弹模折减法
2.3 反向荷载法
2.4 实体单元法
3 拉索局部损伤的数值模拟方法
3.1 损伤沿长度发展情况
3.2 损伤沿径向发展情况

4 拉索损伤对索力和挠度分布规律的影响
4.1 断丝损伤的影响


4.2 局部损伤的影响



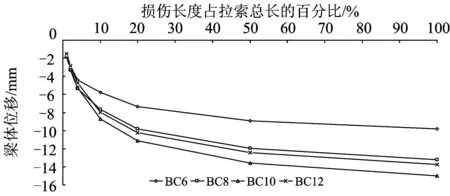
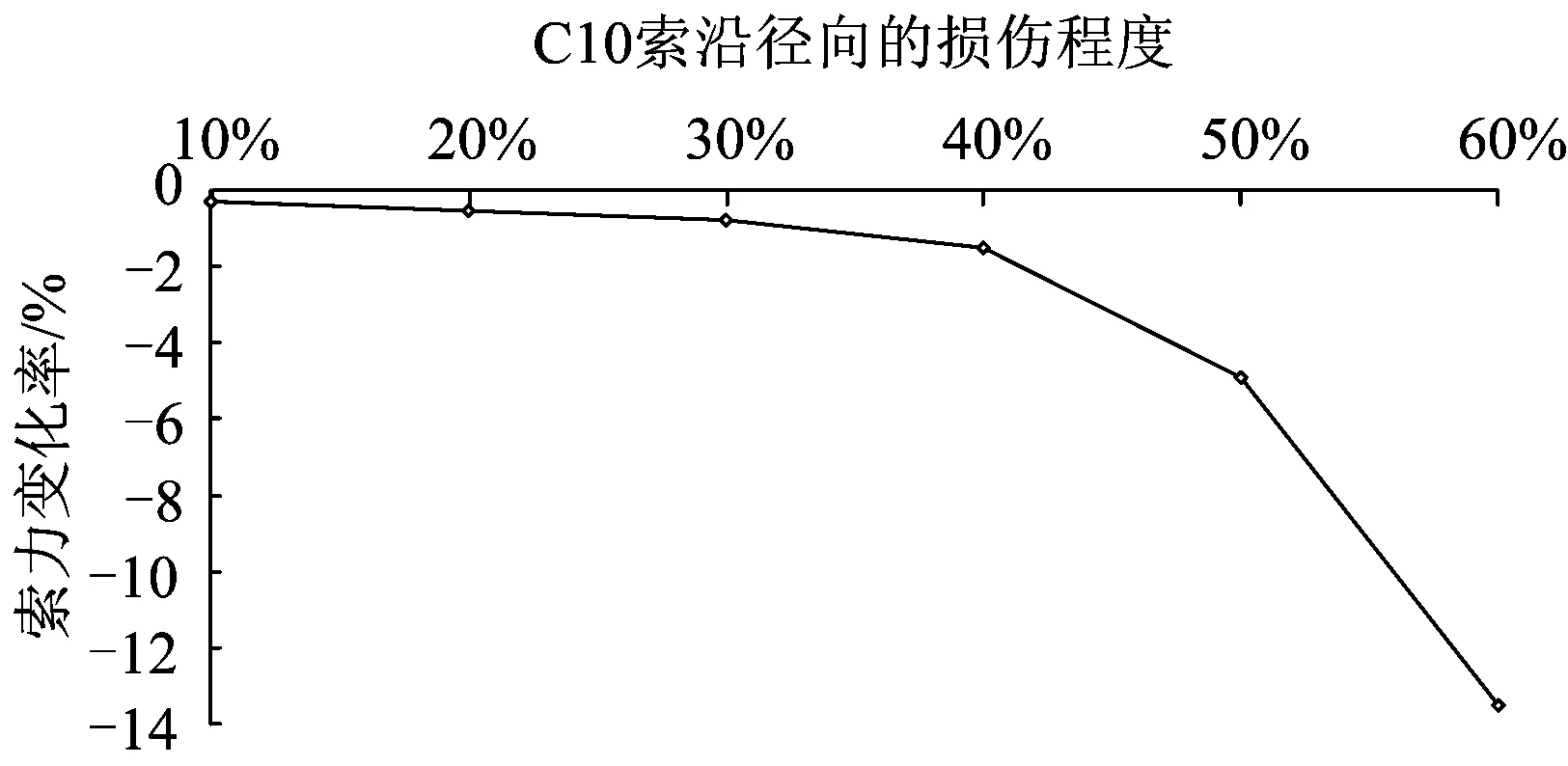
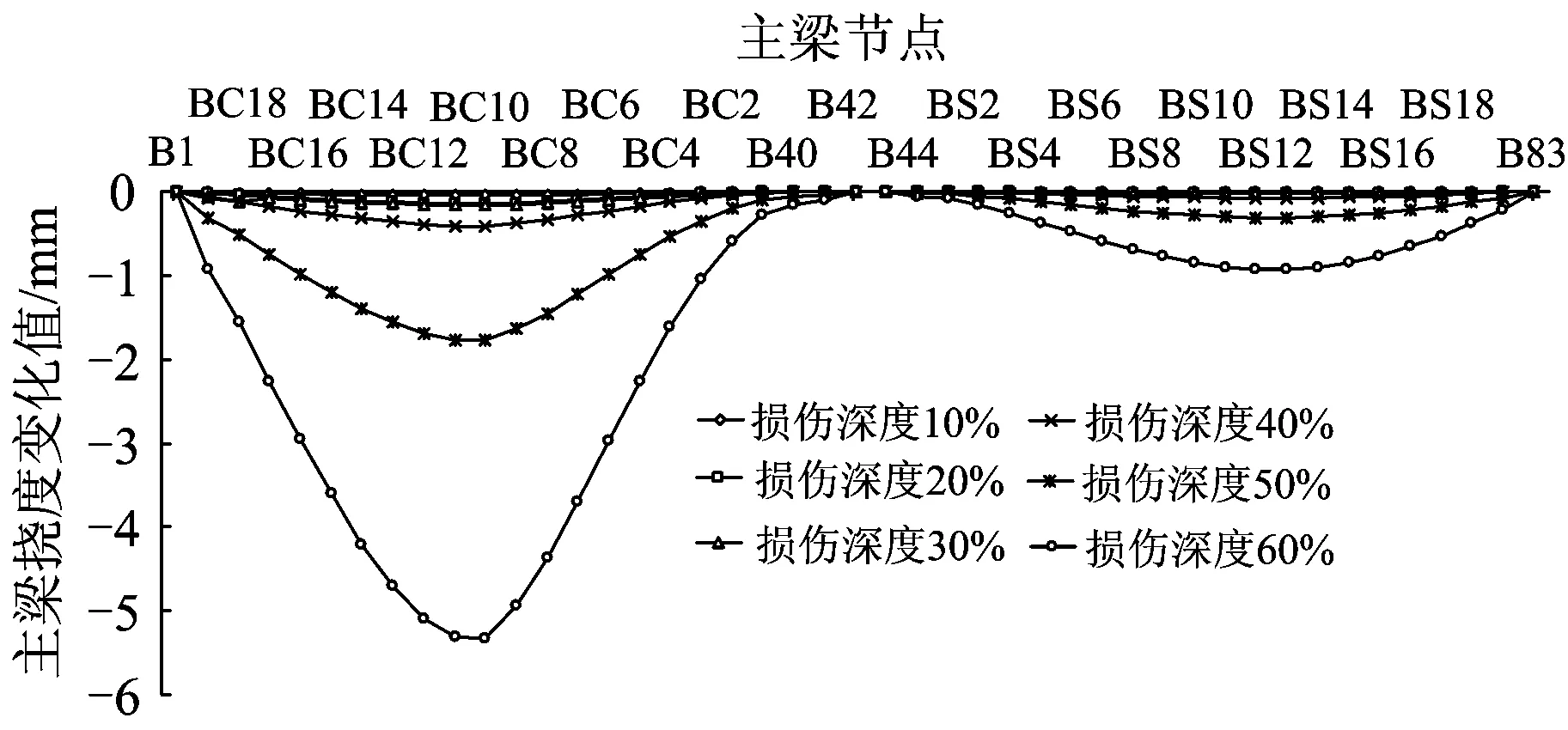

5 结 论
