铁路隧道仰拱及仰拱填充层动力响应分析
2016-04-10杜明庆张顶立张素磊熊磊晋
杜明庆,张顶立,房 倩,张素磊,熊磊晋
(1.北京交通大学 隧道及地下工程教育部工程研究中心,北京 100044;2.青岛理工大学 土木工程学院,山东 青岛 266033)
在铁路隧道运营期间,当隧道仰拱填充层与道床板间产生离缝时,若不能及时发现并作相应处理,在列车循环动荷载的作用下,离缝则有可能迅速增大,导致道床板产生错台裂缝、甚至断裂,直接影响铁路的平顺性和列车的安全运行,因此有必要对仰拱及仰拱填充层在列车动荷载作用下的动力响应规律进行更深入的研究。
既有的对列车动荷载作用下动力响应规律的研究成果中,主要集中在路基、桥基、路桥过渡段。在路基的动力响应研究方面[1-11],Pedro Alves Costa等利用2.5D有限元方法研究了在高速列车动荷载作用下非线性土的动力响应规律;梁波等对高速铁路的振动荷载进行了模拟研究。在桥梁动力响应研究方面,李克飞等[12]对北京地铁5号线高架线减振措施进行了现场测试,比较了钢轨和道床竖直振动加速度的时域和频域;孙璐等[13]对高速铁路CRTSⅡ型板式无砟轨道的结构动力特性进行了分析,建立了无砟轨道结构—下部基础结构动力有限元分析模型,得到了不同列车速度下无砟轨道结构的动力特性。在路桥过渡段动力响应研究方面,王永和等[14]对秦沈铁路客运专线路桥过渡段的路基在高速列车作用下的动应力进行了原位测试,对路桥过渡段线路的纵向动应力分布规律进行了分析。这些研究工作主要针对列车动荷载作用下动应力和振动加速度等指标的分布规律和振动频谱进行了分析,并没有对响应指标的衰减规律做系统全面的研究。李德武等[15]采用弹塑性二维非线性有限元法分析了隧道及周围环境在列车振动下的响应,对仰拱与边墙不同的联结方式、仰拱不同的刚度对列车振动衰减的影响进行了分析,但没有考虑不同运行速度列车的动荷载作用下仰拱的动力响应规律。
本文以兰新第2双线福川铁路隧道为研究对象,在仰拱及仰拱填充层中埋设应力传感器和加速度传感器等,进行现场原位测试,对采集的数据进行统计分析,分析在不同运行速度列车的动荷载作用下,道床板下不同深度处仰拱及仰拱填充层的动应力和振动加速度响应规律,并通过数值模拟对监测结果进行对比分析,以期为类似工程提供借鉴和参考。
1 现场测试
1.1 工程概况
福川铁路隧道位于甘肃省永靖县境内,穿行于湟水河右岸高阶地和低中山区,地层以泥岩为主,局部间夹薄层砂岩,呈紫红、棕红色、局部灰绿色,泥钙质胶结,薄层—中厚层构造,成岩作用较差,节理裂隙较发育,弱风化,属Ⅳ级围岩。隧道为双线隧道,隧道洞身一般埋深为50~180 m,最大埋深约270 m,最小埋深约7 m。隧道内线路纵坡为人字坡。隧道全长10 649 m,最大高度为12.23 m,最大宽度为14.70 m。
衬砌采用Ⅳa—1型,即初期支护喷C25混凝土,拱墙处厚度为250 mm,仰拱处厚度为100 mm;拱墙设φ6钢筋网,间距为200 mm×200 mm;拱墙设置系统锚杆,间距为1 200 mm×1 500mm,长度为3 000 m;拱墙设置Ⅰ18型钢钢架,纵向间距为1 000 mm。二次衬砌为C30素纤维混凝土,拱墙处厚度为450 mm,仰拱处厚度为550 mm,衬砌断面如图1所示。

图1 隧道衬砌断面图(单位:mm)
1.2 测试概况
在隧道内长钢轨铺设完成后进行了小车复测,复测时发现左右轨高程差超限,经过进一步的测量和调查,确认隧道存在轨道上鼓、道床板与仰拱找平层脱离、仰拱开裂等现象,如图2所示。

图2 裂缝分布
发现病害后相关单位立即对其进行了整治,整治仰拱及仰拱填充层用的混凝土为C40。整治过程中将测试元件预埋在混凝土中,在临近仰拱位置时将相应测点移至仰拱的上、下表面。测试元件为电阻应变式压力计、高灵敏度加速度计,另外埋设温度传感器进行温度补偿。电阻应变式压力计埋设在钢轨正下方和轨道中心线正下方,振动加速度计和温度传感器仅埋设在轨道中心线正下方。实测断面选择在DK41+410处,从道床板往下按照200~600 mm不等的间距埋设监测元件,共埋设电阻应变式压力计30只,高灵敏度加速度计10只,温度传感器10只。测试元件的埋设位置如图3所示,埋设现场如图4所示。
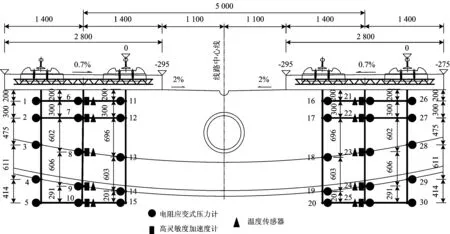
图3 测试元件埋设位置(单位:mm)

图4 测试元件埋设位置及埋设现场
试验列车为CRH5动力分散型电动车组,8辆编组,车辆的转向架固定轴距为2.70 m,最大轴重为17 t,头车长27.60 m,中间车长25.00 m,全长211.50 m。由于某些原因,在列车经过隧道时采取了降速运行的措施,因此,列车运行速度取50,150,200 km·h-1。
2 实测结果分析
取左侧轨道的右边5个监测点的实测数据进行分析,5个监测点的位置分别为道床板下深度0.200,0.500,1.196,1.799,2.000 m,为便于叙述,以下简称为深度0.2,0.5,1.2,1.8,2.0 m。仰拱及仰拱填充层统称为结构。
2.1 不同深度处结构的动应力响应
列车运行速度为200 km·h-1时,在列车动荷载作用下不同深度处结构的动应力响应如图5所示,图5(a)中①—⑧表示列车车厢所在的位置,16个动应力峰值分别代表车厢前后轮经过测试断面时仰拱的动应力响应。由图5可知:随着列车轮对的通过,结构的动应力响应出现周期性的峰值;随着深度的增加动应力逐渐减小,深度为0.2,0.5,1.2,1.8,2.0 m处,动应力峰值分别为52,39,26,20,17 kPa。
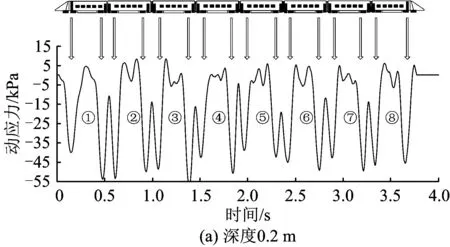




图5 不同深度处结构的动应力响应时程曲线
2.2 不同列车运行速度下的动应力响应
列车运行速度为50和150 km·h-1时列车动荷载作用下深度0.2 m处结构的动应力响应如图6所示(列车运行速度为200 km·h-1时的见图5(a))。

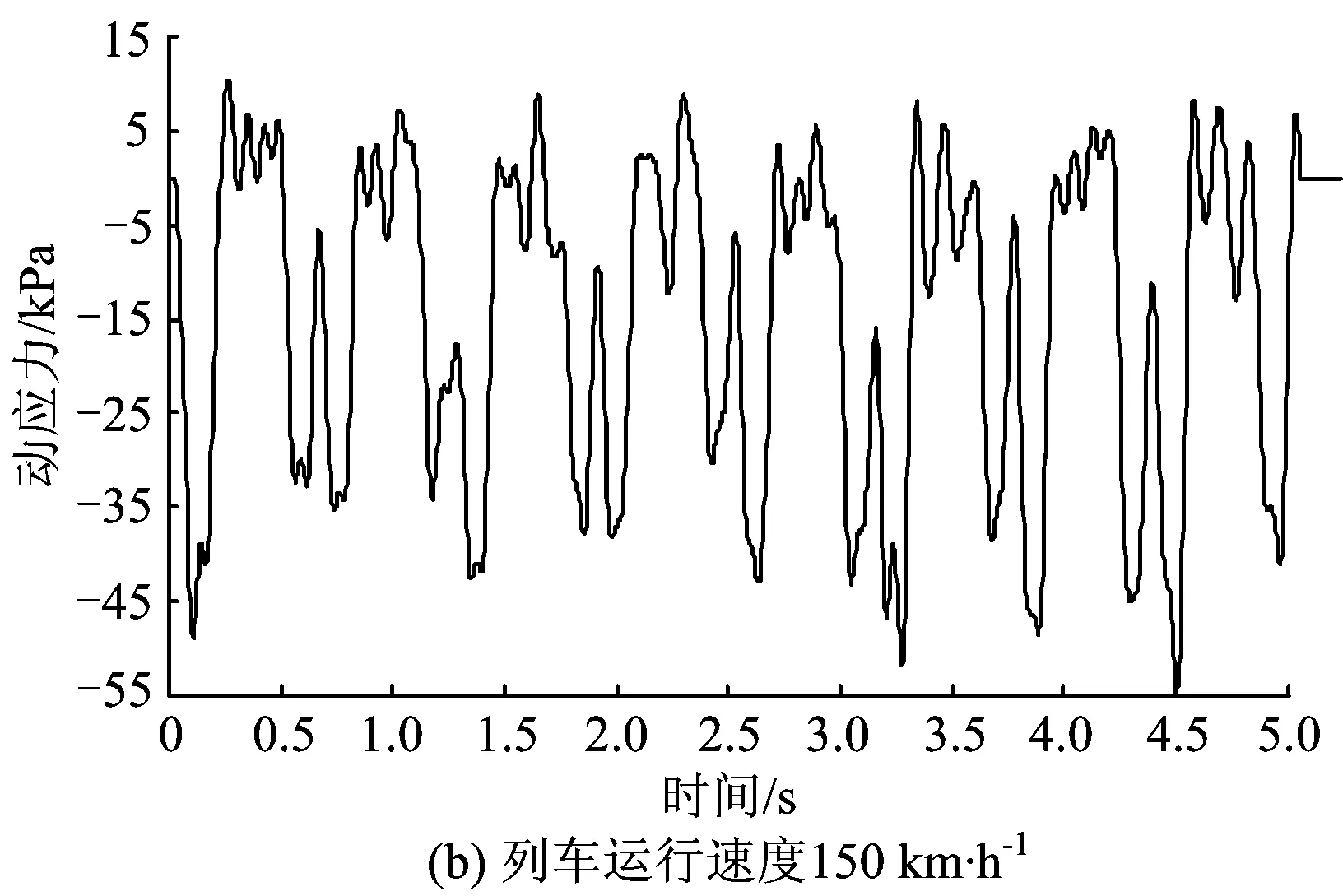
图6列车运行速度分别为50和150 km·h-1时结构的动应力响应时程曲线
由图5(a)和图6可知:随着列车的通过,结构的动应力响应出现周期性的峰值;随着列车运行速度的提高动应力逐渐增大,列车运行速度为200,150,50 km·h-1时,动应力峰值分别为52,44,38 kPa。
2.3 不同列车运行速度时不同深度处结构的动应力响应
不同列车运行速度时不同深度处结构的动应力响应如图7所示。由图7可知,列车运行速度对动应力的影响随着深度的增加而减小。说明仰拱及仰拱填充层承受了大部分的动应力,因此,应将其作为结构设计的重点。

图7不同列车运行速度时不同深度处结构动应力响应曲线
以列车运行速度为200 km·h-1时深度0.2 m处结构的动应力为基准,取其值为1,则不同列车运行速度时不同深度处结构动应力的衰减幅度见表1。由表1可知:列车运行速度为200 km·h-1条件下,深度为2.0 m时比深度为0.2时的动应力衰减幅度达67%;深度为0.2 m条件下,列车运行速度为50 km·h-1时比200 km·h-1时动应力衰减幅度达27%。
定义h为深度;f1,f2,f3分别代表列车运行速度为50,150,200 km·h-1时结构的动应力。对实测数据进行拟合,可得不同列车运行速度时结构动应力与深度(0.2~2.0 m范围内)关系的拟合公式,见表2。该拟合公式可用于对类似地层和工况下结构的动应力响应进行计算。

表1 动应力衰减幅度
表2不同列车运行速度时动应力与深度关系的拟合公式和相关系数

列车运行速度/(km·h-1)结果动应力与深度关系的回归方程相关系数50f1=-13681h3+51521h2-67184h+489400996150f2=-15292h3+59320h2-79422h+574670994200f3=-9505h3+38958h2-63069h+630200999
2.4 竖向振动加速度响应分析
列车运行速度为200 km·h-1时,在列车动荷载作用下不同深度处结构的竖向振动加速度响应如图8所示(需要说明的是,由于监测环境比较恶劣,在深度为0.2,1.2 m处没有测得竖向振动加速度有效值),图中正值表示与重力加速度方向相同,负值表示与重力加速度方向相反。由图8可知:随着列车轮对的通过,竖向振动加速度出现周期性峰值;随着深度的增加竖向振动加速度响应幅值逐渐降低,深度为0.5,1.8,2.0 m时,竖向振动加速度响应幅值分别为0.735,0.490,0.435 m·s-2;同理,将深度为0.5 m处的竖向振动加速度幅值作为基准,则在深度为1.8,2.0 m处,竖向振动加速度已衰减33%和41%。

图8 不同深度处结构竖向振动加速度的时程曲线
不同列车运行速度时不同深度处竖向振动加速度响应如图9所示。由图9可知:竖向振动加速度响应随着列车运行速度的增大而增大,竖向振动加速度的衰减速度随着深度的增加而逐渐减小。在深度为0.5 m处,列车运行速度为50 km·h-1时比200 km·h-1时的振动加速度衰减70%。

图9不同列车运行速度时不同深度处结构竖向振动加速度响应曲线
将该结果与文献[16]中路基的竖向振动加速度响应相比,隧道仰拱中竖向振动加速度的响应相对较小,这主要是因为上部衬砌与仰拱已连成一体,对仰拱的振动起到了一定的缓解作用。
3 数值模拟分析
为进一步了解铁路隧道仰拱及仰拱填充层的动力响应规律,基于有限元软件ABAQUS对动荷载作用下仰拱及仰拱填充层在不同列车运行速度、不同混凝土强度、不同混凝土厚度下的动力响应规律进行数值分析。
3.1 系统运动方程
将运行列车简化为作用在轨道上的移动荷载。列车动荷载作用下隧道仰拱结构的运动方程表达式[17]为

(1)

模拟中采用Rayleigh线性组合法,该组合法假定体系的阻尼矩阵为质量矩阵和刚度矩阵的线性组合,即
C=αM+βK
(2)
其中,
(3)
(4)
式中:α和β为常数;ε和ω分别为振型对应的阻尼比和自振圆频率;i,j=1,2,3,…。
3.2 几何模型及材料参数
测试断面处隧道的埋深为190 m,宽度为14.70 m,高度为12.23 m;仰拱厚度为0.55 m,仰拱填充层厚度为1.25 m;道床板的宽度为2.80 m,高度约为0.29 m。几何模型长×宽×高分别为100 m×25 m×100 m。选用ABAQUS软件进行计算,以荷载的形式补偿隧道模型埋深的不足[18],模型采用黏弹性人工边界条件,几何模型的局部放大图如图10所示。

图10 模型局部放大图
隧道穿越地层主要以泥岩为主,故模型中土层只考虑了泥岩1种土层,各材料的物理力学参数取值见表3。仰拱填充层和道床板混凝土采用C30,混凝土阻尼比为0.02;泥岩的黏聚力为110 kPa,内摩擦角为25°。列车运行速度取200 km·h-1。深度取0.2,0.5,1.2,1.8,2.0 m。计算前首先进行模态分析,根据模态分析的结果,利用式(3)和式(4)可计算Rayleigh阻尼系数。

表3 材料的物理力学参数
3.3 实测结果与模拟结果对比分析
3.3.1不同列车运行速度时不同深度处结构的动应力响应
列车运行速度分别取50,100,150,200,250 km·h-1,则动应力响应的模拟结果与现场实测结果对比如图11所示。模拟的与实测的列车运行速度为200 km·h-1时深度0.2 m处的动应力响应时程曲线对比如图12所示。由图11和图12可知:模拟结果的波动幅度和频率与实测结果基本吻合。这也进一步证明了仰拱及仰拱填充层是承载动应力的主要载体,应作为结构设计的重点。
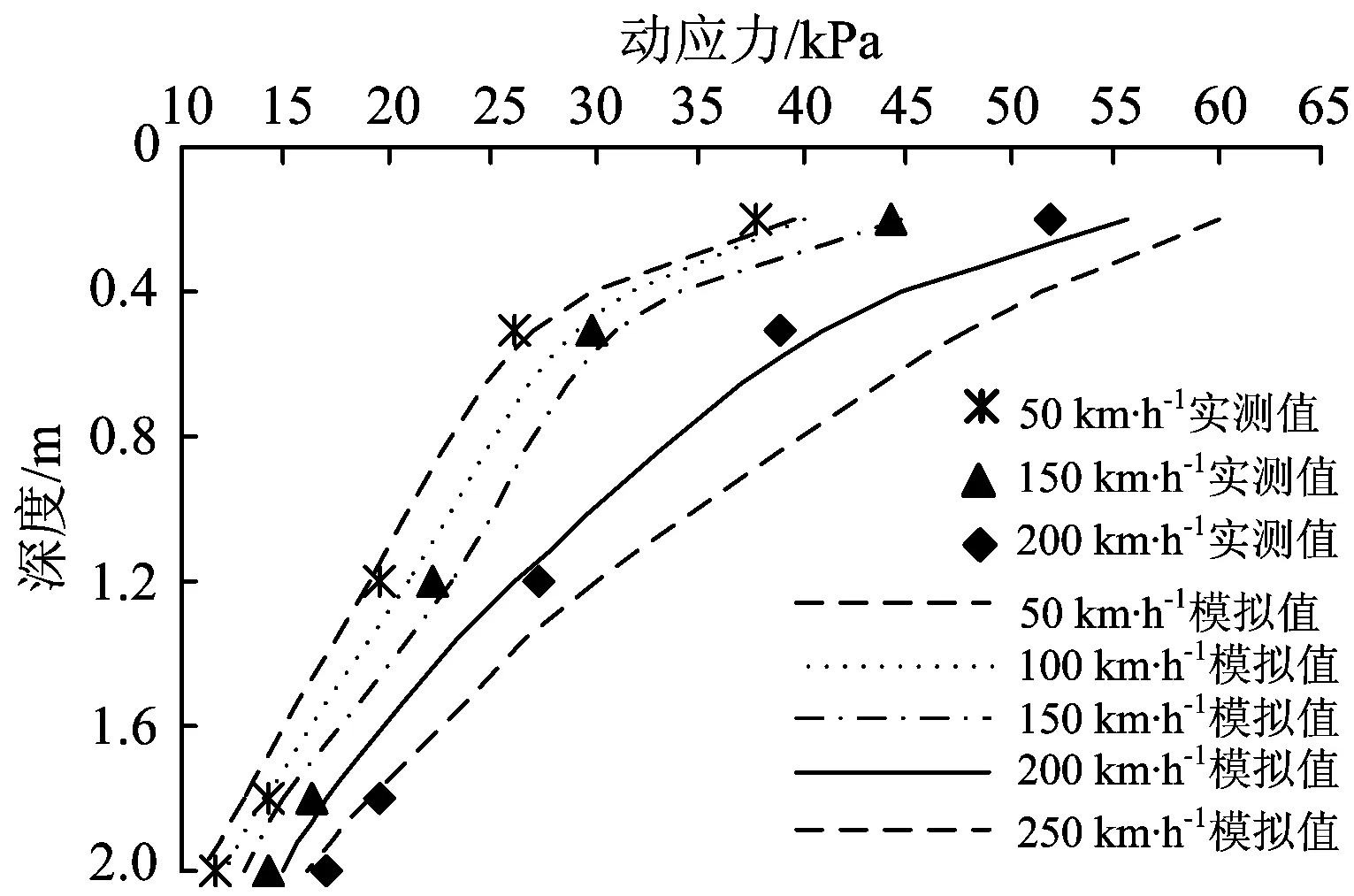
图11不同列车运行速度时不同深度处结构动应力响应曲线
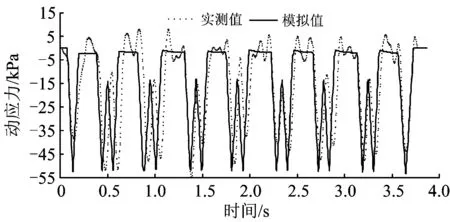
图12 动应力响应时程曲线对比
3.3.2不同混凝土强度时结构的动应力响应
仰拱及仰拱填充层的混凝土标号分别取C20,C25,C30,C40,C50,模拟得到的不同混凝土强度时不同深度处结构动应力响应曲线如图13所示。

图13不同混凝土强度时不同深度处结构动应力响应曲线
由图13可知:随着混凝土强度的增加,相同深度处的动应力幅值减小,但减小幅度相对有限,如深度0.2 m处,混凝土标号为C20时动应力为60 kPa,混凝土标号为C50时动应力为54 kPa,减小幅度仅为10%,可见仰拱及仰拱填充层的混凝土强度的增加对其动应力衰减幅度的影响相对有限,故在设计仰拱及仰拱填充层时,应综合考虑动应力响应及经济因素,选取合适强度的混凝土。
4 结 论
(1)列车运行速度一定时,结构的实测动应力和竖向振动加速度响应均随着道床板下深度的增加而减小。列车运行速度为200 km·h-1时,深度0.2 m处比深度2 m处的动应力衰减67%,深度0.5 m处比深度2 m处的振动加速度衰减41%。
(2)同一深度处,实测动应力和竖向振动加速度响应均随着列车运行速度的降低而减小。深度为0.2 m处,列车运行速度为50 km·h-1时比200 km·h-1时动应力衰减27%;深度为0.5 m处,列车运行速度为50 km·h-1时比200 km·h-1时振动加速度衰减41%。
(3)列车运行速度对动应力和竖向振动加速度的影响均随着深度的增加而减小,因此仰拱及仰拱填充层是承载动应力的主要载体,应作为结构设计的重点。
(4)与路基中的振动加速度响应相比,仰拱中的响应相对较小,主要是因为仰拱与衬砌形成了整体结构,在一定程度上减缓了仰拱的振动。
(5)模拟得到的动应力和竖向振动加速度的波动幅度和频率与实测结果基本吻合,进一步证明了仰拱及仰拱填充层是承载动应力的主要载体。随着仰拱及仰拱填充层混凝土强度的增大,相同深度处的动应力减小,但减小幅度相对有限,因此在实际工程中应综合考虑动应力响应和经济因素,合理选取仰拱及仰拱填充层的混凝土强度。
[1]聂志红,李亮,刘宝琛,等.秦沈客运专线路基振动测试分析[J].岩石力学与工程学报,2005,24(6): 1067-1071.
(NIE Zhihong,LI Liang, LIU Baochen,et al. Testing and Analysis on Vibration of Subgrade for Qinhuangdao-Shenyang Railway[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(6): 1067-1071.in Chinese)
[2]詹永祥,蒋关鲁.无碴轨道路基基床动力特性的研究[J].岩土力学,2010,31(2):392-396.
(ZHAN Yongxiang,JIANG Guanlu. Study of Dynamic Characteristics of Soil Subgrade Bed for Ballastless Track[J].Rock and Soil Mechanics,2010,31(2): 392-396. in Chinese)
[3]高广运,李志毅,冯世进,等.秦—沈铁路列车运行引起的地面振动实测与分析[J].岩土力学,2007,28(9): 1817-1822,1827.
(GAO Guangyun,LI Zhiyi,FENG Shijin,et al. Experimental Results and Numerical Predictions of Ground Vibration Induced by High-Speed Train Running on Qin-Shen Railway[J]. Rock and Soil Mechanics,2007,28(9): 1817-1822,1827.in Chinese)
[4]王常晶,陈云敏.列车荷载在地基中引起的应力响应分析[J].岩石力学与工程学报,2005,24(7): 1178-1186.
(WANG Changjing,CHEN Yunmin. Analysis of Stresses in Train-Induced Ground[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(7):1178-1186.in Chinese)
[5]黄晶,罗强,李佳,等.车辆轴载作用下无砟轨道路基面动应力分布规律探讨[J].铁道学报,2010,32(2): 60-65.
(HUANG Jing,LUO Qiang,LI Jia,et al. Analysis on Distribution of Dynamic Stresses of Ballastless Track Subgrade Surface under Axle Loading of Vehicle [J]. Journal of the China Railway Society,2010,32(2): 60-65. in Chinese)
[6]COSTA P A,CALÇDA R,CARDOSO A S. Track-Ground Vibrations Induced by Railway Traffic: In-Situ Measurements and Validation of a 2.5D FEM-BEM Model [J]. Soil Dynamics and Earthquake Engineering, 2012,32 (1):111-128.
[7]COSTA P A,RUI C,CARDOSO A S, et al. Influence of Soil Non-Linearity on the Dynamic Response of High-Speed Railway Tracks [J]. Soil Dynamics and Earthquake Engineering,2010,30 (4):221-235.
[8]梁波,罗红,孙常新,等.高速铁路振动荷载的模拟研究[J].铁道学报,2006,28(4):89-94.
(LIANG Bo,LUO Hong,SUN Changxin,et al. Simulated Study on Vibration Load of High Speed Railway[J]. Journal of the China Railway Society,2006,28(4):89-94.in Chinese)
[9]陈功奇. 基于现场测试的列车引起地基振动分析[J]. 岩石力学与工程学报, 2015,34(3):601-611.
(CHEN Gongqi. Ground Vibration Analysis Induced by High-Speed Train Based on In-Situ Data[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3):601-611. in Chinese)
[10]白冰, 李春峰. 地铁列车振动作用下近距离平行隧道的弹塑性动力响应[J]. 岩土力学, 2009,30(1):123-128.
(BAI Bing,LI Chunfeng. Elastoplastic Dynamic Responses of Close Parallel Metro Tunnels to Vibration Loading[J]. Rock and Soil Mechanics, 2009, 30(1):123-128. in Chinese)
[11]翟婉明,王少林. 桥梁结构刚度对高速列车—轨道—桥梁耦合系统动力特性的影响[J]. 中国铁道科学,2012,33(1):19-26.
(ZHAI Wanming,WANG Shaolin. Influence of Bridge Structure Stiffness on the Dynamic Performance of High-Speed Train-Track-Bridge Coupled System[J]. China Railway Science, 2012, 33(1):19-26. in Chinese)
[12]李克飞,刘维宁,孙晓静,等.北京地铁5号线高架线减振措施现场测试与分析[J].中国铁道科学,2009,30(4): 25-29.
(LI Kefei,LIU Weining,SUN Xiaojing,et al. In-Situ Test and Analysis on the Vibration Mitigation Measures of the Elevated Line in Beijing Metro Line 5[J]. China Railway Science,2009,30(4): 25-29.in Chinese)
[13]孙璐,段雨芬,赵磊,等.高速铁路CRTSⅡ型板式无砟轨道结构动力特性分析[J].东南大学学报:自然科学版,2014,44(2):406-412.
(SUN Lu,DUAN Yufen,ZHAO Lei, et al. Dynamic Response Analysis of CRTS Ⅱ Ballastless Track Structure of High-Speed Railway[J].Journal of Southeast University:Natural Science Edition,2014,44(2):406-412.in Chinese)
[14]律文田,王永和.秦沈客运专线路桥过渡段路基动应力测试分析[J].岩石力学与工程学报,2004,23(3):500-504.
(LÜ Wentian,WANG Yonghe. Dynamic Stress Analysis of Subgrade-Bridge Transition Section of Qinshen Railway[J]. Chinese Journal of Rock Mechanics and Engineering,2004, 23(3) : 500-504.in Chinese)
[15]李德武,高峰,韩文峰.列车振动下隧道基底合理结构型式的研究[J].岩石力学与工程学报,2004,23(13):2292-2297.
(LI Dewu,GAO Feng,HAN Wenfeng. Study on Rational Structure of Railway Tunnel Bed under Dynamic Vibration Load[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(13):2292-2297. in Chinese)
[16]屈畅姿,王永和,魏丽敏,等.武广高速铁路路基振动现场测试与分析[J].岩土力学,2012,33(5):1451-1456.
(QU Changzi,WANG Yonghe,WEI Limin,et al. In-Situ Test and Analysis of Vibration of Subgrade for Wuhan-Guangzhou High-Speed Railway[J].Rock and Soil Mechanics,2012,33(5):1451-1456.in Chinese)
[17]潘昌实.隧道力学数值方法[M].北京:中国铁道出版社,1995.
[18]庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.
