基于谐波平衡识别法的铁路路基连续压实指标研究
2016-04-10聂志红
聂志红,焦 倓,王 翔
(1.中南大学 土木工程学院,湖南 长沙 410075;2.香港大学 土木工程系,香港)
连续压实控制技术基于压路机—土系统动力学模型,通过对压实过程中振动轮的加速度信号进行实时分析,得到土体的压实指标值。与传统抽样“点测法”相比,连续压实控制技术具有压实状态实时显示、全过程压实质量监控等优点[1],近年来,在铁路路基中得到了逐步应用[2]。
由于压实指标直接反映路基的压实质量,因此是连续压实控制技术的重要研究内容。Geodynamik首先提出了基于振动轮参数(即轮半径和质量)和施工参数(即振动频率、振幅以及速度)的无量纲压实参数CMV的概念,Sandstöm通过试验,分析了振动轮加速度信号的一阶谐波含量与土体压实程度的关系,确定了CMV的计算方法并验证了其适用性[3]。但由于CMV指标仅包含振动轮加速度信号的一阶谐波,当振动轮加速度的谐波成分较多时,其可靠度较低[3]。Sakai对CMV指标进行改进,提出了包含振动轮加速度次谐波和三阶谐波的CCV指标[3,4]。Bomag和Kröber基于压路机—土动力模型,将压路机在2个连续振动周期内传递到土体的能量ω定义为指标,且ω值随着土体压实密实程度的增加而减小[5]。Caterpillar基于Bekker的车辆—变形理论,提出反映土体压实状态的MDP指标,且MDP是一个仅与压实土体性质有关的量[6]。Bomag基于压路机—土动力学模型,提出利用压路机—土接触力和振动轮竖向位移关系曲线的割线模量Evib反映土体的压实状态。Ammann根据压路机—土接触力和振动轮竖向位移曲线,将振动轮最大位移对应的接触力与最大位移的比值k定义为指标[7]。Mooney等根据振动轮加速度信号的频谱提出用总谐波失真指标THD评价土体的压实质量,但由于此指标对路基填料类型以及下卧土层的情况非常敏感,其适用性有待进一步验证[8]。
上述指标中,CMV与CCV指标考虑了振动轮加速度的低阶谐波;MDP,ω,Evib和k指标考虑了压路机—土动力学模型与振动轮加速度时域信号。但这些指标均未综合考虑压路机—土动力学模型与振动轮加速度信号的高阶谐波。文献[9]指出,当路基土体参数中的刚度、阻尼已知时,路基压实状态则也为已知。基于此思路,本文在综合考虑压路机的振动轮加速度信号的高阶谐波和压路机—土动力模型的基础上,引入谐波平衡识别法识别土体参数[10], 进行铁路路基连续压实指标的研究。
1 振动压路机—土的动力模型
在识别压实土体参数时,首先需选定符合路基土体压实状态的振动压路机—土动力学模型。国内外许多学者通过大量的仿真实验以及现场试验研究[11-13],提出了图1和图2所示的符合实际土体压实状态的振动压路机—土动力模型及受力分析图。图中:mf和md分别为压路机机架和振动轮的等效质量;ms为随动土体质量;xf,xd和xs分别为机架、振动轮以及土体的位移;k1,ks分别为减振器和土体的刚度;c1,cs分别为减振器和土体的阻尼;ω为激振器的角速度;FD为激振力;F0为偏心块产生的激振力幅值;Fs为轮—土接触力。
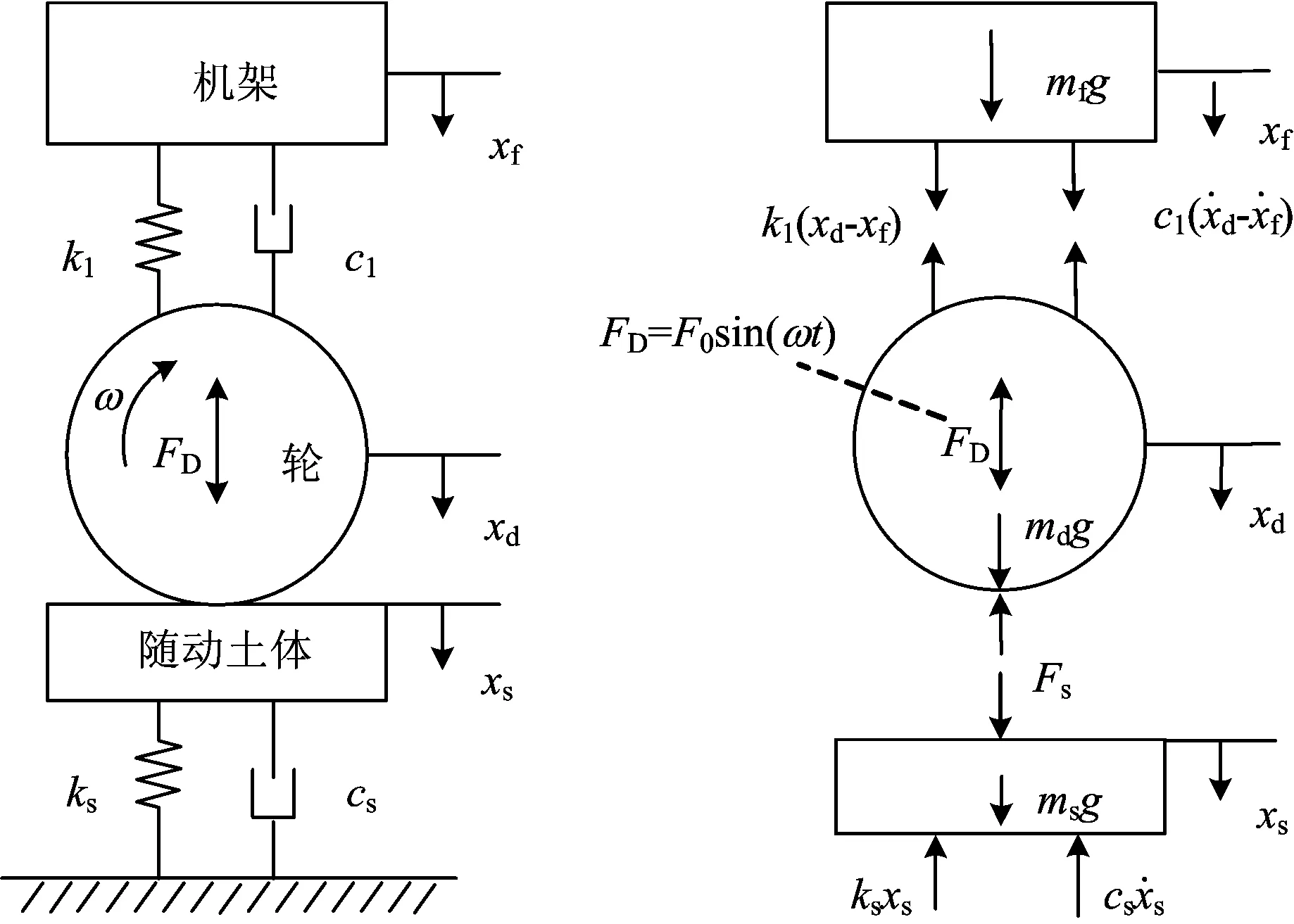
图1压路机—土动力模型图2压路机—土动力模型受力分析
以图1中模型的静平衡位置为坐标原点,基于图2受力分析关系建立动力方程
(1)
当压路机为接地工况[11,13],即xd=xs,Fs>0时,所得振动轮加速度信号是压路机与土作用的结果。而当压路机为非接地工况时(振动轮与土分离),所得振动轮加速度信号不是压路机与土相互作用的结果,为保证识别结果的精确性,本文只考虑接地工况时的情况,此时式(1)可化简为
(2)
其中,
2 压实土体参数识别过程
2.1 识别方程建立
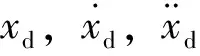
(3)
(4)
式中:uqk,vqk和wqk分别为振动轮和机架的位移、速度、加速度的第k阶傅里叶系数;dk为激振力的第k阶傅里叶系数。
振动轮加速度及F0sin(ωt)的傅里叶系数wdk,dk的计算式如下:
(5)
(6)
由于压实质量连续检测系统采用加速度计,可实时获取振动轮加速度信号,故振动轮、机架的位移与速度的傅里叶系数uqk和vqk可由加速度的傅里叶系数wqk推导得到
(7)
将式(3)—式(7)代入式(2),可得
(8)
根据压路机—土系统响应各阶谐波平衡原理[14],即任意阶谐波下压路机—土动力方程的傅里叶展开式均成立,可建立压实土体参数的识别方程
(9)
上式又可简写为
(10)
2.2 土体参数识别
在由机架谐波平衡方程和振动轮谐波平衡方程所组成的方程组之间存在耦合,因而必须采用多维最小二乘法来识别c1,k1和土体刚度ks、阻尼cs,具体推导过程如下。
(11)
式中:εk为误差矩阵;ε1和ε2分别为机架和振动轮的误差。
上式的误差平方和为
(12)
对式(12)求偏导得
(13)
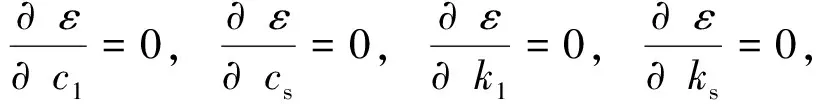
3 仿真试验
应用编制的土体参数识别程序进行仿真试验。
3.1 参数选取
为模拟压路机现场压实工况,mf,md,ω和F0采用龙工LG520A型号压路机的实际施工数据。为了使仿真更加接近实际工况,模型中土体的刚度ks及阻尼cs根据半无限弹性锥模型进行计算[15],即
(14)
(15)
式中:G为土体最大剪切模量;γ为土体泊松比;a为振动轮宽度的一半;b为接地印痕宽度的一半;φ为土体含水率;ρd为土体密度。
上式中各参数值根据文献[13]选取。最终确定的动力模型参数汇总于表1。

表1 动力模型参数取值
3.2 识别结果分析
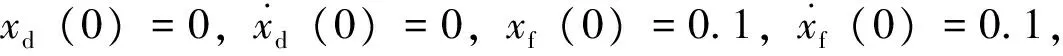
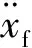

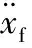

表2 动力模型参数识别结果
由表2可见,各识别结果误差大多随着谐波数的增加而递减,各谐波对应的误差均在5%以内且谐波数为100时的识别误差均不超过3%。为进一步验证识别程序所识别参数的精度,将识别误差最大(谐波数为5)时的识别结果代入原动力方程中进行仿真,得到识别后的轮—土系统的加速度信号,如图4所示。

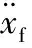
由图4可看出,识别后的加速度信号与图3中的原始加速度信号非常相似。为了进一步分析2个图信号的相似性,须做相图进行对比[16]。识别系统与真实压路机—土系统在1个周期内的相图,如图5—图8所示。
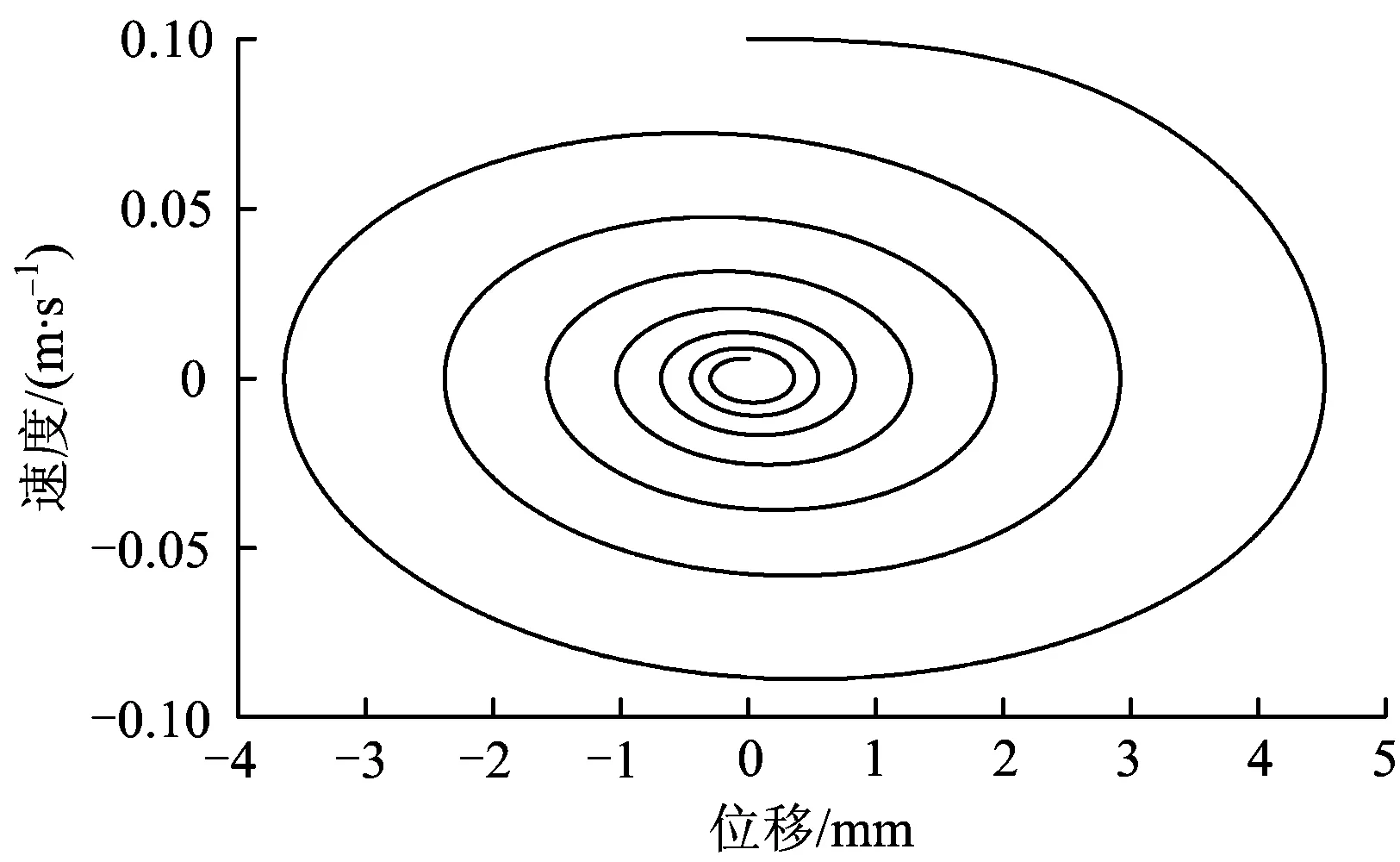
图5 原始值所得机架响应相图
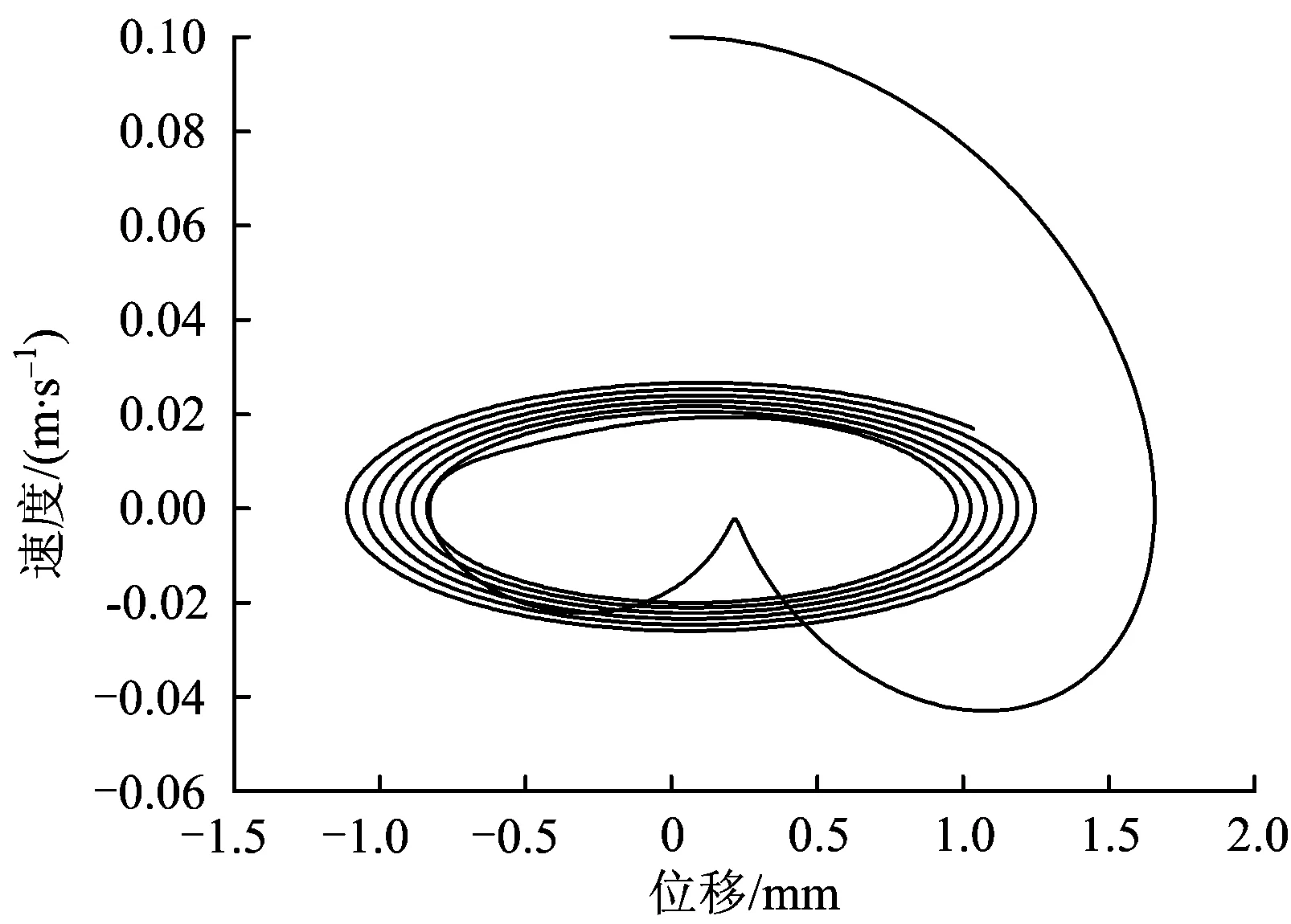
图6 原始值所得振动轮相图
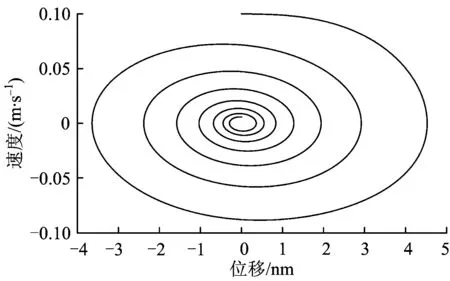
图7 识别值所得机架响应相图
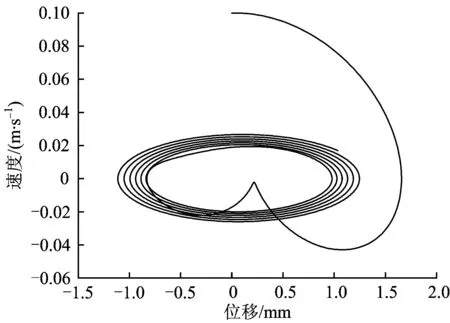
图8 识别值所得振动轮相图
从图5—图8可看出,原始值和识别值所得的相图几乎完全相似。根据以上相图求得相似度矩阵[17],对比识别解与真实解的相似程度,具体比较结果见表3。

表3 机架、振动轮加速度真实解与识别解的相似度
由表3可知,振动轮加速度真实解与识别解的相似度为0.994 5,非常接近1,说明利用识别的土体参数得到的振动轮加速度信号与原加速度信号非常相似。从表3还可看出,图6与图8的振动轮相图的相似度为0.996 2,进一步说明根据识别参数求解得到的振动轮响应与真实值对应的响应非常相近,识别结果可近似看作真实值。
3.3 抗干扰分析
3.3.1高斯噪声
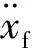
(16)
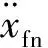
实际检测过程中,噪声功率会随着测量环境和传感器以及设备参数变化,故此处采用原信号在3种不同高斯噪声功率(0.010,0.025,0.050)下的含噪声信号进行参数识别,检验基于谐波平衡识别法的抗干扰性能。
3.3.2抗噪结果分析

表4 不同噪声功率下系统参数识别结果及相似度
从识别结果可以看出,ks,cs,kl和cl的识别值均非常接近原始值,且各参数的识别误差均随着噪声功率的减小而递减。其中,土体参数ks和cs的识别结果在3种噪声功率下的误差均小于5%,说明谐波平衡(HB)识别法具有较强的抗干扰性,识别值可用来反映土体的压实状态。
综上,谐波平衡(HB)识别法在一定噪声功率范围内具有精确的识别结果,能够识别连续压实过程中的土体参数。
4 现场试验
4.1 试验概况
为验证基于谐波平衡识别法在实际压实作业中的可行性,在西成高速铁路陕西西安路基段进行压实试验。试验段里程为DK24+970—DK25+081,使用A组填料,填料基本性质见表5。

表5 填料物理指标
振动轮加速度传感器采用HCF400无线多功能智能传感器,且该传感器在试验前已进行了校核。试验用压路机型号为中联重科YZK25,连续压实检测设备采用美国天宝公司(Trimble)的CCS900—CMV系统,其压实指标为CMV,计算式为
(17)
式中:c为常数;A1为振动轮加速度的一次谐波振幅;A0为振动轮加速度基频振幅[18]。
现场试验设备的具体安装如图9所示,为了保证采集数据的准确性,CCS900—CMV系统传感器与振动轮上的HCF400无线传感器均位于同一竖向位置,且HCF400无线传感器设置为仅测量竖向加速度。

图9 现场试验设备安装图
4.2 试验结果与分析
4.2.1加速度信号预处理
由于压路机工作过程中的压实信号含有噪声信号和奇异点,故在进行振动轮加速度信号分析前,需对其进行预处理。相关学者通过研究压路机振动轮加速度的特点,提出在分析振动轮加速度信号前应对振动轮加速度信号进行信号去噪和奇异点检测[19];同时,文献[19]通过对比FFT去噪和小波去噪结果,验证了小波去噪比FFT去噪具有更高的精度。基于此,本文对振动轮加速度信号进行小波去噪和奇异点检测2项预处理。
在进行小波去噪和奇异点检测前,先对原始振动轮加速度信号进行FFT变换,分析信号的频谱,原始信号的频谱分析结果如图10所示。
由图10可以看出,信号的主要能量集中在低频部分,故在滤波时只需要设置1个上限频率为50 Hz的低通滤波器即可,且在进行小波去噪和奇异点检测时,使用db3小波4层分解检测信号[19]。
图11给出了预处理前后的部分加速度信号。由图11可以看出,经过小波去噪和奇异点检测后的加速度信号更加平滑。
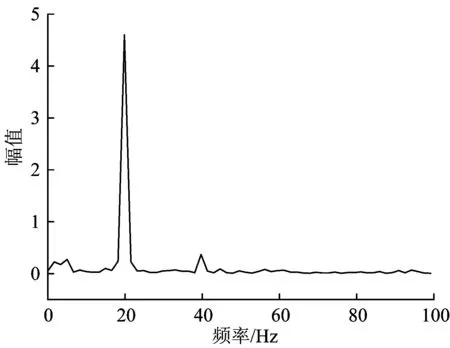
图10 原始加速度信号的频谱分析图
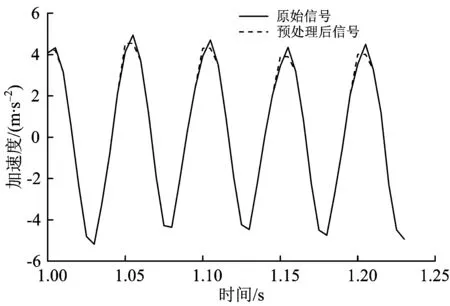
图11 预处理后的振动轮加速度信号
4.2.2压实指标相关性校检
选取现场采集的9段加速度信号进行预处理,并根据上述加速度信号谐波平衡法理论推导结果,求得压实过程中每个CMV对应的土体参数ks和cs。为验证所得土体参数ks和cs的可靠性,在此基础上,进一步进行压实传统指标Evd的检测试验,并利用所测Evd分别与对应的CMV、土体参数ks和cs进行相关性校检,每段信号对应的校检结果见表6。

表6 各段信号对应的Evd与各指标相关系数的校检结果
由表6可看出,各段信号的CMV与Evd、刚度ks与Evd的相关性系数均超过了0.7,均满足现行TB 10108—2011《铁路路基填筑工程连续压实控制技术规程》的要求。而对于阻尼cs,信号2中阻尼cs与Evd的相关系数小于0.7,且其相关系数较其余2个指标均较小,不宜作为压实质量评价指标,故只需比较ks与CMV的适用性。分析ks与CMV的相关系数可知,除了信号4中刚度ks的相关系数小于CMV的相关性系数外,其余ks的相关系数均大于CMV对应的相关性系数,且信号4中ks与CMV两者的相关系数非常接近,可近似认为相等。由此可初步判断,ks与Evd的相关性优于CMV。另外,CMV是基于动力响应信号的频谱分析,通过计算加速度1阶谐波与基频的振动比表征压实质量,是一个通过试验确定的指标。而Evd与ks均基于弹性均质半无限体空间理论,通过对碾压面所受动力信号进行分析,表征碾压面在动荷载作用下的特性,具有充足的理论基础,且Evd作为压实质量的传统检测指标已广泛应用。综上,可知土体刚度指标ks具有相应的理论基础,且试验结果亦满足相关规范要求,能够表征土体的压实状态,故提出将识别的土体刚度作为铁路路基连续压实的新参考指标。
5 结 论
(1)在分析现有压实质量连续检测指标存在不足的基础上,引入谐波平衡识别法,利用多维最小二乘法,推导出压实土体参数识别方程,编制了相应识别程序进行仿真试验。
(2)仿真试验表明:识别程序识别的误差随着谐波数的增加而递减;在噪声功率为0.010,0.025和0.050的情况下,土体参数的识别误差均小于5%,且真实和识别的机架、振动轮加速度信号的相似度都非常接近1,验证了谐波平衡法具有较强的抗干扰性;利用谐波平衡法识别的土体参数具有很高的可靠度,可准确反映土体的压实程度。
(3)通过现场压实试验,求解并对比了CMV、阻尼cs和刚度ks与Evd的相关性,证明阻尼cs不宜作为土体压实的评价指标,并从理论、试验两方面证明了土体刚度ks作为铁路路基土体压实指标的可行性。
[1]VENNAPUSA P K R, WHITE D J, Morris M D. Geostatistical Analysis for Spatially Referenced Roller-Integrated Compaction Measurements[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 136(6): 813-822.
[2]FACAS N W, RINEHART R V, MOONEY M A. Development and Evaluation of Relative Compaction Specifications Using Roller-Based Measurements[J]. Geotechnical Testing Journal, 2011, 34(6): 129-135.
[3]THURNER H, SANDSTROM A. Continuous Compaction Control, CCC[C]//European Workshop Compaction of Soils and Granular Materials, Presses Ponts et Chaussées. Paris: Presses Ponts et Chaussees, 2000: 237-246.
[4]PUPPALA A J. Estimating Stiffness of Subgrade and Unbound Materials for Pavement Design[M]. Washington,D.C.:Transportation Research Board, 2008.
[5]MOONEY M A, ADAM D. Vibratory Roller Integrated Measurement of Earthwork Compaction: An Overview[C]//Proceedings of the 7th International Symposium on Field Measurements in Geomechanics (FMGM’ 07). Boston:American Society of Civil Engineers,2007:1-12.
[6]MOONEY M A. Intelligent Soil Compaction Systems[M]. Washington,D.C.:Transportation Research Board, 2010.
[7]ANDEREGG R, KAUFMANN K. Intelligent Compaction with Vibratory Rollers: Feedback Control Systems in Automatic Compaction and Compaction Control[J]. Journal of the Transportation Research Board, 2004, 1868(1): 124-134.
[8]MOONEY M A, GORMAN P B, GONZALEZ J N. Vibration-Based Health Monitoring of Earth Structures[J]. Structural Health Monitoring, 2005, 4(2): 137-152.
[9]徐光辉. 路基系统形成过程动态监控技术[D].成都:西南交通大学,2006 :5-8.
(XU Guanghui.Technique of Dynamic Monitor on Forming Process of Subgrade System[D].Chengdu:Southwest Jiaotong University,2006:5-8.in Chinese)
[10]KERSCHEN G, WORDEN K, VAKAKIS A F, et al. Past, Present and Future of Nonlinear System Identification in Structural Dynamics[J]. Mechanical Systems and Signal Processing, 2006, 20(3): 505-592.
[11]VAN Susante P J, MOONEY M A. Capturing Nonlinear Vibratory Roller Compactor Behavior through Lumped Parameter Modeling[J]. Journal of Engineering Mechanics, 2008, 134(8): 684-693.
[12]BAIDYA D K, MURALIKRISHNA G, PRADHAN P K. Investigation of Foundation Vibrations Resting on a Layered Soil System[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(1): 116-123.
[13]张青哲.土基振动压实系统模型与参数研究[D].西安:长安大学,2010:46-49.
(ZHANG Qingzhe. Technique of Dynamic Monitor on Forming Process of Subgrade System[D].Xi’an:Chang’an University,2010:46-49.in Chinese)
[14]窦苏广,叶敏.基于谐波平衡的参激系统非线性参数识别频域法[J].振动与冲击,2009,28(12):123-127.
(DOU Suguang,YE Min. Nonlinear Identification in Frequency Domain for Parametric Excitation System Based on Harmonic Balance Principle[J].Journal of Vibration and Shock,2009,28(12):123-127.in Chinese)
[15]SIMINIATI D, HREN D. Simulation on Vibratory Roller-Soil Interaction[J]. Advanced Engineering, 2008, 2(1): 111-120.
[16]付莹.非线性参数激励系统的参数识别方法研究[D].杭州:浙江大学,2008.
(FU Ying.Studies on Parameter Identification of Nonlinear Parameter-Excited Vibration System[D].Hangzhou:Zhejiang University,2008.in Chinese)
[17]杨炜辰,凌海风,武鹏,等.一种基于相似度矩阵的本体检索匹配算法[J].计算机工程与应用,2013,49(22):127-131.
(YANG Weichen, LING Haifeng, WU Peng, et al. Ontology Retrieve Matching Algorithm Based on Similarity Matrix Body[J].Computer Engineering and Applications, 2013, 49(22):127-131.in Chinese)
[18]聂志红,焦倓,王翔.基于地统计学方法的铁路路基压实均匀性评价[J].中国铁道科学,2014,35(5):1-6.
(NIE Zhihong, JIAO Tan, WANG Xiang. Compaction Uniformity Evaluation of Railway Subgrade Based on Geostatistics[J]. China Railway Science, 2014, 35(5): 1-6.in Chinese)
[19]易飞.振动压路机振动加速度实时检测及数据处理研究[D].重庆:重庆交通大学,2011:16-40.
(YI Fei. Vibratory Roller Vibration Acceleration Synchronous Detection and Data Processing[D]. Chongqing: Chongqing Jiaotong University, 2011:16-40.in Chinese)
