地铁大线网条件下乘客SPSL路径选择模型

张永生，姚恩建，刘莎莎，李斌斌

(北京交通大学 交通运输学院，北京　100044)

我国的城市地铁网络发展迅猛，北京、上海、广州等特大城市已经形成了地铁大线网，使得地铁乘客出行可以选择的路径更多，但影响路径选择的因素也更加多样化。对地铁乘客路径选择行为进行分析，深入挖掘影响地铁乘客路径选择的因素和各影响因素之间的相关关系，并测算出地铁乘客综合考虑各因素后选择不同路径的比例，是为地铁乘客提供个性化路径导航服务的基础，也是生成断面流量、换乘量和线路流量等地铁客流量的前提，而地铁客流量可以为地铁运营管理部门确定票务清分比例、制定地铁列车开行计划、策划地铁客流组织、规划地铁新线开通方案、研究地铁新线开通对既有地铁线网的影响和评估地铁服务水平等提供数据支持[1]。因此，开展地铁乘客路径选择行为的研究具有重要的理论和现实意义。

离散选择模型[2]从微观经济学角度将乘客个体的路径选择过程模型化，可以很好地揭示影响乘客个体路径选择的因素及各因素间的相互替代关系，是研究地铁乘客路径选择行为的主要工具之一。离散选择模型用乘客对路径的感知效用表示乘客感知到的各因素对路径选择的综合影响，路径选择过程就是选择乘客感知效用最大路径的过程。在众多的离散选择模型中，MNL (Multinomial Logit)模型[3]由于具有易于估算参数和拓展应用等优点，而被国内外学者广泛应用。Daamen[4]、Raveau[5]分别基于MNL模型构建了轨道交通乘客路径选择模型，探讨了轨道交通服务水平、个体属性、出行目的、路网拓扑结构等因素对乘客路径选择偏好的影响；国内学者四兵锋[6]、张永生[7]以及刘莎莎[8]等分别基于该模型研究了轨道交通网络均衡、客流需求预测以及个性化路径导航等问题。但MNL模型假设其误差项服从IID (Independent and Identical Distribution) Gumbel分布，从而导致了路径重复问题和忽视了OD(Origin-Destination)对尺度效应(即长短路)问题。路径重复问题指的是MNL模型因假设路径之间独立不相关，而忽略了不同路径之间因共享部分路段而产生的相互影响关系；OD对尺度效应问题指的是MNL模型因假设乘客在不同OD对下的路径选择行为是一致的，而忽视了OD对之间的差异性。针对MNL模型存在的路径重复问题，一些学者对MNL模型进行了改进，比如Raveau[9]基于MNL模型构建的C-Logit模型，可用于分析地铁乘客路径选择中出现的路径重复问题，但缺少对OD对尺度效应问题的讨论。刘剑锋[10]、Chen[11]和赖信君[12]等针对OD对尺度效应问题进行了研究，但他们的研究在应用于多因素影响下的乘客路径选择问题时存在参数标定困难，而且只考虑了乘客对路径的感知效用的感知误差随OD对尺度效应的变化而变化的问题，忽视了地铁某些因素(如换乘次数)对路径效用的影响随乘车时间的增加而增加的现象。

综上，本文根据地铁路网的特点，综合考虑路径重复问题和OD对尺度效应问题，采用构建PSL(Path Sized Logit)模型[13]的思路描述路径重复问题，进而构建地铁乘客SPSL(Scaled Path Sized Logit)路径选择模型，分析OD对尺度效应影响下地铁乘客路径选择各影响因素间的相互替代关系，并将其应用到换乘量估算中。

1　路径选择建模

1.1　地铁网络中的OD对尺度效应

为更直观地分析地铁网络中的OD对尺度效应，本文只考虑旅行时间和换乘次数对路径效用的影响。如图1所示，在2个OD对R1—S1和R2—S2中，R1和R2为出发站，S1和S2为目的站，A和B为换乘站，L1，L2，L3和L4分别是这2个OD对的路径，且对应的旅行时间分别为110，100，20和10 min，各路径独立且不相关。旅行时间包含乘客从进出发站到出目的站花费的包括乘车时间和换乘时间在内的所有时间，且假设乘车时间、换乘时间等各种时间对乘客路径选择的影响是相同的。

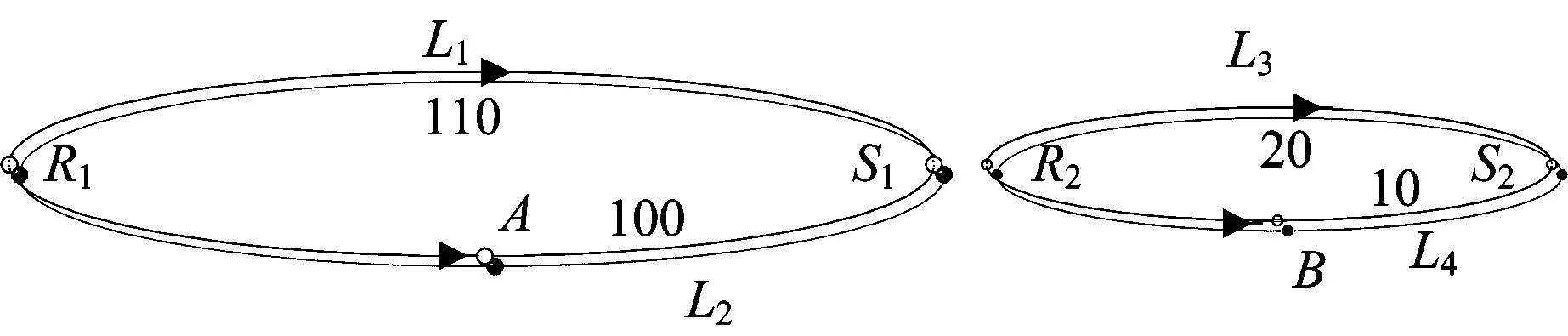
图1　地铁网络OD对尺度效应示意图

根据MNL模型，各路径被选择的概率为P(L1)=P(L3)和P(L2)=P(L4)，显然，该结果并不符合实际。为说明OD尺度效应对路径选择结果的影响，本文进行如下分析。

(1)如果当车站A和B不是换乘站而是通过站时，由于乘客在实际出行中对经由各条路径所花费的出行时间均存在感知误差，即相对于20和10 min的短路径，乘客仅靠直觉无法准确区分走100与110 min长路径时的真实差距。因此，按每个OD对下各条路径的选择概率之和为100%考虑，则OD对R1—S1的路径L1和L2的选择概率应该相差不大，更接近50%。比如若P(L1)=40%， 则P(L2)=60%； 而OD对R2—S2的路径L3和L4的选择概率则会有明显的差异， 比如P(L3)<40%， 则P(L4)>60%。 由此可以得出各条路径实际被乘客选择的概率会满足P(L4)>P(L2)>P(L1)>P(L3)，这说明OD对之间的差异性会影响路径的选择概率。虽然这2组数据的差值均为10 min，但该差值在OD对R1—S1下对路径选择的影响要小于在OD对R2—S2下，即随着OD对间最短旅行时间的增加，乘客对路径的感知效用的感知误差也随之增大，这就是现有文献中常提到的OD对尺度效应。

(2)如果当车站A和B是换乘站时，那么对于乘客来说，不只是增加了换乘时间，还有体力和精神上的付出，因此换乘次数和旅行时间都会影响路径选择的结果。但因换乘次数和旅行时间是不同量纲的变量，所以无法直接对比两者对路径选择结果的影响。根据随机效用理论，通过边际替代率转换，可以得到换乘次数和旅行时间之间的相互替代关系，即换乘1次相当于增加多长旅行时间的替代关系。如果按照传统Logit路径选择模型和为解决OD对尺度效应的既有改进Logit模型[10-12]，对该替代关系的变量取定值，即不会随着OD对间最短旅行时间的变化而变化。但是，本文为直观地说明该变量的取值具有变化性，现考虑换乘次数与旅行时间的替代关系，假设在OD对R2—S2下换乘1次相当于又额外增加了10 min的旅行时间；由图1虽然路径L4的旅行时间比路径L3的少10 min，但由于乘客走路径L4时比走路径L3多了1次换乘，因此考虑换乘次数与旅行时间的替代关系后乘客走路径L4花费的旅行时间也相当于20 min，此时路径的选择概率满足P(L4)=P(L3)。若OD对间最短旅行时间增大到OD对R1—S1的规模，则根据实际经验和现有文献对OD对尺度效应的描述，相对于20和10 min的路径，乘客更难准确区分100和110 min路径的真实差距，即虽然2组数据的差值均为10 min，但该差值在OD对R1—S1下对路径选择的影响要小于在OD对R2—S2下的；因此，从走路径L2比L1多了1次换乘考虑，并结合对路径L3和L4的选择概率，此时乘客对路径L1和L2的选择概率应满足P(L1)>P(L2)。该结果说明在OD对R1—S1下换乘1次对乘客对路径的感知效用的影响要大于考虑换乘次数与旅行时间的替代关系后所增加的10 min旅行时间对路径效用的影响，即在OD对R1—S1下换乘1次等价的旅行时间大于10 min。上述现象表明，随着OD对间最短旅行时间的增加，换乘次数对路径效用的影响越来越大，这就是现有文献所忽视的另一种OD对尺度效应。

为反映OD对尺度效应的上述2种表现，同时考虑路径重复问题，本文构建了地铁乘客SPSL路径选择模型，并对其进行应用检验和分析。

1.2　地铁乘客SPSL路径选择模型

影响地铁乘客路径选择行为的因素有很多，主要有乘车时间(包括进站时间、列车行驶时间和列车站停时间等)、换乘次数及换乘时间(包括换乘走行时间和换乘候车时间等)、舒适程度等。其中，路径的长度因与旅行时间(乘车时间与换乘时间之和)具有很大的相关性而不被本文考虑。为综合考虑各因素对地铁乘客路径选择行为的影响，通常利用随机效用理论将各影响因素统一为乘客对路径的感知效用，即乘客n对从车站r到s的路径k的感知效用可以表示为

(1)

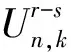
(2)

根据Gumbel分布的性质[2]，乘客n选择路径k的概率为

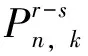
(3)

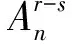
(4)

(5)

在MNL模型中，一般将不同OD对下的尺度系数取为相同值，即乘客对不同OD对下各条路径的路径效用的感知误差是一样的，忽略了OD对之间的差异性。这就是导致OD对尺度效应问题的原因之所在。实际情况是，在不同的OD对下，乘客对路径效用的感知误差应该是不一样的。乘客对路径效用的感知误差不仅受感知效用函数中各因素的影响，还受一些不可观测因素(如对路径的熟悉程度等)的影响，因此，在理论上是无法获得感知误差精确取值的，也即式(2)中的尺度系数无法准确确定。但地铁网络中不同OD对尺度系数之间的差异(即感知误差的方差的差异)在一定程度上因为主要受最短乘车时间变化的影响，所以，某OD对的尺度系数可以近似表示为该OD对间最短乘车时间的函数，描述如下。

(6)

式中，考虑到参数μ′和感知效用函数确定项中的参数在标定时的可识别性，参数μ′一般取为1。

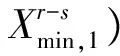
(7)

其中，

(8)

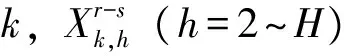
最后，将上述各式联立即构成地铁乘客SPSL路径选择模型，即乘客n选择路径k的概率为

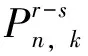
(9)

另外，如果假定乘客是同质的，则模型参数θn,1,θn,2,…,θn,H可以等价为参数θ1，…，θH，这些参数可以利用极大似然估计算法以及现有的成熟软件如Gauss，NLogit等很容易进行估计，具体过程限于篇幅不再赘述。

1.3　影响因素间的替代关系分析

(10)

2　应用分析

如图2所示，截止2014年7月份，不含自动运输系统(APM线)，广州地铁共有运营线路8条，车站136座(其中换乘站19座)，运营里程达250 km以上。广州地铁网络比较复杂，乘客出行的可选路径较多，适合用文本地铁乘客路径选择模型进行分析。

图2　广州地铁线网示意图

2014年7月份对广州地铁乘客出行特征进行调查，共收回有效问卷14 142份。通过对调查数据的分析，获得了乘客真实的出行路径和乘客的出行特性(如进站时间段等)。

构造备选路径集合时，对于式(4)和式(5)，本文取d=3，b=30 min，c=2。基于调查数据中的RP(Revealed Preference)数据(即乘客真实的出行路径)，利用极大似然估计法对式(9)中的参数进行估计。考虑到高峰时段出行的乘客大都以通勤出行为主，与平峰时段出行的乘客成分相比差别很大，因此分别按高峰时段(7：00—9：00和17：00—19：00)和平峰时段2种情况对地铁乘客出行路径选择模型的参数进行估计，结果见表1。

由表1可知，各参数t-值的绝对值均大于1.96，表明有95%的可信度认为各参数的估计值可信，可以用于各参数的标定。此外，乘车时间、换乘次数和换乘时间的系数均为负值，表明随着路径乘车时间、换乘次数和换乘时间的增加，乘客选择该路径的概率越小，即乘客倾向于选择乘车时间短、换乘次数少和换乘时间短的路径；舒适程度的系数θ4为正值，表明在相同的情况下，乘客更愿意选择满载率比较较小的路径。两模型的拟合优度ρ2均大于0.2，说明模型可以很好地解释数据的变化规律，模型的整体拟合效果比较理想。对比两模型的拟合优度，不论是在高峰时段出行还是平峰时段出行，SPSL模型的均大于MNL模型的，说明SPSL模型对调查数据的解释性优于MNL模型。

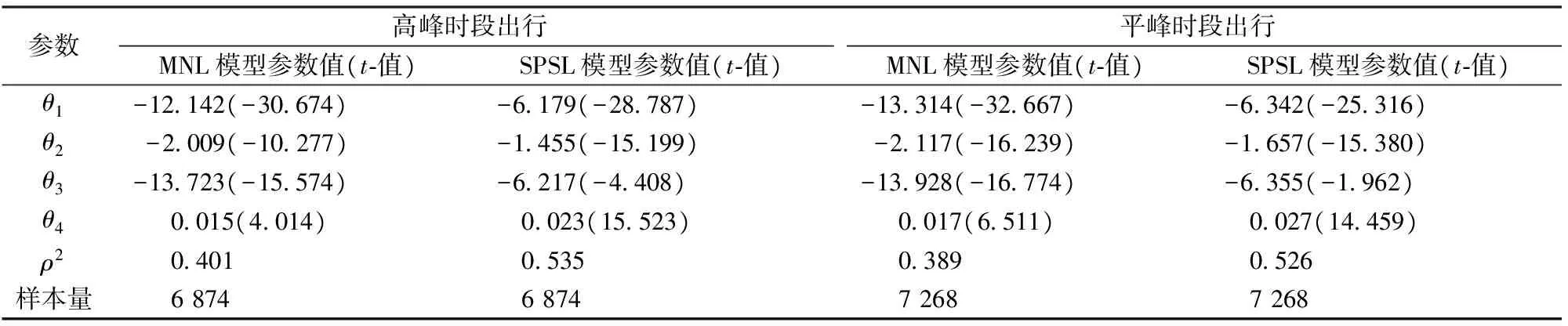
表1　模型各参数的估计值

根据对SPSL模型各参数的标定结果，利用公式(10)即可得到每个OD对下广州地铁乘客在高峰时段和平峰时段出行时的单位换乘次数等效乘车时间。通过统计，以OD对间最短乘车时间为横轴，以OD对的数量为纵轴，得到OD对数量分布情况，如图3所示。

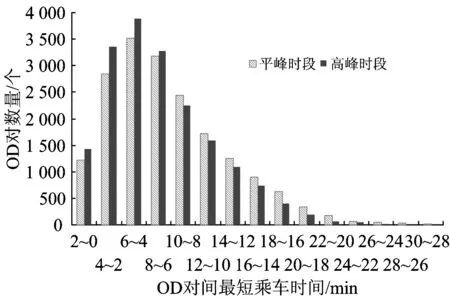
图3　OD对数量分布

由图3可知，单位换乘次数等效乘车时间在不同OD对下的取值不同，印证了前文关于换乘次数对路径效用的影响随着OD对路径上最短旅行时间的变化而变化的分析。乘客在高峰和平峰时段出行对应的单位换乘次数等效乘车时间的平均值分别为7.105和7.883 min·次-1，高峰时段出行时的单位换乘次数等效乘车时间小于平峰时的，说明相对于平峰时段，乘客在高峰时段出行时换乘次数对路径效用的影响较小，乘客更加偏好旅行时间短的路径；同时，也说明乘客在平峰时段出行时对换乘次数更加敏感，更喜欢选择换乘次数少的路径。

换乘量是换乘通道客流组织、各条线路协同运行计划制定、换乘效率评估和换乘站设计等的依据，也是微观的个体路径选择概率在宏观的客流数据中的体现。本文通过估算换乘量，一方面可以说明路径选择模型的应用场景，另一方面也可以间接验证路径选择模型参数的标定结果。

换乘量的估算方法是：分别基于高峰和平峰时段的路径选择模型以及式(9)，可以获得乘客在高峰和平峰时段从路径集合中选择各条路径的概率，然后乘以不同时间窗下的OD客流量即可获得在该时间窗下选择各条路径出行的客流量，进而基于列车时刻表便可统计得到各换乘站在各时间窗下的换乘量，最终将各时间窗下的换乘量累加即可得到全天换乘量。

本文选用广州地铁2014年8月份的平均OD客流量、路网拓扑数据、运营基础数据等作为输入数据，获得路径选择模型中对应不同路径的各个变量值和每15 min时间窗下的OD客流量，并以广州地铁目前所用清分算法得到的换乘量为验证数据。考虑到广州地铁统计的每15 min时间窗下的OD客流量数据是以乘客出站时刻所处的时间窗为判断依据的，因此基于路径流量进行客流统计时需从路径的终点站倒推至路径的起始站。最终，得到了各换乘站在各换乘方向上全天的换乘量，共138组数据，其中，全天换乘量以45度线图形式列于在图4中，该图中的横轴为验证值，纵轴为估算值，数据点越接近45度线，表明估算值越接近验证值；图4(a)用于验证MNL模型，图4(b)用于验证SPSL模型。对比图4(a)和图4(b)可知，图4(b)中的数据点相对更集中于45度线附近，表明基于SPSL模型得到的各换乘站在各换乘方向上全天换乘量估算值更接近于验证值，而且基于MNL模型的估算值的平均相对误差为9.34%，基于SPSL模型的估算值的平均相对误差为6.98%，由此结果表明SPSL模型优于MNL模型。另外，基于SPSL模型估算的换乘量精度也能满足运营管理部门对数据精度的需求，而且，随着乘客出行个性化需求的增加和运营管理部门对数据精准化需求的提高，该模型有很好的应用前景。

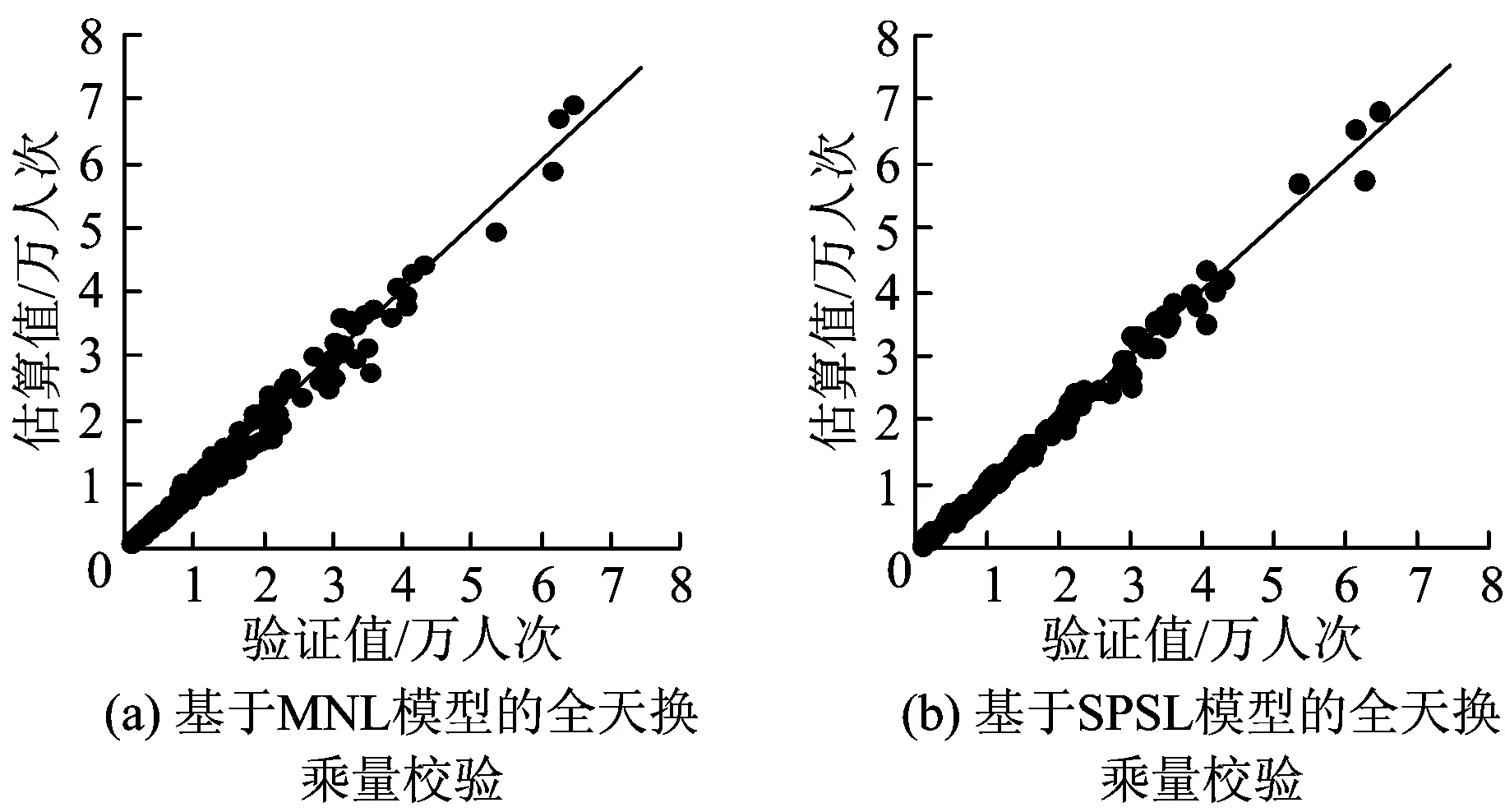
图4　换乘量估算效果验证

3　结　论

在地铁大线网条件下乘客的路径选择规律更加复杂，OD对尺度效应对乘客路径选择结果的影响更加明显。现有的地铁乘客路径选择建模普遍对OD对尺度效应考虑不足，针对OD对尺度效应带来的乘客对路径效用感知误差随OD对尺度的增大而增大和换乘次数等对路径效用的影响随着乘车时间的增加而增大等问题，同时考虑重复路径问题，本文构建了地铁乘客SPSL路径选择模型。通过利用广州地铁调查数据对该模型的参数进行标定和基于标定的模型对换乘量进行估算，证实了本文所建SPSL模型优于MNL模型，说明本文所建模型可以很好地反映OD对尺度效应对乘客路径选择偏好的影响。同时，文中分析了不同出行时间段下乘客的路径选择偏好，发现高峰时段出行时单位换乘次数等效乘车时间的平均值小于平峰时段出行，说明相对于高峰时段，乘客在平峰时段出行时更加不喜欢换乘次数多的路径；相对于平峰时段出行，乘客在高峰时段出行时更愿意选择旅行时间短的路径。

[1]吴小萍, 陈秀方. 城市轨道交通网络规划理论方法研究进展 [J]. 中国铁道科学, 2003, 24(6): 111-117.

(WU Xiaoping, CHEN Xiufang. Progress of Study on Urban Mass Transit Network Planning Theory and Methodology [J]. China Railway Science, 2003, 24(6): 111-117. in Chinese)

[2]BEN-AKIVA M, LERMAN S R. Discrete Choice Analysis: Theory and Application to Travel Demand [M]. 7th ed. London: MIT Press, 1985.

[3]MCFADDEN D. The Revealed Preferences of Government Bureaucracy[J]. Bell Journal of Economics Management Science, 1968(6): 401-416.

[4]DAAMEN W, BOVY P H L, HOOGENDOORN S P, et al. Passenger Route Choice Concerning Level Changes in Railway Stations[C]//The 84th Transportation Research Board Annual Meeting. Washington D C, US：2005.

[5]RAVEAU S, MUNOZ J C, GRANGE L D. A Topological Route Choice Model for Metro[J]. Transportation Research Part A: Policy and Practice, 2011, 45(2): 138-147.

[6]四兵锋, 毛保华, 刘智丽. 无缝换乘条件下城市轨道交通网络客流分配模型及算法[J]. 铁道学报, 2007, 29(6): 12-18.

(SI Bingfeng, MAO Baohua, LIU Zhili. Passenger Flow Assignment Model for Urban Railway Traffic Network under the Condition of Seamless Exchange[J]. Journal of the China Railway Society, 2007, 29(6): 12-18. in Chinese)

[7]张永生, 姚恩建, 代洪娜. 成网条件下地铁换乘量预测方法研究[J]. 铁道学报, 2013, 23(11): 1-6.

(ZHANG Yongsheng, YAO Enjian, DAI Hongna. Transfer Volume Forecasting Method for the Metro in Networking Conditions[J]. Journal of the China Railway Society, 2013, 23(11): 1-6. in Chinese)

[8]刘莎莎, 姚恩建, 张永生. 轨道交通乘客个性化出行路径规划算法[J]. 交通运输系统工程与信息, 2014, 14(5): 100-104.

(LIU Shasha, YAO Enjian, ZHANG Yongsheng. Personalized Route Planning Algorithm for Urban Rail Transit Passengers[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(5): 100-104. in Chinese)

[9]RAVEAU S, GUO Z, MUNOZ J C, et al. A Behavioural Comparison of Route Choice on Metro Networks: Time, Transfers, Crowding, Topology and Socio-Demographics[J]. Transportation Research Part A: Policy and Practice, 2014, 66: 185-195.

[10]刘剑锋, 孙福亮, 柏赟, 等. 城市轨道交通乘客路径选择模型及算法[J]. 交通运输系统工程与信息, 2009, 9(2): 85-90.

(LIU Jianfeng, SUN Fuliang, BAI Yun, et al. Passenger Flow Route Assignment Model and Algorithm for Urban Rail Transit Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(2): 85-90. in Chinese)

[11]CHEN A, PRAVINVONGVUTH S, XU X D, et al. Examining the Scaling Effect and Overlapping Problem in Logit-Based Stochastic User Equilibrium Models[J]. Transportation Research Part A: Policy and Practice, 2012, 46(8): 1343-1358.

[12]赖信君, 余志, 李军. 相对阻抗Logit路径选择模型的推导、应用及验证[J]. 交通运输系统工程与信息, 2012, 12(2): 85-90.

(LAI Xinjun, YU Zhi, LI Jun. Derivation, Implementation and Examination of Logit Route Choice Model with Relative Impedance[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(2): 85-90. in Chinese)

[13]BEN-AKIVA M, BIERLAIRE M. Discrete Choice Methods and Their Applications to Short Term Travel Decisions[M]. US：Springer, 1999.