基于桥梁施工节段长度的车—线—桥耦合系统轨道不平顺敏感波长分析
2016-04-10杨宏印卢海林陈旭勇
杨宏印,卢海林,陈旭勇,王 波
(1.武汉工程大学 资源与土木工程学院,湖北 武汉 430073;2.中铁大桥科学研究院有限公司,湖北 武汉 430034)
车—线—桥耦合振动是高速铁路研究中的一个关键问题。在为研究该问题而进行有限元建模时,由于往往采用相同长度的桥梁单元和轨道单元[1-3],使得桥跨结构越大,建模和计算越复杂。为提高计算效率,文献[4—5]指出可以根据实际情况采用不同长度的单元进行划分。变截面连续梁桥具有受力性能优越和跨越能力强等优点,已被广泛用于铁路交通中。这种桥型通常采用分节段施工法,为模拟施工过程及分析长期受力性能,建模时需要考虑实际施工节段。此外,轨道不平顺是引起轮轨动力作用变化,进而诱发整个车—线—桥系统振动的重要激励[6-8]。轨道随机不平顺通常采用连续波长描述,而明确轨道不平顺的敏感波长是线路运营亟待解决的问题[9-10]。
本文针对车—桥耦合振动计算量大的问题,提出用任意长度组合的轨道—桥梁耦合单元建立基于桥梁施工节段长度的车—线—桥耦合系统有限元模型的方法,用于车—线—桥耦合系统振动分析;并结合任意波长不平顺的生成方法研究轨道随机不平顺的敏感波长。
1 基于桥梁施工节段长度的系统耦合振动模型
图1为列车通过某高速铁路变截面连续梁桥时的耦合系统模型。它包含列车、轨道和桥梁共3个子系统,其间通过轮轨关系和桥轨关系连接起来。1个车辆包含1个车体、2个转向架和4个轮对,车体和转向架有沉浮和点头2个自由度,轮对只有沉浮1个自由度,共有10个自由度。通过平面Euler-Bernoulli梁模拟轨道和桥梁,并用线性化的Hertz弹性接触理论模拟轮轨接触[11-12]。桥上铺设双块式无砟轨道,将轨道板等二期恒载以参振质量的方式加于桥梁模型中,而将钢轨视为离散弹性点支承上的梁[6]。
为提高车—线—桥耦合振动的计算效率,采用较短的轨道单元。将桥梁和轨道结构离散,并根据要求细化轨道单元,得到图2所示不同长度组合的轨道—桥梁耦合单元,图中l为单元长度,下标b和r分别代表桥梁和轨道,且lb=Alr,A为1个桥梁单元上存在的轨道单元个数,kr和cr分别为轨下胶垫的等效刚度和阻尼。

图1 列车—轨道—桥梁系统模型

图2 任意长度组合的轨道—桥梁耦合单元
桥梁结构采用Rayleigh阻尼,桥梁单元的动力方程为
(1)
其中,

式中:M,C和K分别为质量、阻尼和刚度矩阵;qe为位移向量;上标e表示单元;m为轨道单元编号;N为Hermite插值向量;Fmrb(x,t)为轨道传给桥梁的力。
轨道传给桥梁的力Fmrb可表示为
(2)
式中:ymr和yb分别为第m个轨道单元节点处轨道和桥梁的位移,后者可通过桥梁单元节点位移的插值得到。
将式(2)代入式(1),整理可得

(3)
其中,
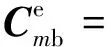
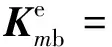
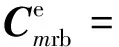
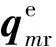
式(3)为图2中单个轨道单元作用下桥梁单元的动力方程。同理可得图2中第m个轨道单元的动力方程为
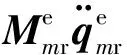
(4)
其中,
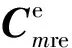
由式(3)和式(4)便可得到图2中第m个轨道—桥梁耦合单元动力方程为
(5)
车辆考虑为刚体[5, 13],第i辆车的动力方程为
(6)
式中:下标v表示车辆。
2 车—线—桥耦合系统有限元方程及求解
根据式(5),由形成矩阵的“对号入座”法则便可得到轨道—桥梁系统动力方程,再结合车辆动力方程式(6),便可得到车—线—桥耦合系统的有限元方程为
(7)
式中:F为荷载向量;下标c表示轮轨耦合项,组合下标为相应的耦合项。
式(7)中Kcr,Krv,Kvr,Fcr和Fcv均与轮轨耦合有关,是时变的,而其他项均是非时变的。在求解时先组装非时变部分,作为初始方程,然后在每个时间步根据时间和实际轮轨接触状态叠加时变部分,便可得到系统振动方程,系统振动方程的组装和计算流程见文献[3]。采用Newmark-β方法直接积分求解,不需迭代。
3 基于桥梁施工节段长度的耦合振动分析
现以某高速铁路连续梁桥为工程实例,建立基于桥梁施工阶段长度的车—线—桥耦合系统模型,进行车—线—桥耦合系统振动分析。桥梁主梁为4跨预应力混凝土连续箱梁,全长160 m,采用挂篮悬臂法施工,混凝土弹性模量为34.5 GPa,阻尼比取0.025,桥墩墩高为20 m,如图3(a)所示。根据施工过程可将主梁划分为50个节段。每个墩左右各存在长度为17 m、高度按抛物线变化的变截面段。每个长17 m的变截面段有5个节段,若按0.5 m进行划分,则共有35个关键截面(见图3(b))。采用MIDAS/Civil建立了桥梁有限元模型,如图3(c)所示。列车由5辆车组成,车辆和轨道模型参数参见文献[3-4]。

图3 变截面连续梁桥模型(单位:m)
对分节段施工的桥梁建模时,应尽量根据其节段的长度划分单元,但桥梁节段长度普遍较大,故为提高计算精度和方便建模,主梁单元仍根据节段长度划分,而将轨道单元细化。为说明这样考虑的合理性,对比分析如下3种单元划分工况。
工况1:主梁单元的划分根据节段的长度划分,桥上轨道单元的划分按0.5 m长划分。
工况2:主梁单元和桥上轨道单元的划分均按0.5 m长划分。
工况3:主梁单元和桥上轨道单元的划分均根据节段的长度划分。
在这3种工况中,对于过渡段上轨道单元的长度均采用0.5 m,桥墩单元的划分也一样。列车以100~425 km·h-1速度通过时,不同工况下左中跨跨中桥梁和轨道的最大加速度响应如图4和图5所示。
由图4和图5可见,工况1和工况2下所得结果非常一致,并且由于工况2中对桥梁单元和轨道单元划分得最精细,因此其分析结果是可靠的[5, 12],这相应说明工况1的计算精度也较高;工况3的结果却与工况1和工况2的结果明显不同,这说明桥梁和轨道的振动加速度响应对轨道单元的长度很敏感。
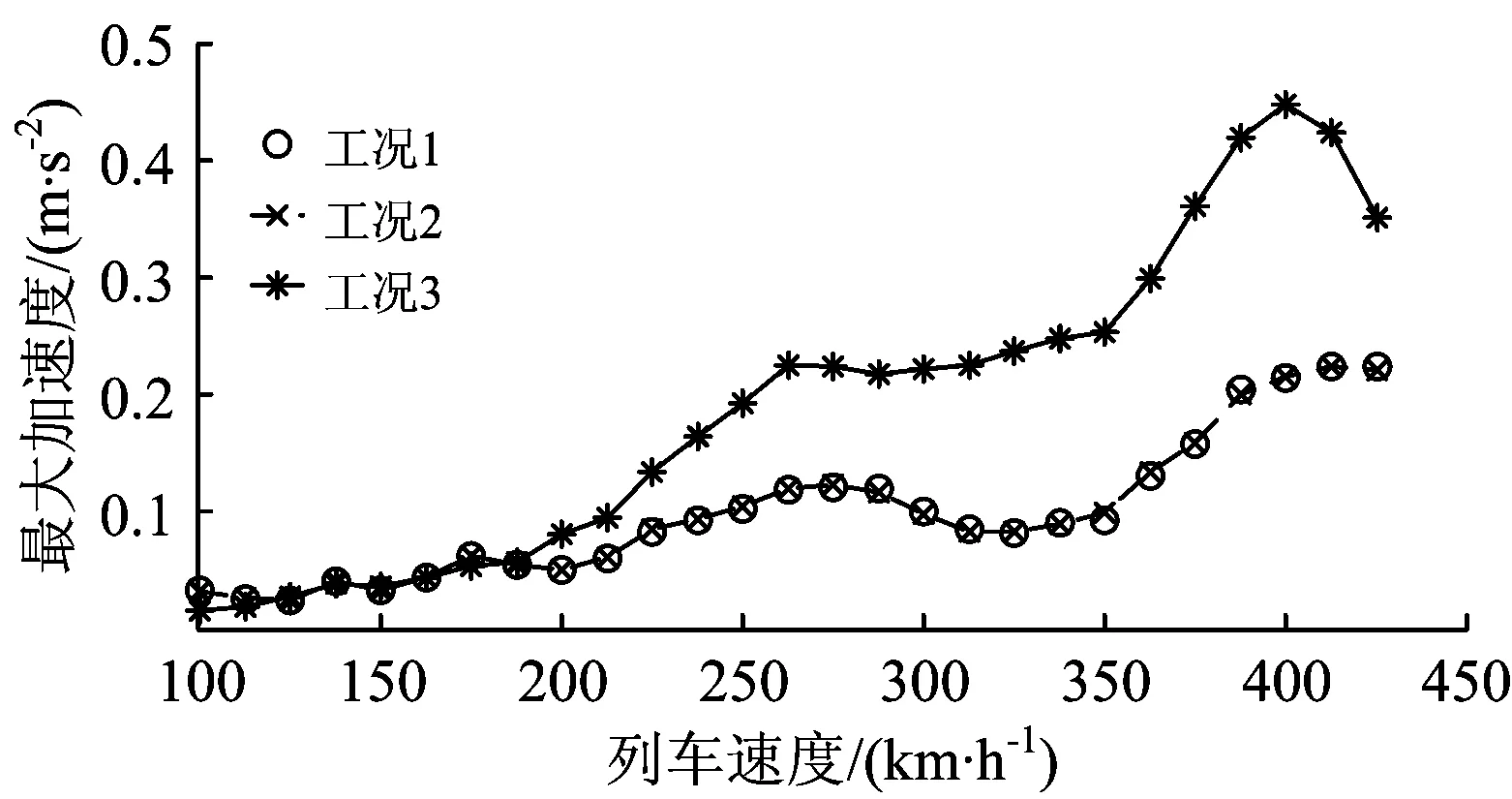
图4 左中跨跨中桥梁最大加速度
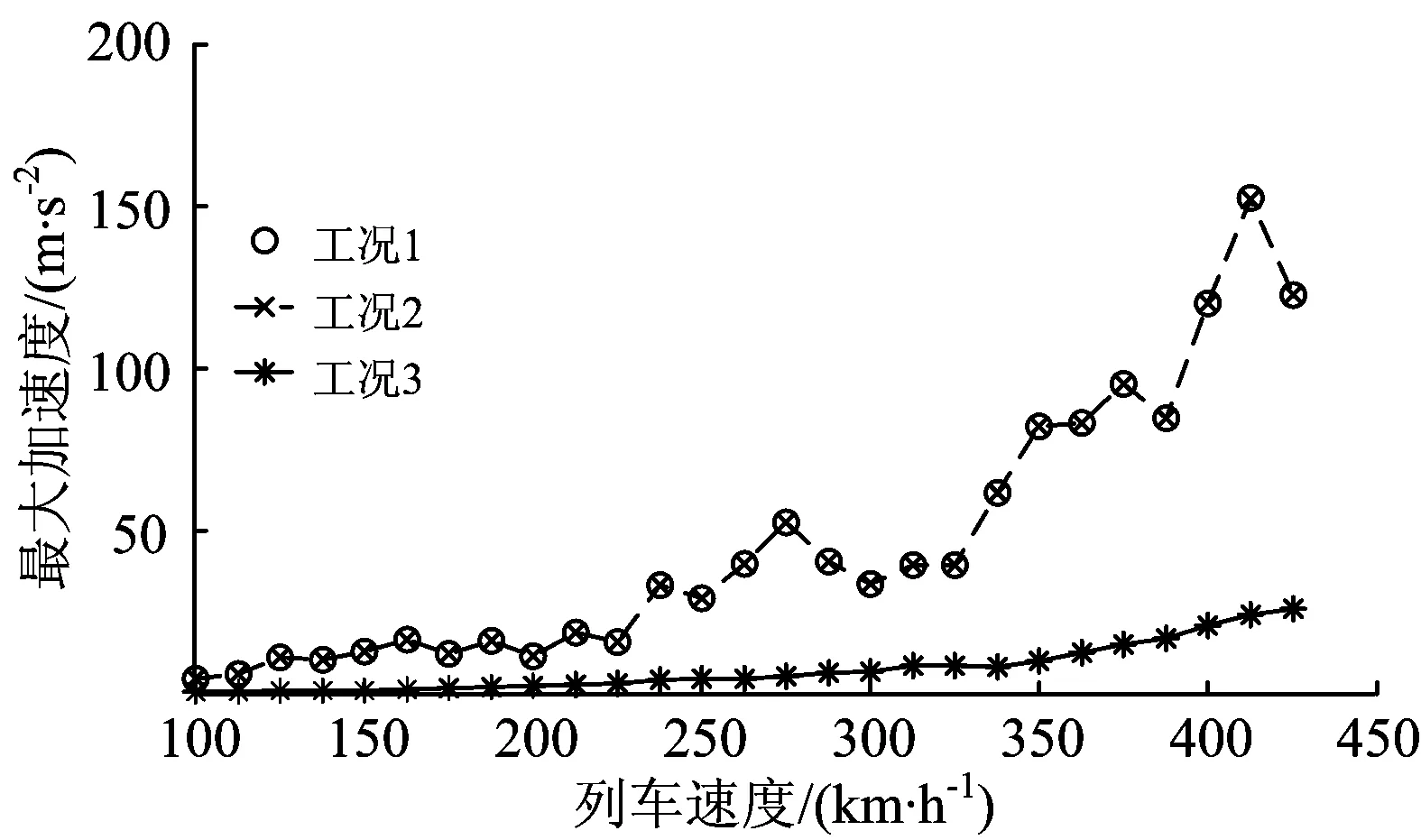
图5 左中跨跨中处轨道最大加速度
图6为列车以200 km·h-1通过时不同工况下中间车辆的1位轮对的轮轨接触力时程曲线。

图6 中间车辆1位轮对的轮轨接触力时程
由图6可见,工况1和工况2下所得结果非常一致,表明桥梁单元的长度取施工节段的长度而只对轨道单元进行细化方法能达到满意的计算精度;但在工况3中,轮轨接触力响应幅值明显比较大,特别在桥墩处的振荡最为剧烈,说明计算结果不可靠。
综上,相对于工况3,在工况1和工况2的单元划分方法均具有较高的计算精度。同工况2相比,在工况1下系统模型的自由度会减少,从而节省计算时间,在相同计算机环境下,两者的计算时间分别为451.7和223.3 s,后者仅为前者的49%。因此,建立耦合系统模型时,应根据实际施工节段长度建立桥梁单元,而采用分布均匀的较短的轨道单元,既能方便建模,也能达到满意的计算精度和计算效率。说明本文方法是可行的。
4 桥上轨道随机不平顺的敏感波长分析
实际线路的几何状态往往是随机的,通常用功率谱密度函数(轨道谱)描述。本文对波长为1~30 m的中波长轨道不平顺采用德国高速铁路“低干扰”谱模拟,即
(8)
式中:Sv(Ω)为功率谱密度;Ω为空间频率,rad·m-1;Av为粗糙度常数,其值为4.032×10-7m2·rad·m-1;Ωc和Ωr为空间截断频率,其值分别取0.824 6和0.020 6 rad·m-1。
对波长为0.03~1 m的短波不平顺,本文采用文献[8]建议的轨道短波不平顺公式模拟,即
Sv(Ω)=0.036Ω-3.15
(9)
根据轨道不平顺频域功率谱密度函数,采用逆傅里叶变换法[6]便可生成轨道不平顺的时域模拟样本。若对整个频率范围进行等带宽离散,再令不在截断频率范围的谱密度为0,便可得到任意波长的时域样本。根据式(8)可生成1~30 m的中波长轨道不平顺的时域样本,根据式(9)可生成0.03~1 m的短波长轨道不平顺的时域样本,将两者叠加便可得到波长为0.03~30 m的轨道不平顺时域样本,如图7所示。
采用上节基于桥梁节段长度的车—线—桥耦合系统有限元模型分析桥上轨道随机不平顺的敏感波长。不同列车速度和轨道不平顺下左中跨桥梁跨中的最大响应如图8所示。

图7 波长区间为0.03~30 m不平顺的时域样本

图8 左中跨跨中桥梁最大响应
由图8可见:各不平顺条件下的桥梁位移响应与轨面光滑时的相差不大,说明轨道不平顺对桥梁位移的影响有限;当列车速度小于175 km·h-1时,桥梁的振动加速度主要来源波长0.03~1 m短波轨道不平顺的贡献;而当列车速度大于175 km·h-1时,波长1~5 m的轨道不平顺对桥梁振动加速度的影响很明显。
图9为不同列车速度和轨道不平顺条件下左中跨跨中桥上轨道最大响应。由图9可见:桥上轨道的最大位移随列车速度变化的趋势不同于桥梁位移,这是由于桥轨间为弹性连接,使得桥梁和轨道的振动不同;当列车速度大于175 km·h-1时,桥上轨道的最大位移受波长1~5 m轨道不平顺的影响较大;桥上轨道振动加速度对波长为0.03~1 m的短波轨道不平顺很敏感。
列车中间车辆的车体最大振动加速度响应如图10所示。由图10可见,列车高速通过时,波长为0.03~1 m的轨道不平顺对车体的振动加速度影响很小,说明车辆的悬挂系统很好地隔离了短波轨道不平顺激起的高频振动;在5~30 m波长中的3个子波长轨道不平顺对车体振动加速度的影响随列车速度的增加而增大。
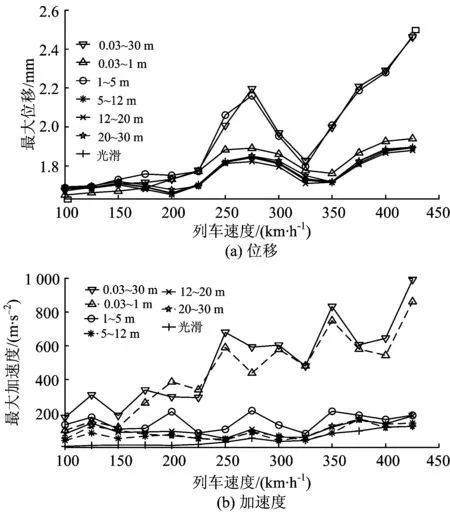
图9 左中跨跨中轨道最大响应

图10 中间车辆的车体最大振动加速度
图11为中间车辆1位轮对的最大轮轨接触力响应。由图11可见,1位轮对的轮轨接触力主要受波长小于5 m的2种波长区间不平顺控制,当列车速度小于175 km·h-1时,受波长为0.03~1 m的短波轨道不平顺影响更大;而当列车速度大于175km·h-1时,1位轮对的轮轨接触力对1~5 m波长的轨道不平顺更为敏感。
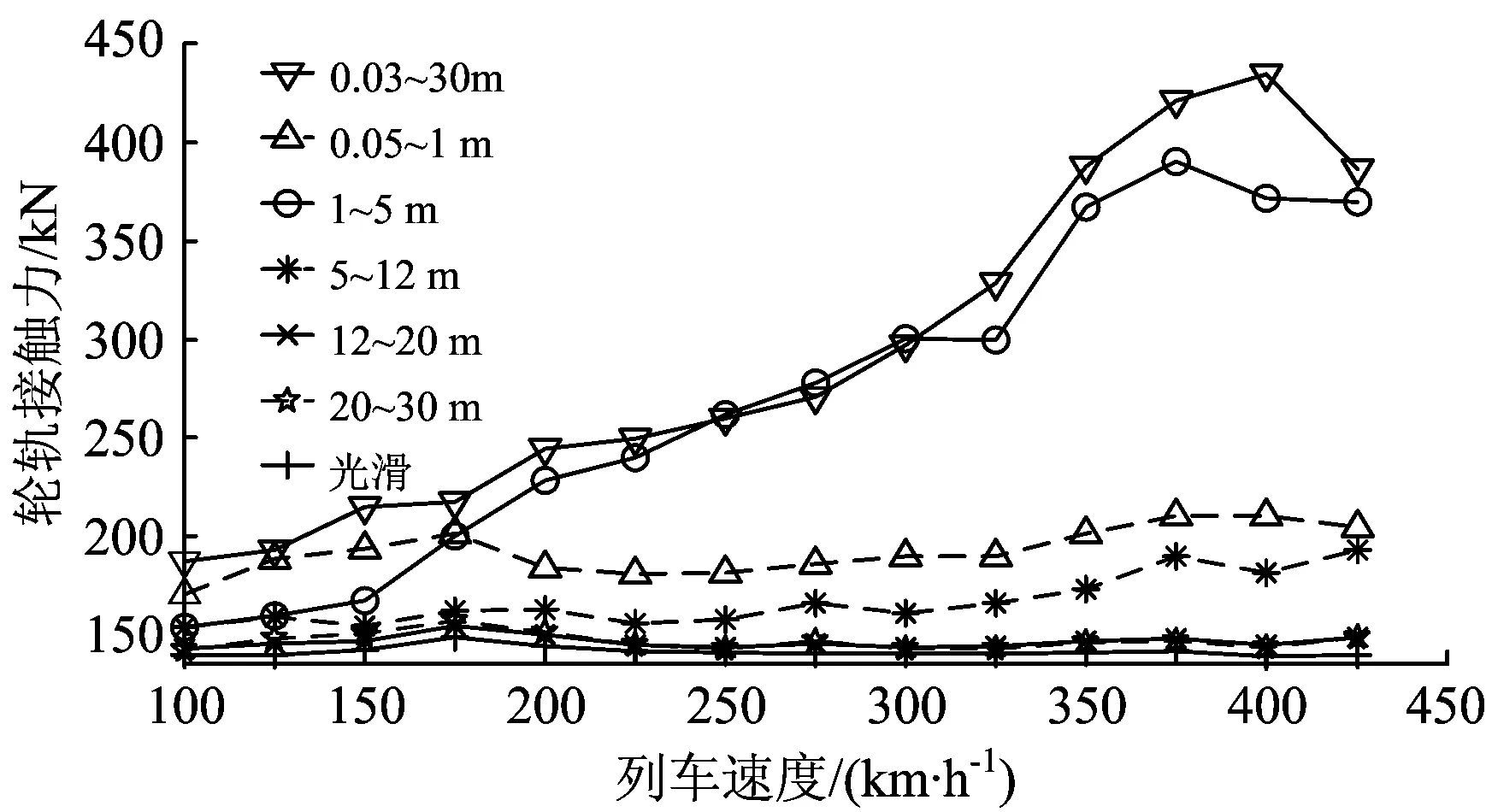
图11 中间车辆的1位轮对最大轮轨接触力
5 结 论
(1) 在车—线—桥耦合振动有限元分析中轨道单元的长度对系统动力响应的影响很大,轨道单元的长度选取不当甚至会导致计算结果不可靠。采用本文提出的基于桥梁施工节段长度的车—线—桥耦合系统有限元模型进行车—线—桥耦合系统的振动分析,能够得到满意的计算精度和计算效率。
(2) 生成的轨道不平顺时域样本的功率谱密度和解析值基本一致,说明对轨道不平顺功率谱密度函数进行逆傅里叶变换生成任意波长轨道随机不平顺的方法是合理、有效的。
(3) 桥梁位移对轨道不平顺不敏感。高速行车时,桥梁振动加速度、轨道位移和列车中间车辆1位轮对轮轨接触力的敏感轨道不平顺波长区间均为1~5 m;波长为0.03~1 m的短波轨道不平顺对轨道振动加速度的影响很大,但对中间车辆车体振动加速度的影响很小,而其他子波长区间不平顺对中间车辆车体振动加速度的影响均较大。
(4) 高速铁路养护维修中应重点关注5 m以下波长的轨道不平顺;为提高乘坐舒适性,有必要对中长波的轨道不平顺进行控制。
[1]LIU Xuewen, XIE Jun, WU Chuan. Semi-Analytical Solution of Vehicle-Bridge Interaction on Transient Jump of Wheel[J]. Engineering Structures, 2008, 30(9): 2401-2412.
[2]娄平,曾庆元. 车辆—轨道—桥梁系统竖向运动方程的建立[J]. 铁道学报, 2004, 26(5): 71-80.
(LOU Ping, ZENG Qingyuan. Formulation of Equations of Vertical Motion for Vehicle-Track-Bridge System[J]. Journal of the China Railway Society, 2004, 26(5): 71-80. in Chinese)
[3]杨宏印,张海龙,陈志军,等. 考虑徐变影响的车—线—桥耦合有限元分析[J]. 中国铁道科学, 2013, 34(6):13-20.
(YANG Hongyin, ZHANG Hailong, CHEN Zhijun, et al. Finite Element Analysis of Train-Track-Bridge Interaction System Considering the Influence of Creep[J]. China Railway Science, 2013, 34(6): 13-20. in Chinese)
[4]LOU Ping, YU Zhiwu, AU F T K. Rail-Bridge Coupling Element of Unequal Lengths for Analysing Train-Track-Bridge Interaction Systems[J]. Applied Mathematical Modelling, 2012, 36(4): 1395-1414.
[5]YANG Hongyin, CHEN Zhijun, ZHANG Hailong. Vibration of Train-Rail-Bridge Interaction Considering Rail Irregularity with Arbitrary Wavelength[J]. International Journal of Engineering, Transaction A: Basics, 2015, 28(4): 516-522.
[6]翟婉明,夏禾. 列车—轨道—桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011.
(ZHAI Wanming, XIA He. Train-Track-Bridge Dynamic Interaction: Theory and Engineering Application[M]. Beijing: Science Press, 2011. in Chinese)
[7]宋国华,高芒芒,黎国清.桥梁墩台不均匀沉降时的车桥垂向系统耦合振动分析[J].中国铁道科学,2010,31(2):29-33.
(SONG Guohua, GAO Mangmang, LI Guoqing. Vehicle-Bridge Vertical System Coupled Vibration Analysis under the Uneven Settlement of Bridge Pier and Abutment[J]. China Railway Science, 2010, 31(2): 29-33. in Chinese)
[8]翟婉明. 车辆—轨道耦合动力学[M]. 北京: 科学出版社, 2007.
(ZHAI Wanming. Vehicle-Track Coupling Dynamics [M]. Beijing: Science Press, 2007. in Chinese)
[9]YANG Hongyin, CHEN Zhijun, LI Shaofan, et al. An Integrated Coupling Element for Vehicle-Rail-Bridge Interaction System with a Non-Uniform Continuous Bridge[J]. Acta Mechanica Solida Sinica, 2015, 28(3): 313-330.
[10]罗浩,郭向荣.多跨斜交简支T梁桥车桥耦合振动分析[J].中国铁道科学,2009,30(4):36-40.
(LUO Hao, GUO Xiangrong. Analysis on the Vehicle-Bridge Coupling Vibration of Multi-Spans Skew Simply-Supported T-Beam[J]. China Railway Science, 2009, 30(4): 36-40.in Chinese)
[11]杨宏印,张海龙,陈志军,等. 考虑瞬时脱离的列车作用下桥梁振动分析[J]. 重庆交通大学学报:自然科学版, 2014, 33(2): 21-25.
(YANG Hongyin, ZHANG Hailong, CHEN Zhijun, et al. Vibration Analysis of Bridge under Trains Considering Transient Jump of Wheel[J]. Journal of Chongqing Jiaotong University:Natural Science, 2014, 33(2): 21-25. in Chinese)
[12]NGUYEN Dinhvan, KIM Kidu, WARNITCHAI Pennung. Simulation Procedure for Vehicle-Substructure Dynamic Interactions and Wheel Movements Using Linearized Wheel-Rail Interfaces[J]. Finite Elements in Analysis and Design, 2009, 45(5): 341-356.
[13]YANG Hongyin, CHEN Zhijun, ZHANG Hailong, et al. Dynamic Analysis of Train-Rail-Bridge Interaction Considering Concrete Creep of a Multi-Span Simply Supported Bridge[J]. Advances in Structural Engineering, 2014, 17(5): 709-720.
