高填明洞土压力计算方法及其影响因素研究

李　盛，马　莉，王起才，李建新，李伟龙，张延杰

(1.兰州交通大学 道桥工程灾害防治技术国家地方联合工程实验室，甘肃 兰州　730070 ；2.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室,甘肃 兰州　730070；3.兰州工业学院 土木工程学院，甘肃 兰州　730050)

随着黄土高原地区经济的不断发展，城市化进程空前加速，加之铁路建设的较高标准线形要求，对城市日趋紧张的土地资源带来了挑战。鉴于黄土高原地区山高、沟深的特点，削山、填沟造地成为了解决这一问题的重要途径，这有力地缓解了城市用地紧张局面，但也不可避免地要对一些既有的或将要新建的铁路明洞进行高回填。由于填土较高，正确计算作用于明洞洞顶土压力是合理设计明洞结构物的关键，也是明洞安全性的保证。否则，一方面，将造成新建明洞结构设计的不合理；另一方面，对于既有明洞，在回填施工期间或竣工后可能出现不同程度的开裂病害，造成铁路运营安全与质量的隐患，增加后期养护维修费用。因此有必要对高填明洞土压力计算方法进行深入研究，并明确各参数对高填明洞土压力大小的影响程度。

国内外对高填方结构物土压力已进行了许多理论及试验研究，主要集中在涵洞(管)上，以各自的理论出发，或根据研究工程对象的不同各持己见，建立了不同的高填涵洞(管)结构土压力计算公式。如Marston以散体极限平衡条件推导的垂直土压力计算方法[1-2]；普罗托基亚可诺夫提出的卸荷拱土压力计算法[3]；忽略应力集中的土柱法；从变形条件出发，以弹性理论解为基础建立的土压力计算法[4-5]；以马斯顿模型为基础，围绕是否考虑等沉面、内外土柱计算面与水平面夹角、内外土柱间摩擦力等3个方面，作不同的假设，推导出不同的土压力计算方法[6-8]。而对于高填明洞土压力的计算方法研究却不足，仅有文献[9，10]研究了高填黄土明洞顶土压力，回归了能够反映明洞垂直土压力变化性状的计算公式。

为了从力学角度得到适合高填黄土明洞土压力的计算方法，本文在已有研究的基础上，基于岩土力学原理，考虑边坡坡角、沟槽宽度等影响因素，建立高填明洞洞顶的土压力计算模型，推导高填明洞洞顶土压力计算公式；以某铁路高填明洞工程为例，通过数值模拟结果和现场实测结果对计算公式进行验证；并进一步通过高填明洞土压力集中系数分析各参数的敏感性。

1　明洞洞顶土压力计算公式推导

对于明洞结构，其刚度大、变形小，而明洞侧面的土体则刚度小、变形大，从而造成等沉面高度以下范围的内土柱沉降量小于两侧外土柱沉降量，故引起明洞洞顶产生附加荷载。同时，边坡也会对外土柱产生向上的摩擦力，减缓附加荷载的增长速度。

1.1　计算模型

基于岩土力学原理，边坡及内土柱分别会对外土柱产生向上的剪切力τ1和τ2，由此建立的明洞洞顶土压力计算模型如图1所示。图1中：H为填土总高度，m；Hc为等沉面高度，m；b为坡脚到明洞侧面的距离，m；D为明洞宽度，m；B为沟槽宽度，m；θ为边坡坡角,(°)；σ1为明洞洞顶土压力，kPa。

图1　明洞洞顶土压力计算模型

为简化推导做以下假设：①按平面应变问题[11-13]考虑；②内、外土柱的分界面为垂直平面，内、外土柱通过该分界面做相对运动，并产生剪切力[4，6，14-15]；③由于填埋结构物侧向土压力的精确计算较为困难，故认为内、外土柱作用力满足朗肯主动土压力理论[6，16-18]；④明洞拱顶弧形影响及土体与明洞之间相互作用忽略不计；⑤外土柱与边坡之间产生摩擦滑移，满足Coulomb定律；⑥洞顶土压力简化为均布荷载。

1.2　洞顶土压力计算公式推导

依据图1所示的计算模型，对明洞洞顶土压力的计算公式推导如下。

1)当H≤Hc时当H≤Hc时，在外土柱深度y处，取微分单元土层dw进行受力分析，其受力计算模型如图2所示。图2中：q为深度y处土压力平均值，kPa；N2为内土柱对外土柱的水平作用力，kN；N3为边坡对外土柱的作用力，kN，h为明洞凸出地面的高度，m。根据图2得到单元土层的受力平衡方程为

qb1+γb1dy=τ2dy+τ1dy+(q+dq)b1

(1)

其中，

b1=b+(H-y)cotθ

式中：b1为边坡到内、外土柱交界处横向宽度，m；γ为填土的平均容重，kN·m-3。

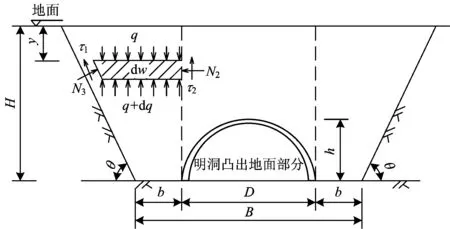
图2　H≤Hc时外土柱受力计算模型

根据朗肯主动土压力理论，内土柱对外土柱的水平作用力N2及边坡对外土柱的作用力N3分别为

(2)

(3)

式中：ka为土侧压力系数；c为填土黏聚力，kPa；δ为边坡与填土之间的摩擦角，(°)，δ取值一般为(1/3～2/3)φ[18]，本文取为1/2φ；φ为填土的内摩擦角(°)。

故边坡与外土柱及内外土柱之间的剪切力τ1和τ2分别为

(4)

τ2=N2tanφ+c

(5)

式中：k0为边坡与土体间的摩擦系数，k0=tanδ。

(b+Hcotθ-ycotθ)dq=(-qα-qk1-β+

γb+γHcotθ-γycotθ+k2)dy

(6)

求解式(6)可得

(7)

式中：C为积分常数项。

为求得常数C，将边界条件y=0，q=0代入式(7)，可得

(8)

将式(8)代入式(7)，并整理后得到外土柱所受的土压力q为

(9)

由此，根据式(5)可得深度y处内外土柱产生的剪切力τ2为

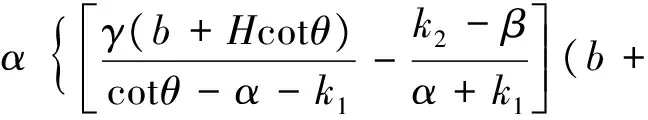
(10)

沿内、外土柱的交界面高度范围内对τ2进行积分，可得深度y处内土柱所受的附加荷载F为

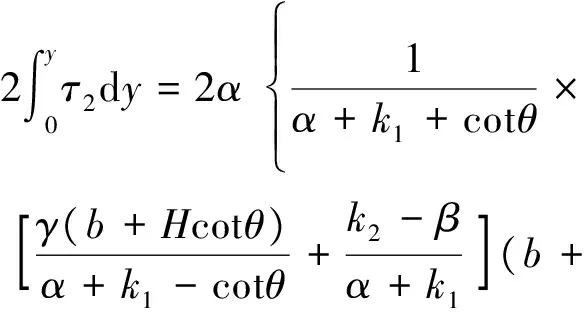
(11)

则深度y处内土柱所受的总土压力σ为

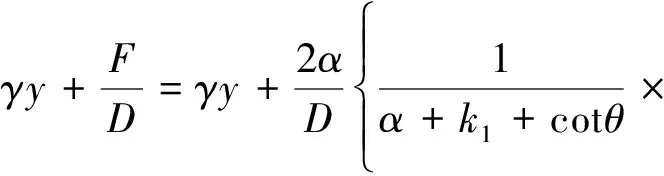
(12)

因此，明洞洞顶土压力σ1为

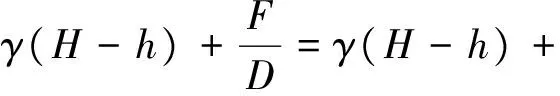
(13)

2)当H>Hc时

当H>Hc时，等沉面Hc以上的内、外土柱没有相对运动，但它们整体相对于两侧边坡而言，有整体向下移动的趋势。故以Hc为分界点，取等沉面上下两部分微分单元土层分别进行受力分析，此时土柱受力的计算模型如图3所示。

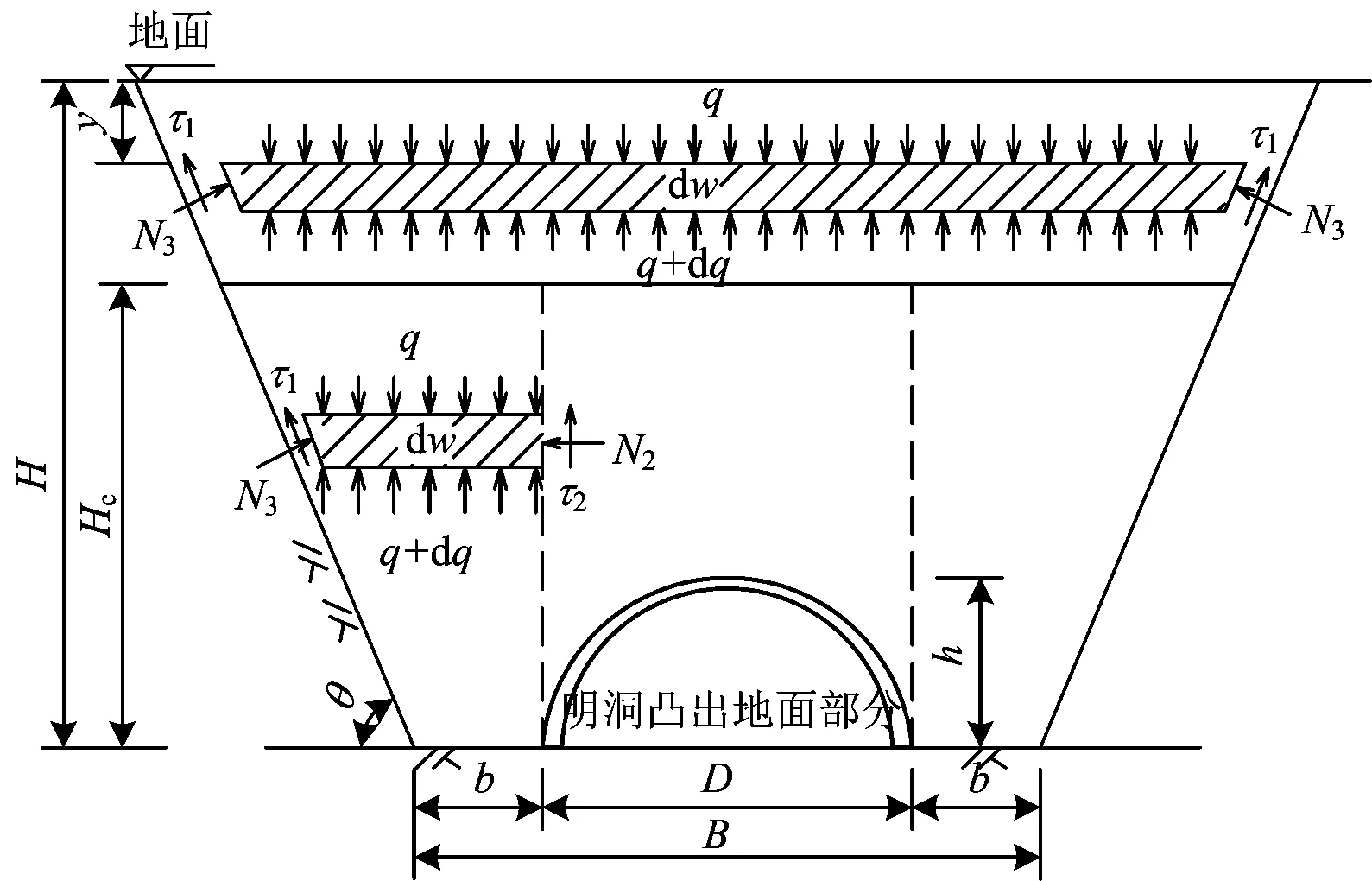
图3　H>Hc时外土柱受力计算模型

(1)Hc以上单元土体所受的土压力

取等沉面Hc以上微分单元土层进行受力分析。根据图3得到单元土体的受力平衡方程为

q[2(H-y)cotθ+B]+γ[2(H-y)cotθ+B]dy=(q+dq)[2(H-y)cotθ+B]+2k0(qka-

(14)

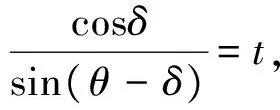
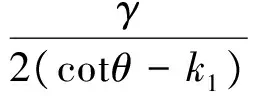
(15)

为求得常数C，将边界条件y=0，q=0代入式(15)，可得

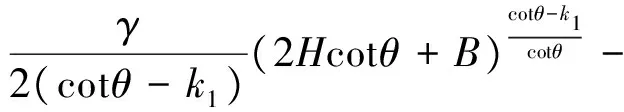
(16)

将式(16)代入式(15)整理后得到等沉面Hc以上土体所受的土压力q为

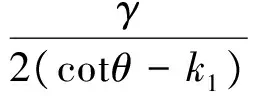
(17)

将y=H-Hc代入式(17)，整理后得到等沉面层Hc高度处土体所受的土压力q为

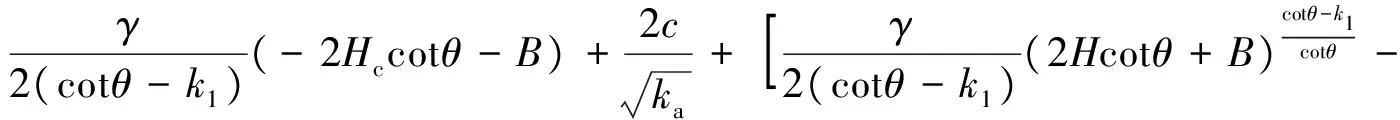
(18)

(2)Hc以下单元土体所受的土压力

与H≤Hc时分析方法相似，取等沉面Hc以上微分单元土层进行受力分析。根据图3得到单元土体的受力平衡方程并求解，所得结果同式(1)—式(7)。

为求常数C，将边界条件y=H-Hc处土压力式(18)代入式(7)得

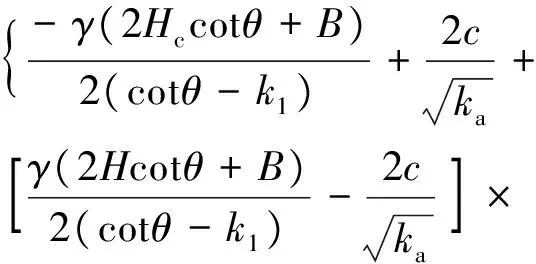
(19)

将式(19)代入式(7)，整理后得到外土柱所受的土压力q为

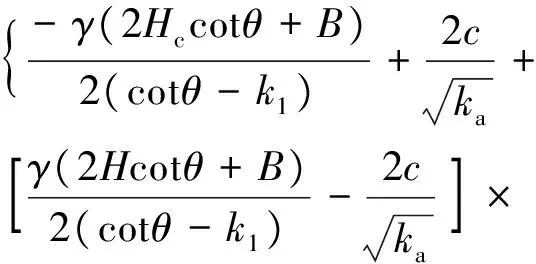
(20)

(3)明洞洞顶土压力

深度y处内外土柱产生的剪切力τ2为

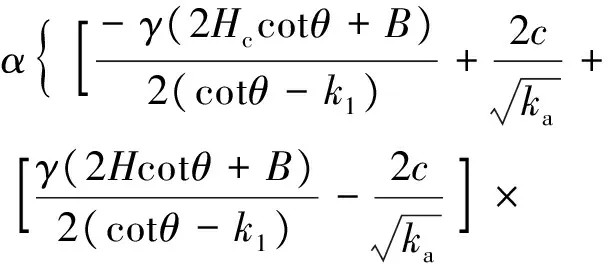
(21)

沿内、外土柱交界面高度范围内对τ2进行积分，可得深度y处内土柱所受的附加荷载F为

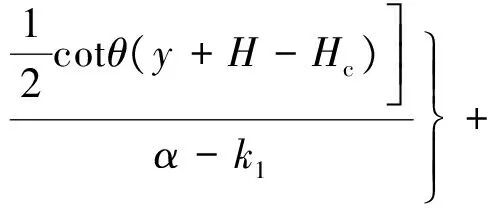
2β(y-H+Hc)

(22)

深度y处内土柱所受的总土压力σ为

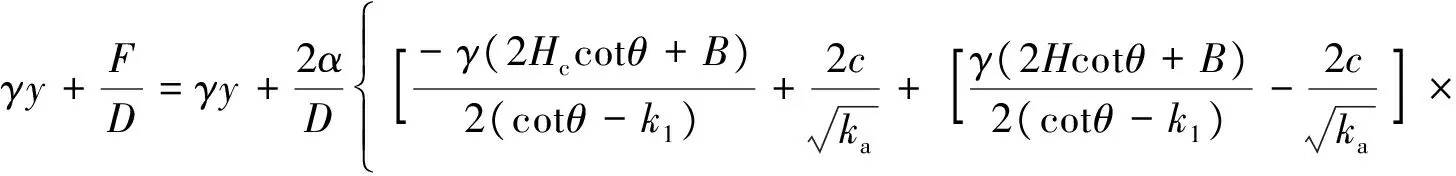
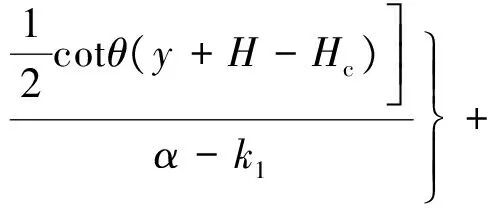
(23)

因此，明洞洞顶土压力σ1为

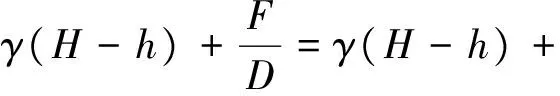
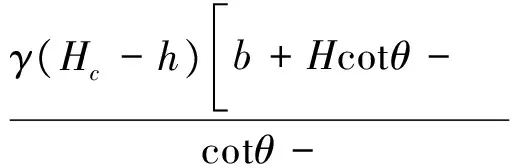
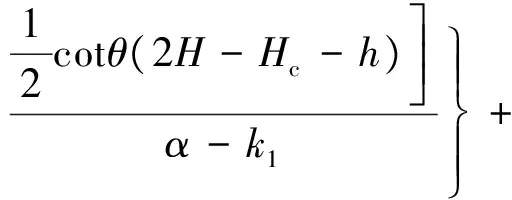
(24)

3) 等沉面高度Hc

根据弹性理论，可以得到内、外土柱的变形量计算公式分别为

(25)

(26)

式中：Δn为内土柱的压缩量，m；Δw为外土柱的压缩量，m；E为土体压缩模量，MPa。

假设内、外土柱的土体压缩模量相同[12]，则由变形条件Δw=Δn，可得到等沉面高度Hc的计算公式。

2　公式验证

以文献[9-10]中铁路高填黄土明洞工程为例，采用上文推导的式(13)、式(24)—式(26)计算明洞洞顶土压力，并利用有限元进行模拟分析。通过对比明洞洞顶土压力的本文推导公式计算结果、有限元计算结果、现场实测结果，评估计算方法的正确性。

在有限元建模过程中，明洞、边坡均采用理想线弹性模型；填土选取理想弹塑性Mohr-Coulomb模型；明洞、边坡与土的接触关系均采用Coulomb定律实现，即τcrit=μp，其中τcrit为极限剪应力，μ为摩擦系数，p为法向接触应力[19]。模型两侧定义水平方向的边界约束，底部定义水平和竖直方向的约束。通过定义时间步的方法模拟分层填筑过程，计算每个时间步的应力场、位移场。材料计算参数见表1。

表1　计算参数

明洞洞顶土压力本文计算结果、有限元模拟结果和现场实测结果随填土高度变化规律如图4所示。由图4可知：当填土高度较低(小于5 m)时，本文计算结果、有限元模拟结果与现场实测结果基本一致；当填土高度大于5 m时，有限元计算结果>本文计算结果>实测结果，其中本文计算结果与有限元模拟结果的最大相对误差为11.3%，与现场实测结果的最大相对误差为16.5%；这可能是由于在明洞实际填土压实过程中，为了避免振动压路机对明洞结构的破坏，使洞顶的压实系数低与明洞两侧的压实系数，随着填土高度的增加，产生了土拱效应，造成明洞实测土压力的减小；而在本文计算公式中和有限元模拟中，均采用统一的填土压实系数，因此外土柱沉降大于内土柱，从而造成洞顶应力的集中。由此验证了本文计算方法的正确性。

图4　明洞洞顶土压力随填土高度变化规律

3　影响参数分析

为了明确影响高填明洞洞顶土压力参数的敏感性，方便设计者合理安排及指导现场实践，采用明洞洞顶土压力集中系数(σ1/rh)分析边坡坡角θ、填料性质(填料内摩擦角φ，黏聚力c)、明洞高宽比h/D、沟槽与明洞宽度比B/D等参数对明洞洞顶土压力的影响程度。

基本参数取值：明洞洞顶填土高度H=5，10，…，35 m，边坡坡角θ=50°，填料内摩擦角φ=24°，黏聚力c=25 kPa，压缩模量E=8 000 kPa，B/D=1.1，h/D=0.4。

3.1　边坡坡角的影响

边坡坡角θ=50°，60°，70°，80°时，明洞洞顶土压力集中系数随填土高度的变化曲线如图5所示。取明洞洞顶填土高度H=25，35 m，等沉面高度随边坡坡角变化的曲线如图6所示。

图5不同边坡坡角时明洞洞顶土压力集中系数随填土高度变化曲线

由图5可知：随着填土高度的增加，边坡坡角对明洞洞顶土压力的影响越来越显著，且坡角越小，明洞洞顶土压力集中系数越大；当填土高度H=5 m，坡角从50°增大到80°时，土压力集中系数从1.19减小到1.16，变化不明显，但当填土高度H增加到35 m，坡角从50°增大到80°时，土压力集中系数从1.43减小到1.17，减小了18%。这是由于随着填土高度的增加，边坡坡角的增大增强了边坡对土体的上托作用，减缓洞顶土压力的增长趋势。

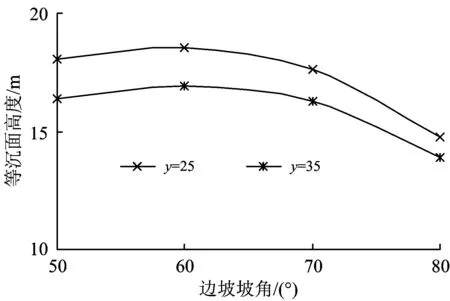
图6　不同填土高度时等沉面高度随边坡坡角变化曲线

由图6可知：等沉面高度随着填土高度的增大而减小，随着边坡坡角的增大，先增大后减小；当坡角从50°增大到80°时，填土高度为25 m时等沉面高度由18.04 m减小到17.03 m；填土高度为35 m时等沉面高度由16.40 m减小到13.90 m。

3.2　填料性质的影响

1)内摩擦角φ

填料内摩擦角φ=10°，20°，30°，40°时，明洞洞顶土压力集中系数如图7所示。由图7可知：当填土高度较低(H<10 m)时，土压力集中系数随着内摩擦角的增大逐渐减小，且随着填土高度的增大而增大；当填土高度10 m≤H<25 m时，土压力集中系数随着内摩擦角的增大而增大，且随着填土高度的增大而增大；当填土高度H≥25 m时，土压力集中系数随着内摩擦角的增大而减小，且随着填土高度的增大而减小；随着摩擦角从10°增加到40°，当填土高度为5 m时，土压力集中系数从1.22增加到1.15；当填土高度为15 m时，土压力集中系数从1.35增加到1.45；当填土高度为35 m时，土压力集中系数从1.43减小到1.39。

图7不同内摩擦角时明洞洞顶土压力集中系数随填土高度变化曲线

2)黏聚力c

黏聚力c=20，30，40，50 kPa时，明洞洞顶土压力集中系数见表2。由表2可知：填土高度一定时，黏聚力越大，土压力集中系数就越大；随着黏聚力从20 kPa增加到50 kPa，当填土高度为5 m时，土压力集中系数从1.18增加到1.24；当填土高度为35 m时，土压力集中系数从1.42增加到1.47。

表2　不同黏聚力时明洞洞顶土压力集中系数

3.3　明洞高宽比h/D、沟槽与明洞宽度比B/D的影响

明洞高宽比h/D=1.0，1.5，2.0，2.5时，明洞洞顶土压力集中系数随填土高度变化曲线如图8所示。沟槽与明洞宽度比B/D=0.4，0.6，0.8，1.0，1.2时，明洞洞顶土压力集中系数随填土高度变化曲线如图9所示。

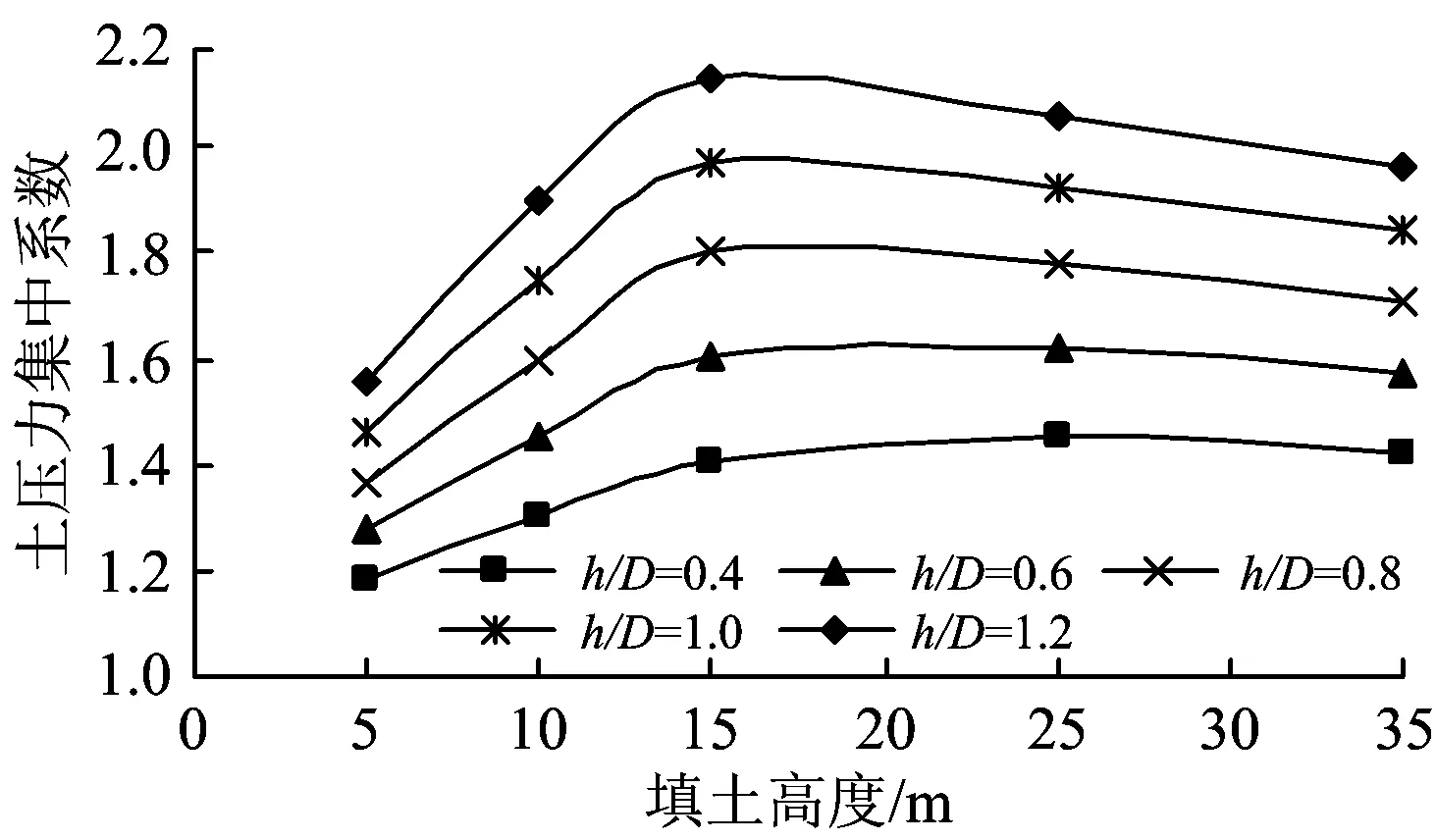
图8　不同高宽比时明洞洞顶土压力集中系数变化曲线

图9不同沟槽与明洞宽度比时明洞洞顶土压力集中系数变化曲线

由图8可知：随着填土高度的增加，不同h/D的明洞洞顶土压力集中系数均先增大后减小；当填土高度为35 m时，随着h/D从0.4增加到1.2，土压力集中系数从1.42增大到1.84(明洞洞顶土压力从831.6 kPa增大到1 151.5 kPa)。这是由于：h/D越大，相对明洞竖向变形而言，明洞高度范围内两侧低压实土体可变形量就越大，等沉面高度越大，对中间土柱产生的向下剪切力就越大，从而作用在明洞洞顶土压力集中系数增大。

从图9可以看出：随着填土高度的增加，不同B/D的明洞洞顶土压力集中系数均先增大后减小，且B/D越大，作用在明洞洞顶的土压力越大；当填土高度为35 m时，随着B/D从1.0增大到2.5时，土压力集中系数从1.39增大到1.78(明洞洞顶土压力从816.7 kPa增大到1 045.4 kPa)。这是由于：内外土体的总宽度和总重力增加，边坡对其上托作用相对减弱，外土柱的下沉量增加，使洞顶平面上，内、外土柱的沉降差加大；同时，等沉面高度由15.5 m增大到27.4 m，引起作用在明洞洞顶土压力增大，土压力集中系数随之增大；而当填土高度等于初始等沉面高度时，内外土体沉降差为零，之后随着填土高度的增加，边坡作用效应的增强使附加荷载逐渐减小，土压力集中系数随之减小。

4　结　论

(1)基于岩土力学原理，考虑边坡坡角、沟槽宽度等影响因素，推导了高填黄土明洞洞顶土压力的计算公式；通过1个实例的计算结果，并与有限元模拟结果和现场实测结果进行对比，验证了本文计算方法的正确性。

(2)等沉面高度随着填土高度的增大而减小，随着边坡坡角的增大而先增大后减小。

(3)随着填土高度的增加，土压力集中系数先增大后减小，边坡坡角的影响逐渐显著；明洞高宽比、沟槽与明洞宽度比越小，边坡坡角越大，高填明洞洞顶土压力越小。相比而言，填料内摩擦角、黏聚力对明洞洞顶土压力的影响不明显；因此，工程实际中，应尽可能减小明洞高宽比、沟槽与明洞宽度比，同时在保证边坡稳定的前提下，提高回填边坡坡角。

[1]MARSTON Anson. The Theory of External Loads on Closed Conduits in the Light of the Latest Experiments[C]//Highway Research Board Proceedings. Washington D C：Transportation Research Board，1930, 138-170.

[2]MASTON A, ANDSERSON A O. The Theory of Loads on Pipes in Ditches and Tests of Cement and Clay Drain Tile and Sewer Pipe[R]. Iowa: Iowa Engineering Experiment Station Bulletin, Iowa State College, Ames, 1913: 31-181.

[3]R K 克列因.散粒体结构力学[M]. 陈万佳，译. 北京: 中国铁道出版社: 1983.

[4]顾安全. 上埋式管道及洞室垂直土压力的研究[J]. 岩土工程学报, 1981, 3(1)：3-15.

(GU Anquan. Vertical Earth Pressure on Top-Buried Pipes and Caves[J]. Chinese Journal of Geotechnical Engineering, 1981, 3(1): 3-15.in Chinese)

[5]王晓谋, 顾安全. 上埋式管道垂直土压力的减荷措施[J]. 岩土工程学报, 1990, 12(3): 83-89.

(WANG Xiaomou, GU Anquan. Research on Methods of Vertical Earth Pressure Reduction on Top-Buried Pipes[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(3): 83-89. in Chinese)

[6]曾国熙. 土坝下涵管竖向土压力的计算[J]. 浙江大学学报, 1960 (3): 79-97.

(ZENG Guoxi. The Vertical Earth Pressure on Culvert under the Dam[J]. Journal of Zhejiang University, 1960 (3): 79-97. in Chinese)

[7]CHEN R P, CHEN Y M, LING D S. Analysis of Vertical Pressure on Buried Pipeline with Case Study[J]. Journal of Zhejiang University：Science, 2000, 1(4): 414-420.

[8]娄奕红, 王秉勇. 涵洞顶填土压力的计算分析[J]. 岩土力学, 2003, 24(3): 475-478.

(LOU Yihong, WANG Bingyong. Analysis of Earth Pressure on Top of Culverts[J]. Rock and Soil Mechanics, 2003, 24(3): 475-478. in Chinese)

[9]李盛, 王起才, 马莉, 等. 高填土明洞土压力减载计算[J]. 华中科技大学学报：自然科学版, 2013, 41(11): 58-63.

(LI Sheng, WANG Qicai, MA Li，et al. Calculating Load Reduction of Earth Pressure on High Fill Open Cut Tunnel[J]. Journal of Huazhong University of Science and Technology：Natural Science Edition, 2013, 41(11): 58-63. in Chinese)

[10]赵鹏, 王起才, 李盛, 等. 明洞顶垂直土压力性状及土工格栅减载方案研究[J]. 兰州交通大学学报, 2013, 32(4): 79-84.

(ZHAO Peng, WANG Qicai, LI Sheng, et al.Study on Vertical Loess Pressure Properties and the Load Shedding Scheme of Geogrid of Myeong-Dong[J]. Journal of Lanzhou Jiaotong University, 2013, 32(4): 79-84. in Chinese)

[11]杨锡武, 张永兴. 公路高填方涵洞土压力变化规律及计算方法研究[J]. 土木工程学报, 2005, 38(9): 119-124.

(YANG Xiwu, ZHANG Yongxing. A Study on the Earth Pressure Theory for High Fill Culverts[J]. China Civil Engineering Journal, 2005, 38(9): 119-124. in Chinese)

[12]李永刚, 李珠, 张善元. 矩形沟埋涵洞顶部垂直土压力[J]. 工程力学, 2008, 25(1): 155-160.

(LI Yonggang, LI Zhu, ZHANG Shanyuan. Earth Pressure on the Top of Rectangular Trench-Buried Culverts[J]. Engineering Mechanics, 2008, 25(1): 155-160. in Chinese)

[13]郑俊杰, 赵建斌, 陈保国. 高路堤下涵洞垂直土压力研究[J]. 岩土工程学报, 2009, 31(7): 1009-1013.

(ZHENG Junjie, ZHAO Jianbin, CHEN Baoguo. Vertical Earth Pressure on Culverts under High Embankments[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1009-1013. in Chinese)

[14]田文铎. 地下管垂直土压力计算探讨[J]. 水利水电技术, 1994(2): 9-14.

(TIAN Wenduo.A Discussion on Computation of Vertical Soil Pressure Acting on Buried Pipes[J]. Water Resources and Hydropower Engineering, 1994 (2): 9-14. in Chinese)

[15]申文明, 边学成, 唐晓武，等. 低填方上埋式管涵土压力的模型试验和理论研究[J]. 岩土工程学报, 2010, 32(7): 1017-1022.

(SHEN Wenming, BIAN Xuecheng, TANG Xiaowu, et al. Model Tests and Theoretical Studies on Earth Pressure on Shallow Positive Buried Culverts[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 1017-1022. in Chinese)

[16]刘静. 高填路堤涵洞土压力理论及减荷技术研究[D]. 西安: 长安大学, 2004.

(LIU Jing. Study on the Earth Pressure Acting on the Culvert under the Embankment of High-Staked Soil and the Load Reducing Technique[D]. Xi’an: Chang’an University, 2004. in Chinese)

[17]郑俊杰, 马强, 张军. 加筋减载涵洞的涵顶土压力计算[J]. 岩土工程学报, 2011, 33(7): 1135-1141.

(ZHENG Junjie, MA Qiang, ZHANG Jun. Calculation of Vertical Earth Pressure on Load Reduction Culverts under Embankments by Reinforcement[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(7): 1135-1141. in Chinese)

[18]陈仲颐, 周景星, 王洪瑾. 土力学[M]. 北京: 清华大学出版社, 1994.

(CHEN Zhongyi, ZHOU Jingxing, WANG Hongjin. Soil Mechanics[M]. Beijing: Tsinghua University Press, 1994. in Chinese)

[19]郑俊杰, 陈保国, 张世飚. 沟埋式涵洞非线性土压力试验研究与数值模拟[J]. 岩土工程学报, 2008, 30(2): 1771-1777.

(ZHENG Junjie, CHEN Baoguo, ZHANG Shibiao. Experimental Investigation and Numerical Simulation of Nonlinear Earth Pressure for Trench-Buried Culverts[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 1771-1777. in Chinese)