列车—轨道—桥梁耦合系统动力方程求解方法对计算精度和效率的影响

朱志辉,龚　威，王力东，蔡成标，余志武

(1.中南大学 土木工程学院，湖南 长沙　410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙　410075；3.西南交通大学 牵引动力国家重点实验室，四川 成都　610031)

随着列车的高速化和重载化，列车在桥梁上行驶时引起的桥梁动力响应及其对行车安全性和乘坐舒适性的影响是近20年内的重要研究内容[1]。同时，大跨度桥梁在我国高速铁路线路中的应用日益增多[2]，提高车—桥耦合振动分析(Train-bridge coupled analysis，TBA)的计算效率和计算精度对于全面和深入分析大跨度桥梁动力响应和行车安全性至关重要[3]。Doménech[4]，Pablo[5]和Lou[6-7]分别对比和讨论了不同车辆模型、不同轮轨关系以及不同桥梁模型对TBA计算精度的影响。但关于不同车—桥耦合系统动力方程求解方法对计算精度和计算效率的研究还不充分。

目前在车—桥耦合系统动力方程求解方法中，根据车辆和桥梁子系统动力方程求解过程中是否在每个时间步上进行迭代求解计算，可分为分离迭代计算方法(the separation and iteration method, SIM)和耦合时变计算方法(the coupled and time-dependent method, CTM)[1]2类。其中SIM将车辆和桥梁作为2个独立的子系统，分别求解车辆和桥梁动力方程，但是2个子系统需要在每一时间步内进行迭代求解，直至满足轮轨接触点处力平衡条件和位移协调条件。在整个计算过程中，由于SIM中的车辆和桥梁子系统的质量、刚度和阻尼矩阵为常量，从而简化了理论推导及求解难度[3]，且易于和现有有限元软件相结合[8]，在以往的研究中得到了较为广泛应用[9-12]。CTM直接建立车辆和桥梁耦合系统整体时变动力方程，在每一时间步通过直接法求解动力方程[13-15]。CTM虽然可以避免SIM在每一时间步内的收敛迭代计算，但需要在每一时间步根据移动的轮轨接触点实时更新时变系统阻尼和刚度矩阵[13]。当车辆模型复杂以及存在大量轮轨接触点时，将会导致推导时变系统刚度和阻尼矩阵非常复杂，从而限制了该方法在铁路桥梁的车—桥耦合振动研究中使用[7，16]。

在过去的很多车—桥耦合振动研究中，通常假定钢轨与桥面之间无相对运动，忽略轨道结构的弹性变形[8，11]。随着研究的逐步深入，轨道结构的弹性支承和变形作用在车—桥耦合振动中的影响逐步引起了研究人员的重视[7，12]。但当在车—桥耦合振动研究中考虑轨道结构时，会使以往不突出的问题变得重要，比如计算效率、收敛性和计算精度问题。吴定俊[12]、杜宪亭[17]等分别针对轮轨分离模型和密贴模型，讨论了分离迭代算法的数值求解稳定性问题。虽然轮轨分离模型在足够小的时间积分步长下可以收敛，但会导致计算时间过长。同时，当在研究车—桥耦合振动中考虑钢轨时，由于簧下车轮质量大于轮轨接触点处钢轨质量，从而导致密贴模型计算不收敛。为提高SIM的计算收敛性，Zhang[18]提出全过程迭代法求解车—桥耦合系统动力方程，杜宪亭[11]提出基于精细Rung-Kutta混合积分法的车—桥耦合振动非迭代求解算法；但上述研究并未考虑轨道结构，且未给出不同方法对于轮轨力、钢轨振动加速度计算精度的影响。

鉴于SIM和CTM在车—桥耦合系统动力分析过程中各自的优势与缺点，以及考虑轨道结构以后的列车—轨道—桥梁耦合系统(train-track-bridge couples system，TTBCS)的复杂性，本文基于轮轨Hertz接触模型，分别采用SIM与CTM建立了TTBCS垂向动力方程，并编写了2种计算方法的MATLAB程序。首先根据谱半径理论和最大频率讨论2种方法对时间积分步长的要求以及在计算收敛性方面的差别；然后以8辆车编组的高速列车通过5跨简支梁桥为例，对比2种方法的计算精度，并讨论不同积分时间步长对车体、钢轨和桥梁动力响应以及轮轨力等指标计算精度的影响，从而为TTBCS动力分析选择合理的分析方法和确定合理的时间积分步长提供参考。

1　车辆—轨道—桥梁耦合系统模型

图1为典型的列车—轨道—桥梁耦合系统垂向动力相互作用模型示意图，该系统包括车辆子系统和轨道—桥梁子系统两部分，2个子系统之间通过轮轨相互作用联系在一起；当不考虑外部激励时，轨道不平顺是引起二者振动的激励源。图中，m，c和k分别为质量、阻尼和刚度，z为沉浮位移，θ为点头位移，下标c,b,w,p和s分别表示车体、转向架、轮对、一系悬挂、二系悬挂。

图1　列车—轨道—桥梁耦合系统示意图

1.1　车辆子系统模型

通常一列列车由Nv节车辆组成，当忽略车体局部变形时，每节车辆可以简化为由1个车体、2个转向架、4个轮对以及一系和二系悬挂组成的质量—弹簧—阻尼器系统。由于考虑了轨道结构，密贴模型会使得分离迭代法计算难以收敛或计算精度下降(采用虚拟质量法保证其收敛性)[5]，因此本文采用轮轨Hertz接触模型。每节车共有10个自由度，包括车体、转向架的沉浮(zcj,zb1j,zb2j) 和点头(θcj,θb1j,θb2j)以及轮对的沉浮(zw(4j-3)，zw(4j-2)，zw(4j-1)，zw4j)。根据多刚体假定和线性悬挂系统假定，每节车的参数可以简化为一系悬挂刚度和阻尼(kp,cp)、二系悬挂刚度和阻尼(ks,cs)、车体的质量和点头转动惯量(mc,Jc)、构架的质量和点头转动惯量(mb,Jb)以及轮对的质量mw。

当列车匀速运行时，不考虑车辆之间的纵向相互作用，采用D’Alembert原理，可建立基于平衡位置的车辆子系统运动方程

(1)

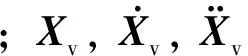
车辆子系统质量矩阵为

(2)

其中，

Mvj=diag(mcJcmbJbmbJbmwmwmwmw)

式中：Mvj为第j节车的质量矩阵。

车辆子系统刚度矩阵为

(3)

式中：Kvj为第j节车的刚度矩阵，其具体表达式可参考文献[7]。

第j节车的阻尼矩阵Cvi与Kvi在形式上相同，只需将Kvi中的一系悬挂刚度kp与二系悬挂刚度ks替换成一系悬挂阻尼cp与二系悬挂阻尼cs即可。

车辆子系统位移向量Xv为

(4)

式中：Xvj为第j辆车的位移向量。

10个自由度垂向车辆模型的位移向量为

Xvj=(zcjθcjzb1jθb1jzb2jθb2jzw(4j-3)zw(4j-2)zw(4j-1)zw4j)

(5)

1.2　轨道—桥梁模型

在车—桥耦合振动分析中，轨道结构不但对桥梁动力特性有影响[19]，而且考虑轨道结构可以更准确地评估行车安全性和乘坐舒适性[20]。同时，以往的研究发现，模态叠加法虽然可以提高结构动力响应的计算效率，但是很难准确体现钢轨的局部高频振动特性。因此，本文采用有限元方法建立轨道—桥梁子系统模型，并采用直接刚度法建立轨道—桥梁子系统动力平衡方程

(6)

式中：Mb,Cb和Kb分别为轨道—桥梁系统的总体质量矩阵、总体阻尼矩阵和总体刚度矩阵；Xb和Fb分别为轨道—桥梁系统的位移向量和荷载向量。

1.3　轮轨接触模型

车辆子系统和桥梁子系统之间的动力相互作用通过轮轨接触实现，同时轮轨之间的相互作用也是引起 2个子系统振动的主要激励源。现在处理轮轨接触主要有2种方法[21]：一种是忽略轮轨相对变形的密贴模型[6,7,22]，另一种是考虑轮轨相对变形的Hertz接触模型[8,12]。密贴模型虽然理论上较为简单，但是当在车—桥耦合振动中考虑轨道结构时，由于轮轨接触点处轮对质量大于钢轨质量，容易导致计算难以收敛[12]，需要采用虚拟质量法进行特殊处理以改善收敛性[17]。本文采用基于切线斜率法的线性赫兹接触模型模拟轮轨接触关系[3]。切线斜率法是指过非线性赫兹接触曲线中静态轮轨力P0对应的点作切线，切线的斜率即为轮轨接触弹簧刚度kh的取值。根据非线性赫兹接触理论，轮轨垂向作用力P(t)与轮轨弹性压缩量δZ(t)之间有如下关系：

(7)

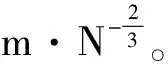
将式(7)两端对δZ(t)求导， 并将静态轮轨力P0对应的轮轨静压缩量δZ0(t)代入式(7)，即可得kh的取值

(8)

2　车辆—轨道—桥梁系统耦合时变动力方程

车辆—轨道—桥梁系统耦合时变动力方程将车辆子系统动力方程(1)和轨道—桥梁子系统动力方程(6)通过轮轨接触关系视为1个整体，系统耦合时变动力方程可写为

(9)

式中：Ksystem为系统的整体刚度矩阵。

由于轮轨接触模型中只包括刚度项，不包括阻尼项和质量项，因此车辆子系统与桥梁子系统的耦合项只体现在耦合系统刚度矩阵中。耦合系统的质量矩阵和阻尼矩阵由车辆子系统和轨道—桥梁子系统的质量和阻尼矩阵按主对角排列形成。

耦合系统总刚度矩阵Ksystem可表示为

Ksystem=K1+K2

(10)

式中：K1为车辆子系统与桥梁子系统不考虑耦合项的整体刚度矩阵；K2为车辆与钢轨的接触矩阵。

在整个计算过程中K1保持不变。K1可由Kv和Kb按主对角排列形成

(11)

若上桥的轮对数为Nob，则K2可表示为

(12)

式中：K2i为桥上第i个轮对与轨道的接触刚度矩阵，需要在每一时间步根据列车轮轨位置实时更新。

根据列车已运行时间、列车初始位置与运行速度可知第i个轮对所在的轨道单元n及在单元上的相对位置xi，如图2所示。图中n和n+1为单元n的2个节点；zrn和θrn分别为第n个节点的竖向位移与转角位移；zr(n+1)和θr(n+1)分别为第n+1个节点的竖向位移与转角位移。

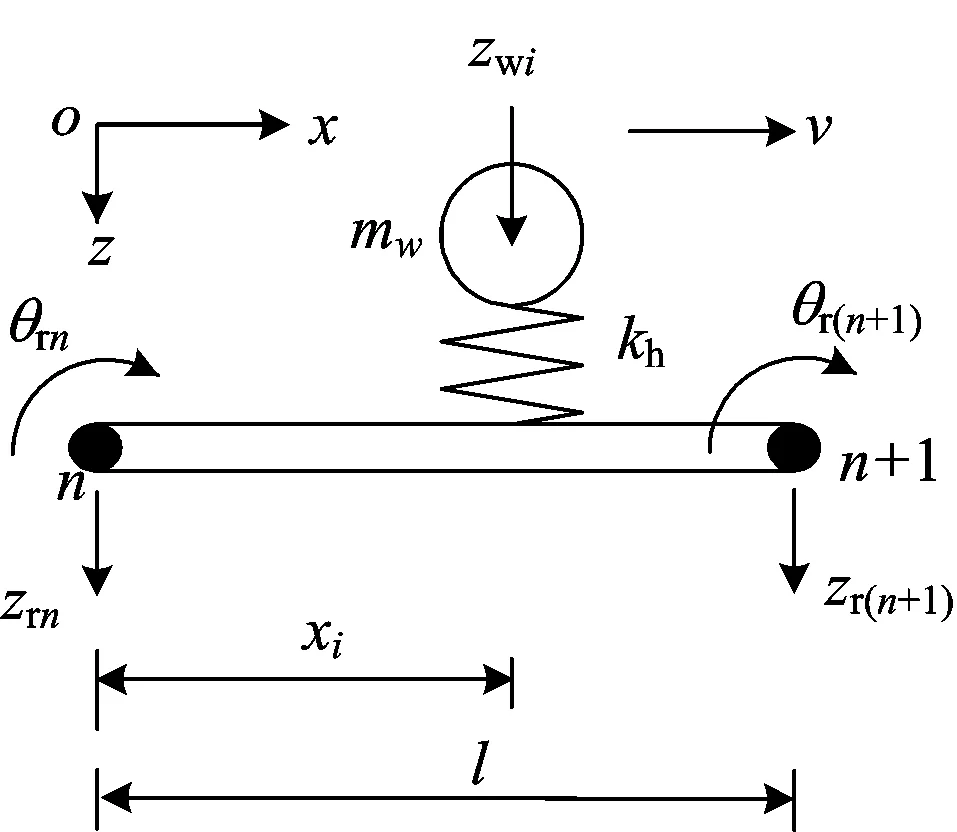
图2　第i个轮对与轨道单元耦合示意图

由于系统只考虑垂向振动，故只将轮对的竖向自由度zw与轨道单元节点的竖向自由度zr及转角自由度θr耦合。K2i可表示为

(13)

其中，kii=khkiq=-khN(x)|x=xi

式中：0为零矩阵或零向量；N(x)为钢轨单元的形函数向量，本文采用Hermit三次多项式作为梁单元形函数[7]。

式(9)等号右端为耦合时变系统的整体荷载向量，其中车辆荷载列向量可表示为

Fv=Fvg+Fvr

(14)

其中，

Fvgi=(mcg0mbg0mbg0mwgmwg

mwgmwg)

Fvri=(0khr(x)0)T|x=xi

式中：Fvg为车辆的重力荷载：Fvgi为第i辆车的重力荷载向量；Fvr为车辆所受轨道不平顺激励；Fvgi为第i个轮对受到的轨道不平顺激励，是(10×Nv)×1的列向量；r(x)为轨道不平顺，由轮对在轨道上的位置决定。

需要指出的是，在Fvgi中，除了第i个轮对所对应的自由度位置外，其余位置均为零。

桥梁的荷载列向量Fb可表示为

(15)

其中，

Fbri=-khr(x)(0N(x)0)T

式中：Fbr为桥梁所受轨道不平顺激励；Fbri为桥上第i个轮对所在位置的轨道单元受到的不平顺激励，是1个Nb×1的列向量，Fbri中除了单元n对应的自由度位置外，其余位置均为零。

3　车辆—轨道—桥梁系统分离迭代动力方程

采用分离迭代法时，直接将车辆子系统动力方程(1)和轨道—桥梁子系统动力方程(6)写为矩阵形式，即可得到耦合系统整体动力方程

(16)

与式(9)相比，式(16)等号左端项中没有车辆子系统和轨道—桥梁子系统之间的耦合项，车辆子系统和轨道—桥梁子系统之间通过轮轨相互作用平衡条件的反复迭代实现动力平衡，从而保证在整个迭代分析过程中，无需根据车辆位置改变耦合系统的质量、刚度和阻尼矩阵。

式(16)中的车辆荷载列向量可写为

(17)

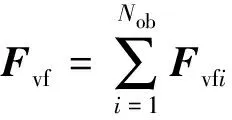
Fvfi=(0kh(zrwi-zwi)0)T

式中：Fvf为车辆受到的由轮轨压缩量引起的轮轨力；Fvfi为在桥上的第i个轮对所受由轮轨压缩量引起的轮轨力，在每一时间步中，可根据桥上第i个轮对与所在位置钢轨的运动状态(见图2)确定；zrwi-zwi为第i个轮对所在位置的轮轨压缩量，zwi为第i个轮对所在位置的钢轨竖向位移。

zrwi可以由钢轨单元节点位移及其形函数求得

zrwi=XnNT(x)|x=xi

(18)

式中：Xn为轮对下钢轨单元位移向量。

桥梁荷载列向量为

Fb=Fbr+Fbf

(19)

其中，

(0N(x)0)T|x=xi

式中：Fbf为桥梁受到的由轮轨压缩量引起的轮轨力；Fbfi为第i个轮对处由轮轨压缩量引起的轮轨力。

4　SIM和CTM计算流程

图3给出了TTBCS采用SIM和采用CIM的计算流程，其中T为总计算时间，t为每步计算时间，Δt为时间积分步长。

图3　车—轨—桥系统求解流程图

需要指出的是，在CTM中，只有接触刚度矩阵K2及车辆与桥梁所受轨道不平顺激励(Fvr,Fbr)是随时间变化的，必须在每一时间步根据车辆位置重新计算。在SIM的迭代收敛判断中，要求在任一时间步内第k迭代步的运动状态与第k+1步的运动状态满足迭代收敛准则。由于轮轨间相互作用力体现了车辆与桥梁2个子系统的响应状态及耦合关系，本文以轮轨力相对误差百分比ε≤10-6作为收敛判断准则[23]。

5　时间积分步长及迭代计算稳定性

时间积分步长和迭代计算稳定性是动力方程求解过程中的2个关键问题，需要从计算精度和效率进行综合考虑[24]。本文通过图4所示的列车—轨道—桥梁耦合系统简单模型，分别对TTBCS的时间积分步长和迭代计算稳定性进行讨论。

图4　列车—轨道—桥梁耦合系统简化模型

5.1　时间积分步长

时间积分步长是决定动力方程求解精度的重要参数，根据Clough & Penzien建议[24]，时间积分步长Δt≤1/(10fmax) ，其中fmax为系统最高自振频率。TTBCS属于刚柔组合的复杂系统，其中车辆及轨道—桥梁子系统以低频振动为主；轮轨相互作用则以高频振动为主(轮轨间接触刚度较大)[12]。

依据一般车辆参数，假定简化模型的计算参数为：mc=5 750 kg,mw=1 000 kg,mr=36 kg,kp=2 MN·m-1,cp=80 kN·s·m-1,kr=47.6 MN·m-1,cr=75 kN·s·m-1,kh=1.44 GN·m-1。可求得图4所示简化模型振动系统的fmax=1 040.2 Hz，从而可以确定最大时间积分步长Δtmax≤0.104 ms。

5.2　迭代稳定性讨论

对于耦合时变动力方程，其积分稳定性主要由数值积分方法决定。当采用无条件稳定的积分方法(如Newmark-β法)时，耦合时变动力方程不存在迭代收敛性问题。当采用分离迭代方法时，由于车辆子系统和轨道—桥梁子系统之间存在时间积分步内的迭代，其积分稳定性除了受积分方法的影响外，还受到迭代计算的影响。故本文利用谱半径理论[17]研究分离迭代法的迭代稳定性(本文仅对Newmark-β法进行讨论)。

按照参考文献[17]对谱半径的推导过程，可得图4所示简化模型的迭代矩阵的谱半径为

(20)

由式(20)可知，谱半径主要由积分步长决定。为使得分离迭代法在积分步内的迭代收敛，则谱半径必须小于1，而且考虑到迭代收敛速度，对谱半径的要求则更高。根据5.1节中的参数，图5给出了谱半径随时间积分步长Δt的变化曲线。由图5可知，当R<1时，Δt<0.37 ms。

图5　谱半径随积分步长变化曲线

6　算　例

以8辆车编组(1M+6T+1M)的CRH2型高速列车通过5跨32 m预应力混凝土简支箱梁桥为例，对比SIM和CTM在TTBCS系统动力响应计算精度和计算效率上的区别。车辆参数可参考文献[25]，主梁和桥墩截面如图6所示。采用有限元法建立的轨道—桥梁子系统模型如图7所示(图中A点和B点为第3跨跨中钢轨和梁体位置)，其中主梁、桥墩和钢轨均采用梁单元模拟，钢轨和主梁之间通过刚臂考虑线路偏心[3]。钢轨节点和刚臂节点之间通过弹簧—阻尼器连接，考虑轨下扣件和垫板的弹性支撑作用，其垂向刚度和阻尼分别取47.6 MN·m-1和75 kN·s·m-1。轨道不平顺谱采用我国高速铁路无砟轨道不平顺谱，车辆时速为300 km。

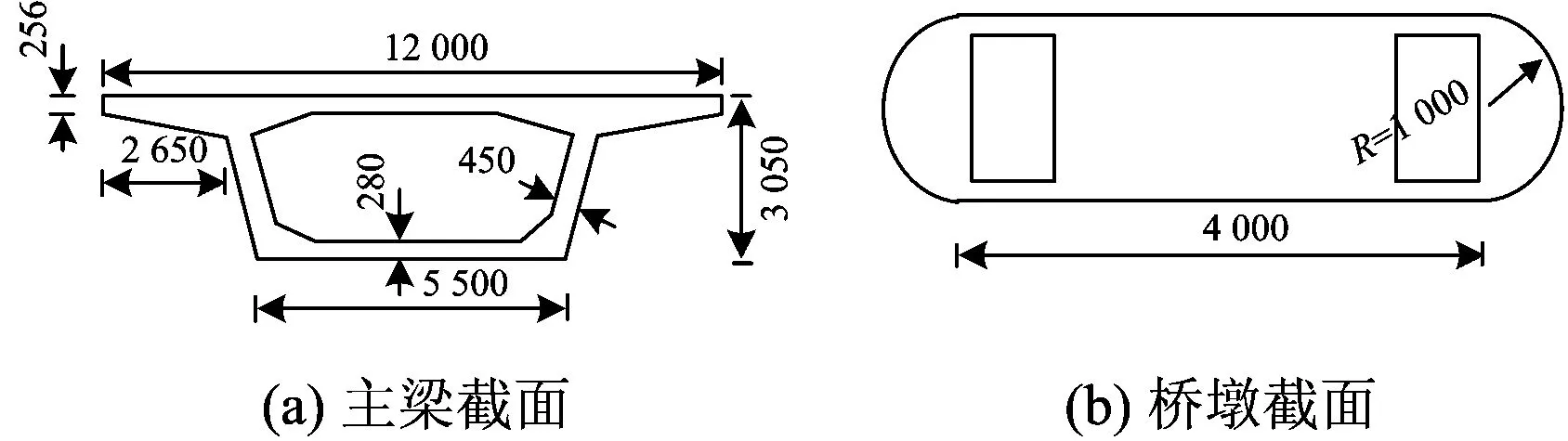
图6　桥梁截面示意图(单位：mm)

图7　轨道—桥梁模型(单位：m)

6.1　SIM和CTM计算结果对比

在利用SIM计算系统动力响应时，通过多次试算可知，若时间积分步长大于等于0.2 ms，则会导致计算结果发散或严重失真。这与5.2节中基于简化模型所算得的SIM对于时间积分步长的要求相符合，表明5.2节中关于时间积分步长预判对于分离迭代法的时间积分步长选择具有一定的指导作用。为对比计算收敛条件下2种方法计算结果的精度，在Δt=0.1 ms的时间积分积分步长下，利用2种方法计算了系统的动力响应，计算结果见表1及图8、图9和图10。可以看出，2种方法计算所得的桥梁跨中加速度、垂向轮轨力及车体加速度等动力响应的最大误差仅为2.5%，说明在足够小的时间积分步长条件下，2种方法均可以得到理想的耦合系统动力响应结果。

表1　2种方法计算响应最大值对比

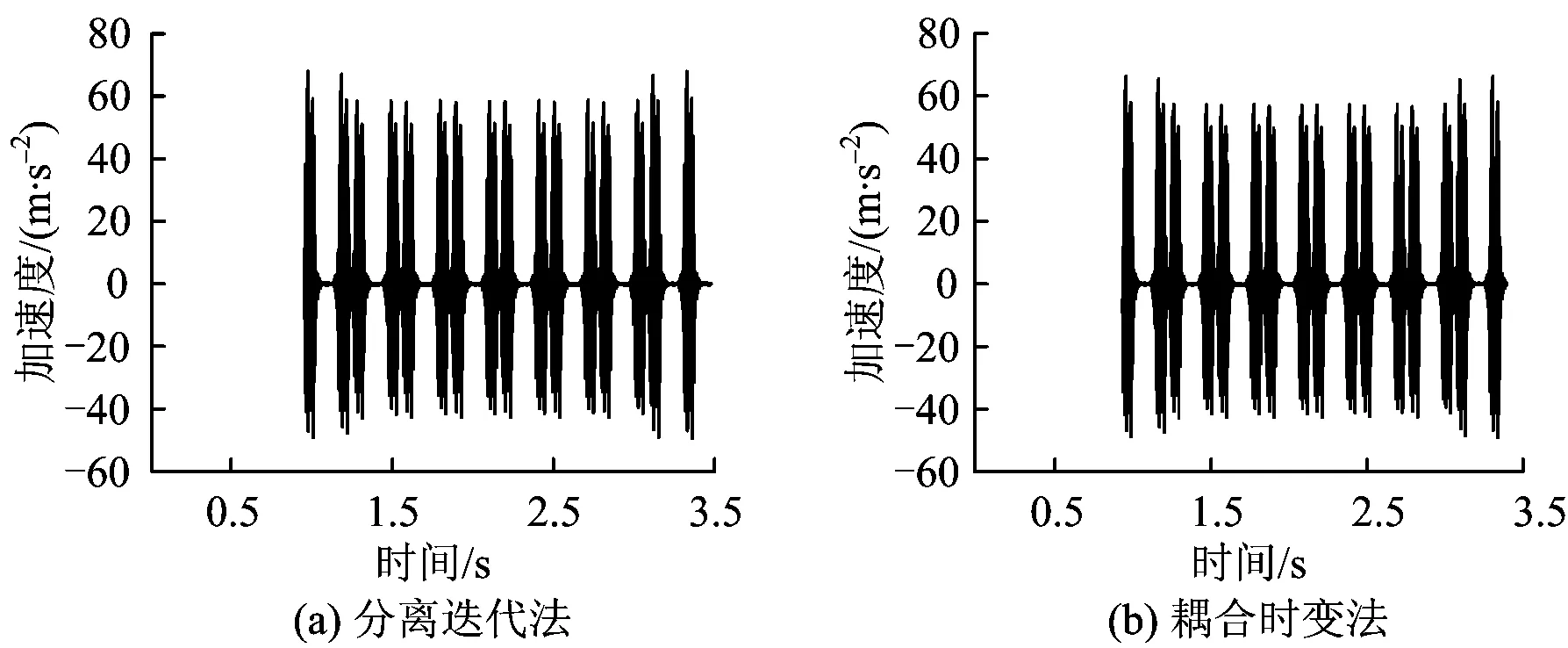
图8　2种方法A点竖向加速度对比

图9　2种方法A点竖向位移对比

图10　2种方法首轮对垂向轮轨力对比

6.2　不同动力响应指标的时间积分步长敏感性分析

在开展车—桥耦合系统动力响应分析时，CTM由于不存在迭代计算，单纯从动力方程计算稳定性来说，完全可以采用较SIM更大的时间积分步长。但由于车—桥耦合系统属于刚柔结合的动力系统，不同部位的动力响应计算精度受时间积分步长的影响各不相同；而且在实际研究中，并非所有动力响应指标都是关注对象。因此，研究不同动力响应指标计算精度对时间积分步长的敏感性有助于在保证计算精度的情况下确定合理的时间积分步长，提升计算效率。

图11—图16给出了利用耦合时变算法、时间积分步长在1～0.1 ms时耦合系统不同动力响应的最大值及其与0.1 ms时间积分步长时的相对误差。

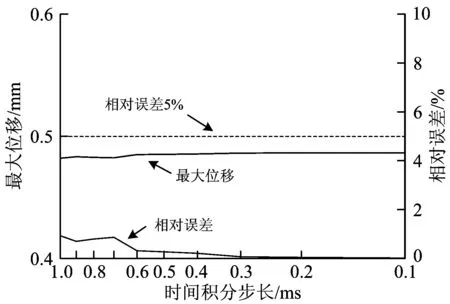
图11　A点最大位移及其相对误差

图12　A点最大加速度及其相对误差

从图11—图16可以看出：车辆、轨道—桥梁子系统的动力响应指标最大值均随着时间积分步长的减小逐渐趋近与稳定。其中，钢轨位移、车体加速度、桥梁位移、轮轨垂向力受时间积分步长的影响很小，即使是1 ms的时间积分步长，其相对误差百分比也不超过2%；桥梁加速度在时间积分步长为0.9 ms 时可得到相对误差小于5%的计算结果；钢轨加速度受时间积分步长影响最大，当时间积分步长为0.4 ms 时计算结果趋于稳定，主要原因在于钢轨振动频率比较高，较大的时间积分步长不足以准确捕捉钢轨加速度的峰值点。

图13　车体最大加速度及其相对误差

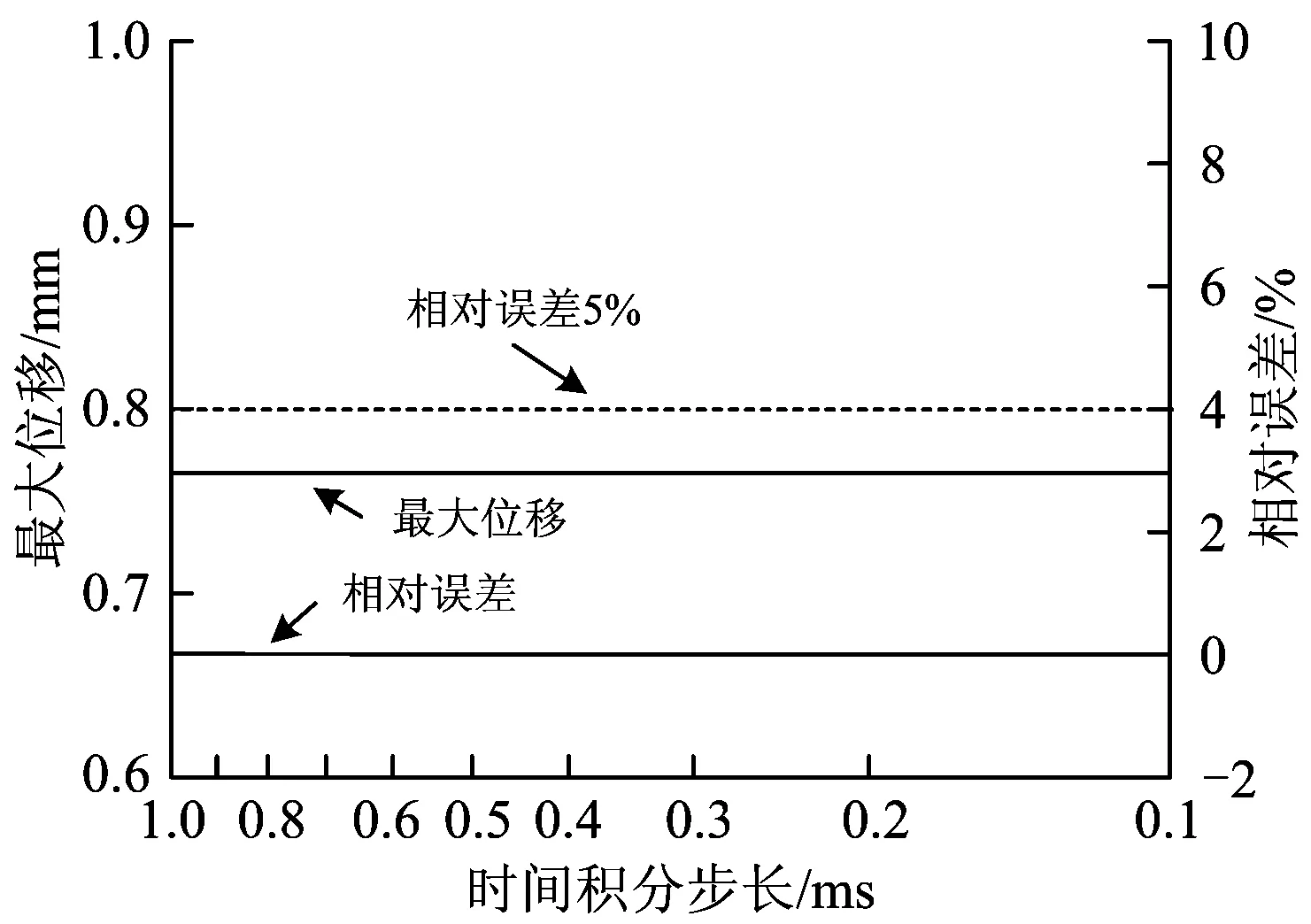
图14　B点最大位移及其相对误差

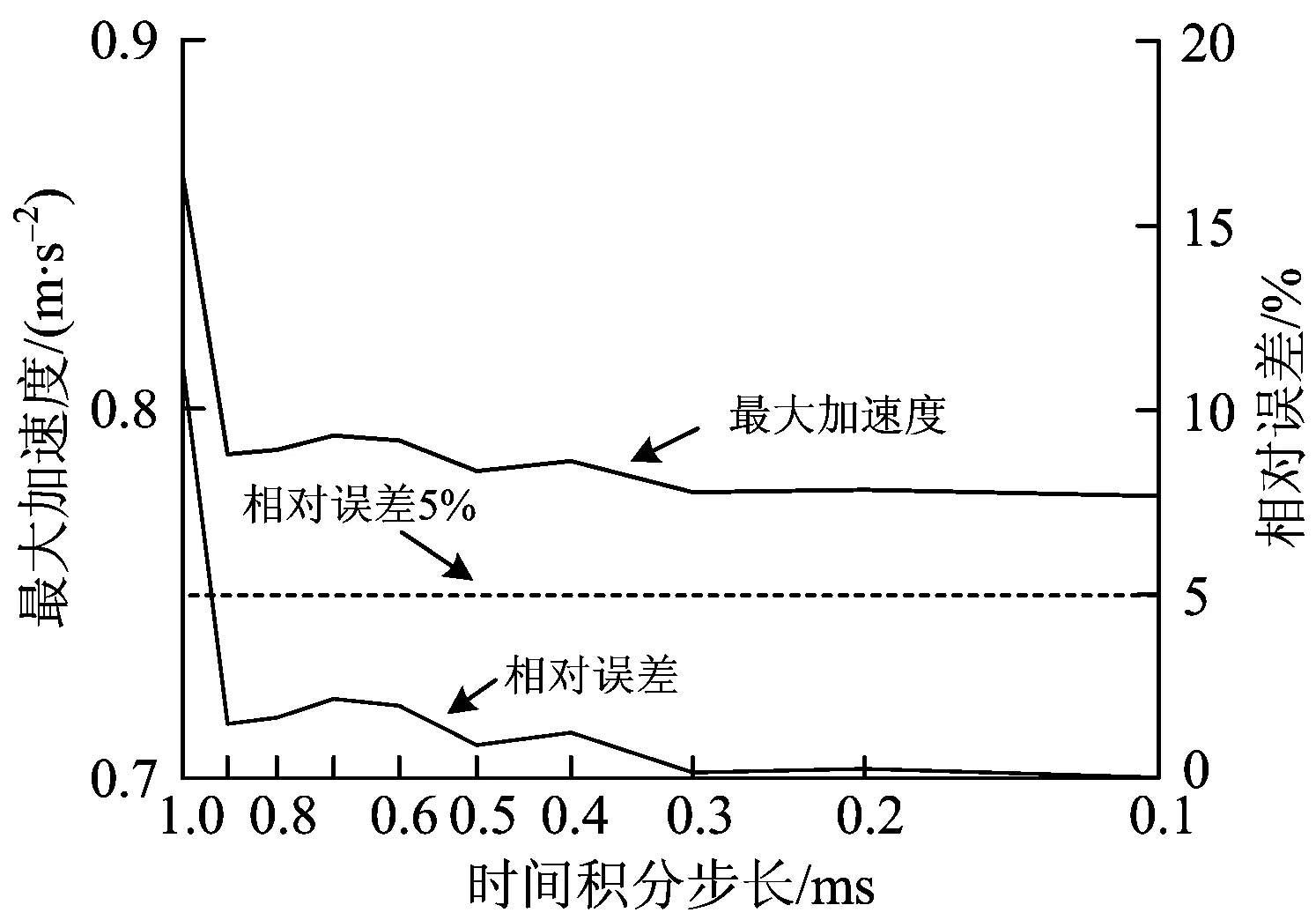
图15　B点最大加速度及其相对误差

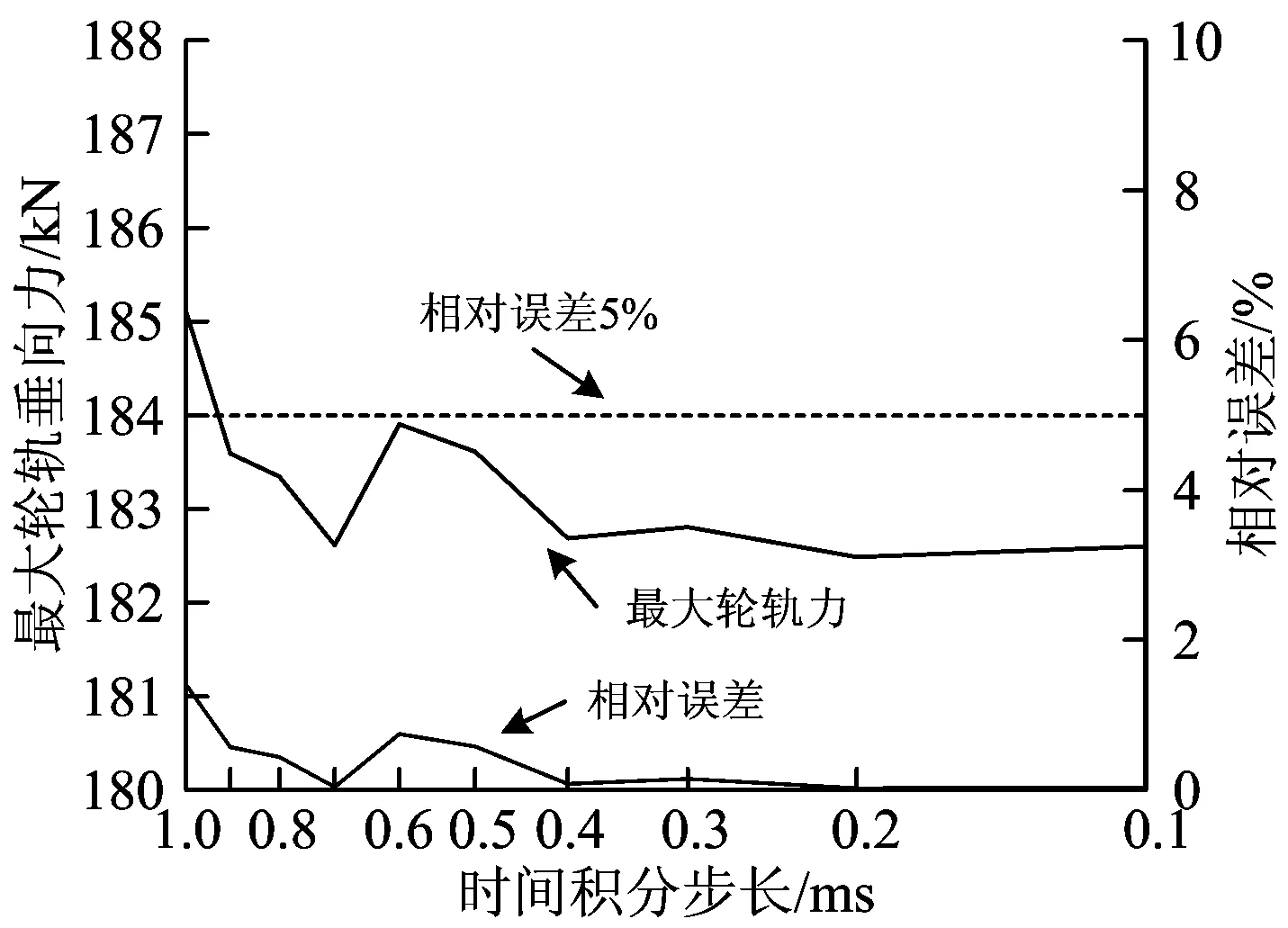
图16　最大轮轨垂向力及其相对误差

如果以5%的相对误差作为可接受的误差，则各项动力响应指标可接受的最大时间积分步长见表2。从表2可知，在相同时间积分步长情况下，CTM由于在每一时间步需要根据车轮位置重新形成系统刚度矩阵，从而导致计算时间比SIM长；但由于CTM采用直接积分法，避免了迭代收敛问题，故可以采用0.4 ms 的时间积分步长，使得CTM仍有计算效率上的优势。如果仅研究主梁冲击系数、乘坐舒适度指标，则利用CTM可采用1 ms的大时间步长，使计算效率提高5倍以上。

表2　2种方法计算时间及计算精度对比

7　结　论

(1)通过最大频率和谱半径理论可对动力响应计算的时间积分步长做初步的预测，SIM的时间积分步长受谱半径和系统最大频率2个指标控制，而CTM的时间积分步长主要由计算结果的准确性控制。

(2)在保证收敛的条件下，SIM和CTM均可以得到一致的耦合系统动力响应结果，SIM受时间积分步内迭代稳定性的影响，对时间积分步长有着较高要求，在本文算例中时间积分步长小于等于0.4 ms时才可得到收敛的计算结果；CTM则允许在较长的时间积分步长下进行动力响应计算。

(3)不同的动力响应指标计算精度对时间积分步长的敏感性不同，钢轨振动加速度最敏感；钢轨位移、车体加速度、桥梁位移、轮轨垂向力受时间积分步长的影响很小，如研究内容只与上述指标有关，则可利用CTM，采用1 ms的时间积分步长，以提高计算效率。

[1]CHEN Z, CHEN B. Recent Research and Applications of Numerical Simulation for Dynamic Response of Long-Span Bridges Subjected to Multiple Loads [J]. The Scientific World Journal, 2014(1):57-78.

[2]HU Nan, DAI Gonglian, YAN Bin, et al. Recent Development of Design and Construction of Medium and Long Span High-Speed Railway Bridges in China[J]. Engineering Structures, 2014, 74:233-241.

[3]翟婉明,夏禾.列车—轨道—桥梁动力相互作用理论与工程应用[M].北京:科学出版社,2011:212-213.

(ZHAI Wanming, XIA He. Train-Track-Bridge Dynamic Interaction: Theory and Engineering Application[M]. Beijing: Science Press, 2011:212-213. in Chinese)

[4]DOMÉNECH A, MUSEROS P, MARTíNEZ-RODRIGO M D. Influence of the Vehicle Model on the Prediction of the Maximum Bending Response of Simply-Supported Bridges under High-Speed Railway Traffic[J]. Engineering Structures, 2014,72:123-139.

[5]PABLO Antolin, ZHANG Nan, JOSE M Goicolea, et al. Consideration of Nonlinear Wheel-Rail Contact Forces for Dynamic Vehicle-Bridge Interaction in High-Speed Railways [J]. Journal of Sound and Vibration, 2013,332(5):1231-1251.

[6]LOU P, YU Z W, AU F T K. Rail-Bridge Coupling Element of Unequal Lengths for Analysing Train-Track-Bridge Interaction Systems[J]. Applied Mathematical Modelling, 2012, 36(4):1395-1414.

[7]LOU P. Finite Element Analysis for Train-Track-Bridge Interaction System[J]. Archive of Applied Mechanics, 2007, 77(10):707-728.

[8]崔圣爱,单德山,祝兵.南广高速铁路郁江大桥车桥耦合振动仿真分析[J]. 西南交通大学学报,2011, 46(3):385-390.

(CUI Shengai, SHAN Deshan, ZHU Bing. Simulation of Vehicle-Bridge Coupling Vibration for Yujiang River Bridge on Nanning-Guangzhou High-Speed Railway [J]. Journal of Southwest Jiaotong University, 2011, 46(3):385-390. in Chinese)

[9]王少钦，夏禾，郭薇薇，等. 风荷载—列车—大跨度桥梁系统非线性耦合振动分析[J].北京交通大学学报，2012，36(3):36-40.

(WANG Shaoqin, XIA He, GUO Weiwei, et al. Nonlinear Coupling Vibration Analysis of Wind Load-Train-Long-Span Bridge System[J]. Journal of Beijing Jiaotong University, 2012，36(3):36-40. in Chinese)

[10]朱志辉, 朱玉龙, 余志武，等. 96 m钢箱系杆拱桥动力响应及行车安全性分析[J]. 中国铁道科学, 2013, 34(6):21-29.

(ZHU Zhihui, ZHU Yulong, YU Zhiwu, et al. Analysis on the Dynamic Response and Running Safety of 96 m Steel Box Tied Arch Bridge[J]. China Railway Science, 2013,34(6):21-29. in Chinese)

[11]杜宪亭, 夏禾, 张田, 等. 基于精细Runge-Kutta混合积分法的车桥耦合振动非迭代求解算法[J]. 振动与冲击,2013,32(13):39-42,55.

(DU Xianting, XIA He, ZHANG Tian, et al. Non-Iterative Solving Algorithm for Coupled Vibration of a Train-Bridge System Based on Precise Runge-Kutta Hybrid Integration Method[J]. Journal of Vibration and Shock,2013,32(13): 39-42,55. in Chinese)

[12]吴定俊, 李奇, 陈艾荣. 车桥耦合振动迭代求解数值稳定性问题[J].力学季刊,2007,28(3):405-411.

(WU Dingjun, LI Qi, CHEN Airong. Numerical Stability of Iteration Scheme for Solution of Vehicle-Bridge Coupling Vibration[J]. Chinese Quarterly of Mechanics, 2007, 28(3): 405-411. in Chinese)

[13]GUO W H, XU Y L. Fully Computerized Approach to Study Cable-Stayed Bridge-Vehicle Interaction[J]. Journal of Sound and Vibration, 2001, 248(4):745-761.

[14]WANG W, YAN W, DENG L, et al. Dynamic Analysis of a Cable-Stayed Concrete-Filled Steel Tube Arch Bridge under Vehicle Loading[J]. Journal of Bridge Engineering, 2015,20(5)10.1061/(ASCE)BE.1943-5592.0000675，04014082.

[15]DENG L, CAI C S. Development of Dynamic Impact Factor for Performance Evaluation of Existing Multi-Girder Concrete Bridges[J]. Engineering Structures, 2010, 32(1):21-31.

[16]GU G. Resonance in Long-Span Railway Bridges Carrying TGV Trains[J]. Computers & Structures, 2015, (152): 185-199.

[17]杜宪亭，夏禾，张田. 车桥耦合振动迭代求解稳定性研究[J]. 振动与冲击，2012，31(22):62-65.

(DU Xianting, XIA He, ZHANG Tian. Numerical Stability of Iterative Scheme in Solving Coupled Vibration of a Train-Bridge System[J]. Journal of Vibration and Shock, 2012，31(22):62-65. in Chinese)

[18]ZHANG N, XIA H. Dynamic Analysis of Coupled Vehicle-Bridge System Based on Inter-System Iteration Method[J]. Computers & Structures, 2013(114/115): 26-34.

[19]郭文华, 陈代海, 李整. 二期恒载对大跨度斜拉桥车桥耦合振动的影响[J]. 中南大学学报: 自然科学版, 2011, 42(8): 2423-2429.

(GOU Wenhua, CHEN Daihai, LI Zheng. Influence of Secondary Dead Load on Vehicle-Bridge Coupling Vibration of Long-Span Cable-Stayed Bridges[J]. Journal of Central South University:Science and Technology,2011,42(8):2423-2429. in Chinese)

[20]张攀, 周昌盛, 王平. 轨下垫板刚度的时变特性及其影响研究[J]. 铁道标准设计, 2015, 59(9): 49-52.

(ZHANG Pan, ZHOU Changsheng, WANG Ping. Study on Time Variant Characteristics and Effects of Rail Pad Stiffness[J]. Railway Standard Design,2015,59(9):49-52. in Chinese)

[21]YANG Hongyin, CHEN Zhijun,LI Shaofan, et al. An Integrated Coupling Element for Vehicle-Rail-Bridge Integration System with a Non-Uniform Continuous Bridge [J]. Acta Mechanica Solida Sinica, 2015,28(3):313-330.

[22]张楠, 夏禾. 基于全过程迭代的车桥耦合动力系统分析方法[J]. 中国铁道科学, 2013, 34(5): 32-38.

(ZHANG Nan, XIA He. A Vehicle-Bridge Interaction Dynamic System Analysis Method Based on Inter-System Iteration[J]. China Railway Science,2013,34(5):32-38. in Chinese)

[23]夏禾,张楠,郭薇薇,等.车桥耦合振动工程[M].北京:科学出版社,2014.

(XIA He, ZHANG Nan, GUO Weiwei, et al. Coupling Vibration of Train-Bridge System[M]. Beijing: Science Press,2014. in Chinese)

[24]CLOUGH R W, PENZIEN J. Dynamics of Structures, Berkeley: Computers & Structures[M].New York:McGraw-Hill, 1993.

[25]程潜. 考虑列车纵向作用的高架车站动力分析[D].北京：北京交通大学,2013.

(CHENG Qian. Dynamic Analysis of Elevated Station Considering Vehicle Longitudinal Effects[D]. Beijing:Beijing Jiaotong University，2013.in Chinese)