铁路网检衡车组作业站点序列优化模型及算法
2016-04-10马树峰安爱民李学宝
马树峰,安爱民,王 龙,李学宝,王 颖
(1.中国铁道科学研究院 标准计量研究所,北京 100081;2.中国铁路经济规划研究院 运输研究所,北京 100038)
轨道衡和超偏载检测装置作为重要的铁路货运计量安全检测设备,在保证铁路运输安全、提高运输效率和质量等方面发挥了重要作用。检衡车是检定轨道衡和超偏载检测装置的计量标准器,是保证轨道衡和超偏载检测装置量值传递准确和统一的基础。根据相关规定,检衡车组(由5辆不同重量的检衡车固定编组而成)每年须在安装轨道衡和超偏载检测装置的车站(简称作业站点)进行1次检定作业。
近10年来,随着铁路对货运计量安全检测设备投资建设力度的加大,全路轨道衡的数量增长了50%,超偏载检测装置的数量增长了4倍,而检衡车组却一直未增加,导致检衡车组的运用非常紧张。因此,合理安排检衡车组在铁路网中进行检定作业的路径,即优化检衡车组经由各作业站点进行轨道衡、超偏载检测装置检定的作业次序(简称检衡车组作业站点序列),对于缩短检衡车组进行检定作业的时间、提高检衡车组的运用效率具有重要现实意义。由于文献[1—5]仅研究了检衡车组在站内检定工作的步骤和流程,因此笔者基于运筹学旅行商问题的建模思想,进行检衡车组作业站点序列优化的研究。
1 单组检衡车作业站点序列优化模型
受检衡车组数量的制约,在人工编制检衡车组运用计划时,通常根据拥有的检衡车组数量将全国路网划分为等量区域路网,并预先为每个区域路网分配1组检衡车。在执行具体检定任务时,每个区域路网又被分成若干个子区域路网,且检衡车组进入和离开子区域路网的起止站点一般是固定的,因此为实现单组检衡车在子区域路网内的广义走行时间最小化和检衡车组运用效率的最大化,可以将检衡车组作业站点序列的优化问题等价为运筹学中的旅行商问题(TSP),并基于TSP的建模原理构造子区域路网内检衡车组作业站点序列优化的模型。
以1组检衡车在所负责子区域路网内的广义走行时间最小为目标,建立的单组检衡车作业站点序列优化模型M1为
(1)
s.t.
(2)
(3)
(4)
(5)
ui-uj+nxij≤n-1i≠j≠s,i≠e
(6)
xij∈{0,1}
(7)
式中:N为某子区域路网内检衡车组作业站点的集合;s为所配属检衡车组进入该子区域路网内进行检定作业的第1个作业站点,s∈N;e为所配属检衡车组在该子区域路网内进行检定作业的最后1个作业站点,即检衡车组要离开该子区域路网时所在的作业站点,e∈N;xij和ui为0—1决策变量,i和j为子区域路网内的两相邻作业站点且i,j∈N;tij为检衡车组自作业站点i至j的广义走行时间,由于检衡车组在作业站点i完成检定作业之后需要连挂特定车次的货物列车前往作业站点j,因此,可能会在作业站点i以及途经各站产生一定的等待时间,故tij不仅包括检衡车组自i站至j站的运行时间,还包括在i站及沿途各站的等待时间,d;n为子区域路网内检衡车组作业站点的数量。
作为式(1)的约束条件,式(2)表示检衡车组在子区域路网内去往除s以外的其他作业站点时只能由1个作业站点出发;式(3)表示检衡车组在子区域路网内从除e以外的其他作业站点出发后只能到达1个作业站点;式(4)表示对于s站,检衡车组在子区域路网内只能从该站出发而不能到达该站;式(5)表示对于e站,检衡车组在子区域路网内只能到达该站而不能从该站出发;式(6)为检衡车组走行径路不构成回路的约束条件;式(7)表示当检衡车组在作业站点i完成检定作业后的下一个作业站点为j时,xij取1,否则取0。
2 单组检衡车作业站点序列优化模型的求解算法
作者采用收敛速度快、计算精度高的粒子群算法[6-8]对模型M1进行求解。该算法采用速度—位置搜索模式,以每个粒子的位置作为待解决问题的可能解集,以目标函数作为适应值来判断群体中每个粒子的优劣;通过跟踪个体最优值和全局最优值(即全部粒子个体极值的最优者)的粒子,不断更新其在解空间的位置,从而找到问题的最优解。
更新粒子速度和位置的传统表达式为
(8)
(9)

因为式(8)和式(9)为连续问题的求解式,在用于求解离散的TSP问题时,需要对其进化算子进行重新定义如下。
(1)位置:定义任意粒子的位置X代表检衡车组遍历子区域路网内作业站点的次序,即根据模型M1中决策变量xij的值推算出的检衡车组在子区域路网内进行检定作业时到达作业站点的次序。
(2)速度:定义任意粒子的速度V为粒子位置的交换集,它是由1组交换构成置换序列的有序列表,其表达形式为
V={(i,j)h|h=1,2,…,P}
式中:P表示该速度所含交换的数目,交换按顺序依次执行。
(3)位置与速度相加:将1组置换序列依次作用于某个粒子的位置,生成1个新的位置;例如,位置X1=(1,3,2,5,4,6)表示检衡车组的作业站点序列为1→3→2→5→4→6(数字为作业站点的编号),相当于在模型M1中,n=6且x13=1,x32=1,x25=1,x54=1和x46=1,其余决策变量值均为0;速度V1={(5,2),(3,2)}表示先进行检衡车组第5与第2序位作业站点的交换,再进行第3第与2序位作业站点的交换,则X1+V1=(1,2,4,5,3,6),相当于经过位置与速度的加和后,决策变量的值变更为:x12=1,x24=1,x45=1,x53=1和x36=1,其余决策变量值均为0,检衡车组的作业站点序列调整为1→2→4→5→3→6。
(4)位置与位置相减:该操作的结果是得到1组置换序列,即速度;例如,位置X1=(1,3,2,5,4,6),位置X2=(1,2,4,5,3,6),则X2-X1={(5,2),(3,2)}。
(5)速度与速度相加:对2个置换序列进行合并,可得到1个新的置换序列(即1个新的速度)作为指导检衡车组的作业站点序列优化调整的原则。例如,速度V1={(5,2),(3,2)},速度V2={(1,4)},则V1+V2={(5,2),(3,2),(1,4)}。
(6)实数与速度相乘:设实数r为(0,1)区间内的随机数,速度V为包含P个交换的序列,则r与V相乘的结果为由V中前r×P(取整)个交换构成1组新的置换序列。例如,V={(1,3),(2,5),(4,1),(3,2)},则当r=0.6时,r×V={(1,3),(2,5)}。
由此,针对用模型M1求解离散TSP问题,对式(8)和式(9)进行变换,得
(10)
(11)
式中:α和β为加速常数,一般在(0,1)区间内取值,α和β决定了后面的交换被用到几个,α和β即为r×P下的取整。
基于粒子群算法的模型M1求解步骤如下。
Step 1:先设定粒子的数量(本文取30),每个粒子代表1个解,即检衡车组作业站点序列的1个方案;Lmax为最大迭代次数(可取为1 000)。
Step 2:随机生成每个粒子的初始位置和初始速度,计迭代次数l=1。
Step 3:根据式(10)和式(11)对所有粒子的位置进行更新,并用式(1)计算每个粒子的适应值,即所对应检衡车组作业站点序列方案下检衡车组在各站点间的广义走行时间。
Step 4:判断每个粒子的适应值是否优于其自身已经历过的个体极值,若是,更新其个体极值(即用该粒子当前的适应值替换其个体极值),否则,其个体极值不变。
Step 5:判断每个粒子的个体极值是否优于当前的全局极值,若是,更新全局极值,否则全局极值不变。l=l+1。
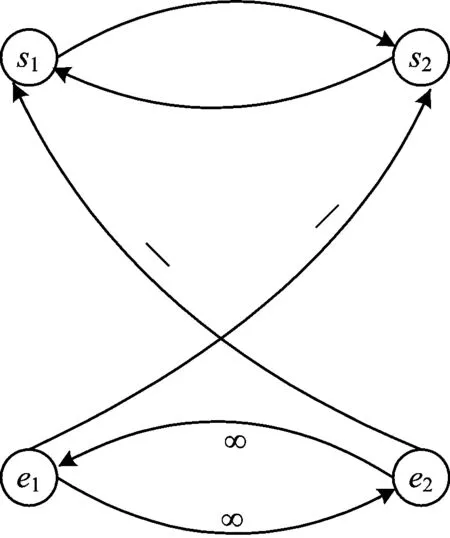
Step 6:判断是否满足l Step 7:结束寻优操作,输出计算结果。 前文研究了由1组检衡车担任1个子区域路网内各相关作业站点检定任务时的作业站点序列优化问题。考虑到今后将增配检衡车组,每个区域路网有可能配备多组检衡车进行检定作业的情况,并且从全局优化的角度分析,由于依照人工经验所划分的子区域路网并不能保证多组检衡车分别对所负责子区域路网内各作业站点进行检定作业而消耗的总的广义走行时间最少,以及各组检衡车的工作负荷基本均衡等要求,因此,作者再从全局优化的角度出发,将某一区域路网视为一个整体,打破以往1组检衡车独立负责一个区域的“分片负责”的固定检定范围模式,在锁定各组检衡车进入和离开所负责检定区域路网内作业站点的情况下,研究多组检衡车联合开展某一区域路网作业站点检定作业时检衡车组作业站点序列综合优化的问题。 通过分析可知,多组检衡车在某区域路网内进行检定作业时的作业站点序列优化问题可类比为多个旅行商的走行径路优化问题(即MTSP问题)。 基于MTSP问题的建模思想,可构建多组检衡车作业站点序列优化模型M2为 (12) s.t. (13) (14) (15) (16) (17) (18) 式(12)为模型M2的目标函数,表示配属给某铁路局的多组检衡车在该铁路局管内路网范围内总的广义走行时间最小;式(13)表示检衡车组k在该铁路局管内路网范围内去往除sk以外的其他作业站点时只能由1个作业站点出发;式(14)表示检衡车组k在该铁路局管内路网范围内从除ek以外的其他作业站点出发后只能到达1个作业站点;式(15)表示检衡车组k只从sk站出发而不能到达该站;式(16)表示检衡车组只到达ek站而郴能从该站出发;式(17)中,Ω为消去支路的约束[8-9],即消去构成不完整径路的解,以避免在每次遍历当中产生多于1个的互不连通路径。 为了便于模型M2的求解,本文根据文献[9],通过设置虚拟弧费用(即检衡车组经由虚拟弧的广义走行时间),将求解模型M2的MTSP问题转换为TSP问题。下面以2组检衡车负责某一铁路局管内路网各作业站点的检定任务为例,给出虚拟弧的具体设置方法(见图1)如下。 (1)因为2组检衡车的起点作业站之间不能有连接弧相连,所以设连接它们起点作业站的连接弧的弧费用为无穷大。 (2)同理,由于在2组检衡车的终点作业站之间也不能有连接弧,因此设连接它们终点作业站的连接弧的弧费用也为无穷大。 (3)因为其中1组检衡车(假定该组检衡车的编号k为1)的终点作业站必须与另1组检衡车(假定该组检衡车的编号k为2)的起点作业站相连,所以设对应该连接弧的弧费用为负值。 由此,即可构建求解MTSP问题的虚拟路网结构,从而实现MTSP问题向TSP问题的转化;然后,调用本文给出的对进化算子重新定义的粒子群算法求解离散TSP问题,即可实现等价条件下MTSP问题的求解。 图1 2组检衡车情况下虚拟弧费用的设置 以哈尔滨铁路局管内路网的检衡车组作业站点序列优化为例,验证本文模型和算法的有效性。如图2所示,哈尔滨铁路局管内路网内共有89个车站点安装了轨道衡和超偏载检测装置,并假定配备了2组检衡车负责这些作业站点的轨道衡和超偏载装置的检定任务。 图2 哈尔滨铁路局管内路网作业站点布局图 在既有的检衡车组运用方案中,将哈尔滨铁路局管内路网划分为2个作业区,如图2中右侧虚线框内为检衡车组1的作业区,检衡车组1由温春站进入、从五常站离开自己的作业区;路网的其余部分为检衡车组2的作业区,检衡车组2从卧里屯站进入、从哈尔滨南站驶离自己的作业区。 按照既有检衡车组运用方案,基于模型M1,对检衡车组1的作业站点序列进行优化,所获得的检衡车组1的作业站点序列见表1。 表1对应的检衡车组1在其作业区内总的广义走行时间为80.5 d,而按检衡车组1的既有运用计划则需要93 d(如果考虑检衡车组的厂修、段修和周期检定所需要的时间,以此效率推算,每一检衡车组大概平均仅能完成其全年检定计划的80%);由此可知,采用本文的单组检衡车作业站点序列优化模型及求解算法可节省12.5d,即检衡车组1的运用效率提高了13.44%。 在检衡车组1由温春站进入、从五常站离开哈尔滨铁路局管内路网,以及检衡车组2从卧里屯站进入、从哈尔滨南站离开哈尔滨铁路局管内路网的前提条件下,按照求解MTSP问题的思路,打破既有检衡车组运用方案对检衡车组1和检衡车组2作业区的限制,基于模型M2对检衡车组1和检衡车组2的走行径路进行整体优化,所获得的这2组检衡车的作业站点序列分别见表2和表3。 由表2和表3得到的检衡车组1和检衡车组2在哈尔滨铁路局管内路网内共同进行检定作业所用的广义走行时间合计为120.5 d,而按检衡车组1和检衡车组2的既有运用计划则共计需要141 d;由此可知,采用本文的多组检衡车作业站点序列优化模型可节省20.5d的广义走行时间,检衡车组的整体运用效率提高了14.54%。此外,相对于预先固定每组检衡车的作业区的传统检衡车组运用方案,基于MTSP问题求解思路的模型M2对同一路网内多组检衡车的作业站点序列进行整体优化,不但能够使各组检衡车的作业负荷更具均衡性,而且总体上检衡车组的广义走行时间也更加节省。 表1 基于TSP问题求解的检衡车组1的作业站点序列 表2 基于MTSP问题求解的检衡车组1的作业站点序列 表3 基于MTSP问题求解的检衡车组2的作业站点序列 本文基于运筹学旅行商问题的求解思路,针对检衡车组作业站点序列优化问题,分别构建了单组和多组检衡车作业站点序列优化模型,设计了基于改进的粒子群算法对模型进行求解;并以哈尔滨铁路局管内路网的检衡车组作业站点序列优化为例,验证了模型和算法的有效性。 [1]马树峰,王颖.关于强化铁路货车超偏载检测装置运用管理工作的探讨[J].铁道运输与经济,2011,33(12):30-33. (MA Shufeng,WANG Ying.On Strengthening the Management of Railway Wagon Super Partial Load Detection Device Using Work[J]. Railway Transport and Economy,2011,33(12):30-33.in Chinese) [2]王颖.强化货运计量安全检测监控系统运用管理的思考[J].铁道运输与经济,2010,32(4):79-81. (WANG Ying.Thoughts on Strengthening Utilization Management for Measurement Safety Monitoring System for Freight Traffic[J]. Railway Transport and Economy,2010,32(4):79-81. in Chinese) [3]何小菊. 超偏载检测装置检定工作介绍[J].铁道技术监督,2009,37(8):23-24. (HE Xiaoju. Introduction of the Calibration Equipment of Overloading and Unbalanced Loading Detecting Device[J]. Railway Quality Control, 2009,37(8):23-24. in Chinese) [4]段小军.T7型检衡车使用、维护及检定情况概述[J].铁道技术监督,2007,35(10):42-43. (DUAN Xiaojun.General Introduction of the Utilization, Maintenance and Calibration of T7Type of Weight Bridge Test Car[J]. Railway Quality Control, 2007,35(10):42-43. in Chinese) [5]徐锋.动态检衡车运用专家系统初探[J].铁道技术监督,2006,34(9):33-34. (XU Feng. Exploration on Applying Expert System on Dynamic Weight Bridge Test Car[J]. Railway Quality Control, 2006,34(9):33-34. in Chinese) [6]马晓慧,王红. 改进的PSO在TSP中的应用[J].计算机与现代化,2011(9):5-7,11. (MA Xiaohui, WANG Hong. Application of Improved PSO in TSP[J]. Computer and Modernization, 2011(9):5-7,11. in Chinese) [7]钟一文,杨建刚,宁正元.求解TSP问题的离散粒子群优化算法[J].系统工程理论与实践,2006,16(6):88-94. (ZHONG Yiwen, YANG Jiangang, NING Zhengyuan. Discrete Particle Swarm Optimization Algorithm for TSP Problem[J]. System Engineering Theory & Practice, 2006,16(6):88-94. in Chinese) [8]高尚,韩斌,吴小俊,等.求解旅行商问题的混合粒子群优化算法[J].控制与决策,2004,19(11):1286-1289. (GAO Shang, HAN Bin, WU Xiaojun, et al. Solving Traveling Salesman Problem by Hybrid Particle Swarm Optimization Algorithm[J]. Control and Decision, 2004,19(11):1286-1289. in Chinese) [9]杨国兴.一种多出发点多旅行商问题到旅行商问题的转换[J].系统工程理论方法应用,1993,2(3):66-68. (YANG Guoxing. A Transformation of the Multi-Depot Multi-Salesmen Problem to the Standard Traveling Salesman Problem[J]. Systems Engineering Theory Methodology Applications, 1993,2(3):66-68. in Chinese)3 多组检衡车作业站点序列优化
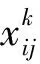
4 实例验证

4.1 单组检衡车作业站点序列的优化
4.2 多组检衡车作业站点序列的优化



5 结 语
