Beta-Binomial回归模型及其应用

赵为华，张日权

(1. 南通大学 理学院，江苏 南通226019； 2. 华东师范大学 金融与统计学院，上海200241)



Beta-Binomial回归模型及其应用

赵为华1，张日权2

(1. 南通大学 理学院，江苏 南通226019； 2. 华东师范大学 金融与统计学院，上海200241)

摘要：在成败型试验中或满意度支持率调查中，Beta-Binomial分布常被用来刻画具有偏大离差的计数型比例数据，由此提出Beta-Binomial 回归模型，研究参数的最大似然估计方法并基于Newton-Raphson算法给出参数估计的迭代方法；重点讨论模型中回归参数和相关性参数存在的检验问题，提出Score检验方法并通过数值模拟研究Score检验统计量的检验功效问题；实例分析证明Beta-Binomial 回归模型的有用性。

关键词：比例数据；Beta-Binomial 分布；偏大离差；相关性

一、引 言

在许多生物学和医学试验或某项政策的社会满意度调查中，常常得到的数据是计数型比例数据的形式，即Y/m，其中m是试验次数(调查的人数)，Y是试验中成功的次数(支持政策的人数)。当m固定时，随机变量Y可以看成是m个相互独立的Bernoulli随机变量的和，即Y=W1+W2…+Wm服从二项分布(binomialdistribution)，记为 b(m,p)。然而，在一些实际问题中 W1,W2,…,Wm之间的独立性并不能得到满足，例如在抽样调查中，当两个样本来自于同一个家庭或行业时，回答的结果就不再具有独立性，而往往存在相关性， Y=W1+W2+…+Wm就不再服从二项分布。此时，如果仍然基于二项分布预测试验成功率或政策支持率的话，会导致估计偏差较大、预测不准确等弱点。

E(Y)=mp

Var(Y)=mp(1-p)[1+(m-1)δ]

(1)

很明显当δ=0，式(1)退化成二项分布的方差，而当δ>0时可以用来刻画偏大离差计数数据，而当δ<0时可以用来刻画偏小离差计数数据(实际情况中很少发生)。

为刻画具有相关性Bernoulli随机变量和的分布，许多研究者提出使用混合分布(mixture)或复合分布来描述响应计数数据，其中最常用的方法是Beta-Binomial分布，即Y在给定参数p时服从二项分布 Y|p～b(m,p)，同时p服从beta分布，p～beta(a,b)，其中a>0和b>0为两个未知参数[1]。众所周知，beta分布是二项分布p的共轭先验分布，且Y的分布列为：

(y=1,2，…,m)

(2)

以及Beta-Binomial分布的期望和方差为：

E(Y)=ma(a+b)-1

Var(Y)=mab(a+b)-2[1+(m-1)(a+b+1)-1]

(3)

令θ=a/(a+b)-1，δ=(a+b+1)-1，由式(1)可知，Beta-Binomial分布可以用来刻画具有偏大离差的计数数据且Wj之间的相关性为δ=(a+b+1)-1。已有文献已对Beta-Binomial模型展开过一些研究，分别将之应用到生物学、生物化学和社会调查学等领域中[2-4]；申跃等基于经验Bayes估计方法将Beta-Binomial应用到商品售后抱怨率问题中[5]；Paulo主要介绍了如何使用Stata软件估计Beta-Binomial分布中的未知参数[6]；赵为华等则应用EM算法研究Beta-Binomial模型中未知参数的估计方法，并将之应用到学生考试不及格率和优秀率的估计问题[7]。

然而，已有文献主要研究Beta-Binomial模型及其应用问题，很少研究基于Beta-Binomial分布的回归建模及其统计推断问题。本文将基于Newton-Raphson算法研究Beta-Binomial回归模型的参数估计问题，并重点讨论回归参数和相关性参数的检验问题。

二、Beta-Binomial 回归模型及其参数估计

(4)

其中β=(β1,β2,…,βp)T是p维回归系数。 如果假定自变量中的第一个分量xi1≡1，则模型(4)中包含了常数项。

根据式(2)，在忽略与参数无关的常数后，Beta-Binomial回归模型的对数似然函数可表示为：

l(β,φ)=

(5)

其中φ=δ(1-δ)-1，当δ=0亦即φ=0时，Beta-

Binomial的对数似然退化成Binomial回归的对数似然。

由式(5)，得到参数β和φ的得分函数为：

(6)

进一步，可得观测Fisher信息阵为：

(7)

(i=1,2,…,n)

记η=(βT,φ)T。由式(6)和(7)，根据Newton-Raphson算法得到迭代公式为：

η(k+1)=η(k)+I-1S|η(k)

三、参数的Score检验

在实际回归建模时，需要评价模型的正确性和模型中自变量的重要性。为此下面应用Score检验统计量对相关性参数φ和回归系数β的重要性进行检验。Score检验统计量最大的优点是只需要在原假设成立情况下计算参数估计。

对于相关性参数φ，本文提出检验问题：

H01:φ=0↔H11:φ>0

(8)

(9)

其中Iφφ为观测Fisher信息阵的逆矩阵对应参数φ的分块。通过一些简单推导，检验统计量SC1渐近服从自由度为1的卡方分布χ2(1)。

H02:βb=0↔H12:βb≠0

(10)

(11)

四、数值模拟

下面通过随机模拟来说明估计方法的有效性以及检验统计量的检验功效。响应变量数据由如下模型随机产生：

yi|pi～b(mi,pi)，pi～beta(θiω,(1-θi)ω)

表1　不同样本量下参数β和φ的偏差、绝对值偏差及其标准差估计表

表1的结果表明，估计量的偏差都较小，且随着样本量n的增加估计的绝对值偏差越来越接近于0。此外，不同样本量下估计量的标准差估计和样本标准差估计非常接近，且都随着n的增大接近于0。图 1 显示了回归系数β和相关性参数φ=1/ω估计的均方误差(MSE)箱线图，易见随着样本量的增大，本文的估计效果是令人满意的。

下面研究Score检验统计量的检验功效问题。在数据生成时，其他参数保持不变的情况下，分别取β5=0，0.1，0.2，0.3，0.4，0.5和1时，考察检验统计量(11)的检验功效，即在显著性水平0.05下，计算1 000次模拟中拒绝原假设H0:β5=0的比例，结果见表2和图2。

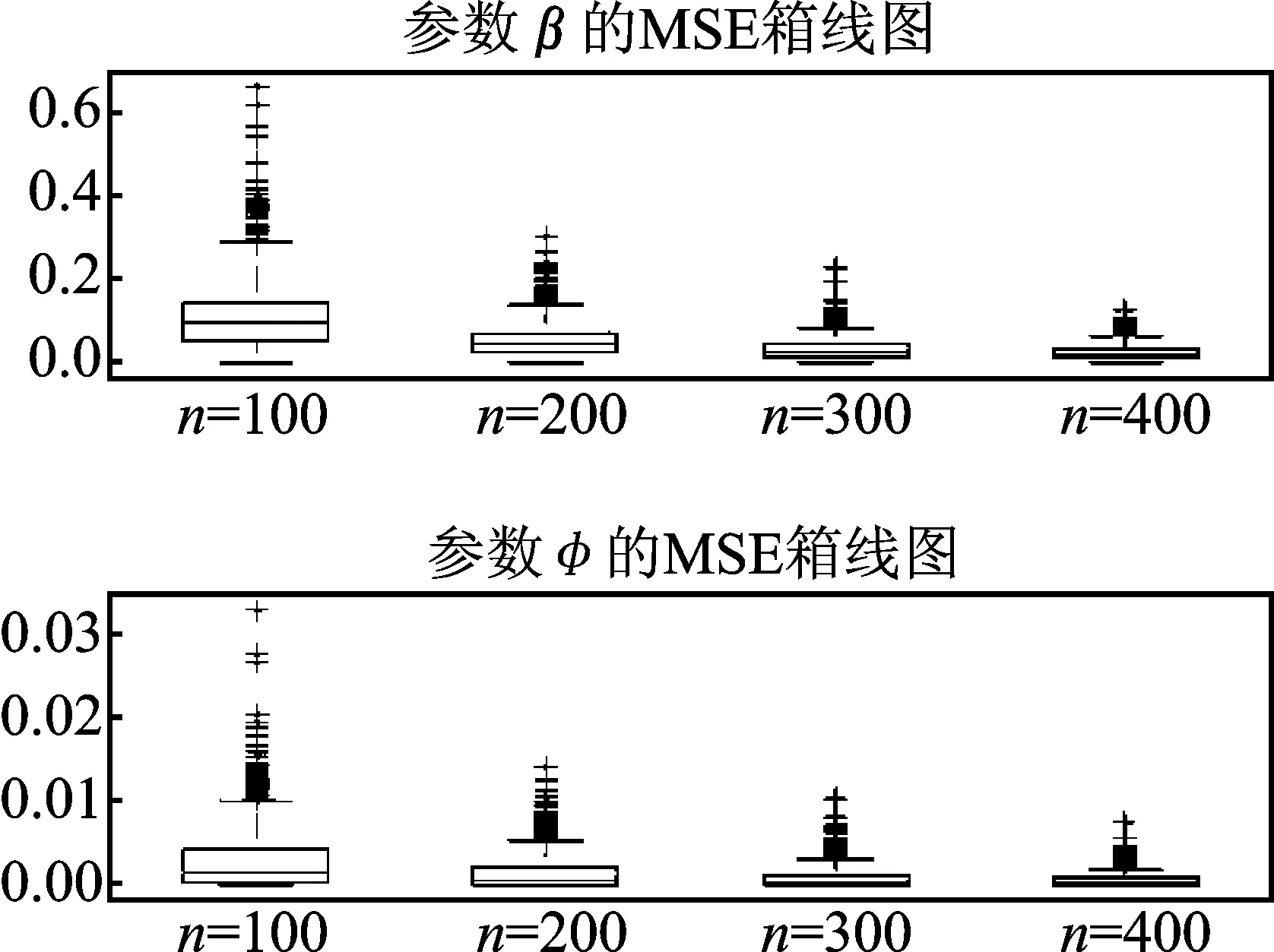
图1　参数估计MSE的箱线图

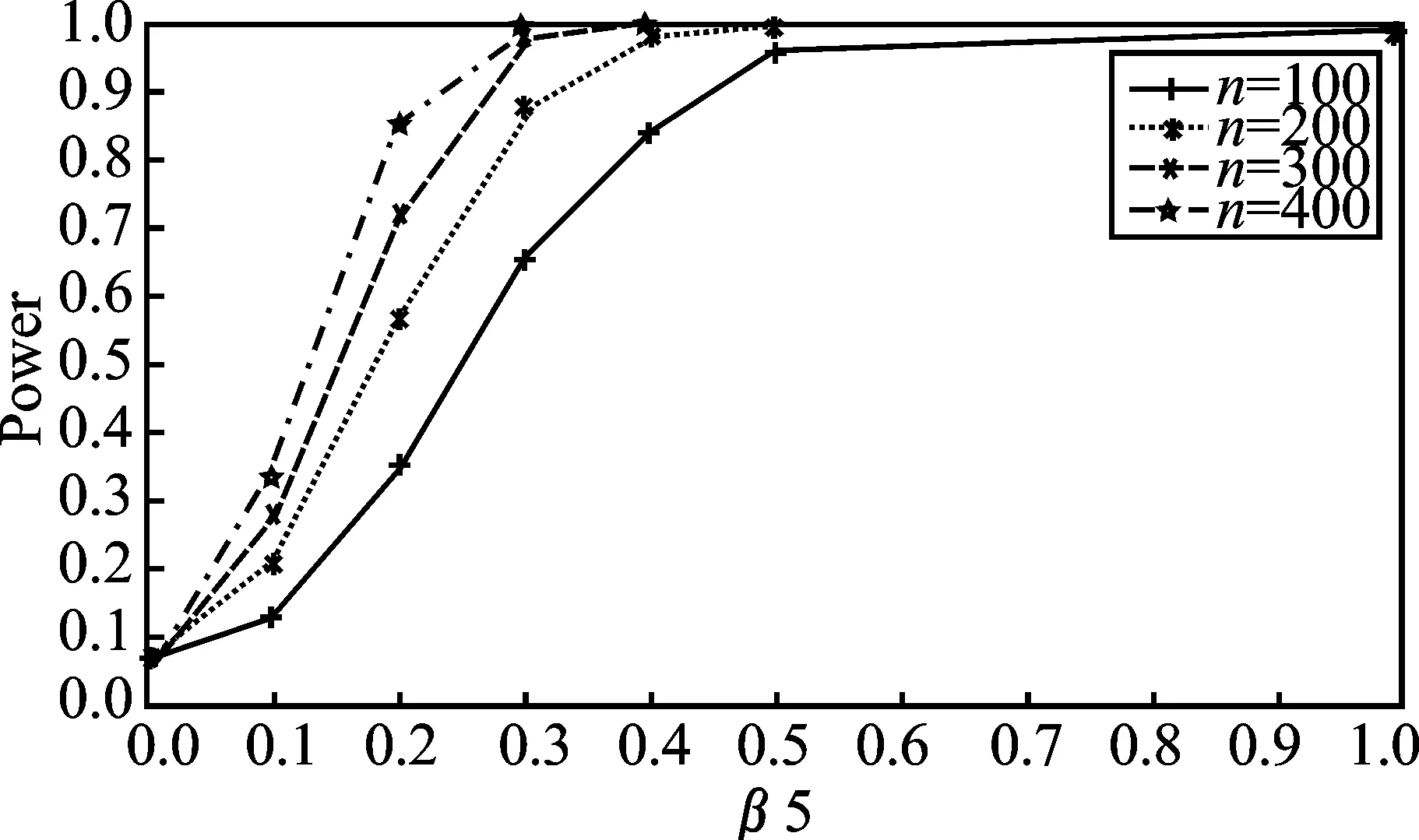
图2　参数β5的检验功效图

从表2和图2易见，在相同的样本量下，随着参数β5的取值远离0，检验的功效显著增加；另外一方面，随着样本量的增大，检验的功效迅速接近于1，且在原假设正确时(β5=0)，检验的功效非常接近于名义水平0.05。

相关性参数φ的检验功效见表3和图3，其中模拟中ω分别取1 000，500，100，50，20，10，5，3，对应的相关性φ=1/1 000，1/500，1/250,1/100，1/50，1/20，1/10，1/3由弱到强(φ=1/1 000可近似地认为不相关)。模拟结果再次表明：参数接近于原假设时，检验的功效与名义水平非常接近，当远离原假设时，检验的功效随着样本量的增大迅速提高。

表2　不同样本量下β5的检验功效表

表3　不同样本量下φ的检验功效表

图3　参数φ的检验功效图

五、实例分析

Wheatley等研究和报道了欧洲胡萝卜蝇对植物胡萝卜生长的破坏数据[8]。该数据共有36 组数据，主要是用来研究喷洒农药的剂量( 共5 种不同剂量)和喷洒杀虫剂农药的类型(即二嗪农杀虫剂(diazinon)、乙拌磷杀虫剂(disulfoton)以及不喷洒农药)对控制胡萝卜蝇破坏胡萝卜植物生长是否有显著影响。以mi表示进入研究的植物数目，yi表示受到破坏的植物数目，xi1表示喷洒农药的剂量，xi2和xi3表示0-1型分类变量，即：

(i=1,2，…,36)

由于该数据存在明显的偏大离差，Hardin等提出了具有偏大离差的计数回归模型拟合该数据[9]160-161。这里，使本文提出的Beta-Binomial回归模型(4)再次分析该数据，其结果见表4(为比较起见，表中亦包含Binomial回归模型拟合结果)。

表4　欧洲胡萝卜蝇数据的拟合结果表

从表4 不难看出，喷洒杀虫剂的种类以及是否喷洒农药有显著差异，且系数β1和β2的估计是负值，说明喷洒对有效防治胡萝卜蝇的破坏性有着重要作用；另外一方面，系数β3的检验p值在两个模型下均大于0.05，说明增加喷洒剂量对防治胡萝卜蝇破坏作用不敏感。同时，模型的拟合优度BIC值清晰地表明Beta-Binomial模型好于Binomial回归模型。

为进一步检验Beta-Binomial模型的有用性，我们计算Score检验统计量(9)，其结果为：

SC1=224.794 0>>χ2(1)=3.841 5

再次清楚地说明数据中存在着偏大离差，此时直接使用Binomial模型拟合数据会导致拟合不充分、推断效果较差等问题。

六、总结

Beta-Binomial分布是一种混合分布模型，能够处理具有偏大离差的计数型比例数据。本文基于Beta-Binomial分布提出了Beta-Binomial回归模型，给出了模型中参数的最大似然估计方法，并基于Score经验统计量给出了重要变量和相关性参数的检验问题。数值模拟和实例分析充分说明了所提方法的有效性。进一步，为刻画数据的相关性和异质性，提高估计和预测的准确性，在Beta-Binomial模型中可以对均值参数和相关性参数进行同时回归建模，并研究回归系数的重要性检验问题以及对模型进行拟合优度检验。

参考文献：

[1]Crowder M. Beta-Binomial ANOVA for Proportions[J]. Applied Statistics, 1978, 27.

[2]Otake M, Prenticce R. The Analysis of Chromosomally Aberrant Cells Based on a Beta-Binomial Distribution[J]. Radiation Research, 1984, 98(3).

[3]Prentice R. Binary Regression Using an Extended Beta-Binomial Distribution, with Discussion of Correlation Induced by Covariate Measurement Errors[J]. Journal of the American Statistical Association, 1986, 81(394).

[4]Silverman B, Wilson J. A Beta-Binomial Model for Library Survey Data[J]. Journal of Documentation, 1987, 43(2).

[5]申跃, 赵平. Beta-Binomial 模型和经验贝叶斯方法在抱怨行为倾向性研究中的应用[J]. 统计研究, 2004, 21( 11).

[6]Paulo, Guimaraes. A Simple Approach to Fit the Beta-Binomial Model[J]. Stata Journal, 2005, 5(3).

[7]赵为华, 李泽安, 陆志峰. Beta-Binomial 模型基于EM 算法的应用研究[J]. 大学数学, 2010, 26(3).

[8]Wheatley G, Freeman, G. A Method of Using the Proportion of Undamaged Carrots or Parsins to Estimate the Relative Population Densities of Carrot Fly( Psila Rosae) Larvae, and Its Practical Application[J]. Annals of Applied Biology, 1982,100 (2) .

[9]Hardin J, Hilbe J. Generalized Linear Models and Extensions[M]. 2nd. College Station，USA: Stata Press, 2007.

(责任编辑：崔国平)

Beta-Binomial Regression and Its Application

ZHAO Wei-hua1, ZHANG Ri-quan2

(1. School of Science, Nantong University, Nantong 226019, China; 2. School of Finance and Statistics, East China Normal University, Shanghai 200241, China)

Abstract:Beta-Binomial distribution is frequently used to describe the over-dispersion count data in the success-failure type test or satisfaction ratings survey problem. In this paper, we address the Beta-Binomial regression model, and the maximum likelihood estimate method is investigated, which can be implemented by the Newton-Raphson algorithm. Furthermore, the Score test methods are proposed to test the important covariates and the existing of the correlation parameter, and their test powers are investigated by simulations. Finally, the real data analysis is used to illustrate the usefulness of Beta-Binomial regression model.

Key words:proportional data; Beta-Binomial distribution; over-dispersion; correlation

中图分类号：C81∶O212

文献标志码：A

文章编号：1007-3116(2016)03-0009-05

作者简介：赵为华，男，江苏海门人，理学博士，副教授，硕士生导师，研究方向：分位数回归建模及其应用；

基金项目：教育部人文社科青年基金项目《比例数据的分位数回归建模》(14YJC910007)

收稿日期：2015-10-23

张日权，男，山西大同人，理学博士，教授，博士生导师，研究方向：分位数回归和半参数模型。

【统计理论与方法】