不同城市的房价是否具有相同的人口集聚效应——基于35个大中城市PVAR模型的实证分析

楚尔鸣，何　鑫

(湘潭大学 商学院，湖南 湘潭 411105)



不同城市的房价是否具有相同的人口集聚效应
——基于35个大中城市PVAR模型的实证分析

楚尔鸣，何鑫

(湘潭大学 商学院，湖南 湘潭 411105)

摘要：人口集聚会引起房价上涨，但不同类型的城市由于集聚人口的教育程度不同，房价上涨也具有不同的效应。首先建立人口流动理论模型分析人口集聚对房价上涨的影响，然后通过建立房价、人口集聚、房地产投资和人均可支配收入的PVAR模型进行实证分析。结论表明，一类城市人口集聚对房价上涨具有正效应，二类城市为平效应，三类城市为负效应；三类城市的房价上涨主要是房地产投资和人均收入提高所推动的。

关键词：房价；人口集聚；PVAR

一、引言

自1998年房地产市场改革以来，中国已经步入城镇化发展的“快车道”，但伴随而来的高房价早已成为国人关注的社会问题。多年来，有关城市高房价的成因等问题一直是学术界激烈争论的焦点，但并未得出一致结论。这一方面是由于房屋具有投资品和消费品的双重属性，除了供给和需求因素外，可能还存在着其它影响房屋价格的因素；另一方面，房屋价格与土地政策密切相关，中国现有的土地政策使地方政府存在以垄断价格出让土地的可能性，从而使房价的决定和影响因素更为复杂。我们观察到的经验事实是2005年以来中国各城市房价迅速攀升，而且不同城市的房价差别迅速扩大。究竟是什么原因导致不同城市的房价差异呢？这便是本文研究的核心问题。

从现有研究文献来看，有关房价及不同城市房价差异的影响因素总体上可以概括为四类： 第一，经济因素。众多学者认为居民收入是影响房价最为重要的因素[1-3]，但是仅通过收入的高低来解释不同城市的房价，并不能达到令人满意的结果。现在越来越多的学者从收入差距角度来解释，并认为收入差距过大造成房地产投资对房价的影响也越来越大[4-5]，而贫富差距的扩大也推动人口、经济要素等过快地集中于少数几个大城市，从而进一步刺激城市房价的刚性需求[6]48-63。第二，社会因素。有的学者认为人口结构是房价上涨的重要原因，如少儿抚养比下降使得人们对房屋的需求有所增加从而抬高了房价[7]；而另有学者认为家庭结构才是房价上涨的主要原因，如有未婚男性的家庭购买住宅的可能性更高[8]。此外，还有学者认为消费心理预期、城市化建设等是推动城市房价快速上涨的主要因素[9-10]。第三，宏观调控因素。近年来国内学者围绕货币政策对房地产价格的影响、限购政策对房地产市场介入的有效性、土地财政是否导致房价的快速上涨、房产税是否能够降低住宅资产的长期均衡价格以及经济适用房对房价的调节作用等等进行了深入的讨论[11-15]。第四，环境因素。已有研究表明房价表现出明显的区位和环境特征，即越靠近商贸中心、交通越便利的区域，住房价格越高。此外，自然环境、邻里特征、建筑风格等因素都在一定程度上影响房价[16-17]。

本文认为，以上文献虽然从不同角度解释了房价上涨，但仍然不能较为系统、清晰地解释不同城市间的房价差异。因此，本文试图从人口集聚的角度予以阐释，并认为不同城市中收入的高低、住宅的供需、房地产政策的实施以及居住的环境都可以通过人口的集聚体现出来。鉴于此，本文拟从如下几个方面进行探索：在研究目的方面，将房价、人口集聚、房地产投资和人均收入纳入一个模型框架进行分析，比较不同变量在不同区域房地产市场中的作用，以研究房地产市场的区域异质性；在研究对象方面，将选用2002—2013年中国35个大中城市的年度面板数据，以精确观测不同区域房地产市场对各变量冲击的响应程度；在研究方法方面，采用面板向量自回归(PVAR)模型，以解决传统向量自回归模型中无法体现城市房价异质性的问题，并对结果进行稳定性检验，从而保证结论的有效性。

二、理论模型

人往高处走，水往低处流。促成人口从一个城市流向另一个城市的原因有许多，如个人偏好、工资收入、城市设施、事业平台、房价高低等。西方学者Saiz提出了房价与居民迁移的模型，通过模型和实证结果发现人口的迁入会提升城市的房价[18]。Sá在Saiz模型的基础上，将房屋消费的收入效应以及本地居民对人口迁入的偏好纳入模型，较好地解释了不同城市面对人口集聚时房价的波动情况[19]。

Uic=Vic+hθx1-θ-δ·I

(1)

其中，Uic是居民i在城市C获得的效用，Vic是指居民i对城市C的偏好，而h和x分别指居民i在住房和其他商品上的消费，并以Cobb-Douglas效用函数的形式给出，且0<θ<1。δ表示居民i对流入人口I的偏好，若偏好为厌恶型，则δ>0，若偏好为接受型，则δ<0。

高收入阶层的预算约束为：r·h+x=WH，其中r为租房的单位价格，为简化模型本文将商品x的价格标准化为1，WH为高收入阶层居民的收入。经过效用最大化可得住房和其他商品的需求函数：

(2)

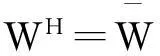
(3)

假设流入人口均偏好留在该城市，并且各个阶层的居民对房屋设施的需求均为同质，则城市居民对房屋设施的总需求为：

其对数的形式为：

lnHD=-ln2r+lnW

(4)

流入人口的住房成本以及本地居民的流动性还取决于住房供给弹性，Saiz给出的住房供给方程为[18]：

lnHS=β0+β1lnP

(5)

(6)

本文研究的重点是房价的人口集聚效应，将式(3)、式(4)和式(6)结合后可表示为：

(7)

三、变量、数据与计量模型

(一)变量选取

鉴于上述供求分析原理和指标数据的可获性，本文在研究中选取的变量主要包括价格指标(房价指标)、社会因素指标(人口集聚指标)、供给方指标(房地产投资指标)、需求方指标(人均可支配收入指标)，相应的描述和定义如下：

2.人口集聚指标(PEit)。现有国内外文献中选取衡量人口集聚的变量通常为人口密度，本文认为，现有人口密度数据并不能真实反映一个城市的人口集聚度。首先，在当今人口流动性较大的前提下，常住人口数量相比于户籍人口数量更能准确反映出一个城市人口集聚的规模和现状；其次，人口集聚更容易集中于行政区域而并非在整个城市均匀分布，若在人口密度的测算过程中使用实际土地面积，则在一定程度上会降低人口集聚程度。因此，本文通过人口集聚=常住人口数/行政区域土地面积进行测算，在测算的过程中，除了校正较为明显的统计错误之外，还需对部分数据进行调整。例如，在2002—2013年内，部分城市伴随着城镇化的进展，其行政土地面积也发生较大幅度增长。以海口市为例，2002年行政区域面积为236平方公里。而2014年则变为2 305平方公里。为了消除此类因素对于人口集聚的影响，不妨假定其行政区域面积不变进行大致估计。测算后部分城市的人口集聚与以人口密度为代表的人口集聚对比如图1所示。从结果来看，测算后的人口集聚水平更加平稳，且一、二线城市人口集聚程度基本上高于测算前的程度，而三线城市和部分二线城市人口集聚程度则有不同程度的变化，这在一定程度上提高了城市等级与人口集聚的倾斜度。鉴于此，本文将以35个大中城市年度常住人口与行政区域面积的比值来表示人口集聚指标(单位：人/平方公里)，并取其自然对数的形式，记为lnPEit。

3.房地产投资指标(HIit)。用35个大中城市住宅类房地产投资来表示(单位：亿元)，并取自然对数的形式，记为lnHIit。

4.收入指标(INCit)。考虑到房价主要是由城镇房屋住房价格来衡量，因此本文不再将农村居民人均纯收入纳入指标进行考察，仅采用35个大中城市城镇居民人均可支配收入来表示(单位：元/人)，并取自然对数的形式，记为lnINCit。

(二)数据来源

本文使用2002—2013年中国35个大中城市年度面板数据进行分析。数据主要来源于万德(wind)数据库、《中国城市统计年鉴》与国家和地方政府统计局官方网站。其中，对于部分缺失数据通过指数平滑法进行估测，各个变量的描述性统计如表1所示。

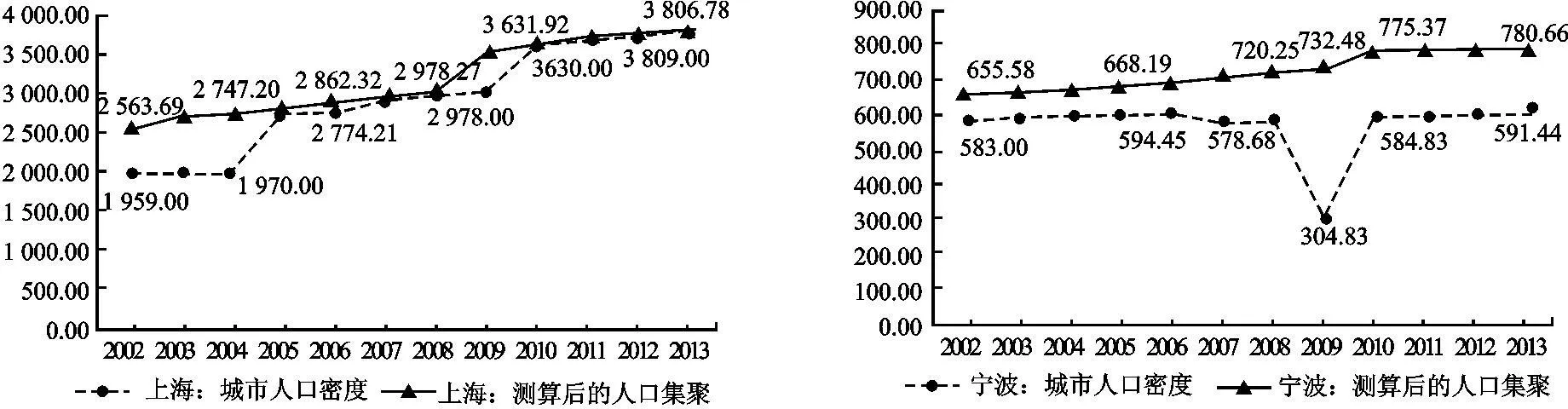
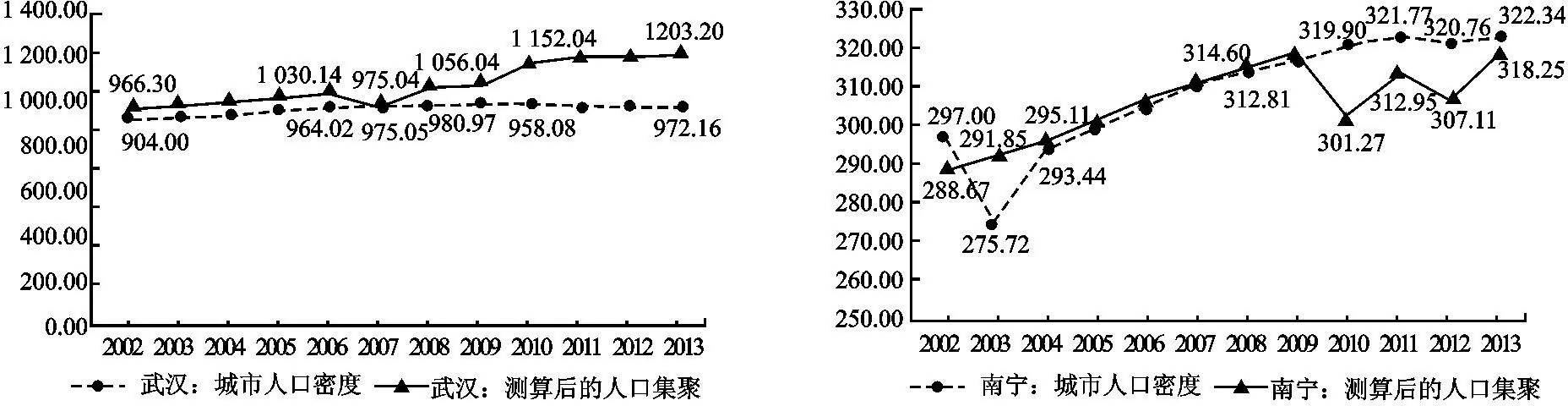
图1　不同城市测算前与测算后的人口集聚图

①根据国务院发布的《关于调整城市规模划分标准的通知》,文中将一线城市与二线发达城市划分为一类城市，包括北京、上海、广州、深圳、天津、杭州、南京、济南、重庆、青岛、大连、宁波和厦门共13个城市。②二类城市包括成都、武汉、哈尔滨、沈阳、西安、长春、长沙、福州、郑州、石家庄和太原共11个城市。③三类城市包括合肥、南昌、南宁、昆明、乌鲁木齐、贵阳、海口、兰州、银川、西宁和呼和浩特11个城市。

(三)数据的平稳性检验

本文针对五个变量的数据进行了平稳性检验。使用Stata12根据AIC最小值选择最佳滞后阶数后，对各变量进行LLC(Levin-Lin-Chu)检验和IPS(Im-Pesaran-Shin)检验，检验后，lnHP、lnPE、lnEA、lnHI四个变量在1%的显著水平下平稳，而变量lnINC在1%的显著水平下无法拒绝面板包含单位根的原假设，但其一阶差分的数据在10%的显著水平下平稳，检验结果如表2所示。

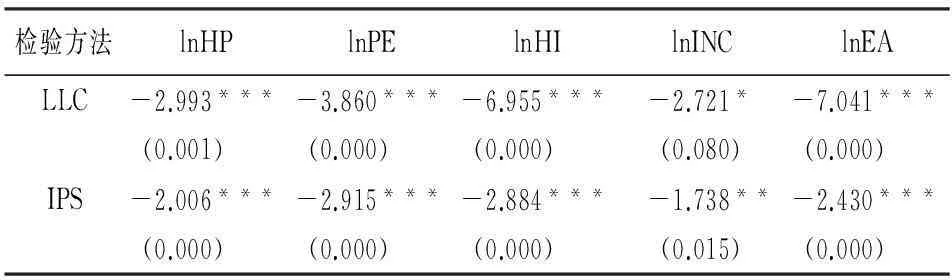
表2　面板单位根检验

注：***、**、*分别表示在 1%、 5%、 10%的显著性水平下拒绝存在单位根的原假设。

(四)滞后阶数的确定与模型的构建

将“毕业论文”中所有图的适当位置插入图标题或表格标题。按长文档格式要求，第一章的图编号格式为“图1－1、图1－2…..”。选中“毕业论文”第一章节的第一个图，选择“引用”菜单中的“插入题注”，选择“新建标签”，新建一个“图1-”标签，就可以插入一个“图1-1”的题注，然后再输入图的说明文字。再次插入图的题注的添加方法相同，不同的是不用新建标签了，直接选择插入就可以了。Word会自动按图在文档中出现的顺序进行编号。

传统的向量自回归模型对于区分外生变量和内生变量非常有效，但是要求数据具有较长的时间序列。同时，房价在不同的城市差异较大，个体之间的异质性较为明显。Holtz-Eakin等认为，PVAR模型一方面可以解决数据不足的问题，另一方面也可以在模型中体现出各个城市的异质性[21]。为了估计房价、人口集聚度、房地产投资和人均收入四个变量的PVAR模型，本文将首先检验模型的滞后阶数，全国和三类城市模型中的滞后阶数可以参考AIC、BIC和HQIC三个准则，结果如表3所示。由结果可知，全国、一类城市和二类城市的PVAR模型的滞后阶数取1比较合适，而三类城市的PVAR模型的滞后阶数取2较为合适。

鉴于上述结果，本文定义35个大中城市房价的PVAR模型形式如下：

(8)

注：*表示在该准则下建议的阶数。

其中，Yit表示第i个城市第t期的内生变量，Yit=(lnHPit,lnPEit,lnHIit,lnINCit)’，其中全国、一类和二类城市的模型中滞后阶数p=1，而三类城市的模型中滞后阶数p=2。另外，μit为模型的随机扰动项，Ψt为模型的时间效应，fi为模型的个体效应。为消除模型中的两类效应，采用截面均值差分法消除Ψt和向前均值差分法即Helmert转换消除fi，以此消除滞后项与随机扰动项之间的相关性，从而更加精准地估计模型的参数[22]。然后，利用系统广义矩估计SGMM对模型进行估计，并用蒙特卡洛过程进行脉冲响应分析和方差分解，将人口集聚变量放入模型中进行稳定性检验，以此描述房价与人口集聚的相互影响。

四、实证结果及分析

(一)PVAR模型的估计

本文首先构建一个包含房价、人口集聚、房地产投资和人均收入的PVAR模型，并且根据不同的截面选取不同滞后阶数，并对以上数据进行面板向量自回归GMM估计，估计结果如表4、表5、表6和表7所示。需要说明的是，PVAR模型中引入过多的变量的滞后期往往导致模型中的参数不显著，但这并不妨碍结论，因为VAR模型通常的主要用途是预测分析。首先，从房价对数(lnHP)方程中可知，房价易于受其自身的影响，其滞后一期的房价系数均在0.77以上。另外，在全国或者一类城市中，影响房价的主要因素为人口集聚，其系数分别为0.99和1.11，且均在1%的显著水平下是显著的，而二、三类城市的房价则更易于受到房地产投资的影响。其次，从人口集聚对数(lnPE)方程中可知，除去自身的惯性效应，人均收入是人口集聚的一个重要指标，从全国范围来看，人均收入的系数为0.14，影响程度仅次于其自身，这与一、二类城市的结果几乎一致，不过在三类城市中，人均收入的系数却最小，说明人均收入并非是人口集聚的主要原因。再次，从房地产投资对数(lnHI)方程来看，房地产投资受到人口集聚影响的系数并不显著，同时，一类城市中房地产投资仅受其滞后一期的影响较为显著，其系数值达到了1.07，而二、三类城市中除了主要受其自身的影响外，人均收入也在一定程度上影响房地产投资，不过其影响系数却为-0.84和-0.16，人均收入较低的城市房地产投资的吸引力越来越大。最后，从人均收入对数(lnINC)方程来看，人口集聚对人均收入影响最大，且从全国和一、二类城市来看，其影响系数均为正；但从第三类城市来看，其影响系数却为负。

表4　全国房价的PVAR模型的参数估计结果

注：***、**、*分别表示在 1%、 5%、 10%的显著性水平下拒绝存在单位根的原假设，h_表示一阶滞后。表5、表6同此。

表5　一类城市房价的PVAR模型的参数估计结果

表6　二类城市房价的PVAR模型的参数估计结果

表7　三类城市房价的PVAR模型的参数估计结果

(二)脉冲响应分析

PVAR模型的分析重点是脉冲响应和方差分解。脉冲响应的原理是指在现有模型基础上，某一个方程的随机扰动项发生一个标准差变化后，模型中其余内生变量受到其冲击后在未来各期的响应情况。通过蒙特卡洛(Monte-Carlo)500次模拟，将冲击时间设置为18期，可以得到房价及其他变量的脉冲响应函数图。模拟结果经整理后如图2所示。

图2房价对不同变量冲击的响应图

从图2中人口集聚对房价的冲击来看，全国房价对于人口集聚的冲击具有正向响应，且在第三期达到最大值0.04，之后其脉冲响应值逐渐平稳趋于0。分城市来看，第一类城市的房价脉冲响应值始终为正，并在第4期达到最大值0.06，显然比全国的房价脉冲响应值更为明显，说明第一类城市存在大量人口净流入，人口集聚对房价上涨产生正效应。这是因为在经济较为发达的城市中，土地资源紧张，用于建设住宅的土地相对匮乏，住房供应受限，人口净流入的集聚效应导致对住房的刚性需求量大，自然会造成房价的迅速攀升。第二类城市的房价脉冲响应值虽然在初期达到最大值0.01，但是之后转变为负数，且脉冲响应值的变化幅度始终较小。说明第二类城市的人口集聚对房价上涨是平效应，说明第二类城市的人口净流入少，人口集聚所形成的住房需求与住房供给大体持平。第三类城市的脉冲响应值在初期为负，并在第6期达到最小值-0.19，其响应值直至第13期后才显示为正，而后逐渐趋于平稳。说明第三类城市的人口净流入更少或可能为负，人口集聚所形成的住房需求量小于供给量，因此人口集聚对房价上涨产生负效应。同时，不同城市中人口结构和受教育程度不同，一类城市中受过高等教育的人数往往数倍于二、三类城市中拥有的数量，以2013年各城市高等院校学生人数为例，在平均每10万人口中，北京市和上海市分别为5 469人和3 421人，中部省份的人数在2 400人左右，而绝大多数的西部省份人数则为2 000人左右，其中新疆、西藏、青海、云南和贵州5个省市区甚至低于1 700人。由于流入不同城市的人口所受教育程度的差异，当人口流入第三类城市时，并没有引起住宅需求的增加，这种现象使得房价难以上升甚至下滑，从而成为三类城市人口集聚对房价上涨产生负效应的一个原因。

从图2中房地产投资对房价的冲击来看，脉冲响应值均为正，说明房地产投资在不同城市中对房价上涨具有正向推动作用，而且三类城市更为明显，第7期达到最大值0.23，表明三类城市的房价上涨主要是投资推动的。从图1中人均收入对房价的冲击来看，第一类和第二类城市的房价对于人均收入的冲击，其脉冲响应值均在第3期达到最小值-0.05，而第三类城市的脉冲响应值在第二期达到最大值0.04，说明第一、二类城市的人均收入对房价上涨具有负效应，而第三类城市则为正效应。这其中一个可能的原因是生活成本与房价泡沫。从Mercer公司发布的211个城市生活成本排行榜来看，上海、北京、青岛、成都等一、二线城市均在列，由于食品价格上升、人民币升值和房屋需求旺盛等原因引起城市生活成本逐年上升，物价上涨的速度远高于收入增长的速度。另外，由于一、二线城市房价易于产生房价泡沫，收入的增加实质上让人们的生活压力更大，反而更加降低了对住宅的需求。同时，由于第三类城市中生活成本和房价泡沫都远不及第一、二类城市，人均收入的增加会刺激人们对住宅的需求，造成房价的迅速攀升。

(三)方差分解

方差分解的结果如表8所示。全国房价方差贡献率在第1期全部来自自身，在第10期自身对方差的贡献率还有62.8%。在第一类城市中，人口集聚对房价方差的贡献率在第五期达到13.7%，第10期达到20%。是除房价自身外，在其它因素中贡献率最大的因素。在第二类城市中，房地产投资的贡献率较大，第5期和第10期分别达到18%和24.5%，人口集聚的贡献率仅占9.4%。在第三类城市中，虽然在第5期房地产投资的贡献率较大，达到38.9%，但到第10期，人口集聚又是除房价自身外，贡献率最大的因素，达到25.7%。方差分解结果表明，人口集聚对第一类城市和第三类城市房价的方差贡献率是比较大的，而对第二类城市房价的方差贡献率较小，这与理论分析和脉冲响应的结论是相符合的。从人口集聚的方差分解来看，全国第1期的方差贡献率主要来自于自身和房价，其余变量的贡献率均为零；在第5期和第10期，只有人均收入的贡献率增加，房地产投资对人口集聚的方差贡献率仍然为零。从城市分类来看，人口集聚的方差贡献率主要来自自身，其次是房价，再次是人均收入，最低是房地产投资，这一顺序在第一、二、三类城市中都是一致的。这说明高房价是人口流出的重要影响因素，而高收入是人口流入的重要影响因素。

表8　面板误差项方差分解表

(四)稳健性检验

为检验上述结果的稳健性，本文基于人口集聚导致经济集聚的思想来进行稳健性检验。国内学者近年来的研究文献中，代表经济集聚的指标主要有：人均GDP或地均GDP、区位熵、所有产业市场份额的平方和等。本文选用35个大中城市地均GDP来表示经济集聚(单位：万元/平方公里)，并取自然对数的形式，记为lnEAit。

在PVAR模型中由于内生变量与其误差项之间存在相关性而导致系数的估计值出现偏差。Arellano和Bond采用差分广义矩(Difference GMM)的方法，即将所有可能的滞后变量作为工具变量对其差分方程进行GMM估计，以消除动态面板模型中变量与随机扰动项之间的相关所产生的估计偏差，从而有效地对参数进行估计[23]。

考虑到在脉冲响应分析中房价自身会对下一期的房价产生影响，因此在构建动态面板模型对方程进行稳健性检验时，我们将房价的滞后二期作为其中的解释变量，并且采用两步广义矩(Two-step GMM)对参数进行估计。需要说明的是，由于分类城市中第二类城市和第三类城市的样本量不足100，因此稳定性检验中的对象为全国和第一类城市的房价方程。另外，根据马克思关于劳动生产率与劳动报酬份额的理论，经济越发达的地区人均收入也越高，在稳定性检验中，选用经济集聚变量替代人均收入变量后的结果如表9所示。

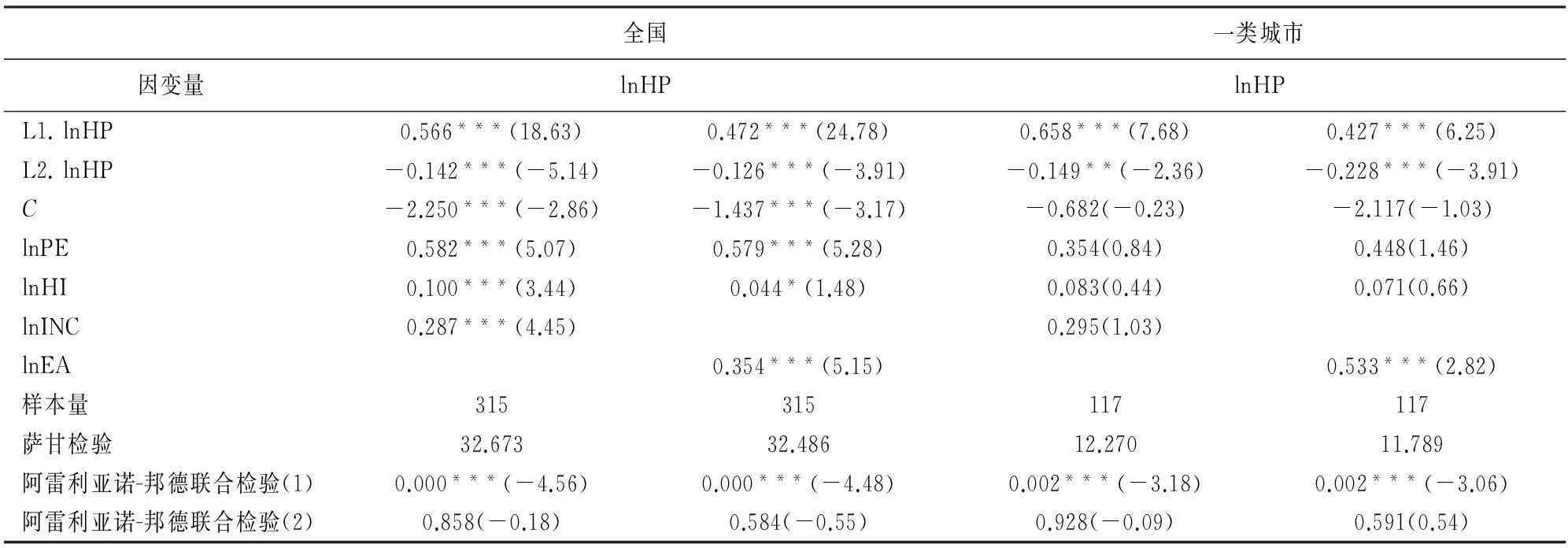
表9　动态面板模型稳健性检验结果

注：***、**、*分别表示在 1%、 5%、 10%的统计显著性水平拒绝原假设。各变量括号中为z统计量，Sargan检验中各数值的P值均为1，表明无法拒绝工具变量均有效的假设。Arellano-bond检验结果表明模型中扰动项的一阶差分存在自相关，而二阶或高阶不存在自相关，从而表明方程中扰动项无自相关，可以接受差分GMM的估计。

从动态面板的检验结果来看，与前面的模型估计结果基本一致，人口集聚的确是影响房价的一个主要因素。而采用经济集聚变量替代人均收入变量后，大致的结果仍不发生改变，回归系数比较相近，说明本文结论具有较好的稳健性。

五、结论与政策建议

本文通过35个大中城市2002—2013年房屋住宅销售价格、人口集聚、房地产投资和城镇居民人均可支配收入的数据，应用PVAR模型中的GMM估计、脉冲响应分析和方差分析，按城市划分后对四者之间的相互关系进行了检验。研究发现不同城市中人口集聚对房价具有不同的效应：第一，第一类城市人口集聚对房价上涨产生正效应，第二类城市为平效应，第三类城市为负效应。第二，人均收入高是人口流入的重要影响因素，而高房价则是人口流出的主要原因。第三，第三类城市的房价上涨主要是房地产投资和人均收入提高所推动的。

鉴于上述研究结果，从供给端来看，第一类城市政府应提供更多的保障性住房，加快经济适用房、廉租房的投入与使用，保障居民有房可住；而对第三类城市则应合理控制住房的供给，合理利用土地资源，降低住房空置率，避免出现“鬼城”现象。从需求端来看，第一类城市应适度控制人口净流入，防止房价上涨过快，同时对拥有多套住房的本地居民或外地投资者，政府也应当落实限购政策，严格征收房产税。而且政府应当合理分流人口，鼓励人口流向三、四线城市，在加快三、四线城市建设和小城镇建设的同时，出台当地城镇化的优惠政策，增加就业岗位，改善居住环境，提高居民生活水平。总之，对不同类型的城市实施更具针对性的宏观调控政策、人口流动政策和城镇化政策，将房价控制在合理的区间，既防止快速上涨，又防范急剧下跌，保证国民经济实现稳定、协调和可持续增长。

参考文献：

[1]Harter-Dreiman, Michelle. Drawing Inferences About Housing Supply Elasticity from House Price Responses to Income Shocks[J]. Journal of Urban Economics,2004,55(2).

[2]Gallin, Joshua. The long-run Relationship Between House Prices and Income: Evidence from Local Housing Markets[J]. Real Estate Economics,2006,34(3).

[3]沈悦,张学峰,周奎省. 住宅价格与居民收入均衡关系及住房支付能力稳定性[J]. 财经研究,2011(3).

[4]陈健,高波. 收入差距、房价与消费变动——基于面板数据联立方程模型的分析[J]. 上海经济研究,2012(2).

[5]高波,王文莉,李祥. 预期、收入差距与中国城市房价租金“剪刀差”之谜[J]. 经济研究,2013(6).

[6]刘忠良. 大国危途——民族兴衰与人口政策再思考[M]. 北京:经济科学出版社,2013.

[7]徐建炜,徐奇渊,何帆. 房价上涨背后的人口结构因素:国际经验与中国证据[J]. 世界经济,2012(1).

[8]谢洁玉,吴斌珍,李宏彬,郑思齐. 中国城市房价与居民消费[J]. 金融研究,2012(6).

[9]张亚丽,梁云芳,高铁梅. 预期收入、收益率和房价波动——基于35个城市动态面板模型的研究[J]. 财贸经济,2011(1).

[10]陆铭,欧海军,陈斌开. 理性还是泡沫:对城市化、移民和房价的经验研究[J]. 世界经济,2014(1).

[11]王来福,郭峰. 货币政策对房地产价格的动态影响研究——基于VAR模型的实证[J]. 财经问题研究,2007(11).

[12]张岑遥. 城市房地产价格中的地方政府因素:成因、机制和效应[J]. 中央财经大学学报,2005(10).

[13]严金海. 中国的房价与地价:理论、实证和政策分析[J]. 数量经济技术经济研究,2006(1).

[14]况伟大,朱勇,刘江涛. 房产税对房价的影响:来自OECD国家的证据[J]. 财贸经济,2012(5).

[25]刘广平,陈立文,许海平. 经济适用房能降低房价吗?——基于经济适用房供给量的调节作用分析[J]. 中央财经大学学报,2015(2).

[16]杨君伟,胡燕京. 中国典型城市房价上涨和自然环境级差因素的相关性分析[J]. 华东经济管理,2007(11).

[17]蔡真,汪利娜. 住宅市场的价格特征:以北京为例[J]. 金融评论,2012(6).

[18]Saiz, Albert. Immigration and Housing Rents in American Cities[J]. Journal of Urban Economics,2007, 61(2).

[19]Sá F. Immigration and House Prices in the UK[J]. Economic Journal, 2015，125(587).

[20]Ottaviano G, Peri G. The Effects of Immigration on US Wages and Rents: A General Equilibrium Approach[J]. Cepr Discussion Papers, 2007, 39(4).

[21]Holtz-Eakin D, Newey W, Rosen H S. Estimating Vector Autoregressions with Panel Data[J]. Econometrica: Journal of the Econometric Society, 1988,56(6).

[22]Arellano M, Bover O. Another Look at the Instrumental Variable Estimation of Error-Components Models[J]. Journal of Econometrics, 1995, 68(1).

[23]Arellano M, Bond S R. Some Test of Specification for Panel Data : Monte Carlo Evidence and an Application to Employment Equations[J]. Review of Economic Studies, 1991, 58(2).

(责任编辑：马慧)

Does the House Price in Different Cities Have the Same Population Agglomeration Effect：Empirical Analysis Based on PVAR Model of Thirty-five Large and Medium Scale Cities

CHU Er-ming，HE Xin

(School of Business，Xiang Tan University, Xiangtan 411105, China)

Abstract:The gathering of population will raise house price, house prices also have different effects on different types of cities due to the different education degree. First, this paper establishes the population mobility theory model to analyze the effect of population concentration on the rise of housing price. Then the PVAR model, set up on real estate price, increasing population, investment in real estate and the per capita disposable income, is analyzed empirically. The analysis indicates that resident agglomeration in the first-tier cities has positive effect, and flat effect on second-tier, negative effect on third-tier cities. The major motivation of house price raises in third-tier cities is that the investment of real estate and the increases of per capita income.

Key words:housing prices; population agglomeration; PVAR

中图分类号：F224.0

文献标志码：A

文章编号：1007-3116(2016)02-0081-09

作者简介：楚尔鸣，男，湖南湘潭人，工学博士，教授，博士生导师，研究方向：宏观经济政策；

基金项目：国家自然科学基金项目《空间非一致性、房地产价格波动与最优货币政策选择研究》(71273221)

收稿日期：2015-09-11

何鑫，男，湖南长沙人，博士生，研究方向：金融统计与宏观经济政策。

【统计应用研究】