弯曲载荷作用下复合材料T型接头的失效分析*

吴　海，肖加余，邢素丽，文思维，杨孚标，杨金水

(国防科技大学 航天科学与工程学院， 湖南 长沙　410073)



弯曲载荷作用下复合材料T型接头的失效分析*

吴海，肖加余，邢素丽，文思维，杨孚标，杨金水

(国防科技大学 航天科学与工程学院， 湖南 长沙410073)

摘要：运用蔡-吴逐步失效判据和黏聚接触模型建立弯曲加载下的T型接头的有限元模型。对复合材料T型接头在弯曲加载下的损伤机理和承载能力进行数值模拟。结合静态弯曲加载实验，揭示T型接头在弯曲破坏过程中的四种失效模式。T型接头的弯曲失效载荷的有限元模型计算结果与实测值吻合较好。

关键词：T型接头；蔡-吴逐步失效判据；黏聚接触模型；失效模式；弯曲失效

复合材料接头是复合材料结构件中连接部件、传递载荷的一种重要结构形式，因其可以有效地减轻结构重量，提高连接效率，而在船舶和航空复合材料构件中得到广泛运用，其中T型接头作为典型整体成型构件中最薄弱的部位，吸引了国内外众多研究者的关注。Shenoi的团队[1-5]最早开展了船舶复合材料构件中的T型接头的损伤研究，考察了结构参数和材料参数对其力学性能的影响，并通过有限元分析的方法确定其损伤容限。Orifici等[6]通过有限元方法分析了碳纤维/环氧复合材料T型接头在后屈曲过程中可能发生的损伤模式。Stickler等[7-9]研究了横向缝合的碳纤维复合材料T型接头的拉伸、弯曲和剪切力学性能，发现植入的纤维可以有效提高T型接头的弯曲性能，但对其拉伸和面外剪切性能起不到同样的效果。Koh等[10-12]重点关注了z-pin增强碳纤维复合材料T型接头的力学性能和增强机理，通过阻止裂纹扩展可以有效提高T型接头的极限强度、失效位移和吸能能力。Park等[13]则进一步通过实验研究碳纤维z-pin的直径和填充密度对T型接头的剥离强度的影响。Burns等[14-15]从树木的“枝-杆”模型中得到启发，对T型接头搭接部分植入底板的比例和L型筋条的铺层角进行优化，以提高T型接头的承载能力和弯曲加载下的断裂韧性。Engelstad等[16-18]开发了计算成本较小但精度高的高阶积分单元族对F-35战机中应用的T型接头进行模拟计算。Wagner等[19]首次采用黏聚区模型对T型接头的裂纹引发和扩展进行模拟。

国内研究工作开展较晚，白江波等[20]和罗楚养等[21]分别对树脂传递模塑工艺成型复合材料T型接头的工艺参数优化和疲劳性能进行了实验研究。谢富原和王雪明等[22-23]则对碳纤维/双马来酰亚胺复合材料T型接头的热压罐工艺进行了研究。崔浩等[24]采用单元离散方法在T型接头的层间界面以及填充区内部插入黏聚区单元，确定了拉伸载荷下T型接头的失效模式为Ⅰ/Ⅱ混合型模式。

相比拉伸载荷，弯曲载荷是T型接头更普遍的受载方式。从国内外已公布的文献来看，尚缺乏针对T型接头在弯曲载荷作用下的力学行为和损伤机理的系统研究。

1有限元模型

1.1损伤失效准则

在研究复合材料层合板的层间失效和面内失效时分别采用了黏聚区模型和蔡-吴逐步失效判据，并根据这两种损伤失效准则建立弯曲载荷作用下的T型接头的有限元模型。

黏聚区模型[25]是基于弹塑性断裂力学用于模拟复合材料层间失效的一种常用方法，提出在裂纹尖端有一个微小的塑性屈服区，即所谓的黏聚区。塑性区内的应力-位移曲线遵循着几种特定的关系函数，如双线性、梯形、多项式及指数等损伤本构关系函数。目前普遍应用双线性本构模型[26-27]，首先在预定的分层裂纹或脱黏路径上插入一层黏聚单元，当载荷增大至临界点后开始损伤演化，进入刚度线性退化阶段；刚度减小为零时，黏聚单元完全失效并被删除，即构件中出现分层裂纹，其本构模型如图1[28]所示。黏聚区模型能够比较直观地预测裂纹的起始和扩展过程，操作简便，物理意义明晰。

图1　双线性本构模型Fig.1　Bilinear cohesive constitutive model

蔡-吴逐步失效判据是评估复合材料层合板面内失效的一种可靠方法，预测结果的准确性较高，其失效判据因子R的一般通式为：

R=Fiσi+Fijσiσj+Fijkσiσjσk+…≤1

(1)

对于平面应力状态，式(1)中i，j，k=x，y，s。在工程设计中，通常仅选取张量多项式的前两项，而Fxs=Fys=Fs=0，因此平面应力状态下，失效准则的展开式为：

(2)

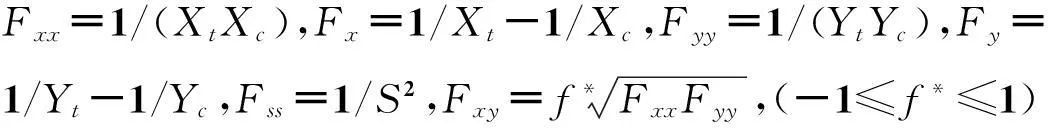
1.2结构参数

复合材料T型接头的结构尺寸及实物如图2所示，包括两个L型筋条(Ply1人，Ply2)、三角区填充带(fillet)以及底板(Ply3，Soleplate)，L型筋条则由垂直筋条部分(centerplate)和与底板黏接的水平搭接部分(overlaminate)组成。各部位的结构尺寸和铺层情况见表1，两个L型筋条与底板之间的三角区根据其缝隙体积,填充一定量的预浸料单向带。

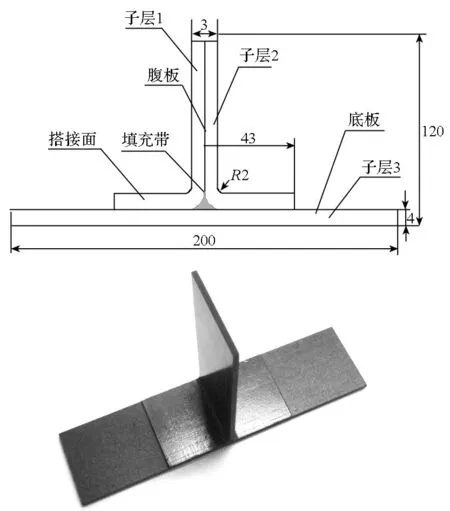
图2　T型结构件的结构图与实物图Fig.2　Structural design drawing and real photograph of T-joint

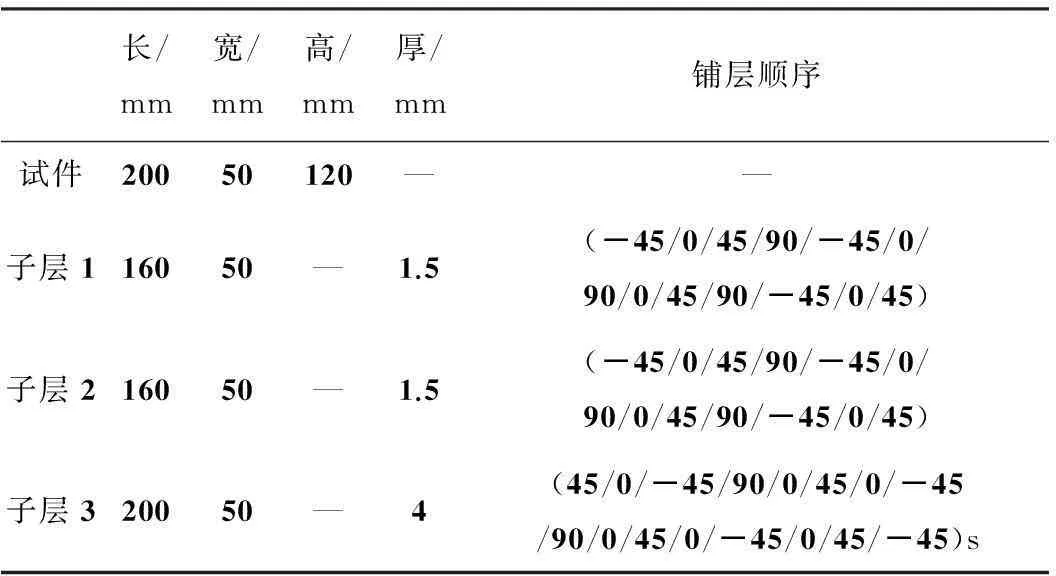
长/mm宽/mm高/mm厚/mm铺层顺序试件20050120——子层116050—1.5(-45/0/45/90/-45/0/90/0/45/90/-45/0/45)子层216050—1.5(-45/0/45/90/-45/0/90/0/45/90/-45/0/45)子层320050—4(45/0/-45/90/0/45/0/-45/90/0/45/0/-45/0/45/-45)s

1.3材料参数

复合材料T型接头采用热压罐整体成型工艺制备，原材料体系为T700/QY9611双马来酰亚胺预浸料，其单向板的力学性能参数见表2，由中航集团北京航空制造工程研究所提供。

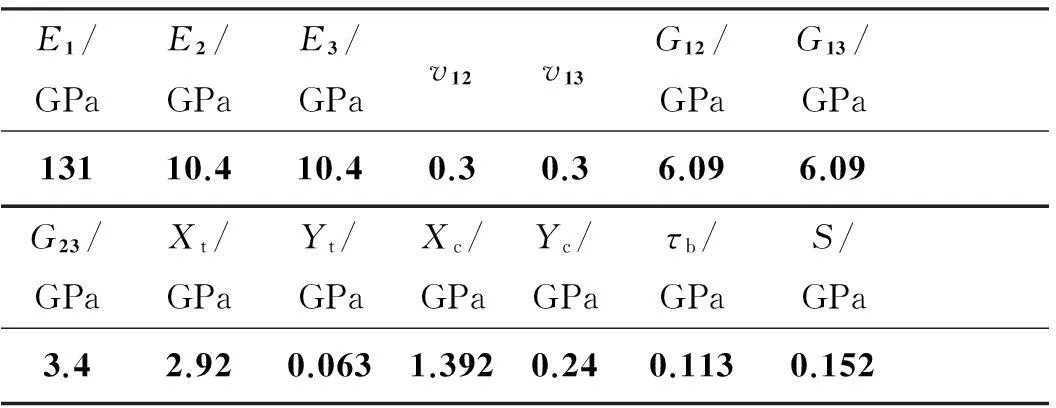
表2　T700/QY9611复合材料单向板的性能参数

注：Ei为复合材料层合板i方向上的杨氏弹性模量；vij为复合材料层合板ij面内的泊松比；Gij为复合材料层合板ij面内的剪切模量；Xt，Yt分别为复合材料层合板X，Y方向上的拉伸强度；Xc，Yc分别为复合材料层合板X，Y方向上的压缩强度；τb和S分别为复合材料层合板的层间剪切强度和纵横剪切强度。

黏聚区的参数取决于树脂基体的性能。由于QY9611树脂难以制备成浇铸体进行性能测试，而其力学性能与QY8911树脂处于同一水平，因此，计算模型材料参数直接引用文献[24]报道的QY8911双马来酰亚胺树脂的性能参数，见表3。

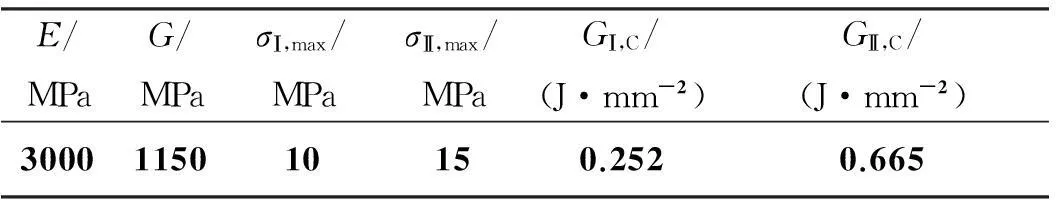
表3　QY8911双马来酰亚胺树脂的性能参数[24]

注：E为树脂基体的杨氏模量；G为树脂基体的剪切模量；σⅠ，max和σⅡ，max分别为法向的拉伸强度和两个切向的剪切强度；GⅠ，C和GⅡ，C分别为Ⅰ型断裂和Ⅱ型断裂的临界能量释放率。

1.4网格划分

采用ABAQUS有限元软件建立了T型接头的三维有限元模型进行失效预测和应力分析，如图3所示。模型的边界条件依据弯曲实验测试条件而定，在L型筋条垂直段一侧距底板80 mm处施加竖直向下运动的集中载荷，并对试件的底部两侧距离边缘10 mm处的节点进行固支。

基于蔡-吴准则预测L型筋条和底板复合材料层合板的面内失效，采用实体壳单元对L型筋条和底板离散化，L型筋条厚度方向划分为三层单元，底板厚度方向划分为四层单元，单元的堆垛方向均为层合板的实际铺叠方向(层合板板面法向)，L型筋条倒角的圆弧段一般至少要划分20个单元。

如图3所示，三角区构型非常复杂，单元划分后包含很多畸变率较大的锐角单元，容易导致计算过程中出现奇异点，结果难以收敛。因此对三角区进行简化处理，忽略三角区内部的随机裂纹扩展问题，采用实体壳单元进行划分，单元的堆垛面为三角区侧面，从而得到其侧面的应力云图。

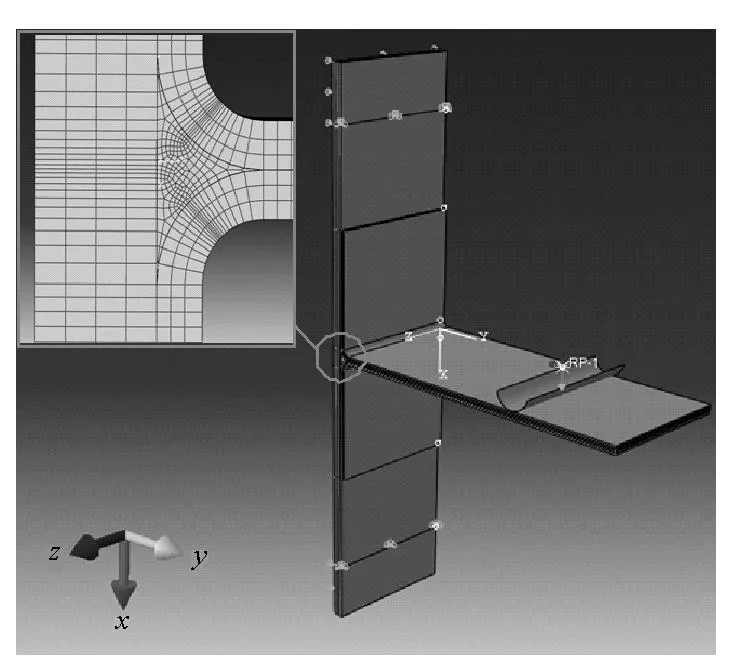
图3　复合材料T型接头的弯曲加载有限元模型Fig.3　FEM model of composite T-joint under bending load

基于黏聚区模型预测L型筋条与三角填充区和底板之间的分层失效。插入黏聚单元会引入额外的自由度，增加计算成本和收敛难度。为了简化模型，只在T型接头各子层层合板之间的界面上定义基于黏聚区失效准则的接触属性，接触属性参数见表3。

2结果与讨论

2.1T型接头在弯曲加载过程中的载荷-位移曲线

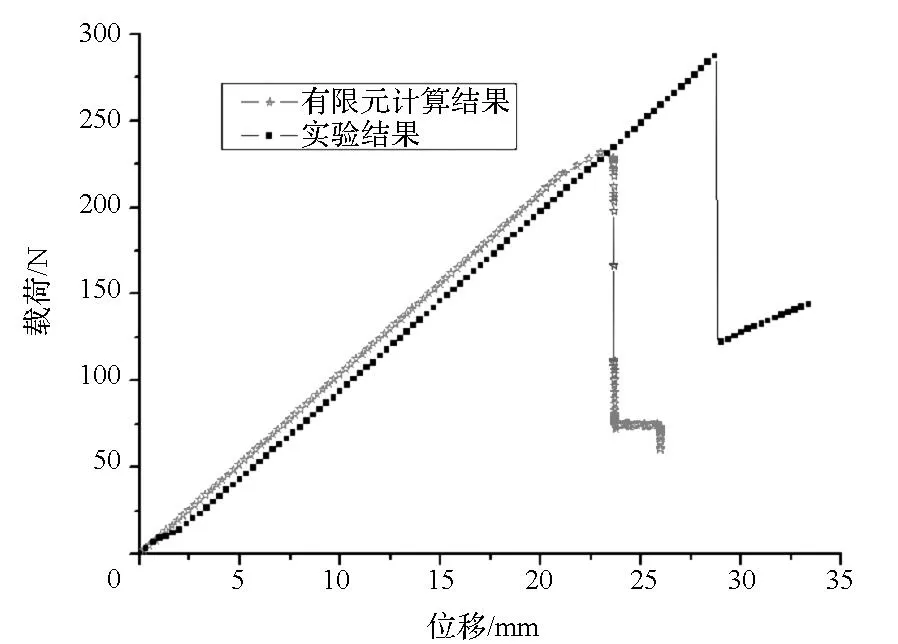
图4　复合材料T型接头弯曲加载下的载荷-位移曲线Fig.4　Load-displacement curve of composite T-joint under bending load

通过模拟和实验得到的T型接头在弯曲加载过程中的载荷-位移曲线如图4所示。有限元结果预测T型接头所能承受的最大弯曲载荷为231.4 N，而实测的最大承载则达到288.5 N。实际测试曲线在达到极限载荷前表现为稳定的线性阶段，达到极限载荷后迅速衰退到较弱的水平。对比可见，有限元模拟与实际测试曲线预测得到的刚度结果相近，但预测的强度极限相差较大。

有限元模型的计算强度明显低于实测弯曲强度，主要是因为黏聚区参数的选取较为保守，而QY9611树脂基体的实际性能参数应高于估计值。同时，有限元模型的结构仍存在一定局限性，实际弯曲加载时T型接头三角形关键区域承受大部分的拉伸、压缩和剪切作用，其内部应力分布和裂纹扩展模式极为复杂，而目前的模型只假定T型接头在弯曲加载下裂纹沿着L型筋条和三角填充区的层间界面扩展，无法考虑三角区内部随机裂纹扩展、界面裂纹偏转以及纤维拔出等一系列增韧因素，在后续工作中还需要对模型进一步地改进。

2.2弯曲加载下T型接头的逐步失效分析模拟

图5显示的是弯曲加载过程中复合材料T型接头蔡-吴失效判据因子的分布云图以及界面分层情况。

如图5(A1)所示，在加载初期，L型筋条主要承受压头施加的弯矩作用，在垂直于底板的筋条根部出现应力集中现象，此时层间界面保持完整，三角区右侧尖端同样承受较大的内应力。

Deflection=4.1 mm

Deflection=9 mm

随着弯曲载荷逐渐增大，处于三角区上方的尖角部位与L型筋条倒角圆弧段的界面处产生初始裂纹，如图5(B2)所示，此时整个倒角圆弧段附近的L型筋条都承受弯矩作用，其内部子层的蔡-吴判据因子超过临界值1，三角区应力集中区也明显扩大。可以得知，当弯曲挠度达到一定程度，虽然载荷未超过临界值，但在三角区上方与L型筋条的层间界面上已经引发比较明显的层间裂纹，同时L型筋条和三角区内部可能发生了面内的纤维或基体失效。

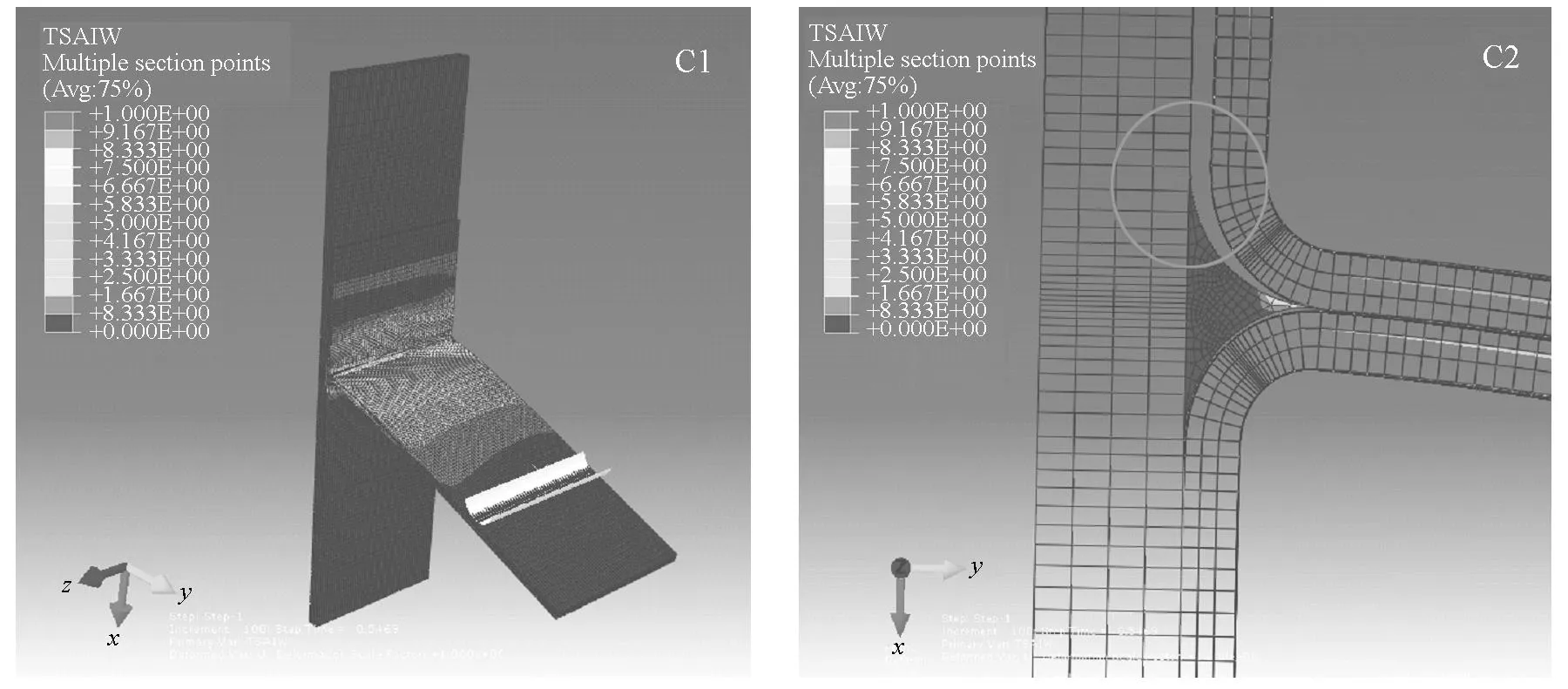
Deflection=18 mm图5　T型接头承受弯曲载荷时的蔡-吴失效判据因子分布云图和层间失效情况Fig.5　Tsai-Wu failure criterion factor distributions and interfacial failure of composite T-joint under bending load

加载后期，随着L型筋条与三角区的层间界面的解离，应力向上传递到L型筋条与底板的搭接部分，如图5(C1)所示。由于三角区实际已发生破坏或与L型筋条应力集中部位相分离，三角区内部应力逐渐减小，此时T型接头的承载能力主要由L型筋条与底板的胶结力以及L型筋条的抗弯能力提供。一旦L型筋条发生屈曲或与底板剥离，则会导致T型接头承载能力突降。

可以看出，在弯曲载荷的作用下，T型接头的失效关键部位为三角填充区及其相邻的L型筋条倒角圆弧段，其失效方式为首先在三角区上方与L型筋条的层间界面引发分层失效。值得注意的是裂纹在载荷上升到极限以前触发，沿着倒角圆弧区的界面扩展，同时还可能发生L型筋条子层内部或三角区的面内纤维或基体失效。直至临界载荷以后，上侧的L型筋条倒角圆弧段与三角区填充区完全分离，T型接头的承载能力急剧衰退。

2.3弯曲加载下T型接头的失效模式实验观察

对比分析有限元结果和实验观测结果，有限元设定裂纹扩展路径相对固定，而由于制备T型接头的不同部位的性能弱化，如层间弱黏、填充物刚度差异等因素，实际弯曲载荷作用下T型接头的失效模式主要分为以下四种。

Mode Ⅰ是L型筋条与三角区的层间界面的脱黏失效，如图6(a)所示。裂纹由三角区顶端与L型筋条的界面处引发，并沿着倒角圆弧区的边缘向三角区左侧扩展。由于三角区内部填充的卷绕单向带结构在尖角处较容易断裂，所以裂纹一般沿界面扩展到一定程度，可能会偏离层间界面而进入三角填充区内部。裂纹尖端主要承受层间剥离和层间剪切作用。

Mode Ⅱ是L型筋条子层内部的分层失效，如图6(b)所示。一般多处分层同时引发，沿着倒角圆弧向L型筋条左侧扩展，若邻近分层裂纹处有90°方向铺层，则裂纹极易偏转到其他子层界面。裂纹尖端主要承受层间剥离、层间剪切以及层内剪切作用。

Mode Ⅲ是三角填充区内部的随机裂纹扩展，如图6(c)所示。由于三角区内部没有纤维桥联，裂纹扩展的方向具有一定的随机性，但大致方向与裂纹上端结构所受弯矩的方向垂直，此时裂纹尖端主要为纤维与基体的剥离作用和基体的拉伸作用。

Mode Ⅳ是Mode Ⅰ和Mode Ⅱ的混合模式，即L型筋条与三角填充区的层间界面和筋条内部的子层界面先后发生分层失效。实验观测到弯曲失效模式的典型破坏形貌如图7所示。

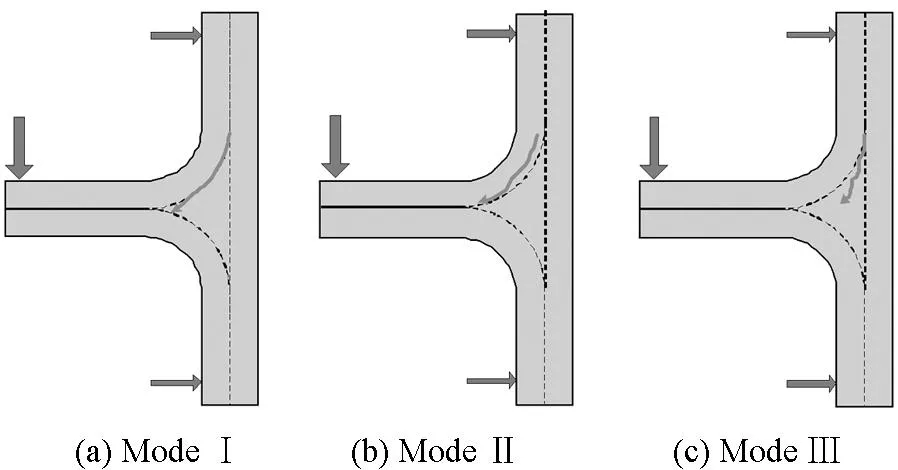
图6　弯曲加载下T型接头可能的失效模式Fig.6　Proposed failure modes of T-joints under bending load

图7　弯曲加载下观察到的T型接头的失效模式Fig.7　Observed failure modes of T-joints under bending load

3结论

1)通过基于黏聚区模型和蔡-吴失效准则的有限元分析，确定了在弯曲载荷的作用下，T型接头的失效关键部位为三角填充区及其相邻的L型筋条倒角圆弧段；分层失效由三角区上方与L型筋条的层间界面引发，并沿着倒角圆弧段界面扩展，同时可能伴有L型筋条子层内部或三角区的面内纤维或基体失效。

2)提出了T型接头在弯曲加载下的四种失效模式，分别由L型筋条与三角区的层间界面的脱黏失效、L型筋条子层内部的分层失效、三角填充区内部的随机裂纹扩展及前两者混合作用所主导的失效模式。

参考文献(References)

[1]Pei J H. Examination of key aspects defining the performance characteristics of out-of[J]. Composites Part A： Applied Science and Manufacturing, 1996, 27(2): 89-103.

[2]Shenoi R A, Read P J C L, Hawkins G L. Fatigue failure mechanisms in fibre-reinforced plastic laminated tee joints[J]. International Journal of Fatigue, 1995, 17(6): 415-426.

[3]Dodkins A R, Shenoi R A, Hawkins G L. Design of joints and attachments in FRP ships′ structures[J]. Marine Structures, 1994, 7(2): 365-398.

[4]Shenoi R A, Hawkins G L. Influence of material and geometry variations on the behaviour of bonded tee connections in FRP ships[J]. Composites, 1992, 23(5): 335-345.

[5]Phillips H J, Shenoi R A. Damage tolerance of laminated tee joints in FRP structures[J]. Composites Part A: Applied Science and Manufacturing, 1998, 29(4): 465-478.

[6]Orifici A C, Shah S A, Herszberg I, et al. Failure analysis in postbuckled composite T-sections[J]. Composite Structures, 2008, 86(1-3): 146-153.

[7]Stickler P B, Ramulu M. Experimental study of composite T-joints under tensile and shear loading[J]. Advanced Composite Materials, 2006, 15(2): 193-210.

[8]Stickler P B, Ramulu M. Investigation of mechanical behavior of transverse stitched T-joints with PR520 resin in flexure and tension[J]. Composite Structures, 2001, 52(3-4): 307-314.

[9]Stickler P B, Ramulu M, Johnson P S. Experimental and numerical analysis of transverse stitched T-joints in bending[J]. Composite Structures, 2000, 50(1): 17-27.

[10]Koh T M, Isa M D, Feih S, et al. Experimental assessment of the damage tolerance of Z-pinned T-stiffened composite panels[J]. Composite Part B:Engineering, 2013, 44(1): 620-627.

[11]Koh T M, Feih S, Mouritz A P. Strengthening mechanics of thin and thick composite T-joints reinforced with Z-pins[J]. Composite Part A:Applied Science and Manufacturing, 2012, 43(8): 1308-1317.

[12]Koh T M, Feih S, Mouritz A P. Experimental determination of the structural properties and strengthening mechanisms of z-pinned composite T-joints[J]. Composite Structures, 2011, 93(9): 2222-2230.

[13]Park Y B, Lee B H, Kweon J H, et al. The strength of composite bonded T-joints transversely reinforced by carbon pins[J]. Composite Structures, 2012, 94(2): 625-634.

[14]Burns L A, Mouritz A P, Pook D, et al. Bio-inspired design of aerospace composite joints for improved damage tolerance[J]. Composite Structures, 2012, 94(3): 995-1004.

[15]Burns L A, Mouritz A P, Pook D, et al. Strength improvement to composite T-joints under bending through bio-inspired design[J]. Composite Part A:Applied Science and Manufacturing, 2012, 43(11): 1971-1980.

[16]Engelstad S P, Berry O T, Renieri G D, et al. High fidelity composite bonded joint analysis validation study-part I: analysis[C]//Proceedings of 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference,AIAA, 2005.

[17]Engelstad S P, Mollenhauer D H, Berry O T, et al. Comparisons of measured moire fringe surface strains and model predictions for a co-bonded pi-preform composite tee joint[C]//Proceedings of 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference,AIAA, 2004.

[18]Engelstad S P, Berry O T, Averill R C, et al. Implementation and application of zig-zag finite elements for composite bonded tee-joint modeling[C]//Proceedings of 19th AIAA Applied Aerodynamics Conference ,AIAA, 2001.

[19]Wagner W, Balzani C. Simulation of delamination in stringer stiffened fiber-reinforced composite shells[J]. Computers & Structures, 2008, 86(9): 930-939.

[20]白江波, 熊峻江, 程序, 等. RTM 成型复合材料 T 型接头工艺参数优化与力学性能实验研究[J]. 复合材料学报, 2009, 26(3): 13-14.

BAI Jiangbo, XIONG Junjiang, CHENG Xu, et al. Processing parameter optimization and experimental investigation on mechanical properties for RTM composite T-joint[J]. Acta Materiae Compositae Sinica, 2009, 26(3): 13-14.(in Chinese)

[21]罗楚养, 熊峻江, 程泽林, 等. 复合材料 RTM 十字型接头疲劳性能对比实验研究[J]. 材料工程, 2009(1): 74-76.

LUO Chuyang, XIONG Junjiang, CHENG Zelin, et al. Experimental investigation on fatigue behaviour of RTM composite cross-joints[J]. Journal of Materials engineering, 2009(1): 74-76.(in Chinese)

[22]王雪明, 谢富原, 李敏, 等. 热压罐成型加筋板 L 形筋条纤维密实影响因素研究[J]. 航空材料学报, 2011, 31(4): 64-68.

WANG Xueming, XIE Fuyuan, LI Min, et al. Experimental research on fiber composite of L-shaped stiffeners in stiffened skins by autoclave process[J]. Journal of Aeronautical Materials, 2011, 31(4): 64-68.(in Chinese)

[23]谢富原, 王雪明, 李敏, 等. T形加筋板热压罐成型过程压力分布与树脂流动实验研究[J]. 复合材料学报, 2009,26(6): 66-71.

XIE Fuyuan, WANG Xueming, LI Min, et al. Experimental research on pressure distribution and resin flow of T-stiffened skins in autoclave process[J]. Acta Materiae Compositae Sinica, 2009,26(6): 66-71.(in Chinese)

[24]崔浩, 李玉龙, 刘元镛, 等. 基于粘聚区模型的含填充区复合材料接头失效数值模拟[J]. 复合材料学报, 2010, 27(2): 161-168.

CUI Hao, LI Yulong, LIU Yuanyong, et al. Numerical simulation of composites joints failure based on cohesive zone model[J]. Acta Materiae Compositae Sinica, 2010, 27(2): 161-168.(in Chinese)

[25]De Borst R. Numerical aspects of cohesive-zone models[J]. Engineering Fracture Mechanics, 2003, 70(14): 1743-1757.

[26]寇剑锋, 徐绯, 郭家平, 等. 黏聚力模型破坏准则及其参数选取[J]. 机械强度, 2011, 33(5): 714-718.

KOU Jianfeng, XU Fei, GUO Jiaping, et al. Damage laws of cohesive zone model and selection of the parameters[J]. Journal of Mechanical Strength, 2011, 33(5): 714-718.(in Chinese)

[27]朱亮, 崔浩, 李玉龙, 等. 含缺陷复合材料 T 型接头失效数值分析[J]. 航空学报, 2012, 33(2): 287-296.

ZHU Liang, CUI Hao, LI Yulong, et al. Numerical simulation of the failure of composites T-joints with defects[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(2): 287-296.(in Chinese)

[28]Harper P W, Hallett S R. Cohesive zone length in numerical simulations of composite delamination[J]. Engineering Fracture Mechanics, 2008, 75(16): 4774-4792.

Failure analysis of composite T-joints under bending load

WUHai,XIAOJiayu,XINGSuli,WENSiwei,YANGFubiao,YANGJinshui

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：A finite element model of the composite T-joints under bending load was established. The Tsai-Wu failure criterion and a cohesive zone model were used to simulate and analyze the failure mechanisms and carrying capacities of the composite T-joints under bending load. By static bending experiments, four failure modes have been investigated during bending failure processes of the composite T-joints. The maximum bending load of the T-joint calculated by finite element model methods was consistent well with experimental results.

Key words：T-joints; Tsai-Wu failure criterion; surface-based cohesive behavior; failure modes; bending failures

中图分类号：TB332

文献标志码：A

文章编号：1001-2486(2016)01-056-07

作者简介：吴海(1986—)，男，安徽安庆人，博士研究生，E-mail：hongwugong86@163.com；肖加余(通信作者)，男，教授，博士，博士生导师，E-mail：Jiayuxiao@tom.com

基金项目：湖南省重大科技专项资助项目(2011FJ1001)

*收稿日期：2015-03-16

doi:10.11887/j.cn.201601010

http://journal.nudt.edu.cn