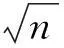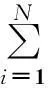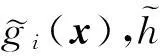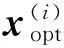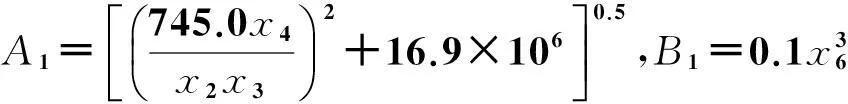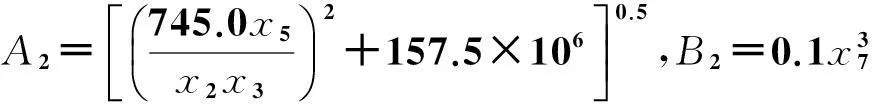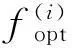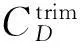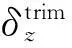序列近似优化方法及其在火箭外形快速设计中的应用*

彭　科，胡　凡，张为华，武泽平

(国防科技大学 航天科学与工程学院, 湖南 长沙　410073)



序列近似优化方法及其在火箭外形快速设计中的应用*

彭科，胡凡，张为华，武泽平

(国防科技大学 航天科学与工程学院, 湖南 长沙410073)

摘要：针对序列近似优化方法在代理模型构造与采样策略等方面的不足，基于采样点局部密度，引入与局部密度成反比的样本点影响体积概念，通过优化总影响体积确定径向基函数最优核宽度，满足序列近似优化过程不同规模、非均匀样本条件下的函数近似需要；建立潜在可行域最大距离加点准则，并与潜在最优加点准则结合平衡算法的探索能力与开发能力；建立三步收敛判定准则；构建改进序列近似优化的算法流程。对于Golinski减速器的优化设计问题，算法在目标函数调用42次后便搜索到全局最优解，体现了其良好的全局寻优能力与搜索效率。以“天航二号”火箭为例，建立其外形优化问题数学模型，所提优化方法在调用原始计算模型165次之后便搜索到全局最优解，大大提高了设计效率，同时飞行试验也表明设计结果满足要求。

关键词：序列近似优化；代理模型；采样策略；局部密度；收敛判定准则；“天航二号”火箭；外形优化

序列近似优化(Sequential Approximate Optimization，SAO)方法基于少量初始采样点构造初始代理模型，采取一定的加点策略更新采样点，逐步提高代理模型对最优解的近似精度，根据收敛准则终止算法并输出最优解[1-4]。相比智能优化算法，序列近似优化方法可在保证全局最优的前提下大幅降低原模型调用次数，显著提高优化效率[1]。代理模型构造与采样策略是序列近似优化方法的两项关键技术，国内外学者对此进行了大量研究[3-7]。

径向基插值模型在精度和鲁棒性方面皆较为可靠[8]，是序列近似优化方法中被广泛使用的代理模型，其核宽度的合理确定对近似精度有决定性影响。文献[6]解决了采样点较为均匀条件下的径向基函数核宽度确定问题；文献[4]提出了一种采样点个数趋于无穷情况下的非均匀核宽度确定方法；文献[1]提出了基于采样点局部密度的核宽度确定方法，但算法中总影响体积这一关键参数依赖经验确定，难以实现最优的近似精度。序列近似优化过程中样本点数量由少逐渐增多，样本分布较不均匀，建立不同规模、非均匀样本的径向基函数(Radial Basis Function, RBF)核宽度确定方法，对提高序列近似优化过程代理模型精度、提高优化效率具有重要意义。

合理的加点策略是平衡算法探索能力与开发能力以保证全局最优前提下提高算法收敛速率的关键因素，目前常用的再采样策略主要有：EI准则[9]、潜在最优加点准则、最大曲率准则、最小密度加点准则等，现有准则各有特点，但皆难以同时保证优化结果的全局性与收敛速率。

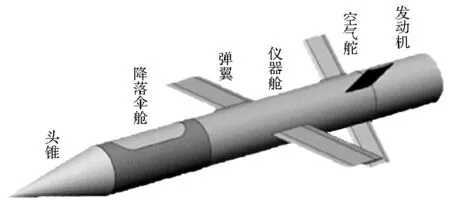
火箭外形设计问题是总体设计过程的重要问题，不断提高外形设计效率是设计人员的不懈追求。本研究基于样本点局部密度，引入与局部密度成反比的样本点影响体积概念，通过优化总影响体积确定径向基函数最优核宽度，并验证近似效果；建立潜在可行域最大距离加点准则并与潜在最优加点准则结合，平衡序列近似优化过程的收敛速度与全局搜索精度；建立收敛判定准则；构建改进序列近似优化的算法流程并通过算例分析算法性能；以“天航二号”(TianHang-Ⅱ, TH-Ⅱ)火箭为例，建立其外形优化问题数学模型，采用序列近似优化方法求解并分析结果。

1径向基函数最优核宽度确定方法

基本径向基函数的数学模型为：

(1)

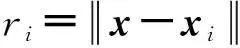
取基函数为Gauss函数，即：

(2)

式中，σi为基函数的核宽度。

基本径向基函数模型是一种非线性代理模型，对线性模型预测误差较大，故将线性项引入径向基代理模型，可以增加其线性泛化能力。其数学模型为：

(3)

式中，n为设计空间维数，λj(j=0,1,2,…,n)为线性回归系数。

式(3)中前两项为样本点的线性回归模型：

(4)

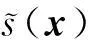
(5)

此时将N个训练样本代入式(5)，求解线性方程组即可求得基函数的权系数wi(i=1,2,…,N)。

下面选取线性模型

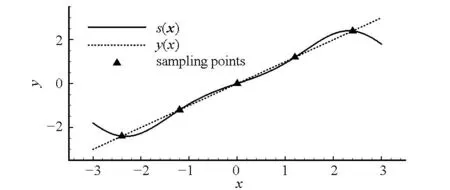
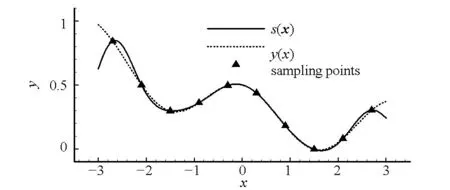
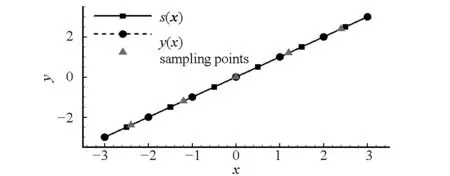
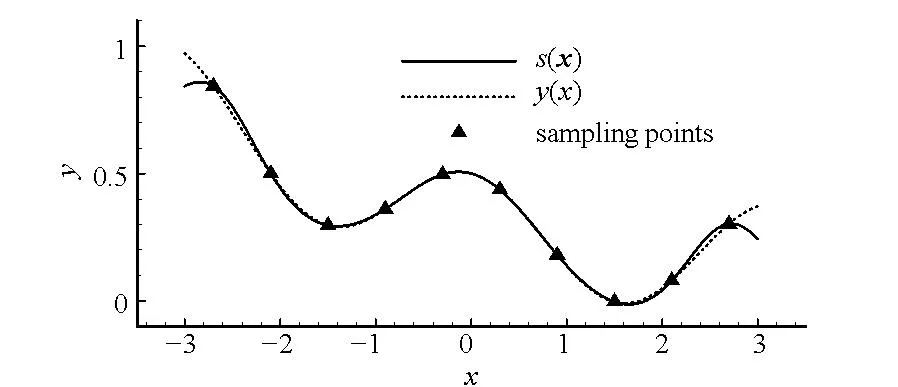
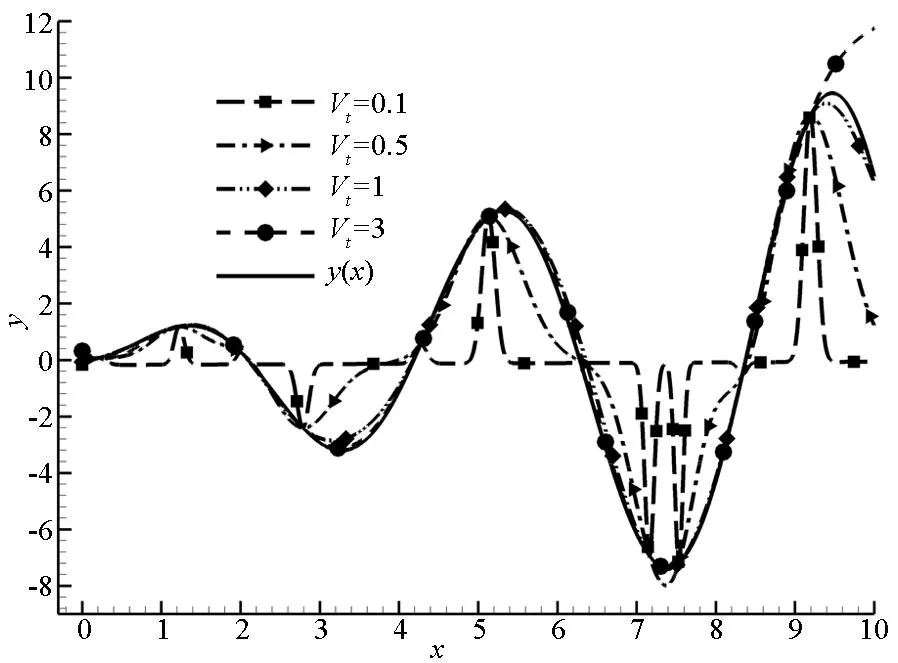
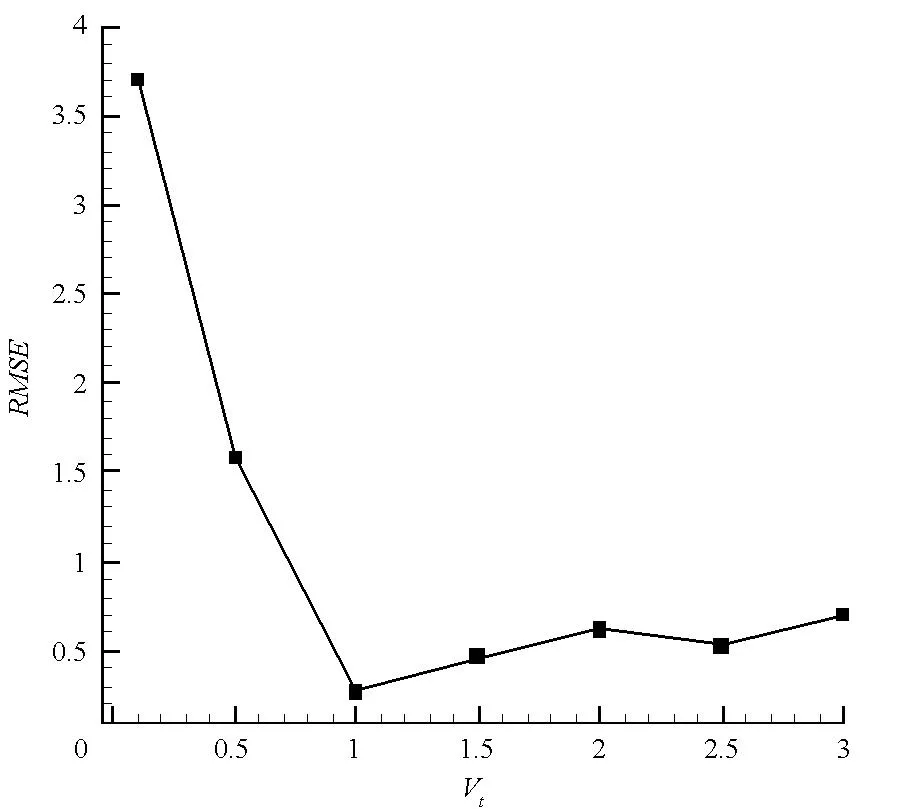
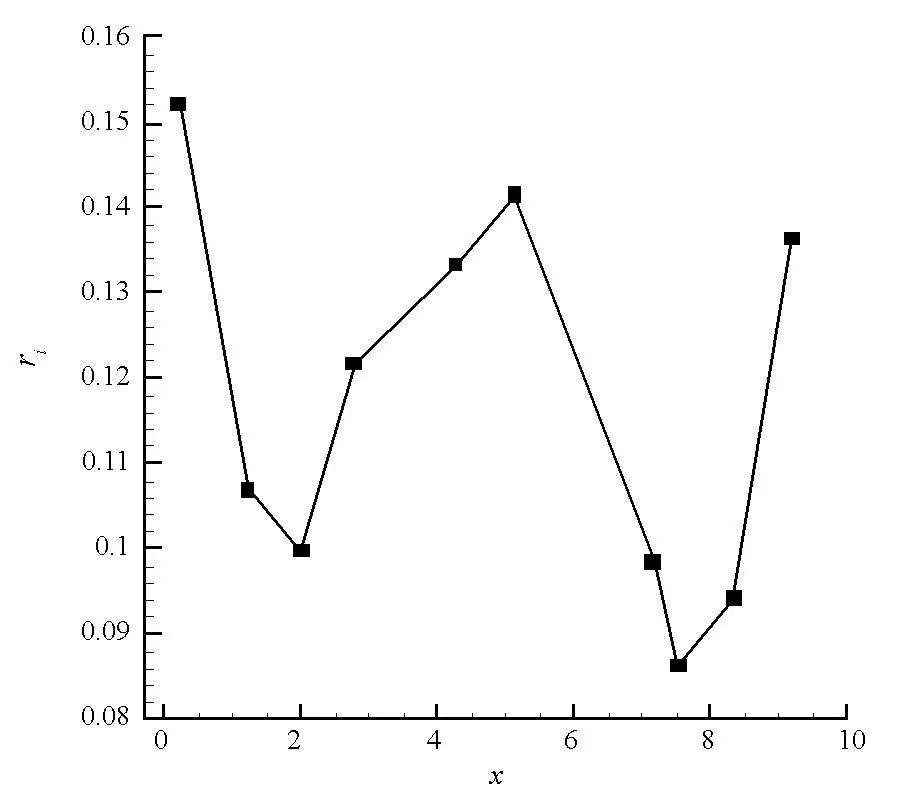
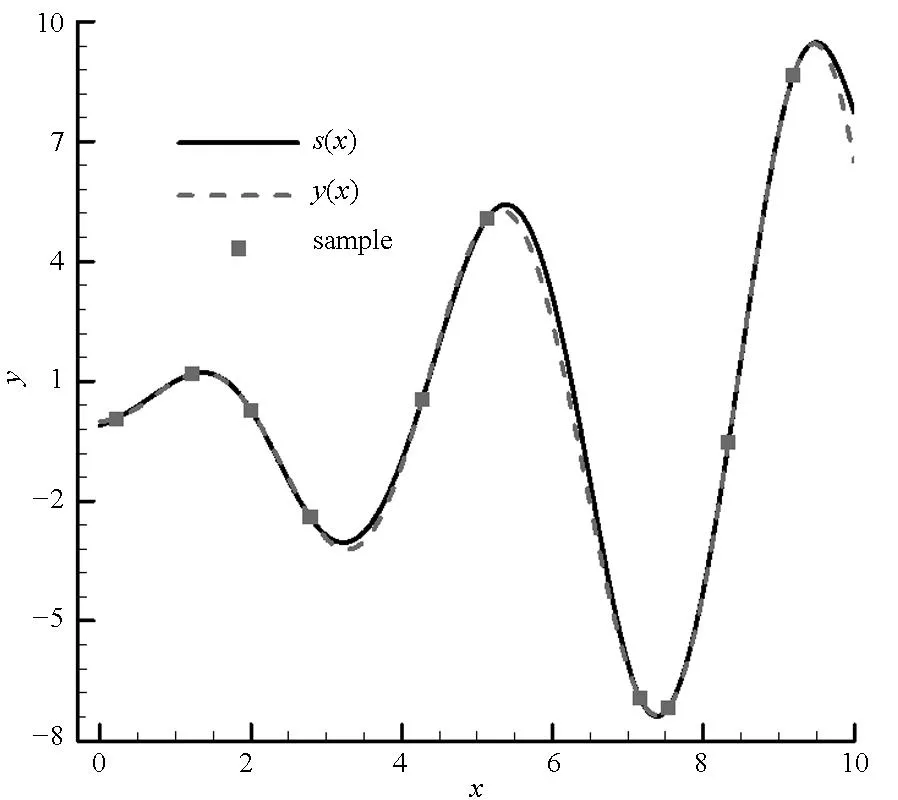
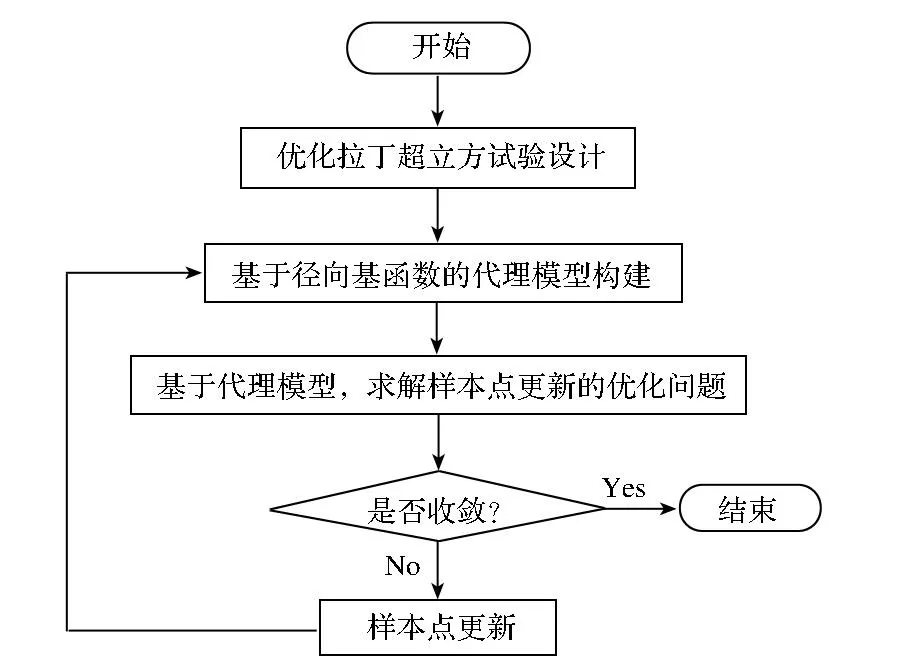
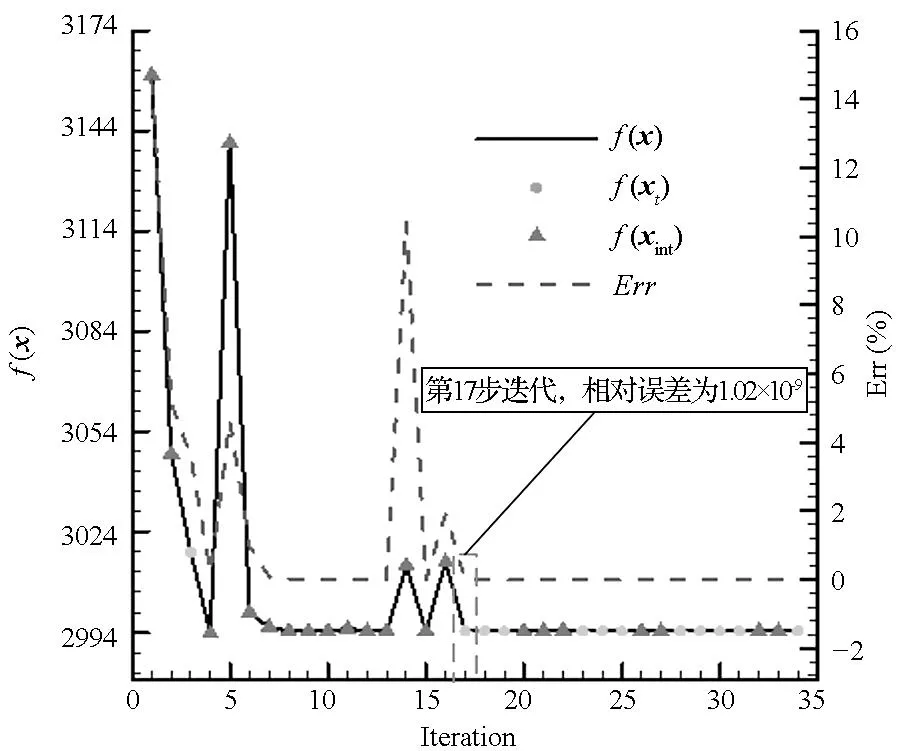
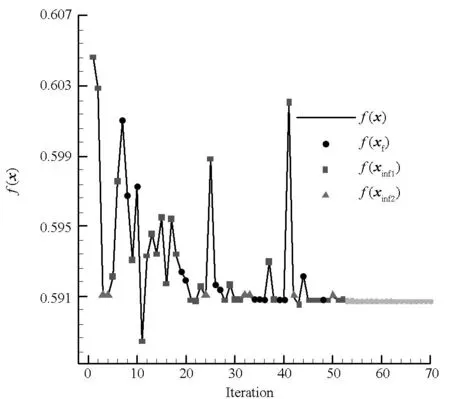
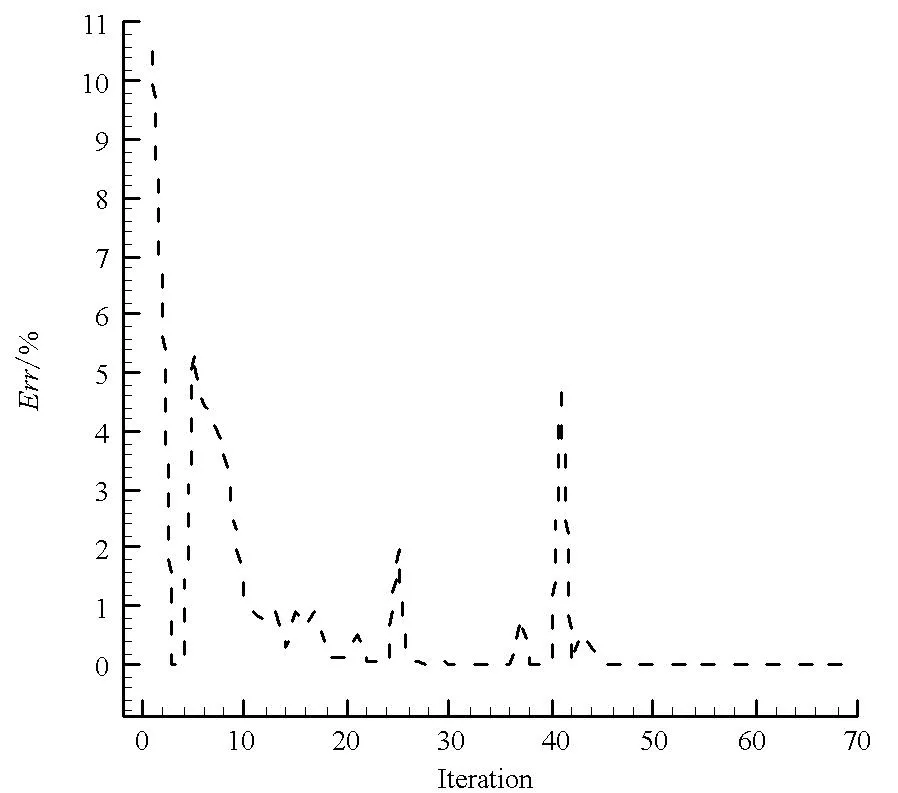
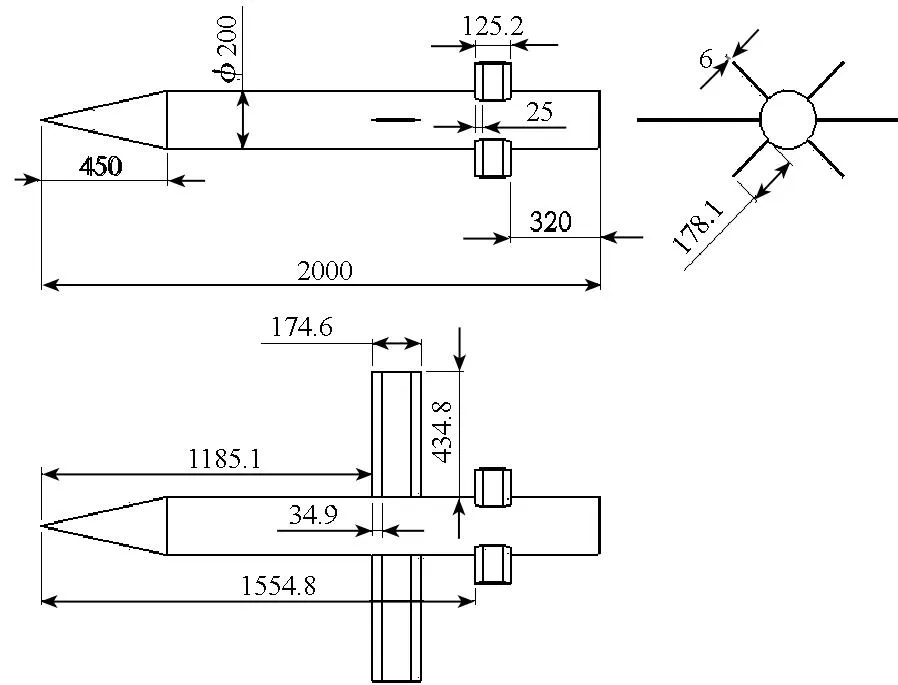
y=x,-3

(6)

与非线性模型

(7)

对基本径向基函数与含线性项径向基函数的近似能力进行比较，结果如图1、图2所示，后者对线性函数的近似能力显著高于前者，对非线性函数的近似能力也略优于前者，体现了其很好的线性和非线性泛化能力。

(a) 线性函数(a) Linear function

(b) 非线性函数(b) Nonlinear function图1　基本径向基函数对测试函数的近似Fig.1　Elementary RBF for testing function approximation

式(2)中基函数的核宽度σi对代理模型预测精度有决定性影响，文献[1]提出了基于样本点局部密度的核宽度σi计算方法，局部密度定义如式(8)所示。

(a) 线性函数(a) Linear function

(b) 非线性函数(b) Nonlinear function图2　含线性项径向基函数对测试函数的近似Fig.2　RBF containing linear terms for testing function approximation

(8)

(9)

(10)

在样本点分布较密的区域应使每个样本点的影响适当减小，即核宽度σi应相对较小，而在样本点分布较为稀疏区域应取相对较大的核宽度σi。 算法步骤如下[1]：

1)根据式(8)计算每个样本点的密度ρ(xi)；

2)按Vi/Vj=ρj/ρi计算每个样本点的影响体积之比；

Vt为所有样本点的影响体积总和，其取值直接决定各样本点对应核宽度，从而对径向基代理模型精度产生影响，文献[1]中Vt取值根据经验给出。图3以函数f(x)=xsin(1.5x)为例，给出了10个随机采样点情况下不同Vt值对应代理模型与原函数的对比情况；代理模型均方根误差(Root Mean Square Error, RMSE)随Vt变化规律如图4所示。由图可知，当Vt过小或过大皆不能实现较好的近似效果，确定最优Vt即可得到径向基函数最优核宽度，对提高代理模型精度具有关键意义。

图3　不同Vt值对应代理模型与原函数的对比Fig.3　Comparison between surrogate models applying different Vtvalues and original model

图4　不同Vt值对应代理模型均方根误差Fig.4　RMSE of different Vt

最优Vt值与样本在设计空间的分布有关，对样本数量不敏感[1]。将样本点均分为分区情况基本一致的两份分别作为近似建模样本与验证样本，以验证样本点代理模型预测值均方根误差最小为目标，采用黄金分割法[10]迭代搜索最优Vt。 近似建模样本各点局部密度ρ(xi)确定后，黄金分割法搜索最优Vt的单步计算过程如下：

1)根据Vt值计算近似建模样本点的核宽度ri；

2)求解式(3)中λj与wi得代理模型s(x)；

3)根据代理模型s(x)计算验证样本点预测值；

4)验证样本点计算预测值均方根误差。

采用以上方法得图3对应样本点最优Vt值为1.17，对应核宽度如图5所示，代理模型与原函数的对比如图6所示，二者均方根误差为0.25，吻合较好，表明给出的径向基函数最优核宽度确定方法有效。

图5　最优样本点核宽度Fig.5　Optimized kernel width of each sampling points

图6　最优Vt值对应代理模型与原函数的对比Fig.6　Comparison between surrogate model applying optimized Vt and original model

2改进序列近似优化方法

2.1序列近似优化方法基本流程

文献[1]建立了如图7所示的序列近似优化方法基本流程，主要步骤为：①将设计空间线性映射到n维单位立方体内，采用拉丁超立方方法得到初始采样点，并计算采样点目标函数与约束值；②基于径向基函数构建目标函数与各约束值的代理模型；③基于代理模型，求解样本点更新的优化问题；④收敛判断。

图7　序列近似优化方法基本流程Fig.7　Flow chart of sequential approximate optimization

2.2采样点更新准则

一般优化问题可表述为如式(11)所示形式：

(11)

式中，i=0表示无不等式约束，j=0表示无等式约束。

最大距离加点准则是序列近似优化过程常用的加点准则，可最大程度保证算法的探索能力。

令求解域中点x到所有样本点的最小距离dmin(x)为：

(12)

(13)

为平衡算法的探索能力与开发能力，兼顾序列近似优化过程的收敛速度与全局搜索精度，将潜在最优加点准则与潜在可行域最大距离加点准则同时使用。潜在最优加点将式(14)的最优解作为新的样本点加入到模型中。

(14)

采样点更新涉及式(13)、式(14)定义的两个优化问题，皆采用粒子群优化算法求解。

2.3收敛判定准则

按以下3个步骤判断算法是否收敛：

(15)

式中，i=N-Sxl+1,N-Sxl+2,…,N-1。

(16)

以上三步皆满足时则近似序列优化收敛。

改进后的序列近似优化方法流程图如图8所示。

图8　改进序列近似优化算法流程图Fig.8　Flow chart of enhanced sequential approximate optimization

2.4算例分析

Golinski减速器优化设计问题是美国国家航空航天局提供的一个多学科设计优化测试问题[11]，其目标函数为重量最小，共有7个设计变量：齿轮面宽度x1、牙膜x2、小齿轮牙齿数目x3、轴1长度x4、轴2长度x5以及轴1与轴2的直径x6和x7。其数学模型表述如式(17)所示。

(17)

式中：

各设计变量取值方位如表1所示。

表1　Golinski减速器设计变量取值范围

注：圆点为可行解；三角形为不可行解。图9　Golinski减速器优化问题目标函数与误差收敛曲线Fig.9　Convergence curve of objective function and relative error for Golinski retarder optimization

所用方法在迭代至第4步，目标函数调用15次之后便搜索到全局最优解附近；迭代至17步，目标函数调用42次后搜索到全局最优解：x=[3.5,0.7,17,7.3,7.715 3,3.350 2,5.286 7]T；代理模型函数值与真实模型函数值的相对误差仅为1.02×10-9。文献[12]提出的并行模拟退火单纯形算法是目前搜索效率相对很高的智能优化算法，该方法搜索到Golinski减速器优化问题最优解附近约需调用1000次原始模型。本文方法能在保证全局搜索精度的前提下显著减少模型调用次数，可大幅提高火箭外形设计优化问题求解效率。

3“天航二号”火箭外形快速设计优化

3.1优化问题

根据总体要求与任务特点，“天航二号”火箭气动布局为“—·×”布局，总长为2000 mm，头部长度为450 mm，发动机长度取为320 mm，弹翼、空气舵皆为矩形，空气舵紧贴仪器舱后端面安装，如图10所示。“天航二号”满载质量为60 kg，对应质心系数0.56，耗尽质量为56 kg，对应质心系数为0.53。

图10　“天航二号”火箭外形布局Fig.10　 TH-Ⅱ rocket configuration

1)设计变量为：翼距头部距离、翼弦长、翼展长、舵弦长、舵展长，取值范围依次为[1000, 1250]、[150, 190]、[350, 500]、[100, 150]、[150, 200](单位mm)。

综上，“天航二号”火箭外形优化问题数学模型为：

(18)

式中，g4(x)为几何约束。

3.2优化结果与分析

优化过程气动特性计算采用工程方法[13]完成，取初始样本点为100个，迭代至第33步，原始计算模型调用165次之后便搜索到全局最优解，所用机时仅为190.6 s(AMD Athlon 四核处理器，主频2.8 GHz)，大大提高了设计效率。优化过程目标函数收敛曲线如图11所示，相对误差收敛曲线如图12所示，外形优化结果如图13所示。需要说明的是，式(18)中约束条件与目标函数计算分三步，依次为：先g1(x)和g2(x)，然后g3(x)和g4(x)，最后f(x)，图11中三角形对应样本点因其g2(x)值不满足约束，无须计算目标函数f(x)值，f(x)为人为给定值。

注：圆点为可行解；三角形与方行为不可行解。图11　火箭外形优化目标函数收敛曲线Fig.11　Convergence curve of objective function for rocket shape optimization

图12　火箭外形优化相对误差收敛曲线Fig.12　Convergence curve of relative error for rocket shape optimization

图13　“天航二号”火箭外形优化结果Fig.13　TH-II rocket optimized shape

图14为采用本软件系统设计优化气动外形得到的“天航二号”火箭飞行试验概况，飞行试验取得圆满成功，表明本文设计优化得到的“天航二号”试验火箭静稳定性、操纵性、配平升阻力特性等性能指标符合设计要求，满足工程需要。

4结论

研究改进了序列近似优化方法，并将其应用于火箭快速设计，主要研究工作和结论如下：

(a) 总装后外形(a) Shape after assembling

(b) 点火出架(b) Firing　　(c) 开伞回收(c) Recovery using parachute图14　“天航二号”火箭飞行试验概况Fig.14　TH-Ⅱ rocket flight test

1)建立了含线性项的径向基函数，提高了其对线性函数的近似能力；基于样本点的局部密度，采用黄金分割法得到了最优总影响体积数值，进而计算最优核宽度，仿真结果表明了该方法的有效性。

2)建立了潜在可行域最大距离加点准则并与潜在最优加点准则结合，兼顾了序列近似优化算法的探索能力与开发能力；提出了序列近似优化方法三步收敛判定准则；构建了改进序列近似优化的算法流程；通过Golinski减速器优化设计问题分析了算法性能，目标函数调用42次后便搜索到全局最优解，体现了良好的全局寻优能力与搜索效率。

3)以“天航二号”火箭为例，建立了其外形优化问题数学模型，采用改进的序列近似优化方法迭代至第33步，原始计算模型调用165次之后便搜索到全局最优解，所用机时仅为190.6 s，大大提高了设计效率。“天航二号”火箭飞行试验取得圆满成功，表明设计优化得到的“天航二号”试验火箭各项气动性能指标符合设计要求，满足工程需要。

参考文献(References)

[1]Wang D H, Wu Z P, Fei Y, et al. Structural design employing a sequential approximation optimization approach[J]. Computers and Structures, 2014, 134:75-87.

[2]Kitayama S, Arakawa M, Yamazaki K. Sequential approximate optimization for discrete design variable problems using radial basis function network[J]. Applied Mathematics and Computation, 2012, 219(8): 4143-4156.

[3]Nakayama H, Arakawa M, Sasaki R. Simulation-based optimization using computational intelligence[J]. Optimization and Engineering, 2002, 3(2): 201-214.

[4]Kitayama S, Arakawa M, Yamazaki K. Sequential approximate optimization using radial basis function network for engineering optimization[J]. Optimization and Engineering, 2011, 12(4): 535-557.

[5]Deng Y M, Lam I C, Tor S B, et al. A CAD-CAE integrated injection molding design system [J].Engineering with Computers, 2002, 18: 80-92.

[6]Kitayama S, Yamazaki K. Simple estimate of the width in Gaussian kernel with adaptive scaling technique[J]. Applied Soft Computing, 2011, 11(8): 4726-4737.

[7]Luo C T, Zhang S L, Wang C, et al. A metamodel-assisted evolutionary algorithm for expensive optimization[J]. Journal of Computational and Applied Mathematics, 2011, 236(5): 759-764.

[8]Jin R, Chen W, Simpson T W. Comparative studies of metamodeling techniques under multiple modeling criteria[J]. Journal of Structural and Multidisciplinary Optimization, 2001, 23(1): 1-13.

[9]Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21: 345-383.

[10]谢政， 李建平， 陈挚. 非线性最优化理论与方法[M]. 北京: 高等教育出版社, 2010.

XIE Zheng, LI Jianping, CHEN Zhi. Nonlinear optimization theory and methods[M]. Beijing: Higher Education Press, 2010. (in Chinese)

[11]Padula S L, Alexandrov N, Green L L. MDO test suite at NASA langley research center[C]//Proceedings of 6th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Bellevue, 1996.

[12]Luo Y Z,Tang G J. Parallel simulated annealing using simplex method [J].AIAA Journal, 2006, 44(12): 3143-3146.

[13]严恒元. 飞行器气动特性分析与工程计算[M]. 西安: 西北工业大学出版社, 1990.

YAN Hengyuan. Aircraft aerodynamic characteristics analysis and engineering calculation[M]. Xi′an: Northwestern Polytechnic University Press, 1990. (in Chinese)

Sequential approximate optimization method and its application in rapid design of rocket shape

PENGKe,HUFan,ZHANGWeihua,WUZeping

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：Sequential approximate optimization method has shortcomings in several respects, such as surrogate model establishing and infill strategy at present. Basing on local density of sampling points, the influence volume concept which is inversely proportional to local density was introduced and then the optimal kernel width of radial basis function was obtained by means of total influence volume optimization, thus, the function approximation needs in sequential approximate optimization process under the conditions of different scales and heterogeneous samples were satisfied. Potential feasible region infill strategy was proposed and potential optimal strategy was applied together, both exploration and exploitation capacity of the algorithm were satisfied. Three-step convergence criterion was set up. The algorithm flow process of sequential approximate optimization was constructed. For Golinski reducer optimization problem,the global optimal solution was solved after calculating original model 42 times, which embodied the good global optimization capacity and searching efficiency of the algorithm. Shape optimization mathematical model was established for TH-II rocket, global optimal shape was gained after 165 times of original model calling using the proposed method. The design efficiency was increased greatly and TH-II rocket aerodynamic shape was proved reliable by flight testing.

Key words：sequential approximate optimization; surrogate model; infill strategy; local density; convergence criterion; TH-II rocket; shape optimization

中图分类号：V421.1；TP391.7

文献标志码:A

文章编号：1001-2486(2016)01-129-08

作者简介：彭科(1989—)，男，四川邻水人，博士研究生，E-mail：pengke_pk@163.com；张为华(通信作者)，男，教授，博士，博士生导师，E-mail：zhangweihua@nudt.edu.cn

基金项目：国家自然科学基金资助项目(51105368)

*收稿日期：2015-02-03

doi:10.11887/j.cn.201601021

http://journal.nudt.edu.cn