变工况下轴承健康监测的相关向量机与自适应阈值模型方法*

胡　雷，范　彬，胡茑庆，高　明

(1.国防科技大学 机电工程与自动化学院， 湖南 长沙　410073；

2.国防科技大学 装备综合保障技术重点实验室， 湖南 长沙　410073)



变工况下轴承健康监测的相关向量机与自适应阈值模型方法*

胡雷1, 2，范彬1, 2，胡茑庆1, 2，高明1

(1.国防科技大学 机电工程与自动化学院， 湖南 长沙410073；

2.国防科技大学 装备综合保障技术重点实验室， 湖南 长沙410073)

摘要：工况在旋转机械运行过程中通常是变化的。变化的工况和故障一样，也会引起机械振动特征发生改变，从而引起诊断误差。为此，提出一种用于变工况下轴承健康监测的新方法。该方法使用相关向量机拟合振动特征的统计量随工况参数的变化，得到特征统计量与工况参数之间的连续函数关系；基于不同工况下的特征统计，构建自适应阈值模型。将该方法用于不同转速下的轴承健康监测，结果表明，当转速超过某一个较小的值时，该方法有效。

关键词：健康监测；相关向量机；自适应阈值；变工况；轴承

轴承故障是导致旋转机械失效的重要原因之一。针对轴承开展健康监测，及时发现轴承故障，支持维修决策，防止机械失效，对于保障旋转机械的使用安全性非常重要。传统的轴承健康监测方法基于这样的假设，即将轴承故障的响应视为滚动体通过损伤位置时引起的附加载荷。在转速固定时，附加载荷是一些周期性的响应激励。这些周期响应被称作是轴承的故障特征频率分量[1]。

然而不少旋转机械的运行工况是变化的。例如，飞机在慢车滑行、爬升、平飞、降落的过程中，发动机的转速和输出功率变化都很大。如果旋转机械在变化转速或者变化载荷的情况下工作，它的动力学和振动就会是非平稳的，即使是在机械健康的情况下，采集到的振动信号也是非平稳信号，信号的幅值和频率会随着时间改变。因此在变化的工况下，传统的用于平稳信号处理的频域处理方法就会失去作用。有大量的研究工作涉及健康监测和故障诊断的非平稳信号处理方法。这些方法包括短时傅里叶变换[2]、小波分析[3-4]、经验模式分解[5]、希尔伯特黄变换[6]、阶比跟踪[7]等。上述方法为变速条件下非平稳振动信号的分析提供了途径。这些方法和传统频域分析方法一样，都是用于振动信号的特征提取，而且所提取特征的幅值也是随健康状态变化而变化的。但是这些方法都没有考虑所提取的特征随运行工况变化的事实，没有考虑在转速、输出功率，特别是载荷变化的同时，正常地接触冲击能量和故障引起的冲击振动能量都会发生变化。考虑到故障，特别是早期故障引起的系统响应变化往往非常微弱，识别机械的振动响应变化是工况变化引起的还是故障状态引起的，就变得非常困难。

轴承的智能故障诊断可以通过模式识别方法实现。模式识别中的分类器模型，如神经网络、支持向量机和相关向量机等，被大量用于解决智能故障诊断问题[8-10]。分类器模型可以统一描述为y=f(x, a)，其中，y是样本所属的状态类别的标记，x是样本特征向量，a是分类器模型的参数。这些模型没有考虑工况变化的影响。以往用于健康监测的自适应检测模型，其基本思想是使用自适应训练方法，通过不断地更新训练样本集，重新训练检测模型[11-12]。这种思路一方面需要在线更新检测模型，因计算量的限制，不适合使用先进的模式识别方法；另一方面，这种思路只是通过更新训练样本集来更新模型，并没有在求解模型时考虑工况参数，因此会将缓变故障判断为工况变化的影响，不能有效识别缓变故障。

本文从模式识别方法的角度解决变工况下旋转机械中轴承的健康监测问题，提出一种基于相关向量机的自适应阈值检测模型，该模型的参数是运行工况的自适应函数。这些自适应函数由相关向量机回归拟合得到。由于自适应阈值模型的参数是工况参数的连续函数，因此该模型在所有运行条件下都可以使用。

1自适应高斯阈值检测模型

高斯阈值模型来源于切比雪夫不等式。对于一个服从高斯分布的特征x，假设其均值和标准差分别为m和d，则如下切比雪夫不等式成立：

(1)

该不等式意味着x(m-kd,m+kd)的概率大于1-k-2，k是阈值裕度。

根据切比雪夫不等式，当给定阈值裕度k，状态特征x的阈值区间可以构建为

C=[m-kd,m+kd]

(2)

由于只需考虑x的上界，因此可以构建决策函数为：

f(x)=m+kd-x

(3)

该式可以直接用于监测。具体地，f(x) ≥ 0意味着特征x正常；而f(x) < 0则意味着x异常。即使特征不服从高斯分布，只要阈值裕度选择合理，该模型同样适用。

由于变化的工况(为简化问题，这里仅考虑转速)同样会引起振动特征x发生变化，因此给振动特征x定义的决策函数将同时是特征x和转速s的函数。这里定义阈值模型的监测函数为

f(x,s)=m(s)+kd(s)-x

(4)

其中，m(s)和d(s)分别表示转速为s时，振动特征x的统计均值和标准差，m(s)+kd(s)是阈值。

为了让该阈值模型在任何转速下都可以使用，式(4)应该是转速s的连续函数，这一点只要m(s)和d(s)是连续函数就能得到保证。为此，本文使用两个相关向量机(Relevance Vector Machines, RVM)拟合m(s)和d(s)。其中，第一个在样本(s(n),m(n)(n= 1, 2, …,N))上训练，得到随转速变化的参数m(s)，s(n)和m(n)分别是第n个样本的转速和振动特征的统计均值，N是样本个数；第二个在(s(n),d(n))上训练，得到随转速变化的参数d(s)。d(n)是转速为s(n)时的振动特征的标准差。训练样本从健康轴承的测试信号中提取。

2相关向量机基本原理

相关向量机是支持向量机(Support Vector Machine, SVM)函数的概率稀疏核函数模型[13]。通过引入一个概率贝叶斯学习框架，RVM使用的基函数比SVM要少得多，而且具有比SVM更多的优势。这些优势包括概率模式的预测、参数的自动估计、可以使用任意的核函数等。

(5)

其中w=(w1…wN)T是权向量，k=[k(xi, x1) …k(xi, xN)]T核函数向量，w0是偏置。选择高斯核函数：

(6)

其中λ∞是核函数的宽度系数。

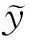
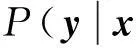
(7)

其中y=(y1…yN)，w=(w0…yN)，Φ是N×(N+1)矩阵，元素Φij=k(xi, xj-1)，Φi1=1。

为了避免过学习，RVM采用Bayesian思想，使用0均值高斯先验分布，对每个权值引入超参αi。从而权值的先验分布可以写为

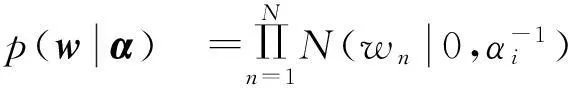
(8)

其中α=(α0…αN)。根据Bayes原理，权值的后验概率可以写为：

(9)

其中协方差矩阵Σ和期望μ分别为

Σ=(ΦTBΦ+A)-1

(10)

μ=ΣΦTΒy

(11)

其中A=diag(α0,α1, …,αN)，B=σ-2IN，IN为单位矩阵。

通过对权值积分，可以得到最大似然：

(12)

通过最大化似然函数计算超参α的后验分布，得到最大似然值。由于很多权值为0，只有很少的核函数被用于构建预测模型。这一特性叫稀疏性，可以得到稀疏模型，计算也快。具有非零权向量的{xi,yi}称作相关向量。

3基于RVM的自适应检测模型构建

为了构建并验证所提出的自适应检测模型的有效性，在实验环境下开展变工况下的轴承故障模拟实验，构建基于相关向量机的自适应检测模型。先后测试健康轴承、外环故障轴承和内环故障轴承的模拟试验，设置采样频率为25 000Hz，同步采集振动信号和转速信号。试验过程中，逐渐调节转速变化。

3.1训练数据准备

选择振动的均方根值(Root Mean Square, RMS)xR作为描述轴承健康状态的振动特征，xR的统计均值和标准差分别用mR和dR表示。RMS是振动信号能量水平的一个测度。由于故障发生时，振动能量水平通常会增加，因此RMS可以很好地用于旋转机械的故障诊断和预测[14-15]。

1)原始数据采集。调整健康轴承的转速，具体地，先升速到设定转速，然后再减速至停止转动。在操作过程中，同步采集振动信号vi和转速信号ri，下标i表示信号来源于第i次测试，i=1, 2, …,L。原始振动信号使用加速度传感器采集。原始转速信号使用光学编码器采集。vi和ri是所提方法的原始数据。

2)转速和振动水平的估计。使用光学编码器采集的原始转速信号ri是一系列的脉冲。旋转机械每转一周产生一个脉冲。在原始数据中寻找满足ri(j)≤0和ri(j+1)≥0的点，过零时间tj可以用线性插值估计

(13)

其中，t(j)和t(j+1)是ri(j)和ri(j+1)的时间。tj时刻的转速sj可以用式(14)估计

(14)

其中，tj是第j个过零点时间，tj-1是第(j-1)个过零点时间。在时间段(tj-1,tj]内估计振动信号的RMS，用以表示tj时刻的振动水平。

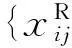
(15)

进行L次测试，可以得到L次测试的RMS序列，进而在这L个RMS序列上计算振动特征的统计均值和标准差：

(16)

3.2检测模型构建

为了在健康状态下计算振动RMS的均值序列{mR(n)}和标准差序列{dR(n)}，在正常轴承做20次测试。测试时，转速在200 ～ 1200 r/min内任意调整。测试过程中同步采集振动和转速信号。轴承每转一周计算一次振动RMS和转速。为了生成RVM的训练样本，需要生成统一的转速序列，并计算每次测试对应于该转速序列的均值序列{mR(n)}和标准差序列{dR(n)}。如果设置序列长度N=201，生成的转速序列为{s(n),n=1, 2, …,N}={200, 205, 210, …, 1200}。

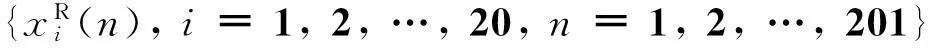
所提出的检测模型需要选择两个参数，式(4)中阈值裕度k和式(6)中核函数的宽度系数λ∞。核函数的宽度系数λ∞对RVM的性能起决定性的作用。λ∞越大，RVM越稀疏，相关向量越少。λ∞越小，相关向量越多，学习精度越高，推广性能越差。λ∞的选择是经验性的，交叉确认结果可以作为选择λ∞的参考。

为了交叉确认λ∞，定义训练误差E1和测试误差E2为

(17)

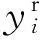
第一个用于拟合mR(s)的RVM，其交叉确认结果如图1所示。图1(a)是λ∞在[2, 58]区间内取值时，训练误差和测试误差的变化情况；从图中可以看出，刚开始训练误差和测试误差都随λ∞的增加急剧下降。当λ∞超过6之后，训练误差和测试误差又开始随着λ∞的增加而逐渐缓慢增加。图1(b)是相关向量个数；从图中可以看出，相关向量个数随λ∞增加而减少。从图1中可以发现，λ∞在[30, 60]范围内取值时，训练误差和测试误差都小于0.09，相关向量个数小于36，得到的模型稀疏性好。我们设置λ∞=48，在这种情况下，训练误差和测试误差都是0.05，相关向量个数是24。第二个用于拟合dR(s)的RVM，其交叉确认结果如图2所示。同样的可以从图2中发现，λ∞可以在[20, 58]区间内取值。当设置λ∞=28时，训练误差和测试误差都是0.06，相关向量个数为34。

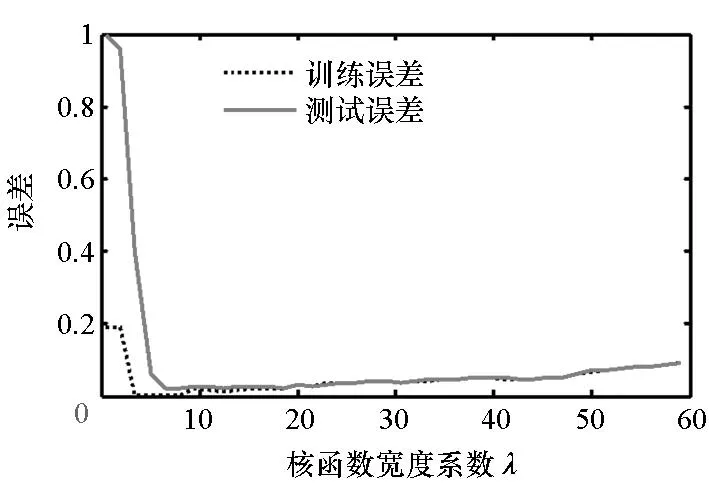
(a) 回归误差(a) Regression error

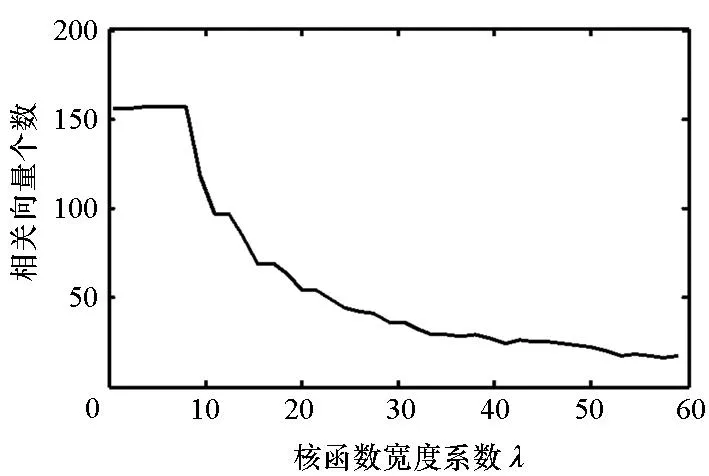
(b) 相关向量个数(b) Number of relevance vectors图1　RMS均值的回归精度和相关向量个数随核函数宽度系数的变化关系Fig.1　Regression error of mR and number of relevance vectors change with different kernel basis width

另一个需要设置的参数是阈值裕度k，k是用于平衡假正率和假负率的关键参数。根据式(4)，阈值裕度k越大，阈值区间就越大，正常样本超出阈值区间的概率就越小，意味着模型具有较小的假负率。反过来，阈值裕度k越小，阈值区间就越小，异常样本落入阈值区间的概率就越小，意味着模型具有较小的假正率。使用交叉确认方法选择阈值裕度k需要使用故障样本计算假正率。为了生成故障样本，开展轴承故障模拟试验，测试故障轴承振动信号。对于故障轴承，同样每转一周计算一次振动RMS和转速。

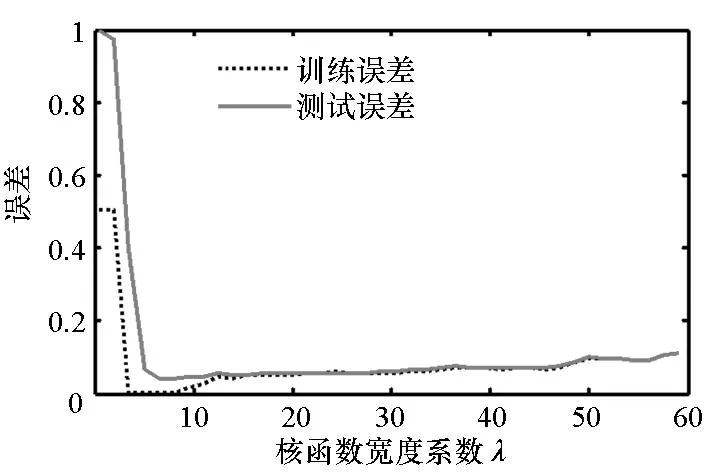
(a)回归误差(a) Regression error

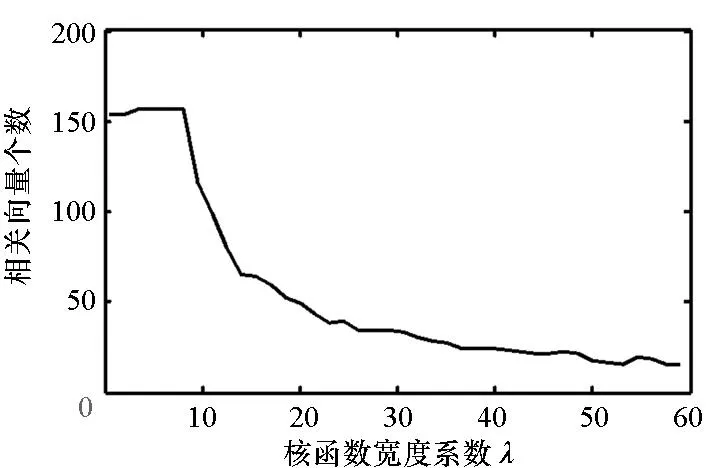
(b) 相关向量个数(b) Number of relevance vectors图2　RMS标准差的回归精度和相关向量个数随核函数宽度系数的变化关系Fig.2　Regression error of dR and number of relevance vectors change with different kernel basis width

设置阈值裕度的区间为[0.5, 10]，得到的监测结果的假正率和假负率如图3所示。可以看出，假负率随k的增加而减小，假正率随k的增加而增加。对于工程人员来说，假负率比假正率更难接受，因此选择一个较大的阈值裕度k=2.5。当设置k为3.5时，假负率接近0.01，假正率为0.23。

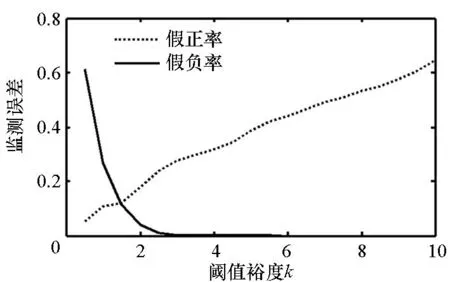
图3　测试误差随阈值裕度的变化Fig.3　Change of test error at different threshold margin

4试验验证结果分析与讨论

4.1轴承故障检测结果分析

图4所示是一次健康轴承测试数据的监测结果。在这次测试过程中，转速从200 r/min升到1200 r/min，提取的样本共2311个。从图4(a)中可以看出，共有11个样本的RMS超出了对应的阈值。这些样本的转速集中在[198 283] r/min区间内。这些健康轴承样本的健康指标是负值，如图4(b)所示，它们是假负样本，假负率为11/2311，约为0.48%。

(a)振动RMS和阈值(a) RMS and their thresholds

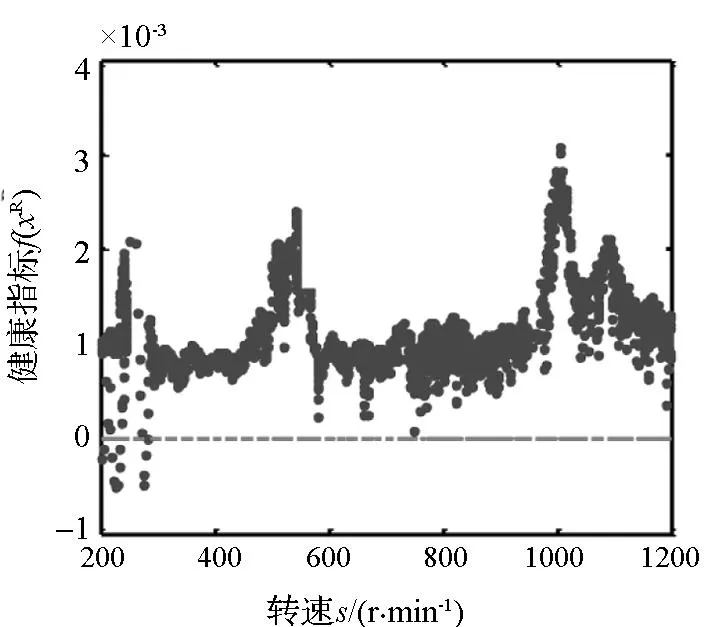
(b)健康指标与阈值(b) Health index and their thresholds图4　正常轴承健康监测结果Fig.4　Monitoring results of a healthy bearing

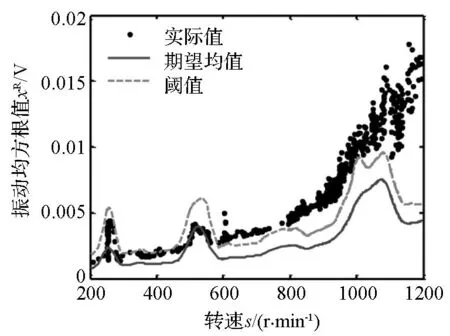
(a)振动RMS和阈值(a) RMS and their thresholds

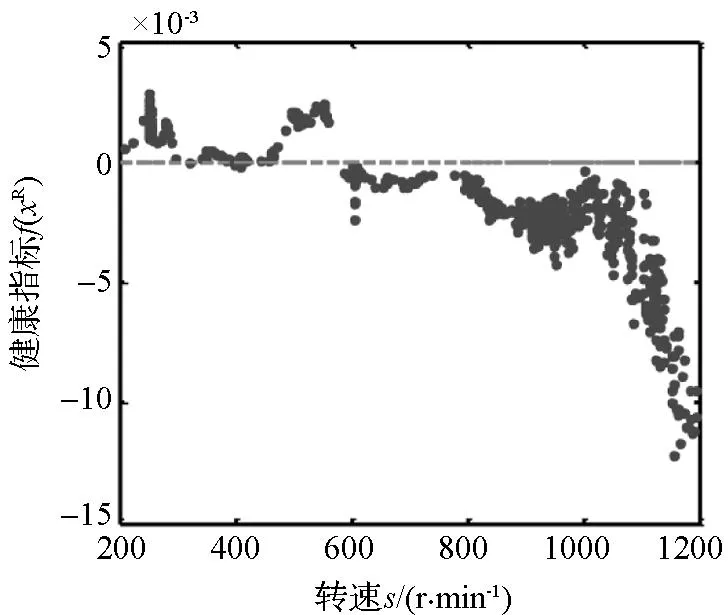
(b)健康指标与阈值(b) Health index and their thresholds图5　外环故障轴承的健康监测结果Fig.5　Monitoring results of a bearing with outer ring fault

图5所示为一个外环故障轴承的健康监测结果。从图中可以看出，在转速低于586 r/min的情况下，有大量样本的均方根值没有超出阈值，它们的健康指标为正，这些故障轴承的样本是假正样本。但是在转速高于586 r/min的情况下，测试样本的均方根值都大于阈值，对应的健康指标都是负值，指示出测试的轴承是故障轴承。

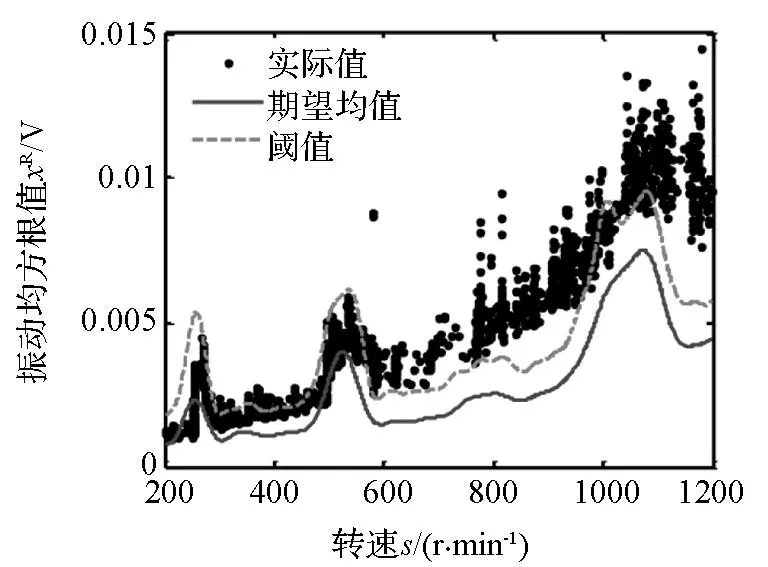
(a)振动RMS和阈值(a) RMS and their thresholds

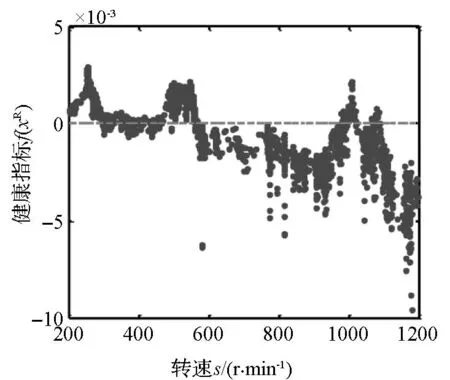
(b)健康指标与阈值(b) Health index and their thresholds图6　内环故障轴承的健康监测结果Fig.6　Monitoring results of a bearing with inner ring fault

图6所示为一个内环故障轴承的健康监测结果。从图中可以看出，在转速低于567 r/min的情况下，有大量样本的均方根值没有超出阈值，它们的健康指标为正，这些故障轴承的样本是假正样本。但是当转速超过567 r/min之后，均方根值没有超出阈值的样本，即假正样本，仅有51个。在转速区间[567 1200] r/min内，测试样本共1254个，因此假正率为51/1254，约为4.07%。

从上面的监测结果可以看出，本文提出的监测方法的假负率很小，假正率集中在低转速的情况。对其他测试的监测得到了类似的结果。由此可以得出结论，该方法在转速超过600 r/min之后有效。

4.2讨论

如前所述，滚动轴承故障响应可以看成是滚动体通过损伤区域时引起的附加载荷冲击。但是在低转速情况下，这些损伤引起的冲击载荷很小，而且从损伤位置传输到测点又被严重地削弱了。因此，本文提出的方法在低转速情况下存在较大的误差。将来的研究可以瞄准解决低转速情况下的问题，用来解决这一问题的途径包括通过提取比振动RMS更加有效的状态特征，或者使用声发射传感器代替加速度传感器等。

另外，轴承工况的变化不仅包括转速的变化，还包括载荷的变化。阈值模型的自适应参数应该是振动RMS、转速和载荷的多变量函数。如果提取的特征有多个，那么这些特征也将是这些函数的输入变量。在变转速和变载荷情况下的轴承健康监测也值得深入研究。

5结论

本文提出了一种以自适应阈值模型为基础，可以适应不同运行工况的健康监测方法。RVM被选择用于拟合模型参数与工况参数之间的关联关系。由于检测模型是转速的连续函数，因此该方法在任何转速下都可以使用。应用该方法监测轴承健康状态，结果显示监测误差主要集中在低转速情况下；当转速高于600 r/min时，该方法可以有效监测轴承故障。

参考文献(References)

[1]Randall R. Vibration-based condition monitoring: industrial, aerospace and automotive applications [M].USA: A John Wiley and Sons Ltd. Publication, 2011.

[2]Conforto S, D′Alessio T. Spectral analysis for non-stationary signals from mechanical measurements: a parametric approach[J]. Mechanical Systems & Signal Processing, 1999, 13(3):395-411.

[3]Lin J,Qu L S. Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis[J]. Journal of Sound & Vibration, 2000, 234(1):135-148.

[4]Lee J W, Kim J D, Yun C B, et al. Health-monitoring method for bridges under ordinary traffic loadings[J]. Journal of Sound & Vibration, 2002, 257(2):247-264.

[5]Cheng J S, Yu D J, Yang Y. Research on the intrinsic mode function (IMF) criterion in EMD method [J]. Mechanical Systems and Signal Processing,2006, 20(4):817-824.

[6]Roveri N, Carcaterra A. Damage detection in structures under traveling loads by Hilbert-Huang transform [J]. Mechanical Systems and Signal Processing, 2012, 28(2):128-144.

[7]Fyfe K R, Munck E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997, 11(2):187-205.

[8]Li H, Zhang Y P, Zheng H Q. Gear fault detection and diagnosis under speed-up condition based on order cepstrum and radial basis function neural network [J]. Journal of Mechanical Science and Technology, 2009, 23(10):2780-2789.

[9]Wang Y J, Kang S Q, Jiang Y C, et al. Classification of fault location and the degree of performance degradation of a rolling bearing based on an improved hyper-sphere-structured multi-class support vector machine [J]. Mechanical Systems and Signal Processing, 2012, 29:404-414.

[10]Widodo A,Yang B S. Support vector machine in machine condition monitoring and fault diagnosis [J]. Mechanical System and Signal Processing,2007, 21(6):2560-2574.

[11]Hu L, Hu N Q, Zhang X P, et al. Novelty detection methods for online health monitoring and post data analysis of turbopumps[J]. Journal of Mechanical Science and Technology, 2013, 27(7):1933-1942.

[12]谢光军，胡茑庆，胡雷. 涡轮泵实时故障检测的改进自适应相关阈值算法[J]. 推进技术, 2006, 27(1): 5-8.

XIE Guangjun, HU Niaoqing, HU Lei. Improved adaptive correlation thresholds algorithm for turbopump real-time fault detection[J]. Journal of Propulsion Technology, 2006, 27(1): 5-8. (in Chinese)

[13]Tipping M E. Sparse bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.

[14]Maio F D, Tsui K L, Zio E. Combining relevance vector machines and exponential regression for bearing residual life estimation [J]. Mechanical Systems and Signal Processing, 2012, 31(8):405-427.

[15]Gebraeel N, Elwany A, Pan J. Residual life predictions in the absence of prior degradation knowledge[J]. IEEE Transactions on Reliability, 2009, 58(1):106-117.

Bearings health monitoring under varying operation conditions using relevance vector machine and adaptive threshold model

HULei1,2,FANBin1, 2,HUNiaoqing1, 2,GAOMing1

(1.College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China;2.Laboratory of Science and Technology on Integrated Logistics Support, National University of Defense Technology, Changsha 410073, China)

Abstract：Operation conditions usually change when rotating machinery works. The changing operational conditions and machine fault can make the mechanical vibration characteristics change and cause diagnosis errors, so a new method for the health monitoring of bearings under changing operational conditions was proposed. In this method, the RVMs (Relevance Vector Machines) were used for obtaining the continuous function relationships between the adaptive parameters of the threshold model and the characteristic statistics of vibration features. Based on the characteristic statistic in different operation conditions, the adaptive threshold model was constructed. This method was used for bearings health monitoring at different revolving speed. Monitoring results show that this method is effective only when the rotational speed is higher than a relative small value.

Key words：health monitoring; relevance vector machine; adaptive threshold model; varying operation conditions; bearings

中图分类号：TP305； V434.21

文献标志码：A

文章编号：1001-2486(2016)01-168-07

作者简介：胡雷(1981—)，男，安徽界首人，讲师，博士，E-mail：hulei@nudt.edu.cn

基金项目：国家自然科学基金资助项目(51575518，51475463)

*收稿日期：2014-12-20

doi:10.11887/j.cn.201601027

http://journal.nudt.edu.cn