激光陀螺零偏误差复合信号补偿分析*

李　耿，张鹏飞，龙兴武

(国防科技大学 光电科学与工程学院， 湖南 长沙　410073)



激光陀螺零偏误差复合信号补偿分析*

李耿，张鹏飞，龙兴武

(国防科技大学 光电科学与工程学院， 湖南 长沙410073)

摘要：作为一种集成了光学、电学和机械力学的复杂系统，激光陀螺可以精确地测量物体的角速率输出。为了满足惯性导航系统长时、高精度的测量要求，研究了激光陀螺内部不同类型的传感器与激光陀螺零偏误差之间的特性；在传统的基于温度的零偏误差补偿方法的基础上，引入二频机抖激光陀螺内部温度传感器、光电二极管和粘在抖动机构上的压电陶瓷的输出信息进行复合建模；利用非线性拟合能力强的支持向量机算法，针对不同类型信息与二频机抖激光陀螺零偏误差的相关性对模型进行优化。实验结果表明，该二频机抖激光陀螺零偏误差补偿模型的补偿精度高于传统的补偿方法。

关键词：激光陀螺；复合信号；零偏误差补偿

激光陀螺是一种复杂的光-机-电一体化系统[1]，能够以很高的精度对物体的角速率进行测量。其测量的原理是基于Sagnac效应，即在光学谐振腔中两束相向传播的激光在有角速率输入的情况下会产生与角速率成比例的干涉条纹输出。通过鉴相解调等方法可以得到激光陀螺相对于惯性空间的角速率值。但是，要想获得高精度的角速率输出，还必须尽量减小激光陀螺的零偏误差，因为在长时、高精度的激光陀螺惯性导航系统中，单个惯性器件的精度，尤其是激光陀螺的精度将最终决定导航系统的精度。为了减小激光陀螺的零偏误差，传统的方法是通过采集激光陀螺内部温度传感器的信号对零偏误差进行补偿。这些温度传感器安装在激光陀螺光学腔的腔体外部以及激光陀螺外壳内壁上[2]。关于温度传感器的数量和安装位置等因素对激光陀螺零偏误差补偿效果的影响,文献[2]进行了详细介绍。同时，针对激光陀螺零偏误差的各种温度补偿模型和补偿算法，许多学者也进行了研究，其中包括最小二乘拟合法、人工神经算法、支持向量机算法等[3]。另外，激光陀螺的其他输出信息，例如用于激光陀螺稳频控制的光强信号、用于消除二频机抖激光陀螺(Mechanically Dithered Ring Laser Gyroscope, MDRLG)闭锁效应的抖动机构的频率信号等也被用于激光陀螺的零偏误差补偿[4-5]。文献[6]还指出激光陀螺合光棱镜的读出信号的差值也可以用于补偿激光陀螺的零偏误差。然而上述这些文献中的激光陀螺零偏误差补偿方法均是利用了单一的补偿信号，而这些信号之间的关联信息并没有被利用。因此，研究能够将这些来自不同传感器的补偿信号整合起来的技术就变得非常重要。同时，还需要有效地处理由此带来的大量数据与零偏误差之间的计算效率问题。

复合信息融合技术最早是美国军队C3I系统应对战场信息的采集和处理需求而开发和应用的[7]。在此之后，复合信息融合技术逐渐与其他算法相结合并应用到更多领域，其中就包括与支持向量机算法的结合与应用[8]。相较于需要启发式学习方法及较多先验信息的神经网络算法，支持向量机算法有如下一些优势：1)可以避免局部最小化问题的出现；2)对采样信息的数量和质量没有严格的要求；3)有较强的泛化能力。利用支持向量机算法结合复合信息融合技术可以有效地提高不同类型传感器间的耦合信息，从而提高激光陀螺零偏误差模型的补偿能力。

1激光陀螺零偏误差补偿模型

对于想要建立激光陀螺零偏误差补偿模型的研究人员来说，与其相关的各种信息都可以作为模型中的参数，其中就包括了温度信息、电学信息、光学信息及力学信息等。而温度信息是目前激光陀螺零偏误差补偿模型中最常用的参数，它反映了激光陀螺在工作条件下周围环境及激光陀螺光学谐振腔内部的热学环境。利用粘贴在激光陀螺光学谐振腔表面及激光陀螺安装壳体内部的温度传感器采集的相应点的温度值和与其同步采集的激光陀螺零偏输出值可以建立如式(1)所示的多项式方程：

(1)

式中，B是激光陀螺的零偏误差，T是激光陀螺上的温度，dT/dt是温度的变化率，ΔT是不同温度传感器之间的温度梯度，而ai(i=0,1,2,3,4)是最小二乘拟合系数。

文献[4]考察了基于光强信号的激光陀螺零偏误差补偿模型(所用的光强信号是激光陀螺稳频系统中用来稳定激光陀螺腔长的直流光电管输出信号)，并利用得到的光强信号和激光陀螺零偏误差信号建立了相应的补偿模型：

B=f(I)=b0+b1I+b2dI/dt

(2)

式中，I是激光陀螺上的光强，dI/dt是光强的变化率，b0,b1和b2是模型拟合系数。

另外一种可以利用的信息来自于二频机抖激光陀螺的机械抖动机构[5]，该机构可消除激光陀螺的闭锁效应。通过安装在激光陀螺光学谐振腔中心孔内的机械抖动轮使激光陀螺的环形光路以机械抖动轮的谐振频率快速地通过锁区可以有效地消除激光陀螺的闭锁效应。而机械抖动轮的谐振频率并不是保持不变的，随着外界环境及自身抖动功耗的增加，谐振频率也会发生相应的变化。二频机抖激光陀螺的抖频稳定系统就是要使驱动机构的频率能够跟踪机械抖动轮变化的谐振频率，从而保持抖动幅度的稳定。经过实验测试，二频机抖激光陀螺机械抖动轮的谐振频率与温度的关系如式(3)所示：

B=f(v)=c0+c1v+c2dv/dt

(3)

式中，v是二频机抖激光陀螺机械抖动轮的谐振频率，dv/dt是谐振频率的变化率，c0,c1和c2是模型拟合系数。

然而，在上述的激光陀螺零偏误差补偿模型中，每种信息仅仅是作为单一种类的信息单独用于激光陀螺的零偏误差补偿模型中，不同种类信息之间及其与激光陀螺零偏误差之间的关系被忽略掉了。显然，从激光陀螺不同种类的传感器中采集到的信息与激光陀螺的零偏误差之间有着不同的特征关系，而且并非是理想的线性关系。本研究的目的就是利用基于支持向量机的多传感器信息融合技术将这些采集到的大量数据进行处理，从而最大限度地减小激光陀螺的零偏误差，提高惯性导航系统的精度。

2基于支持向量机的信息融合模型

2.1支持向量机模型

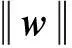
(4)

式中，C为罚函数系数，而ξi≥0(i=1,2,…,k)为松弛系数。利用核函数方法，上述线性支持向量机模型可以拓展到非线性可分的领域。输入数据可以在一个新的高维空间中用正定核函数来表示，而且该正定核函数满足Mercer条件Φ(xi)Φ(xj)=K(xi,xj)。最终的超平面判定函数可以用式(5)表示：

(5)

式中，ai为Lagrange乘子。Φ函数的具体形式可以不用考虑，只要确定核函数K(xi,xj)即可。一种广泛较为广泛的核函数为高斯径向基函数(Gaussian Radial Basis Function， GRBF)：

(6)

其中核函数参数γ和C是通过模型的训练过程来决定的。最终的判定输入方程为：

d(x)=sgn[f(x)]

(7)

2.2基于子模块支持向量机的复合信息融合方法

复合信息融合模型是一个需要处理大量数据的复杂系统，对于二频机抖激光陀螺来说，就是要将与其相关的温度、光强、抖频等不同类型的传感器信号汇总起来进行相关分析和判定。考虑到直接耦合方法的一些不足，如不确定性、较差的鲁棒性和灵活性，故引入权重结构来对激光陀螺的复合信息进行预处理。设定激光陀螺零偏误差补偿模型可以分为M个子模型，而每个子模型中包括了N种类型的数据，将支持向量机算法应用到每个子模型中，这样在每个子模型中即可以首先对经过融合后的激光陀螺零偏误差补偿模型进行一次计算，之后再对M个子模型的计算结果与零偏误差作相关性分析，进而判定权重系数并最终对激光陀螺的零偏误差进行补偿，计算表达式如式(8)所示：

(8)

式中，Sf(x)是经过融合处理后的二频机抖激光陀螺零偏误差，λ=(λ1,λ2,…,λM)T是实权重向量，M是子模型的数量，Sm(x)是第m个二频机抖激光陀螺零偏误差补偿子模型的输出。

基于复合信号的二频机抖激光陀螺零偏误差补偿算法的流程图如图1所示。

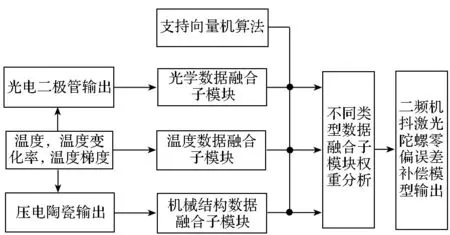
图1　采用不同类型数据融合网络的二频机抖激光陀螺零偏误差补偿模型Fig.1　MDRLG drift error compensation model using compound signals of different types of sensor data

在图1所示的数据融合网络中，二频机抖激光陀螺上温度传感器采集到的温度值、不同时间间隔计算出的温度变化率以及不同温度传感器之间的温度梯度均整合在一个温度数据融合补偿子模块中。而来自于二频机抖激光陀螺敏感谐振腔内激光光强变化的光电二极管的输出信号通过与温度数据的融合组成了光学数据融合补偿子模块。同样的，从二频机抖激光陀螺机械抖动机构中检测抖动轮谐振频率的压电陶瓷上输入的信号与温度数据融合组成了机械结构数据融合补偿子模块。于是，这些子模块的输出经过式(8)分析可以得到二频机抖激光陀螺零偏误差补偿的最终输出结果。

3实验及结果分析

模型验证实验是在实验室自研的二频机抖激光陀螺惯导系统上进行的。首先将惯导系统安装在高低温实验箱中，用来模拟惯导系统工作时外部环境温度的变化。为了考察二频机抖激光陀螺在全温域的零偏特性，模型验证实验设定高低温实验箱的温度实验曲线剖面如图2所示，高低温实验箱的温度控制精度为0.1 ℃。

图2　高低温实验箱的温度实验曲线剖面Fig.2　Configuration curve of temperature in the chamber

其次在常温下将惯导系统上电开启，用电脑采集从惯导系统中输出的二频机抖激光陀螺的各种输出信号，包括各温度传感器的温度、输出光强和机械抖动轮的谐振频率信号，用于和二频机抖激光陀螺的零偏信号进行补偿计算。图3为二频机抖激光陀螺的零偏信号在温度变化条件下与不同传感器输出信号之间的关系。由图可知，其为非常复杂的非线性关系，而且每种传感器的信号与二频机抖激光陀螺零偏的相关性都有各自不同的特点。

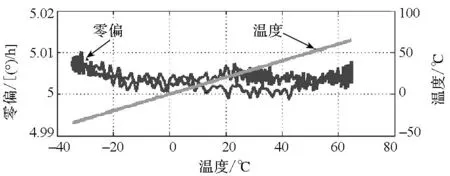
(a) 二频机抖激光陀螺零偏与温度的关系(a) Relation between MDRLG drift and temperature

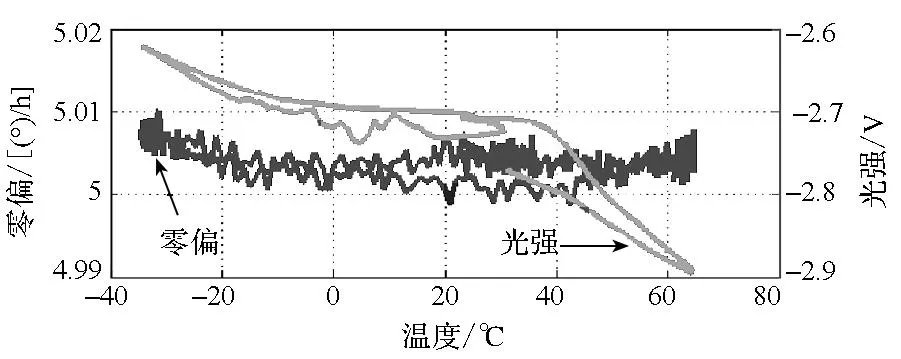
(b) 二频机抖激光陀螺零偏与光强的关系(b) Relation between MDRLG drift and light intensity

(c) 二频机抖激光陀螺零偏与抖动频率的关系(c) Relation between MDRLG drift and dither frequency图3　不同类型的传感器数据与二频机抖激光陀螺零偏的关系Fig.3　MDRLG drift for different types of sensor data

图4为利用支持向量机方法对不同数据融合子模块进行计算而得到的二频机抖激光陀螺零偏误差曲线。从图中可以看出，对于不同类型的数据融合子模块，二频机抖激光陀螺零偏误差曲线有着不同的特点：在温度数据融合子模块中，低温部分的补偿效果较差而高温部分的补偿效果较好；在机械结构数据融合子模块中，补偿结果的离散度较大，高温时这种表现则更加明显；光学数据融合子模块的补偿效果在三个子模块中是最好的，补偿曲线较平而且离散度较小。采用Allan方差分析方法对二频机抖激光陀螺的原始数据和经过不同类型数据融合子模块补偿后的结果进行比较，如表1所示，其中Q、N、B、K、R分别表示量化噪声、角度随机游走、零偏不稳定性、角速率随机游走、速率斜坡。

(a) 二频机抖激光陀螺零偏误差在温度子模块中的补偿结果(a) Result of MDRLG drift error compensation in temperature sub-module

(b) 二频机抖激光陀螺零偏误差在光学子模块中的补偿结果(b) Result of MDRLG drift error compensation in optical sub-module

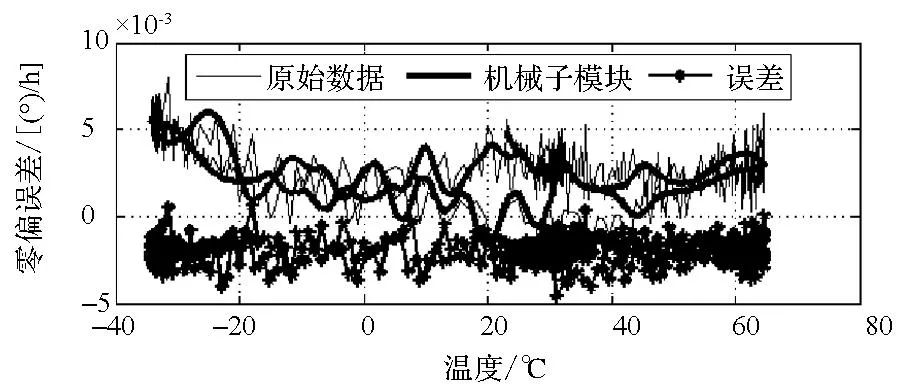
(c) 二频机抖激光陀螺零偏误差在机械子模块中的补偿结果(c) Result of MDRLG drift error compensation in mechanical sub-module图4　二频机抖激光陀螺零偏误差在不同子模块中的补偿结果Fig.4　Results of MDRLG drift error compensation in different sub-modules

表1中的零偏不稳定性在三个子模块中的精度差异体现了不同类型传感器与二频机抖激光陀螺零偏误差之间的不同特点：1)对于温度子模块来说，由于温度传感器的采集与计算相比二频机抖激光陀螺本身的零偏变化来说有一个弛豫时间，因此无法及时地反映二频机抖激光陀螺输出角速率的实时变化；2)对于光学子模块来说，所用的光强信号是从直接参与二频机抖激光陀螺敏感角速率的激光光束中取得的，因此能够较好地实时反映二频机抖激光陀螺零偏的变化；3)对于机械子模块来说，机械结构数据融合子模块中的二频机抖激光陀螺零偏误差补偿结果在高温区域的离散度增加，是由于在高温时二频机抖激光陀螺机械抖动轮材料的杨式模量降低，即抖动轮变软，从而其品质因数下降导致的非线性因素增加而出现的现象。通过对不同类型传感器数据与二频机抖激光陀螺零偏误差的特征关系的分析，可以确定各数据融合子模块在总模型中的权重系数并得到最终的二频机抖激光陀螺零偏误差补偿曲线，如图5所示。

表1　二频机抖激光陀螺各项随机误差的

图5　基于复合信息的二频机抖激光陀螺零偏误差补偿结果Fig.5　Result of MDRLG drift error compensation in compound module

从图中可以看出，经过对各数据融合子模块进行权重计算后，二频机抖激光陀螺的零偏误差得到了有效抑制，精度也有大幅度的提高，经过补偿后的二频机抖激光陀螺零偏误差中的零偏不稳定项从未补偿的0.027 8(°)/h提高到了0.004 6 (°)/h。这清楚地说明所采用的基于复合信号的二频机抖激光陀螺零偏误差补偿方法相较于传统的单一信号的二频机抖激光陀螺零偏误差补偿方法更有效。

4结论

本文构建了一种基于复合信号，应用支持向量机方法的二频机抖激光陀螺零偏误差补偿模型。通过将二频机抖激光陀螺内部温度传感器、光电二极管、压电陶瓷等不同类型的传感器信号采集出来，研究其与二频机抖激光陀螺零偏误差之间的关系并建立了三种不同类型的数据融合子模块，经过分析确定了各子模块在总的二频机抖激光陀螺零偏误差补偿模型中的权重系数，完成了二频机抖激光陀螺零偏误差复合信号补偿模型的搭建。实验结果表明，该模型可以有效地补偿二频机抖激光陀螺的零偏误差，相比于传统基于温度的单一信息补偿模型，其精度也有很大提升。

参考文献(References)

[1]Faucheux M, Aucheux M, Fayoux D, et al. The ring laser gyro[J].Journal of Optics, 1988, 19(3):101-115.

[2]Guo C, Xu Y J, Zhao X N. Investigation on the temperature compensating model for ring laser gyroscope [J]. Chinese Optics Letters, 2006, 4(10): 576-579.

[3]Wei G, Li G, Long X W, et al. Application of least squares-support vector machine in system level temperature compensation of ring laser gyroscope [J].Measurement, 2011, 44(10):1898-1903.

[4]张鹏飞， 王宇， 于旭东， 等. 光路温度特性对激光陀螺零偏的影响 [J]. 红外与激光工程， 2011, 40(12): 2393-2397.

ZHANG Pengfei, WANG Yu, YU Xudong, et al. Effect of temperature characteristic of light path on RLG′s bias [J]. Infrared and Laser Engineering, 2011, 40(12): 2393-2397. (in Chinese)

[5]张鹏飞， 龙兴武. 二频机抖激光陀螺抖动频率与温度关系的研究 [J]. 激光技术， 2006, 30(5):523-525.

ZHANG Pengfei, LONG Xingwu. Research of the relation between dither frequency and temperature in mechanically dithered ring laser gyro [J]. Laser Technology, 2006, 30(5): 523-525. (in Chinese)

[6]Li G, Wang F, Xiao G Z, et al. Temperature compensation method using readout signals of ring laser gyroscope [J]. Optics Express, 2015, 23(10):13320-13332.

[7]Huang X H, Wang M. Multi-sensor data fusion structures in autonomous systems: a review [C]//Proceedings of IEEE International Symposium on Intelligent Control, 2003: 817-821.

[8]Vapnik V, Chapelle O. Bounds on error expectation for support vector machines [J]. Neural Computation, 2000, 12(9):2013-2036.

Study on the bias error compensation of ring laser gyroscope based on compound signals

LIGeng,ZHANGPengfei,LONGXingwu

(College of Optoelectronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：As a complex system combined with optics, electronics and mechanics, the RLG (ring laser gyroscope) can measure the angle rate with high accuracy. In order to meet the requirement of longer-time and higher precision in inertial navigation system, the characteristics between the RLG drift error and different signals from various sensors were studied. Based on the traditional RLG drift error compensation model, the compound signals from thermometers, photodiodes and piezoelectric ceramics attached on the dithered mechanism were introduced into the model. Moreover, by utilizing the support vector machine algorithm which has good nonlinear fitting capacity, the model was optimized by the correlation features between the mechanically dithered RLG drift error and the compound signals. The experimental results show that the precision of the mechanically dithered RLG drift error compensation model is higher than the traditional one.

Key words：ring laser gyroscope; compound signals; drift error compensation

中图分类号：TN744.5

文献标志码：A

文章编号：1001-2486(2016)01-163-05

作者简介：李耿(1978—)，男，山西太原人，讲师，博士研究生，E-mail：lg_163@163.com

基金项目：国家自然科学基金资助项目(61503399)

*收稿日期：2015-09-30

doi:10.11887/j.cn.201601026

http://journal.nudt.edu.cn