运用动态规律 提升想象能力——例析动态规律在柱体体积计算公式推导与运用的实践
2016-04-08浙江杭州市萧山区万向小学311200朱燕锋
浙江杭州市萧山区万向小学(311200)朱燕锋
运用动态规律提升想象能力——例析动态规律在柱体体积计算公式推导与运用的实践
浙江杭州市萧山区万向小学(311200)朱燕锋
[摘要]数学知识来源于生活,尤其是图形类知识,在现实生活中都能找到原型,在多姿多彩的世界里,只要用心观察,处处是图形,处处是数学。教师要充分利用学生现有的基本生活经验,正确引导学生用数学的眼光去关注、去体会美丽多彩的世界,从而把课堂教学中学到的数学知识与实际生活联系起来。借助几何直观,发展学生的空间想象能力,开展综合实践活动。
[关键词]数学原型图形运动模型思想几何直观
2011版数学课程标准提出:在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。为了适应时代发展对人才培养的需要,数学课程还要特别注重发展学生的应用意识和创新意识。渗透模型思想和借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。几何直观可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用。
学生其实很早就在实际生活中接触过平移和旋转的知识,例如一个人在行走的过程中就是人的平移或位移,体育课中的四面转法就是旋转……学生对于图形的运动方式理解起来应该不难。因此,在刚接触规则柱体时,教师就应该渗透规则柱体可以看成是由基础图形运动形成的模型思想,联系生活实际,发展学生的空间想象能力,为后续的深入教学进行铺垫。
以人教版数学六年级下册关于圆柱的体积计算公式的推导为例,圆柱的体积计算是在六年级上册学习了圆的知识的基础上才研究的课题,课本介绍了圆柱可以看成是由长方形绕其中一边旋转而成,但没有深入介绍其中的知识点,没有介绍和提及“圆柱可以看成是由圆平移一定距离形成的”。因此,关于此类知识点的习题,学生错误率比较高,造成这种现象的其中一个重要原因是学生的空间想象能力欠缺,没有得到最大限度的开发和利用。事实上,教师可先让学生自学课本上介绍的方法,课堂上着重介绍圆柱的形成过程,让多种思维方式发生碰撞,碰撞出智慧的火花。
【思维方式一】圆柱可以看成是由圆平移一定的距离形成的运动轨迹。
教师课前准备了大量的圆形垫片,在学生进行摆拼和拆分的实践操作后提问:“在摆拼的过程中,形成的图形是什么图形?(圆柱)摆拼的长度或高度是圆柱的什么?(高)圆形垫片是圆柱的什么?(底面)摆拼出来的圆柱占了一定的空间,这在数学中是什么?(圆柱的体积)现在你能说出圆柱的体积是怎么计算的吗?(圆柱的体积=底面积(圆的面积)×高(摆拼的长度或高度))”在一步一步推导出“圆柱的体积=圆周率×半径的平方×高”后利用多媒体设备将圆柱的形成过程进行演示,加深学生的理解,发展学生的空间想象能力,最后引导学生寻找生活中的实例,如筒状月饼、圆形饼干的包装等。通过上述的教学,学生一定牢牢记住了圆柱体积的计算公式。

图1面动成体——圆经过平移成圆柱
在拆分(一分为二)的过程中,引导学生观察并提问:“圆柱的什么发生了变化,什么没有发生变化?(表面积发生了变化,体积不变)表面积是增加还是减少?(增加)增加了多少?(两个底面积即两个圆的面积)在合并(二合为一)的过程中,表面积是增加还是减少?(减少)减少了多少?(两个底面积即两个圆的面积)这个过程其实在我们的生活中也是经常出现的,即物体的横切,表面积增加(减少)的是2个横切面——底面。如切黄瓜、锯木头等。”
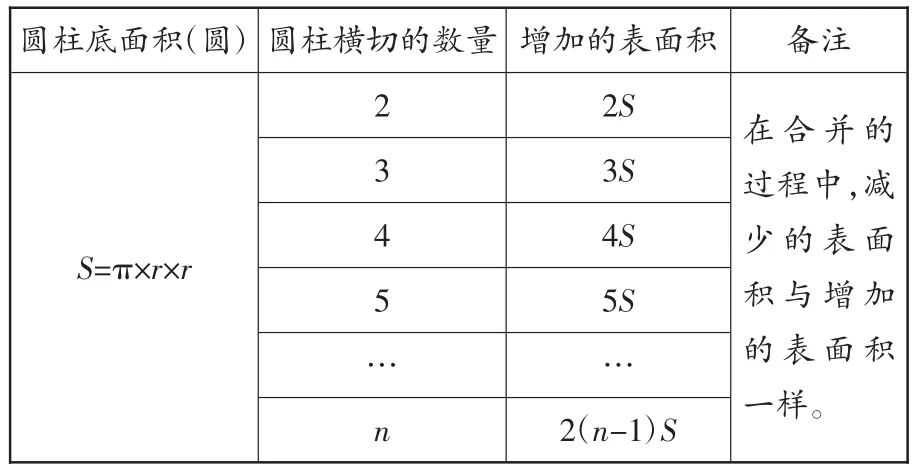
圆柱底面积(圆)圆柱横切的数量增加的表面积 备注S=π×r×r 2 2S 在合并的过程中,减少的表面积与增加的表面积一样。5 5S……n 2(n-1)S 3 3S 4 4S
经过对一系列问题的探究,在解决圆柱体横切表面积增加(减少)的问题时,学生自然就没有困难了。
最后教师进行归纳提升:“圆柱体有这样的规律,其他的规则柱体,如长方体、正方体等是不是也可以这样来理解?”举例:书本、方形饼干等。
通过多媒体演示建立模型,给学生渗透模型思想。

图2长方形或正方形经过平移成正方体或长方体
例1(小学数学六年级下册导学新作业(B)第10页第3题)如图3所示是一个柱体,高为15厘米,底面是一个半径为4厘米、圆心角为270度的扇形,求这个柱体的体积。
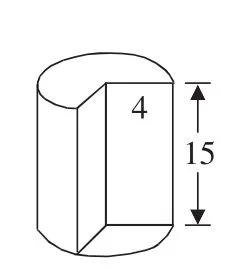
图3
解析:由题已知该柱体的底面是一个半径为4厘米、圆心角270度的扇形,高为15厘米,要求这个柱体的体积,即可以把这个柱体看成是一个由四分之三圆向上或向下平移15厘米形成的。列式为“π×4×4×15=180π(立方厘米)”。
例2(小学数学六年级下册导学新作业(B)第11页第2题)一根2米长的圆柱形木材,横截成3段后,表面积增加了80平方厘米。这根木材的体积是多少?
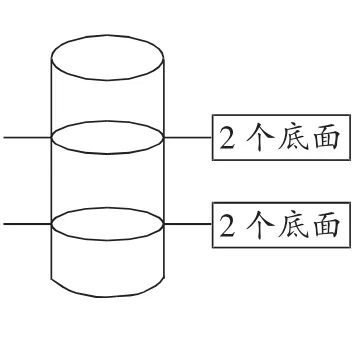
解析:本题要考虑两个问题。(1)单位不统一,首先要换算单位,2米=200厘米;(2)求体积,没有图,比较直观的方法是画出图形,借助图形解决问题。
圆柱体横截成3段后,表面积增加了80平方厘米,即圆柱横切增加4个相等的底面,4个相等的底面等于80平方厘米。故列式为“80÷4×200=4000(立方厘米)”。
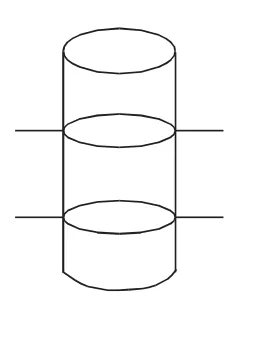
例3有3个底面相等、长是5分米的圆柱体,将它们拼成一个圆柱体,表面积减少了120平方分米,拼成后的长方体体积是多少平方分米?
解析:首先要画出图形,借助图形解决问题。3个相等的圆柱体拼成一个圆柱体,表面积减少120平方分米,即减少了4个底面,4个底面的面积等于120平方分米,高变成了“5+5+5=15(分米)”,故列式为“120÷4×15=450(立方分米)”。
【思维方式二】圆柱可以看成是由长方形或正方形绕其一边旋转而成的运动轨迹。
让学生尝试转动课前准备的一面带柄的长方形小旗(硬质)后思考:“在小旗转动的过程中,形成了一个什么图形?(圆柱)小旗的宽度是什么?(圆柱的高)小旗的长度是什么?(圆柱的底面半径)在转动的过程中小旗占有了一定的空间,是什么?(圆柱的体积)圆柱的体积可以怎么计算?(圆柱的体积=圆周率×半径的平方×高,即圆柱的体积=底面积×高)”教师利用多媒体演示转动的过程,引导学生在生活中找到对应的数学模型,如酒店的旋转门等。

图4面动成体——长方形或正方形绕长或宽旋转一周形成圆柱体
学生探究后发现:在转动的过程中,当长方形或正方形绕长或宽旋转到180度时,相当于把圆柱纵切成相等的两份,表面积增加了4个长方形或正方形的面积,即增加的表面积=半径×高×4或直径×高×2。

纵切面面积 圆柱增加的表面积S=dh=2rh 2S
教师通过引导学生想象“一个半圆形绕直径旋转一周形成(球体),一个直角梯形绕高旋转一周形成(水桶体),一个直角三角形绕直角边旋转一周形成(圆锥)……”发展学生的空间想象能力,让学生在头脑中建立数学模型。
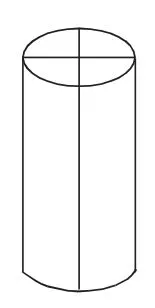
图5
例4(小学数学六年级下册导学新作业(B)第13页第3题)把一根圆柱形木料沿底面直径和高切成大小相等的4份,如图5,表面积增加了800平方厘米,已知圆柱的底面半径是5厘米,这根木料的体积是多少?
解析:沿底面和高切成大小相等的4份,即纵切,增加8个以底面半径为宽的长方形,8个以底面半径为宽的长方形的面积等于800平方厘米,可以求出1个长方形的面积“800÷8=100(平方厘米)”,然后求出长方形的长,即圆柱体的高“100÷5=20(厘米)”,最后利用圆柱的体积公式求圆柱的体积,列式为“5×5×π×20=500π(立方厘米)”。
例5(小学数学六年级下册导学新作业(B)第66页填空题第10题)如图6所示,把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积和原来比增加了80平方厘米,那么圆柱的高是()厘米,长方体的体积是()立方厘米。
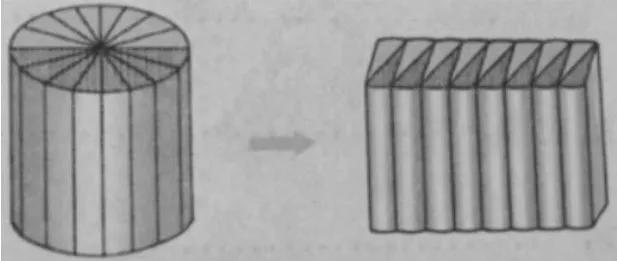
图6
解析:如图6所示,圆柱纵切后拼成近似的长方体,表面积增加了1个以底面直径8厘米为宽的长方形,即增加了80平方厘米,这时可以求出长方形的长,即圆柱的高“80÷8=10(厘米)”。利用转化的思想得到圆柱体体积即长方体体积,体积不变,圆柱体积(长方体体积)为“π×4×4×10=160π(立方厘米)”。
在课堂教学时,教师要引导学生从多种思维角度去分析问题、思考问题,让学生形成灵活运用知识解决实际问题的能力。总之,数学来源于生活,但又高于生活,是从生活中抽象出来的,数学教学只有联系学生已有的生活经验,引发学生的思考与想象,才能真正提高学生的数学能力。
(责编童夏)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)08-011
