基于曲线拟合的PEBB单元散热优化设计

陈国栋 刘 宏 王江涛（上海电气输配电集团技术中心 上海 200042）



基于曲线拟合的PEBB单元散热优化设计

陈国栋 刘 宏 王江涛
（上海电气输配电集团技术中心 上海 200042）

摘要散热优化是功率电子元组件（PEBB）设计的关键环节，良好的散热系统可充分提高PEBB的功率密度，最大限度地提高开关器件的利用率。文中详细计算了PEBB单元开关器件的各项损耗功率，并采用ICEPAK软件对该单元进行散热仿真分析。通过改变PEBB单元中散热器的翅片数目和基板厚度等参数，得出其对单元散热效果的影响，运用曲线拟合的方式确定了这些影响因素与散热效果的函数关系，并通过对函数式求极值给出了散热器结构优化方案，最终通过对比仿真结果与实验数据验证了热仿真设计方法和实验的一致性，证明了该仿真在系统散热优化设计中具有指导意义。

关键词：功率损耗 热仿真 ICEPAK软件 参数优化 曲线拟合

上海市科技创新行动计划资助项目（13DZ1200200）。

Thermal Analysis and Optimization of PEBB Unit Based on Curve Fitting

Chen Guodong Liu Hong Wang Jiangtao
（Shanghai Electric Power Transmission & Distribution Group Shanghai 200042 China）

Abstract The cooling optimization design is a crucial part of a power electronics building block (PEBB) unit. A better heat dissipation system increases power intensity of PEBB and keeps insulated gate bipolar transistor (IGBT) modules on well operation. In this paper, power loss of IGBT modules in the PEBB unit is calculated in detail. Thermal simulation on a design example of the PEBB unit is analyzed by the computational fluid dynamics (CFD) software named ICEPAK. By changing structural parameters of the heatsink in the PEBB unit, the influence of parameters on heat transfer performance is obtained. Then the paper presents a structural optimization scheme of the heatsink through a curve fitting and extreme value seeking analysis. Finally the feasibility of thermal simulation is verified by comparing simulation results with experimental data, and the directive significance of the simulation on system-level thermal optimization design is proved.

Keywords：Power loss, thermal simulation, ICEPAK software, parameter optimization, curve fitting

0 引言

近年来，电力电子设备逐渐小型化，其结构设计趋向紧凑，使得柜体内散热问题变得愈加严峻。随着大功率电力电子器件的发展[1,2]，其容量不断得到提高，发热量也随之上升。绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor，IGBT）模块是功率电子组件（Power Electronics Building Block，PEBB）单元的主要热源，当其处于频繁开通、关断的工作状态时，由于电力电子器件本身对温度较为敏感，一旦温度超过其额定温升范围，在自身热量的长期作用下会产生失效，工作寿命和可靠性受到极大影响[3,4]，严重时将影响整个系统的正常运行。因此有必要对电力电子设备中PEBB单元的散热情况进行深入研究。

目前关于电力电子设备热耗计算和散热系统优化设计的研究已逐渐成为热点[5-10]。文献[5]建立单极性和双极性两种脉冲宽度调制（Pulse Width Modulation，PWM）方式下的快速IGBT损耗计算方法，并与厂家提供的IPOSIM6—2a软件计算结果进行对比，验证了该方法具有较高的计算准确度。文献[6,7]均考虑芯片结温对各种损耗影响，文献[6]提出了一种IGBT模块损耗的计算方法，由热阻等效电路得到散热系统各点温度的计算公式，设计了一套强迫风冷散热系统。文献[8]计算75kV·A三电平背靠背变流器内部热源，建立散热系统热阻等效网络，估算当功率器件结温处于最高临界值时所允许的散热器热阻最大值，分析母线功耗、器件损耗和风机风量对变流器热分布的影响，并在计算流体动力学（Computational Fluid Dynamics，CFD）有限元软件中通过调整进风口的开孔率完成对散热系统的优化设计以达到较好的散热效果。文献[9]采用ICEPAK软件对所设计的散热器进行仿真分析，对电子产品内的传热和空气流动情况进行模拟，与理论计算结果相近，说明其散热系统满足设计要求，该文献对散热系统的分析研究均较为详细，但如何从散热核心部件散热器的角度考虑优化设计方案仍待进一步研究。文献[10]选定某一典型型材散热器，研究散热器翅片长度、厚度、高度和个数等几何因素对其热性能的影响情况。采用散热器优化设计软件Qfin改变散热器的几何参数，有效降低其热阻，为型材散热器的选择及优化设计提供依据，但文中选取的几何参数仅为原型和优化后的两组数据，各项参数对系统散热效果的影响规律尚待分析。

本文首先对IGBT模块的功率损耗进行近似计算。作为PEBB单元中的主要热量来源，IGBT模块紧密贴合分布在该单元中某一特定结构的矩形翅片式散热器的基板上，文中采用ICEPAK软件对该情况进行仿真计算，评估其是否达到整个系统的散热要求。其次通过改变PEBB单元中散热器的几何参数，借助ICEPAK仿真工具进行不同翅片数目和不同基板厚度情况下的仿真分析。在获得大量仿真数据的基础上，通过曲线拟合的方法建立影响因子条件下的参数寻优函数，实现了散热器设计中关键参数的最优求解，提出了一种基于曲线拟合方法的散热器优化设计方法，并根据最优求解值制作了一套PEBB单元实验装置，最终通过仿真数据和实验数据的对比，证明了所提的散热器优化设计方法实用有效，具备一定的工程借鉴价值。

1 IGBT模块的功率损耗简化计算

IGBT模块一般内部集成有IGBT晶体管和反并联续流二极管（Free Wheeling Diode，FWD），因此IGBT模块的功耗Ptot包括IGBT晶体管的稳态损耗Psat、开关损耗Psw和FWD的稳态损耗PF、反向恢复损耗Prr[6]。

1.1 IGBT晶体管的稳态损耗Psat

IGBT晶体管的稳态损耗是指IGBT处于导通状态下产生的损耗，当晶体管的开关频率较低时，该损耗在总损耗中占主要部分[11]。单个IGBT稳态损耗的通用计算公式为[12]

式中，vCE是晶体管集电极和发射极间的管压降；iC是晶体管集电极电流；τ 是占空比。

文献[13]首先进行实验测量，再根据该测量数据插值计算某次开关过程中特定电压、结温和电流情况下的损耗，损失功率即为周期内多次开关过程中的累积，这种方法虽然较为准确，但过程较复杂；文献[6,14]提出将初始饱和压降VCE0和导通电阻rCE与温度的关系近似线性化的方案，文献[9,15]根据IGBT集射极电压饱和特性曲线近似拟合饱和压降和通态电流的线性关系表达式，但需要的参数较多。本文为简化计算，采用导通状态下IGBT晶体管集射极压降VCE(sat)的典型值，最终得到在单极性倍频PWM调制下，IGBT晶体管稳态损耗的近似计算公式为[8]

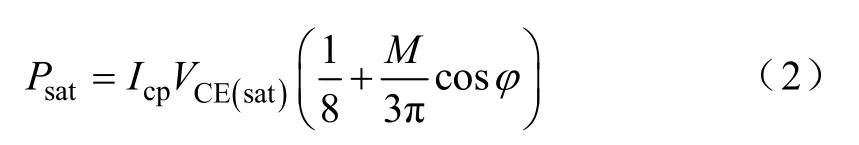
式中，Icp为晶体管集电极电流峰值；VCE(sat)为晶体管结温Tj=125℃时，峰值电流为Icp情况下IGBT晶体管的饱和压降[16]；M为PWM信号的调制比，cosφ为功率因数。

1.2 IGBT晶体管的开关损耗Psw

IGBT晶体管的开关损耗是指IGBT晶体管在开通和关断过程中产生的功率损耗，当晶体管的开关频率较高时，该损耗在总损耗中所占的比例迅速上升。单个IGBT开关损耗的通用计算公式为[5]

式中，fsw为开关频率；Esw(on)和Esw(off)分别为晶体管开通和关断一次损失的能量。

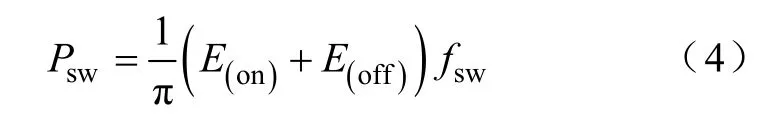
由于在实际应用中，IGBT晶体管所承受di/dt很大，可近似认为Esw(on)和Esw(off)为恒定值，因此该式可简化成式中，E(on)和E(off)为一定直流电压下、Tj=125℃时，峰值电流为Icp的情况下开通和关断一次损失的能量，其值可通过查阅IGBT模块的生产厂家所提供的用户手册获得[6]。

1.3 FWD的稳态损耗PF和反向恢复损耗Prr

由IGBT晶体管的损耗计算可同理得到PF和Prr。FWD的稳态损耗近似计算公式为

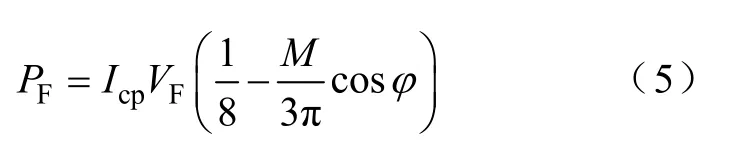
FWD的反向恢复损耗的简化计算公式为

式中，VF为FWD的通态压降；Erec为FWD在承受反向电压过程中产生的反向恢复损耗。

由于本文所提及的模块内部均集成有两个IGBT晶体管和FWD管，由式（2）和式（4）～式（6）可计算IGBT模块的功率损耗的近似计算公式为Ptot=2(Psat+Psw+PF+Prr)。

2 PEBB单元的散热仿真分析

2.1 PEBB单元建模

如图1所示，PEBB单元中IGBT模块的散热方式是：模块通过铜基板底板与散热器接触，热量通过散热器基板传递到翅片，并采用强制风冷的方式降低IGBT模块的温升以保证单元正常运行。

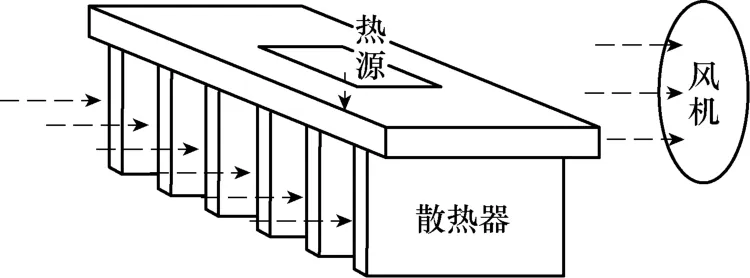
图1 PEBB单元散热示意图Fig.1 Schematic diagram of heat dissipation of PEBB unit

IGBT模块封装在塑料外壳中，芯片用硅胶密封保护，而硅胶的导热系数很低，约为0.8W/(m·K)，因此可认为芯片产生的热量只通过铜基板底板向外界传递，假设模块所产生的热量在底层铜基板上均匀分布，可将IGBT模块简化成薄板。

散热器的基板上嵌有12根热管，热管在同等导热条件下导热能力是铜的1 490倍，这种特别优良的导热性能可实现几乎无温差的导热[17]，改善IGBT内部温度的不均匀性，也可通过蒸发段与冷凝段的温度交换增大散热面积，加强冷却效果。文中忽略热管失效的情形，通过等效导热系数模拟热管。热管具有各向异性的导热系数，在蒸发段到冷凝段蒸汽流动方向上导热系数很大，参数可由生产厂家提供，而在其他两个方向的导热系数则可设置成铜的导热系数。

文中的PEBB单元所使用的是英飞凌公司生产的FF300R12MS4模块，采用单极性倍频PWM信号调制。下面以该单元的电流有效值Ic为105A的情况为例，直流电压为750V、调制比M为0.9、功率因数cosφ为0、开关频率fsw为20kHz，计算FF300R12MS4的功率见表1。

表1 FF300R12MS4功耗Tab.1 Power loss of FF300R12MS4

散热器基板上均匀分布有6块IGBT模块，每块模块的功耗为655.46W，因此系统的总功耗为3 932.76W。

散热器为矩形翅片式，其基板高度为12mm，翅片高度为105mm，除去两侧起支撑作用的两片厚翅片之外共有155片薄翅片，厚度均为1mm。

2.2 散热仿真计算

在CFD软件ICEPAK仿真环境中，由于散热器与空气之间的热传递过程为强迫空气对流换热，因此可忽略IGBT模块、散热器与周围环境之间的辐射换热，将气流场设置为紊流，环境温度设置为户外温度55℃，并根据PEBB单元建模所提供的方法进行简化，建立的模型如图2所示。

图2 PEBB单元仿真模型Fig.2 Simulation model of PEBB unit

对图2中模型的稳态热场进行数值模拟计算，由于型材散热器的工艺限制，文中均为钎焊散热器，仿真中忽略翅片与基板之间焊料热阻的影响。

散热器基板和IGBT模块的温度分布如图3a所示。由图可看出，由于单元中风机往外排风，最低温度值68.74℃出现在散热器靠近进风口的一侧。由热管的温度分布可看出，热管的热端（即紧贴IGBT模块的部分）与冷端（即管中除去热端的其他部分）的温差较小，表现出其优良的均温性。仿真中在左起第2、3块IGBT之间和第4、5块IGBT之间的中间位置分别设置了测温点，其温度分别为79.6℃和79.64℃，温升分别为24.6℃和24.64℃。散热器基板上的最高温度为85.58℃，出现在IGBT模块与散热器接触的区域，根据散热器的热阻计算公式[18]Rtotal=(Tmax-Tamb)/P，可得出其值为0.007 8K/W。根据模块用户手册可得出芯片结-壳和壳-散热器的等效热阻[19]，并根据热阻的定义得出芯片的最高温度值为104.51℃。尽管该值并未超过芯片所允许的最高温度值，但考虑到IGBT周围的电力电子器件所能承受的温度，散热器基板上的最高温度应不超过85℃，因此需要研究散热器结构参数对温度的影响进行改进优化。

图3b为速度分布剖面，空气从风道入口进入单元内部，经过散热器翅片，在翅片之间完成对流换热过程，吸收IGBT模块产生的部分热量，最终由风机排出。最高速度出现在风机处。另外散热器翅片间空气流速较高。

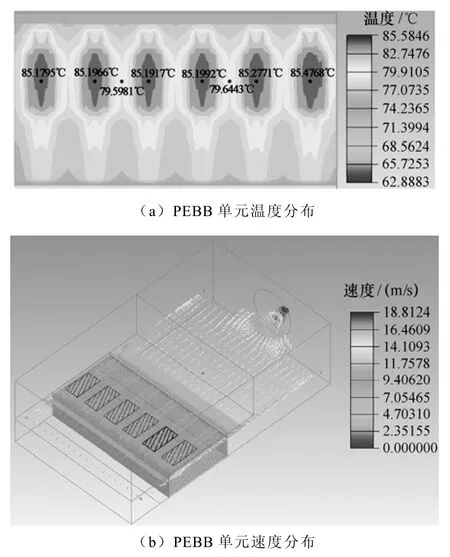
图3 PEBB单元仿真结果Fig.3 Simulation results of PEBB unit

图3c中所示压强为表压，且均为负压。风机处的压强最低，约为-407.384N/m2。由于单元内均为负压，且风机处压强最低，空气从入口处到达风机处最终被排出，风速为0.46m3/s。

3 散热器结构参数对散热效果的影响与结构参数优化

在PEBB单元散热的影响因素中，散热器起到了至关重要的作用，因此本文通过改变散热器的结构参数进行数值仿真以期获得这些参数对散热器热阻乃至整个单元散热的影响情况[20]。

文献[21, 22]提到散热器的总热阻计算公式为

式中，n为翅片的数目；Rth(d)为基板的传导热阻，Rth(d)=a/( WLk)，a为基板厚度，W和L分别为散热器宽度和长度；k为散热器材料的导热系数；Rth(fin)为翅片的传导热阻，Rth(fin)=b/( dLk)，b和d分别为翅片的高度和厚度；Rth(A)为散热器的对流热阻，Rth(A)=1/(hLb)，h为对流换热系数，与翅片间风道宽度、风道内平均速度、流体运动粘度和散热器长度等诸多因素有关[22]。

本文选取翅片数目n和基板厚度a等结构变化参数，在保持散热器其他参数不变的情况下得到散热器基板最高温度随参数的变化值，分析温升变化规律的原因，并根据所得仿真数据采用曲线拟合的方法寻找合适的函数f (x)，通过确定f (x)的未知参数使得拟合误差足够小直至满足准确度为止，最后对f (x)求极值，从而得到结构参数优化的理论依据。

散热器的仿真参数设置如下：散热器翅片高度b=105mm、厚度d=1mm、翅片数目n与基板厚度a为一定范围内的可变参数。

3.1 曲线拟合基本原理

本文所使用的曲线拟合基于最小二乘法，最小二乘法是根据实验数据(xi,yi)(i=1,2,…,m)，通过选取拟合基函数求得函数f (x)，在点xi处函数值f (xi)逐渐逼近观测数据点yi，使得两者二次方和达到最小。其中，拟合基函数为多项式函数1, x, x2,…, xm的拟合方式称作多项式拟合，是最简单且常用的方法。

3.2 改变散热器翅片数目n

设定散热器基板厚度a=12mm，在[100, 400]区间内改变翅片数目n，仿真结果如图4所示。

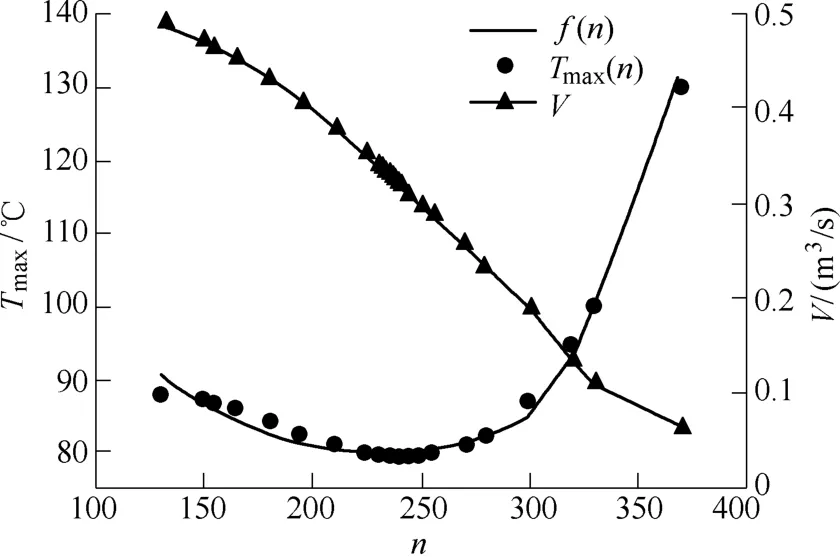
图4 散热器基板最高温度和单元风量随翅片数目n变化曲线Fig.4 Diagram of the maximum temperature of base plate and volume flow versus fin number

图4中实线f(n)表示曲线拟合函数，圆点Tmax(n)为仿真实验数据，带三角形标识的实线V为单元风量的变化情况。从图4可看出实验数据点基本上落在拟合曲线上，或者分散在拟合曲线附近且误差较小，说明拟合仿真f(n)与实验数据能够较好地吻合。

图4的仿真实验数据中，翅片数目n由130片开始增大，初始阶段时，Tmax(n)呈下降趋势，n继续增加到一定程度时，Tmax(n)转而上升。这是因为n较小时散热通道内风量较大，但是对流过程的散热面积也会随之减小，适当增大n可增加对流作用，但是n过大，系统的阻力会增大，导致风机压降增大和风量减少，单位时间内流过散热器翅片间的空气量减少，因而空气与翅片之间的热交换减少，使得Tmax(n)呈上升趋势。此外n增大还将使散热器的重量明显增加。因此在优化设计中应当选择合适的n值。

本文选取3.1节所述的多项式函数1, x, x2,…, xm为拟合基函数。通过取不同的m值，得出当m=3时，拟合多项式f (x)在实验样本点xi（i=1,2,…,28）处的函数值与实验样本点所对应的数据点yi偏差的二次方和最小，最终确定拟合多项式f(n)最高阶为三阶，函数表达式为

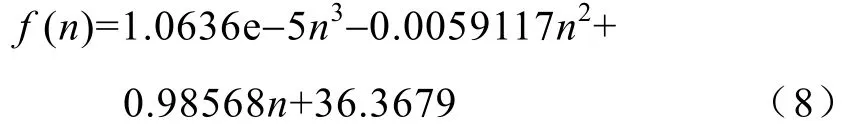
式（8）反映了应变量f(n)随自变量n的变化情况。求解d(f (n))/dn=0，得当n=243.88时存在f (n)的极小值点。当连续函数f (n)在n取值范围内仅有一个的极小值点时，该点对应的值为f (n)在该区间上的最小值。因为翅片数目只能为整数，对n值进行取整，由此可得当基板最高温度Tmax取最小值时对应的翅片数目为244片。

3.3 改变散热器基板厚度a

设定翅片数目n=244，散热器的基板厚度a分别为10mm、12mm、14mm、15mm、18mm和20mm时，得到仿真结果如图5所示。

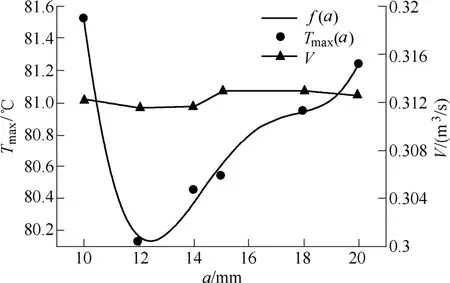
图5 散热器基板最高温度和单元风量随散热器基板厚度a变化曲线Fig.5 Diagram of the maximum temperature of base plate and volume flow versus thickness of base plate

图5中，实线f (a)表示曲线拟合的结果，圆点Tmax(a)为仿真实验数据，带三角形标识的实线V为单元风量的变化情况。

图5中，当散热器基板厚度a从20mm减小至12mm时，PEBB单元中Tmax(a)呈减少趋势，这是因为散热器基板厚度变薄可在一定程度上缩短热的传播路径，减小热阻并减少散热器上的热积累。而a从12mm减小到10mm，Tmax(a)却呈现上升趋势。根据式（7）分析可知，a值减少，散热器的热阻应该降低，基板温度也随之降低，但a值处于10～12mm区间内，散热器基板温度Tmax(a)却有所上升。这是因为式（7）的成立是以假设热源和散热器基板面积大小相同，翅片均为近端翅片为前提条件的，而对远端翅片（即远离热源与散热器基板接触面积的翅片）的问题未予以考虑。该区间内基板最高温度上升则是因为当基板过薄时，热源向远端翅片热扩散途径中的截面积减小，热阻变大，导致散热器上温度分布不均匀，最终使得单元的最高温度有所升高。通过曲线拟合得出描述图5所示现象的函数f(a)最高阶为四阶，其表达式为

求解d(f (a))/da=0，可得当a=12.4时该函数取值最小，因此在PEBB单元优化设计中a取值12.4mm左右为宜，为便于加工制作，散热器基板厚度a取12mm。另外，图5中PEBB单元的空气流量变化较小，最高温度变化范围不超过2℃，说明在固定散热器的翅片高度、厚度和数目的前提下，仅改变散热器基板厚度对系统流量、阻力和温度的影响并不明显。

综上所述，本文最终得到散热器结构参数的推荐值为：翅片数目n=244片，基板厚度a=12mm。

图6是优化后PEBB单元的散热器基板的温升分布。在系统的总功耗为3 932.76W的情况下，散热器基板上的最高温度为80.13℃，热阻为0.006 4K/W，芯片最高温度为99.06℃，两者均符合温度限制要求。

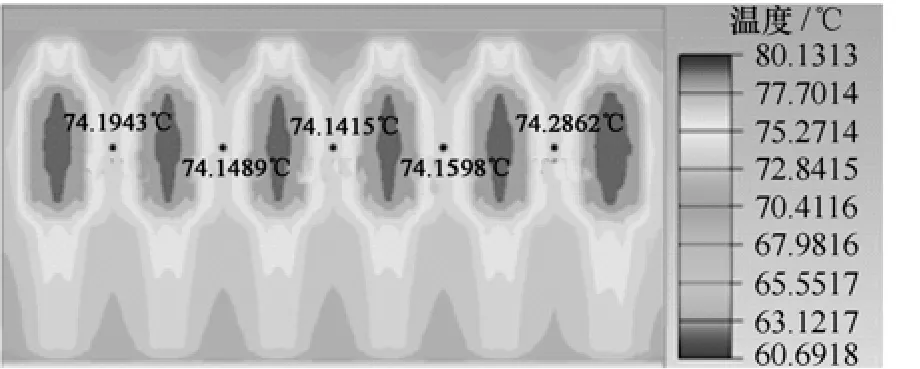
图6 优化后PEBB单元温度分布Fig.6 Temperature distribution of optimized PEBB unit

4 PEBB单元的温升测试实验

为验证本文方法的有效性，按照所得到的推荐值制作了一套PEBB单元，并对其进行了温升测试实验，实验装置如图7所示。实验采用TINKO公司生产的CTM系列接触式多通道测温仪器，该仪器采用的测温元件为PT100（铂热电阻），可交替显示多个测温点的温度，实现实时检测。待温度达到稳态时，采用电气及工业用红外热成像仪FLIRE50拍摄红外图像。

图7 实验样机测试照片Fig.7 Test photo of prototype

文中实验是在高温、恒温和恒湿实验箱中进行的，实测环境温度为54.3℃，IGBT模块的电流有效值Ic为105A。图8为温度达到稳定时实验装置的红外热成像。

图8 红外热成像Fig.8 Infrared imaging picture

由于驱动板供电回路的高频变压器功耗较大，图8中，最高温度点出现在IGBT模块的驱动板上，约为85℃。

由于IGBT底板下和IGBT模块内芯片结温的温度信号不易测得，因此本文仅测量图中打孔位置（即散热器基板上每两个IGBT模块的中间位置）的温度，测温点1为图7左起第一个孔，其余几个测温点从左到右依次排列，测温仪器通过引线于此处获得输出信号。测得实验温升，并与仿真所得的温升值进行对比，见表2。

表2 实验、仿真数据对比Tab.2 Comparison between experiment and simulation data

由表2可知，仿真数据与实际温升值的最大误差绝对值为1.05℃，最大相对误差约为5.2%。实验值均高于仿真值，这是由于软件采用有限容积法存在一定计算误差，实验测量也难免会引入误差，但两者均在允许范围之内。因此可看出，仿真数据对实际测量的结果具有较好的近似性，能够较为准确地反映一定功率情况下PEBB单元的散热情况。

5 结论

本文对PEBB单元中IGBT模块功率损耗进行了详细分析，通过适当简化，建立了包含IGBT模块和热管散热器的热仿真稳态数值模型，采用ICEPAK软件进行数值仿真，通过改变散热器参数得到大量的仿真数据，根据所得数据采用曲线拟合的方法求出各影响因子条件下的参数寻优函数，依据函数求解出散热器设计的最优值，为结构优化提供理论依据。最后，通过实验与仿真对比，证明了曲线拟合方法的有效性，采用该优化设计方法可使PEBB单元达到最佳散热效果，具有良好的工程应用价值。

参考文献

[1] 程启明, 程尹曼, 薛阳, 等. 三相电压源型PWM整流器控制方法的发展综述[J]. 电力系统保护与控制, 2012, 40(3): 145-155.

Cheng Qiming, Cheng Yinman, Xue Yang, et al. A summary of current control methods for three-phase voltage-source PWM rectifiers[J]. Power System Protection and Control, 2012, 40(3): 145-155.

[2] 王红玲, 张元敏, 方波. 基于CPWM控制方式的正弦波逆变器电路设计[J]. 电力系统保护与控制, 2009, 37(2): 76-79.

Wang Hongling, Zhang Yuanmin, Fang Bo. Design of sine-wave inverter based on CPWM control model[J]. Power System Protection and Control, 2009, 37(2): 76-79.

[3] 陈明, 胡安, 刘宾礼, 等. 绝缘栅双极型晶体管失效机理与寿命预测模型分析[J]. 西安交通大学学报, 2011, 45(10): 65-71.

Chen Ming, Hu An, Liu Binli, et al. Failure mechanism and lifetime prediction modeling of IGBT power electronic devices[J]. Journal of Xi'an Jiaotong University, 2011, 45(10): 65-71.

[4] 刘德红, 王向军, 嵇斗, 等. 基于钎焊技术的大功率PEBB散热器性能分析[J]. 电力电子技术, 2013, 47(2): 41-43.

Liu Dehong, Wang Xiangjun, Ji Dou, et al. Thermal performance analysis of high power PEBB heatsink based on vacuum brazed technique[J]. Power Electronics, 2013, 47(2): 41-43.

[5] 张明元, 沈建清, 李卫超, 等. 一种快速IGBT损耗计算方法[J].船电技术, 2009, 29(1): 33-36.

Zhang Mingyuan, Shen Jianqing, Li Weichao, et al. Calculation method of a fast power loss for IGBT modules[J]. Marine Electric & Electronic Technology, 2009, 29(1): 33-36.

[6] 胡建辉, 李锦庚, 邹继斌, 等. 变频器中的IGBT模块损耗计算及散热系统设计[J]. 电工技术学报, 2009, 24(3): 159-163.

Hu Jianhui, Li Jingeng, Zou Jibin, et al. Losses calculation of IGBT module and heat dissipation system design of inverters[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 159-163.

[7] 刘建涛, 王治华, 王珂. 不同结构电压源换流器损耗对比分析[J]. 电力系统保护与控制, 2013, 41(6): 105-110.

Liu Jiantao, Wang Zhihua, Wang Ke. Comparative analysis of losses of voltage source converters with different structures[J]. Power System Protection and Control, 2013, 41(6): 105-110.

[8] 朱艺锋, 葛琼璇, 刘育红, 等. 75kVA三电平背靠背变流器的散热分析及优化[J]. 电工技术学报, 2012, 27(2): 103-108.

Zhu Yifeng, Ge Qiongxuan, Liu Yuhong, et al. Analysis and optimization of cooling system for 75kVA three-level back-back converter[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 103-108.

[9] 杜毅, 廖美英. 逆变器中IGBT模块的损耗计算及其散热系统设计[J]. 电气传动自动化, 2011, 33(1): 42-46.

Du Yi, Liao Meiying. Losses calculation of IGBT module and heat dissipation system design of inverters[J]. Electrical Drive Automation, 2011, 33(1): 42-46.

[10] 付桂翠, 高泽溪. 影响功率器件散热器散热性能的几何因素分析[J]. 电子器件, 2003, 26(4): 354-356, 460.

Fu Guicui, Gao Zexi. Analysis of geometric factors on effect upon the capability of heat sink of power component[J]. Chinese Journal of Electron Devices, 2003, 26(4): 354-356, 460.

[11] 刘玉芬, 程洪亮. 变频器的热耗计算及散热分析[J].电气制造, 2008, 8(3): 60-62.

Liu Yufen, Cheng Hongliang. Power loss calculation and heat dissipation analysis of inverters[J]. Electrical Manufacturing, 2008, 8(3): 60-62.

[12] 李文顶, 莫锦秋, 曹家勇. 中压矿用变频器主电路损耗分析及散热设计[J]. 机电工程技术, 2009, 38(7): 85-87, 181.

Li Wending, Mo Jinqiu, Cao Jiayong. Loss analysis and thermal design of mid voltage & mine-used inverter main circuit[J]. Mechanical & Electrical Engineering Technology, 2009, 38(7): 85-87, 181.

[13] Xu D W, Lu H W, Huang L P, et al. Power loss and junction temperature analysis of power semiconductor devices[J]. IEEE Transactions on Industry Applications, 2002, 38(5): 1426-1431.

[14] 谭国俊, 景巍. 有源钳位三电平变频器及其结温平衡控制[J]. 电工技术学报, 2012, 27(2): 97-102.

Tan Guojun, Jing Wei. Active neutral point clamped three-level converter and its junction temperature balancing control[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 97-102.

[15] Casanellas F. Losses in PWM inverters using IGBTs[J]. IEE Proceedings-Electric Power Applications, 1994, 141(5): 235-239.

[16] 王群京, 陈权, 姜卫东, 等. 中点钳位型三电平逆变器通态损耗分析[J]. 电工技术学报, 2007, 22(3): 66-71, 90.

Wang Qunjing, Chen Quan, Jiang Weidong, et al. Analysis of conduction losses in neutral-point-clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2007, 22(3): 66-71, 90.

[17] 杨世铭, 陶文铨. 传热学[M]. 西安: 西北工业大学出版社, 2006.

[18] 诸凯, 李媛媛, 陆佩强, 等. 高性能热管散热器的实验研究与数值模拟[J]. 工程热物理学报, 2010, 31(11): 1945-1947.

Zhu Kai, Li Yuanyuan, Lu Peiqiang, et al. Experimental study and numerical simulation of high performance heat pipe radiator[J]. Journal of Engineering Thermophysics, 2010, 31(11): 1945-1947.

[19] 刘一兵. 功率器件散热技术的研究[J]. 湖南工业大学学报, 2007, 21(4): 77-79.

Liu Yibing. Research on heat dissipation technology for power device[J]. Journal of Hunan University of Technology, 2007, 21(4): 77-79.

[20] 揭贵生, 孙驰, 汪光森, 等. 大容量电力电子装置中板式水冷散热器的优化设计[J]. 机械工程学报, 2010, 46(2): 99-105.

Jie Guisheng, Sun Chi, Wang Guangsen, et al. Optimization design of water-cooled heat sink applied to large-capacity power electronic equipment[J]. Journal of Mechanical Engineering, 2010, 46(2): 99-105.

[21] 赵臣烜, 张珏, 张言安. 基于ICEPAK的散热器优化设计[J]. 机械工程师, 2013, 29(6): 124-126.

Zhao Chenxuan, Zhang Jue, Zhang Yanan. The optimum thermal design of heat sink based on ICEPAK[J]. Mechanical Engineer, 2013, 29(6): 124-126.

[22] Ning P, Lei G, Wang F, et al. Selection of heatsink and fan for high-temperature power modules under weight constraint[C]//IEEE Applied Power Electronics Conference and Exposition, 2008: 192-198.

陈国栋 男，1982年出生，博士，工程师，研究方向为电能质量控制技术和大功率电力电子变换技术。

E-mail: chengd@shanghai-electric.com（通信作者）

刘 宏 女，1987年生，硕士，工程师，研究方向为电力电子器件的散热设计和电力电子设备的冷却系统设计。

E-mail: liuhong2@shanghai-electric.com

作者简介

收稿日期2013-12-13 改稿日期 2015-05-29

中图分类号：TM464