高压架空导线径向热路模型及其参数计算方法

应展烽杜志佳冯 凯柳亚芳吴军基（. 南京理工大学能源与动力工程学院 南京 0094 . 国家电网南京供电公司 南京 009）



高压架空导线径向热路模型及其参数计算方法

应展烽1杜志佳2冯 凯1柳亚芳1吴军基1
（1. 南京理工大学能源与动力工程学院 南京 210094 2. 国家电网南京供电公司 南京 210019）

摘要为计算不同载流时的高压架空导线径向温度，利用径向热平衡原理，提出了基于状态方程形式的径向温度热路模型。根据几何分析，提出了径向环状截面内导线的热功率及热容计算方法。通过线性回归方法，对模型中不同截面内导线的径向热阻进行了灰箱辨识。为验证模型准确度，设计了径向温度梯度测量的实验平台，在实验室内对加载不同电流情况下的导线径向温度进行了实测。通过Simulink对径向热路模型进行了仿真，仿真与实验结果的对比表明，自然对流条件下，热路模型平均误差小于3.16%，能够用于计算不同电流时的导线径向温度梯度。

关键词：高压架空导线 热路模型 径向温度梯度 灰箱辨识

江苏省电力公司创新科技项目资助（2011LY226090425）。

Radial Thermal Circuit Model and Parameter Calculation Method for High Voltage Overhead Transmission Line

Ying Zhanfeng1Du Zhijia2Feng Kai1Liu Yafang1Wu Junji1
（1. School of Energy and Power Engineering Nanjing University of Science and Technology Nanjing 210094 China 2. State Grid Nanjing Power Supply Company Nanjing 210094 China）

Abstract To calculate current-radial temperature of high voltage overhead transmission line, a radial temperature thermal circuit model in the form of state equation was developed with the thermal equilibrium principle. A calculation method was proposed to estimate the heat flux and heat capacity of conductor on the transmission line radial annular cross section. With linear regression method, the radial thermal resistance of thermal circuit model was obtained by grey box identification. To validate the reliability of model, an experiment was designed to measure the radial temperatures of transmission line with various current. A simulation with thermal circuit model was performed to calculate the radial temperature by Simulink. Comparing the experiment and simulation, the average relative error of proposed thermal circuit model is less than 3.16% in natural convection. The results indicate that the proposed thermal circuit model has potential application applied in radial temperature gradient calculation of transmission line with various current.

Keywords：High voltage overhead transmission line, thermal circuit model, radial temperature gradient, grey box identification

0 引言

高压架空导线温度是电力系统安全运行和输电线路设计改造的重要指标。当前工程上通用的导线电流与运行温度关系计算模型已形成了标准[1]，能够为导线增容[2,3]、弧垂张力计算[4]、电热协调潮流分析[5,6]等技术供实时温度数据。标准模型建立在热平衡原理上，且假设导线为等温体。事实上因对流换热的冷却作用，导线表面温度低于内部温度，存在径向温度梯度。

工程中，导线径向温度长期以来被忽略。大部分情况下，由于导线直径远小于档距，材料导热系数较高，这种忽略可以接受。但相关实验表明，导线径向温度差异随环境风速及电流的提高而加剧[7]，恶劣条件下导线内外温差可达5℃～15℃或更高。此时若仍将导线视为等温体，利用表面温度来计算线路输电载流裕量或弧垂，将会低估线路运行的安全性，增加运行风险[8]。此外，研究还表明：导线覆冰融冰模型、蠕变退火过程均与径向温度梯度相关[9,10]。故径向温度计算有助于深度揭示外部环境和自身发热对导线运行状态影响的机理，对高压输电系统状态监测及故障诊断技术发展具有重要意义。

目前已有针对导线电流与径向温度关系的计算模型[9-11]，但模型普遍建立在传热学和流体力学基础上，多数通过有限元方法实现。然而限元方法准确度依赖于计算网格尺寸和结构的划分，计算量大、使用不便。近年来，凭借计算量小，可反映温升暂态过程等优势，热路模型[12-20]被应用于包括架空导线在内的各类电力设备热动态分析中。该模型基于热电类比理论，通过Simulink即可仿真相关温度，计算量小、准确度高。但针对架空导线的热路模型仍处于发展阶段，无法计算导线径向温度梯度。

本文建立了用于计算不同电流时导线径向温度梯度的热路模型，提出了热路参数的计算方法。为验证模型准确度，搭建了实验平台，在自然对流条件下，对导线径向温度进行了实测。实验与仿真结果对比验证了模型有效性。

1 导线径向温度热平衡原理

当整段导线处所的散热环境相同时，轴向温差较小，径向温度梯度大，故可视为一维传热问题。用m条半径以Δr值递增的圆形分割曲线将架空导线总截面划分为如图1所示的m个环状截面Zi， i∈[1,m]，根据传热学原理[21]，不考虑日照吸热，每个截面Zi的热平衡方程为

式中，t为时间；mi、ci、Ti和QJi分别代表处于截面Zi内导线的质量、比热容、温度及因电流产生的热功率；QD(i-1)为截面Zi-1内导线向截面Zi内导线传导的热流量；QDi为截面Zi内导线向截面Zi+1内导线传导的热流量；Qc为表面因对流损失的热流量。

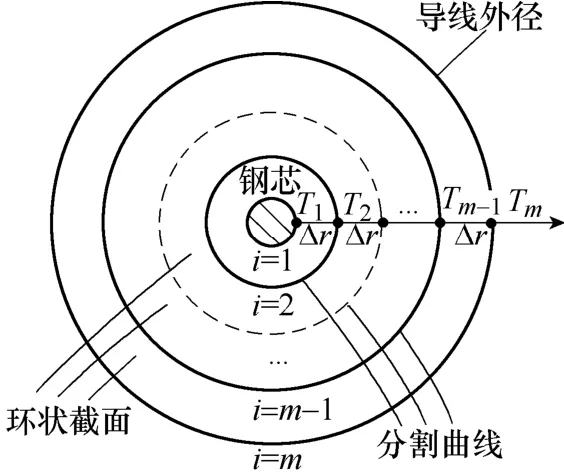
图1 导线环状截面划分示意图Fig.1 The schematic diagram of transmission line annular cross section

考虑到对于架空导线材料而言，温度在150℃～200℃以下时，对流换热起主导作用，辐射换热影响相对较小[22]，故式（1）中忽略了辐射换热项。

根据傅里叶定律和牛顿冷却公式，热传导和对流换热的热流量可表达为

式中，λi和Si为截面Zi的导热系数和截面积；hc为对流换热系数；A为对流换热面积；TE为环境温度。

2 径向温度梯度的热路模型

由式（1）和式（2）可推得

式中，Ci为截面Zi中的导线热容

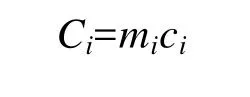
Ri为截面Zi中导线的导热热阻及对流热阻

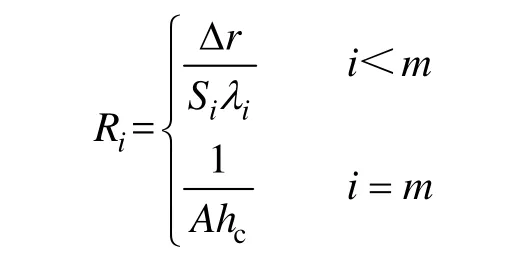
式（3）即被称为热路模型，可反映导线电流和径向温度的关系，图2为模型示意图。至此，传热问题转化为了一个多输入多输出的m阶线性系统计算问题。

图2 导线径向热路模型Fig.2 The transmission line radial thermal circuit model

环境温度TE相当于在各节点温度初值上叠加了一个直流分量，为简化运算，可将其从模型中去除，各节点温度初值为0。根据线性系统理论，这种处理不影响系统动态特性。此时热路模型可写为状态方程形式

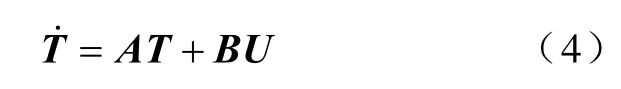
其中

矩阵A中，对于元素aij，当i=1时有

当1＜i＜m时，有

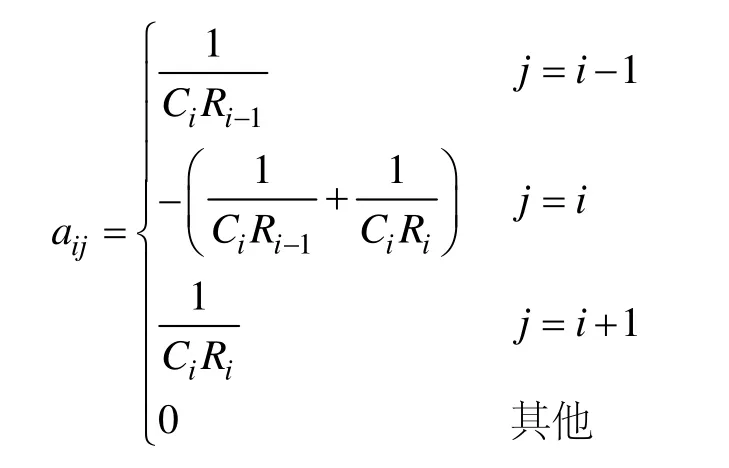
当i=m时，有

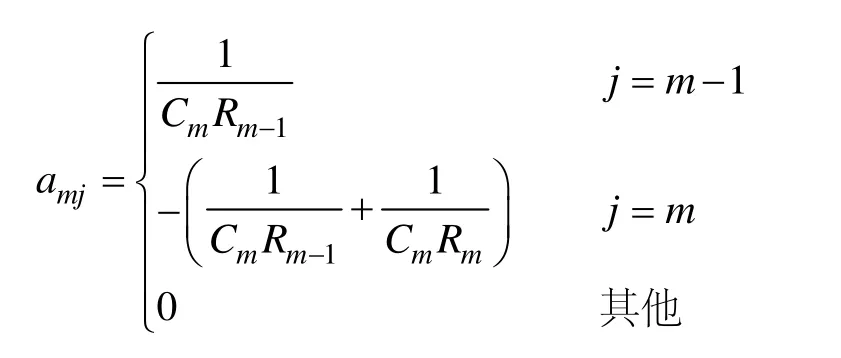
在获知模型参数的情况下，利用Simulink可仿真热路模型，得到径向各点温度计算值。

3 环状截面中的导线热功率和热容参数计算

为求不同截面Zi中导线的热功率和热容参数，必须先分析Zi中所包含的钢芯或铝线截面大小。

以LGJ—400/35导线为例，其规格参数来源于文献[23]。该导线由五层线束绞绕。本文将每层线束中的单根钢芯或铝线称为单股导线，并设导线加工工艺良好，单股导线截面均为规则圆形。图3为第j层线束排列示意图，设该层线束由K条单股导线组成，顺时针方向编号，rj,k为第k条单股导线直径，φ为相邻的两条单股导线圆心相对坐标原点之间的夹角，lj,k为第k条单股导线圆心相对坐标原点的距离。通过几何运算可知第j层第k根单股导线截面圆的坐标公式为

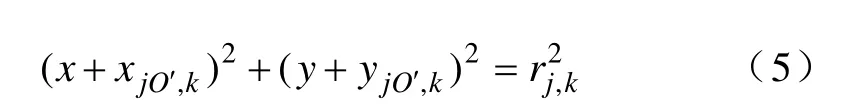
式中，(xjO', k,yjO', k)为单股导线截面圆原点O'j, k坐标，O'j, k均匀分布在以原点为圆心，以lj, k为半径的圆上，故易得

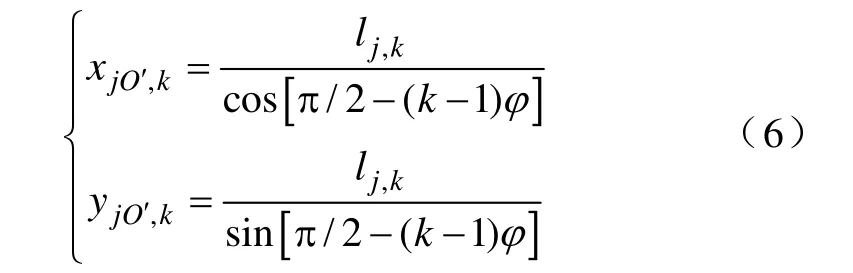
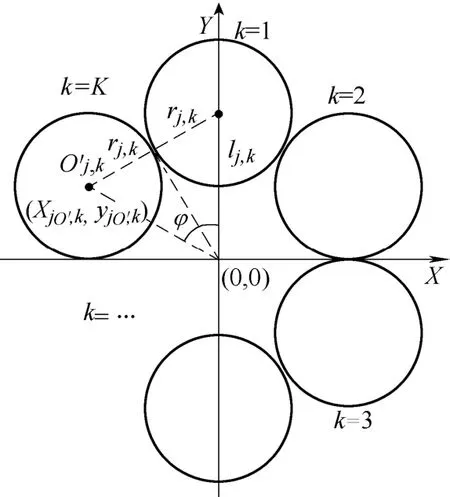
图3 导线第j层线束排列Fig.3 Transmission line conductor array in the j layer

其中

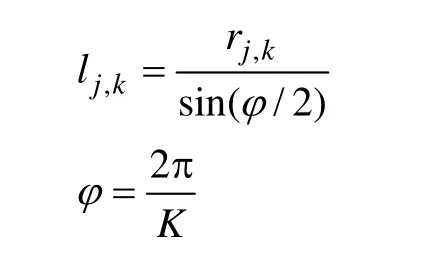
设第i条圆形分割曲线用符号Vi表示，则其坐标为

由图1易知，环形截面Zi是由曲线Vi和Vi+1分割导线而成的。若Zi中一共包含了N条单股导线的全部或部分截面，设其中第n条单股导线半径为ri,n，被Zi包含的截面称为Xi,n。根据分割曲线与单股导线截面圆交点形式的不同，Xi,n存在如图4所示的8种形式。图中深色部分即表示截面Xi,n，O和O'点分别代表分割曲线及单股导线的原点。A、B点代表分割曲线Vi+1与单股导线截面圆的交点，C、D点代表分割曲线Vi与单股导线截面圆的交点。E和E'点分别代表线段LAB和LCD的中点。表1列出了这8种截面Xi,n的数学特征描述。结合数学特征描述和交点形式可区分这8种截面。

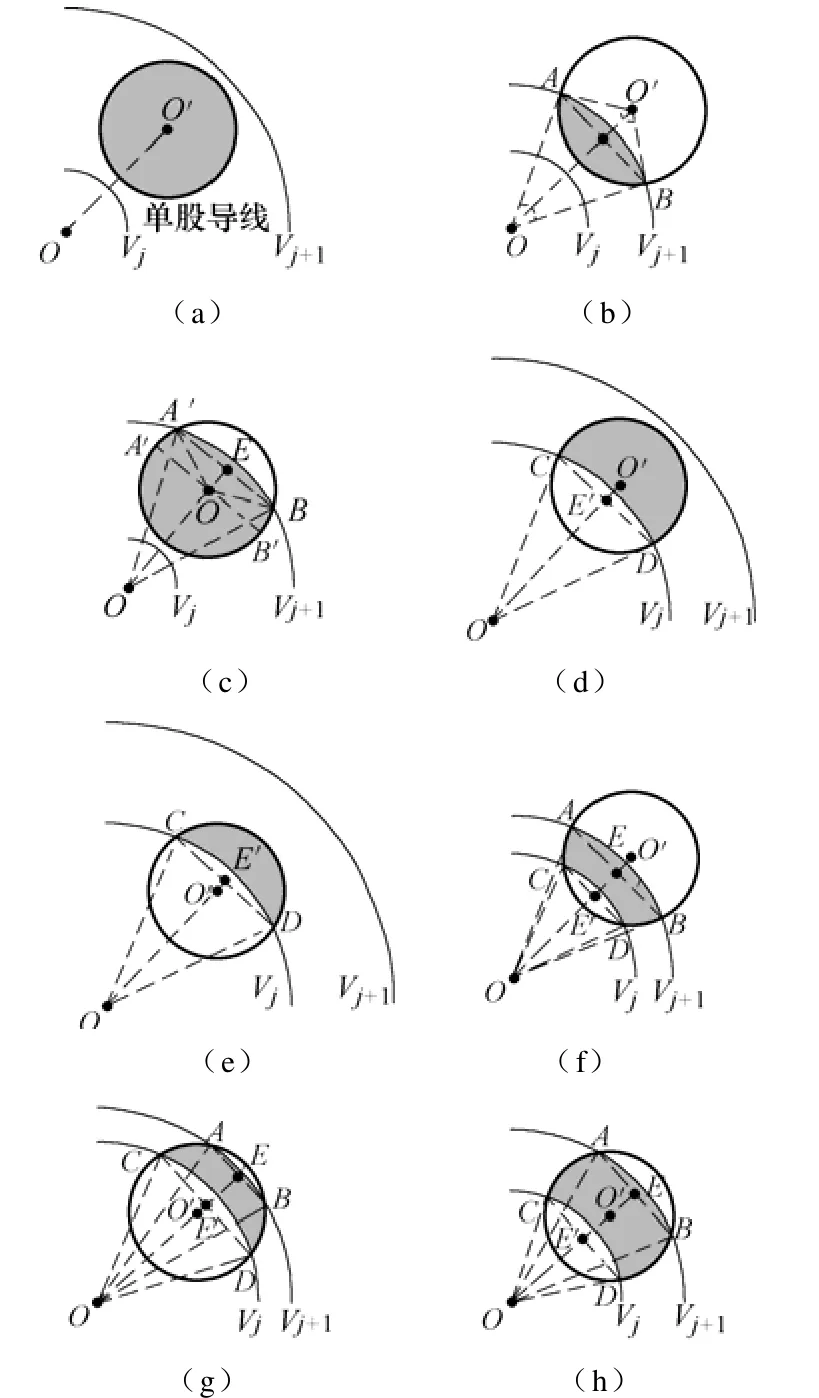
图4 Xi,n截面的8种形式Fig.4 Eight kinds of cross section Xi,n

表1 截面Xi,n的8种形式特征描述Tab.1 Mathematical description of eight kinds of cross section

设图4中的8种Xi,n面积分别表示为w∈ [1,8]。容易发现，图4a的Xi,n面积等于单股导线面积，即

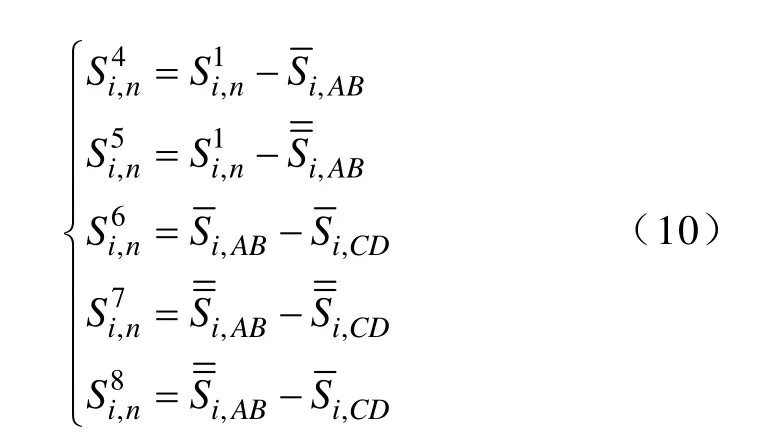
在图4b中，通过几何分析，有

在图4c中，过点O'做平行于AB的直线，交单股导线截面圆与A'和B'点，则

通过式（6）可得O'坐标，联立式（5）和式（7）可得交点A、B、C、D坐标，进而得到E、E'、A'、B'点坐标。此时式（11）和式（12）中的所有扇形、三角形面积均可求解，故和可解。再利用式（8）～式（10）可求得被Zi包含的单股导线截面Xi,n的面积Si,n。

忽略趋肤效应，根据电阻的定义，截面Zi中导线的等效电阻Ωi和整段导线的电阻Ω为式中，L为实验导线的长度，σi,n为Zi截面包含的第n条单股导线电阻率，其值与温度有关，修正方法可参考文献[26]。

根据热功率和热容的定义，截面Zi中导线的QJi和Ci参数按如下公式计算。

式中，I为导线通过的电流；ρi,n和ci,n分别为截面Zi包含的第n条单股导线的密度和比热容。

4 热阻的参数辨识

钢芯铝绞导线由多股钢芯和铝线互绞而成，导线内部存在空隙，存在接触热阻，理论计算困难，故热阻Ri应采用灰箱参数辨识方法计算。式（4）表明待辨识的状态方程参数存在耦合关系，通过线性回归算法[24,25]可实现辨识。

令k时刻第i个截面的导线温度为k∈n，将式（4）按时间离散后，得，[0,]

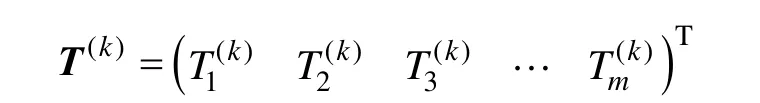
有

其中

H阵中，P(k)阵可表示为

对于元素()

p，当i=1时有

k

ij

当1＜i＜m时，有

当i=m时，有

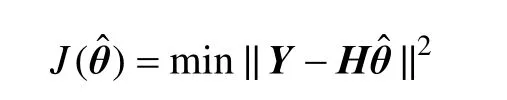
约束条件为：θ1≥1，θ2≥0，θ3≥0，θ4≥0。求得后，即得热阻Ri，完成参数辨识。

5 热路模型的实验验证

5.1 实验设计

为验证热路模型的准确度，设计了图5所示的高压架空导线径向温度梯度测量实验平台。实验平台由钢架、实验导线、大电流发生器、电流互感器、数采装置和PC构成。

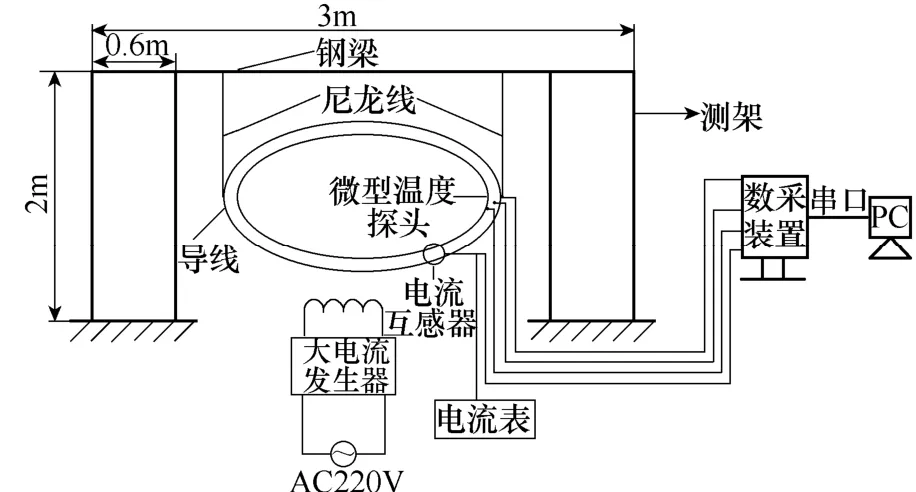
图5 导线径向温度梯度测量实验平台Fig.5 Experimental plate for transmission line radial temperature gradient

实验钢架由两个侧架及一根钢梁构成，起支撑作用。钢梁两侧安装有高强度尼龙细线，用于悬挂实验导线。实验导线采用LGJ—400/35钢芯铝绞裸导线，长5.5m。导线上装有电流互感器，互感器有两路输出，一路给数采装置，一路给电流表现场显示。实验时，大电流发生器将电流耦合至实验导线。数采装置通过微型温度探头采集导线各测量点的温度，并将数据通过串口上传至PC的数据库中。

导线径向温度采用文献[26,27]的钻孔方法测量。共设有三个测量点，分别位于导线钢芯，铝层中心及导线表面。从径向上观察，该三个点数据可反映导线径向温度梯度。

实验平台被安置在5m×4m×3m实验室中，室内空气流速小于0.1m/s，属自然对流。实验阶段，室内温度和湿度分别为21℃和60%HR，变化范围分别不超过±0.5℃和1%HR，近似为恒温恒湿环境。

5.2 实验结果分析

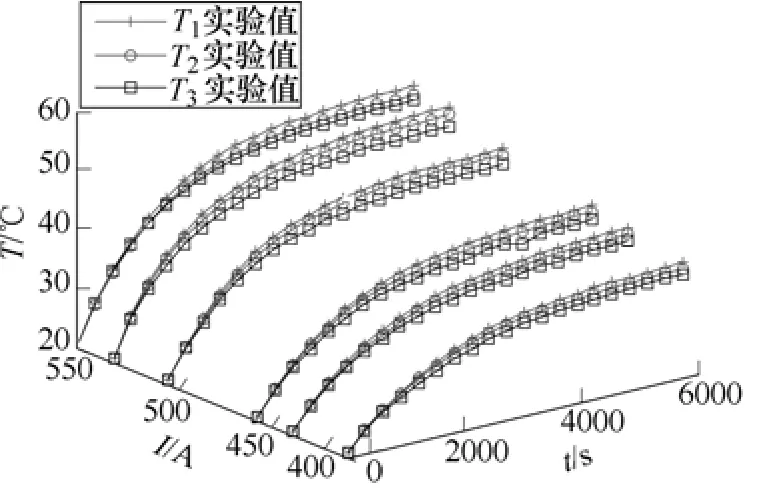
图6 不同电流条件下各测量点实验结果Fig.6 Experiment results of measurement point with various current

实验平台导线上加载不同电流，每次实验时长为100min。导线测量点i=1,2,3的实验温升T1、T2、T3曲线如图6所示。表2列出了不同电流条件下实验末段1min内的平均温度，此时温度基本处于稳态。分析可见，由于表面对流换热冷却作用，导线出现径向温度梯度。实验末段，线芯温度明显高于表面温度，且温差随着电流的提高呈增加趋势。

表2 不同电流条件下各测量点稳态温度Tab.2 Experimental steady-state temperature of measurement point with various current

5.3 径向热路模型验证

利用式（13）计算得到各测量点所在截面的导线热容分别为C1=590J/K，C2=1 762.5J/K，C3= 2 971.5J/K，不同电流时各测量点所在截面的导线热功率见表3。利用式（14）得到各测量点平均热阻为

R1=0.100 3K/W

R2=0.037 6K/W

R3=0.224 3K/W

表3 不同电流条件下各测量点所在截面的导线热功率Tab.3 Thermal power of conductor in cross section of measurement point with various current

利用Simulink对热路模型仿真，得到不同电流时的导线动态温升仿真结果如图7所示，图8为仿

图7 不同电流条件下各测量点仿真结果Fig.7 Simulate results of measurement point with various current

图8 不同电流条件下仿真结果误差Fig.8 Relative errors of simulate result with various current

真与实验结果的对比误差曲线。表4列出了仿真结果的平均相对误差。

表4 仿真结果的平均相对误差Tab.4 The average relative errors of simulate results

数据表明自然对流条件下，热路模型仿真结果平均相对误差小于3.16%。上述误差由主要三方面原因导致。①实验温度探头存在固有测量误差，影响热阻辨识准确度；②忽略了环形截面中单股导线的趋肤效应，截面参数估算存在一定误差；③忽略了辐射换热影响，虽然其不起主导作用，但仍可能导致少许误差。尽管存在上述原因，本文热路模型仍具有较高准确度。

利用Ansys中的有限元方法在同等条件下对导线径向温度进行仿真。导线沿径向同样划分为三层环状截面。图9为电流400A时，在仿真末段时刻下的导线径向稳态温度分布云图。不同电流时稳态仿真结果平均误差见表5。分析可见，有限元得到的线芯温度亦高于表面温度，但温差却较小，与实验结果不吻合。另外，仿真结果误差相对较大。这是由于架空导线钢芯和铝线互绞时存在间隙，间隙内空气和导体表面粗糙度产生接触热阻，影响径向传热过程和温度分布。有限元计算准确度与其划分的网格尺寸相关，当导线沿径向划分的环状截面较大时，有限元将截面内材料视为热的良导体，无法反映接触热阻对传热的影响，故计算准确度较低，且不能真实表现导线线芯与表面温差。为提高准确度，有限元法要求网格尺寸应远小于各股导线之间的微小间隙，加入接触热阻影响，并严格按照真实导线结构和形状划分网格，这将极大增加计算量和复杂度。而热路模型中，接触热阻包含在辨识得到的热阻参数中，无需另外计算，且不受划分后导线环状截面尺寸影响。离线方式对导线参数辨识后，通过Simulink仿真即可在线计算径向温度梯度，使用方便。故相对有限元方法，本文模型工程实用性更高。

图9 400A时有限元仿真温度云图Fig.9 The temperature field cloud picture of finite element simulation with 400A

表5 不同载流时有限元仿真稳态结果平均误差Tab.5 The average errors of finite element simulation steady-state results with various current

需说明的是，实际架空线路所处的环境条件复杂，还存在风和日照辐射等影响。风可改变对流热阻参数，日照辐射则影响热路模型中的热源。本文研究虽然在无日照的自然对流条件下进行，但所建立的热路模型及其参数计算方法却是研究强迫对流和日照辐射条件下导线径向温度分布的重要基础和前提条件，可为电力调度和线路设计人员提供一种更为安全、保守的导线温度算法，也能为架空线路覆冰、融冰、蠕变退火等模型的深入研究提供径向温度计算方法。

6 结论

本文提出了高压架空导线径向温度热路模型和模型参数的计算方法。设计了导线径向温度梯度实验平台，对导线径向温度进行了实测，实验结果与计算结果表明：

1）导线径向存在温度梯度，线芯温度明显高于导线表面温度，且温差随载流量的提高呈增大趋势。

2）自然对流下，导线径向温度热路模型仿真结果平均相对误差小于3.16%，能够用于计算不同载流时的导线径向温度梯度。

3）径向热路模型的热阻通过辨识得到，不受划分后的导线环状截面尺寸影响，可获得较高计算准确度，相对有限元方法，本文模型工程实用性更高。

参考文献

[1] IEEE Std 738—2006, IEEE standard for calculating the current-temperature of bare overhead conductors [S].

[2] 黄新波, 孙钦东, 张冠军, 等. 输电线路实时增容技术的理论计算与应用研究[J]. 高电压技术, 2008, 34(6): 1138-1144. Huang Xinbo, Sun Qindong, Zhang Guanjun, et al. Theoretical calculation and capacity-increase application study on real-time of transmission lines[J]. High Voltage Engineering, 2008, 34(6): 1138-1144.

[3] 马晓明, 范春菊, 胡天强, 等. 基于热稳定约束的架空导线增容计算研究[J]. 电力系统保护与控制, 2012, 40(14): 86-91. Ma Xiaoming, Fan Chunju, Hu Tianqiang, et al. Calculation of current carrying capacity of overhead transmission line based on thermal stability constraint [J]. Power System Protection and Control, 2012, 40(14): 86-91.

[4] Mehran K, Charles H P. Sag and tension calculations for overhead transmission lines at high temperatures—modified ruling span method[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 777-783.

[5] 董晓明, 梁军, 韩学山, 等. 计及输电线路温度变化的连续潮流模型与计算[J]. 电力系统保护与控制, 2012, 40(23): 36-41. Dong Xiaoming, Liang Jun, Han Xueshan, et al. Model and calculation of continuation power flow considering change of transmission line temperature [J]. Power System Protection and Control, 2012, 40(23): 36-41.

[6] Banakar H, Alguacil N, Galiana F D．Electrothermal coordination. part I: theory and implementation scheme[J]．IEEE Transactions on Power Systems, 2005, 20(2): 798-805.

[7] Shelley L C, William Z B, Michael L F. Hightemperature sag model for overhead conductors[J]. IEEE Transactions on Power Delivery, 2003, 18(1): 183-188.

[8] Black W Z, Collins S S. Theoretical model for tempurature gradients within bare overhead conductors[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 707-715.

[9] Fan Songhai, Jiang Xingliang, Shu Lichun, et, al. DC ice-melting model for elliptic glaze iced conductor[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2697-2703.

[10] Morgan V T. The radial temperature distribution and effective radial thermal conductivity in bare solid and stranded conductors[J]. IEEE Transactions on Power Delivery, 1990, 3(5): 1443-1452.

[11] Minambres J F, Barandiaran J J, Alvarez Isasi R, et al. Radial temperature distribution in ACSR conductors applying finite elements[J]. IEEE Transcations on Power Delivery, 1999, 14(2): 472-480.

[12] Shenkman A L, Chertkov M. Experimental method for synthesis of generalized thermal circuit of polyphase induction motors[J]. IEEE Transactions on Energy Conversion, 2000, 15(3): 264-268.

[13] Kun Z, Ming C C. Thermal circuit for SOI MOSFET structure accounting for nonisothermal effects[J]. IEEE Transactions on Electronic Devices, 2010, 57(11): 2838-2847.

[14] Zoran R, Kurt F. A new method for the calculation of the hot-spot temperature in power transformers with ONAN cooling[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1284-1292.

[15] 景巍, 谭国俊, 叶宗彬. 大功率三电平变频器损耗计算及散热分析[J]. 电工技术学报, 2011, 26(2): 134-140. Jing Wei, Tan Guojun, Ye Zongbin. Losses calculation and heat dissipation analysis of high-power threelevel converters[J]. Transactions of China Electrotechnical Society, 2011, 26(2): 134-140.

[16] 白保东, 陈德志, 王鑫博. 逆变器IGBT损耗计算及冷却装置设计[J]. 电工技术学报, 2013, 28(8): 97-106. Bai Baodong, Chen Dezhi, Wang Xinbo. Loss calcula-tion of inverter IGBT and design of cooling device[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 97-106.

[17] 胡建辉, 李锦庚, 邹继斌, 等. 变频器中的IGBT模块损耗计算及散热系统设计[J]. 电工技术学报, 2009, 24(3): 159-163. Hu Jianhui, Li Jingeng, Zou Jibin, et al. Losses calculation of IGBT module and heat dissipation system design of inverters[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 159-163.

[18] 刘刚, 阮班义, 张鸣. 架空导线动态增容的热路法暂态模型[J]. 电力系统自动化, 2012, 36(16): 58-63. Liu Gang, Ruan Banyi, Zhang Ming. A transient model for overhead transmission line dynamic rating based on thermal circuit method[J]. Automation of Electric Power Systems, 2012, 36(16): 58-63.

[19] 刘刚, 阮班义, 林杰, 等. 架空导线动态增容的热路法稳态模型[J]. 高电压技术, 2013, 39(5): 1107-1113. Liu Gang, Ruan Banyi, Lin Jie, et al. Steady-state model of thermal circuit method for dynamic overhead lines rating[J]. High Voltage Engineering, 2013, 39(5): 1107-1113.

[20] 林杰, 刘刚, 张海鹏, 等. 架空线路并沟线夹温度分布研究[J]. 电力系统保护与控制, 2013, 41(24): 88-94. Lin Jie, Liu Gang, Zhang Haipeng, et al. Research of temperature distribution of overhead lines parallel groove clamp[J]. Power System Protection and Control, 2013, 41(24): 88-94.

[21] 陶文铨. 传热学[M]. 西安: 西北工业大学出版社, 2006.

[22] Emmanuel I K, Panagiotis T T, John S K, et al. A wildfire model for the estimation of the temperature rise of an overhead line conductor[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 1077-1082.

[23] 李秀中. 电线电缆常用数据速查手册[M]. 北京: 中国电力出版社, 2010.

[24] Elias M. Local linear regression estimation under long-range dependence: strong consistency and rates [J]. IEEE Transactions on Information Theory, 2001, 47(7): 2863-2874.

[25] Franck D, Jean C N. Formulating robust linear regression estimation as a one-class LDA criterion: discriminative hat matrix[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(2): 262-273.

[26] Chen S L, Black W Z, Loard H W. High-temperature ampacity model for overhead conductors[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 1136-1141.

[27] Hall J F, Deb A K. Wind tunnel studies of transmission line conductor temperature[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 801-812.

应展烽 男，1982年生，博士，讲师，高压架空输电线路状态监测及电气设备电热耦合特性研究。

E-mail: yingzhanfeng@163.com（通信作者）

杜志佳 男，1986年生，硕士研究生，研究方向为高压架空输电线路状态监测技术。

E-mail: Duzhijia@163.com

作者简介

收稿日期2014-02-13 改稿日期 2014-05-26

中图分类号：TM751