考虑大地影响高速铁路轨道电路互阻抗快速计算简化公式

杜学龙王智新邹 军（. 清华大学电机系 北京 00084 . 北京全路通信信号研究设计院 北京 00073）



考虑大地影响高速铁路轨道电路互阻抗快速计算简化公式

杜学龙1王智新2邹 军1
（1. 清华大学电机系 北京 100084 2. 北京全路通信信号研究设计院 北京 100073）

摘要相邻轨道电路互阻抗是轨道电路计算分析的重要参数之一。考虑大地影响，推导了相邻轨道电路互阻抗简化表达式。根据Deri地阻抗表达式，获得两个相邻轨道电路之间的互阻抗；考虑轨道电路空间位置特点，采用泰勒公式对相邻轨道电路互阻抗表达式进行化简，得到一种快速计算公式。数值计算结果表明，化简后的相邻轨道互阻抗计算公式准确度高，可方便计算考虑大地情况下相邻轨道电路互阻抗。

关键词：高速铁路 轨道电路 互阻抗

A Fast and Simplified Formula for Calculating the Mutual Impedance with the Earth Return of the High-Speed Railway Track Circuit

Du Xuelong1Wang Zhixin2Zou Jun1
（1. Electrical Engineering Department Tsinghua University Beijing 100084 China 2. Beijing National Railway Research & Design Institute of Signal & Communication Beijing 100073 China）

Abstract The mutual impedance of two adjacent track circuits is one of the important parameters for analyzing the track circuit. Considering the earth return of the high-speed railway track circuit, a fast and simplified formula for calculating the mutual impedance is studied in this paper. First, the mutual impedance of two adjacent track circuits is obtained based on the Deri’s ground impedance expression. Then, according to the spatial location characteristics of track circuit, the expression of the mutual impedance is simplified through Taylor formula. The results indicate that the simplified formula has high accuracy, and is suitable for calculating the mutual impedance with the earth return of two adjacent track circuits.

Keywords：High-speed railway, track circuit, mutual impedance

0 引言

轨道电路是保证高速铁路稳定运行的重要技术之一[1-6]，轨道互阻抗是轨道电路计算的重要参数[7-9]。对于客运专线四对线路并行运行情况，相邻线路同频信号会通过空间耦合等方式在本区段产生干扰[10]，该干扰可能导致轨道电路信号的误动作，需要分析相邻线路互阻抗以设计正确的轨道电路。对于低频轨道电路，可忽略大地对轨道互阻抗影响，但对于高速铁路轨道电路（f =1 700～2 600Hz），应考虑大地对轨道互阻抗影响。

对于轨道互阻抗计算有多种方法。根据电磁场理论推导满足边界条件的波动方程，分析轨道电路的传输特性，该方法分析严谨但计算量大；采用数值计算方法可考虑不同的介质分布，但该方法对操作人员有一定的技术要求；根据Carson地阻抗公式计算轨道互阻抗，考虑了大地对轨道互阻抗影响，但涉及复数计算，计算复杂。

针对以上问题，本文采用Carson地阻抗简化公式（Deri地阻抗公式）计算轨道互阻抗，考虑轨道电路空间位置特点，并采用泰勒公式对所求解进行化简，得到快速计算轨道互阻抗的简化公式。本文简化的轨道互阻抗公式只涉及轨道间距、轨道高度、信号频率和土壤电导率基本参数，便于计算且准确度高，适用于工程计算；同时，本文简化公式给出了轨道互阻抗中电阻和电抗的显式表达式。

1 快速计算轨道互阻抗简化公式推导

1.1 轨道互阻抗求解问题

对于多条轨道并行运行情况，相邻轨道通过空间耦合存在邻线干扰问题。图1为两条并行轨道简化图，由图可见，轨道1与轨道2之间存在耦合互感M，当轨道1存在轨道电路信号时，即图1中电流I，该信号将在轨道1周围产生磁场，并通过空间耦合方式在轨道2上产生干扰。若在考虑大地影响情况下求解轨道互阻抗，可采用Carson地阻抗公式[11]。

图1 两条并行轨道简化Fig.1 Simplified diagram of two parallel tracks

图2为地面上双导线系统，在考虑大地影响情况下，导线k与导线l单位长度的互阻抗可由Carson地阻抗广义积分形式表示为

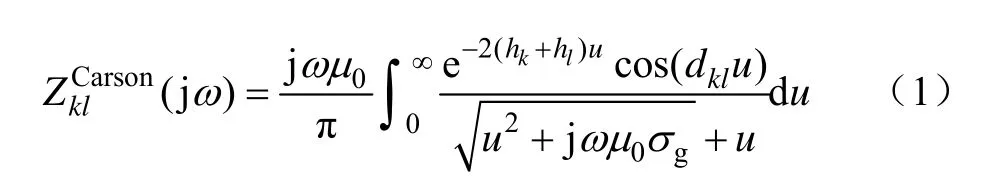
图2 地面上双导线系统Fig.2 Double wire system above the ground

式中，ω为信号角频率；μ0为真空磁导率；σg为大地电导率；hk为导线k到地面距离；hl为导线l到地面距离；dkl为两导线水平距离。

为克服式（1）求解收敛的困难，Gary在研究电力系统故障时提出复深度地回路，并由A. Deri等人[12]在理论上证明了Carson方法与复深度地回路方法的关系，将大地用一组地回流导线代替[13]，简化了Carson对地面上导线自阻抗和互阻抗的求解，即Deri地阻抗公式。图3为低频近似条件下，导线的镜像及镜像地回流线。图中，l'为镜像导线，l''为镜像地回流导线，p为大地中低频近似趋肤深度。

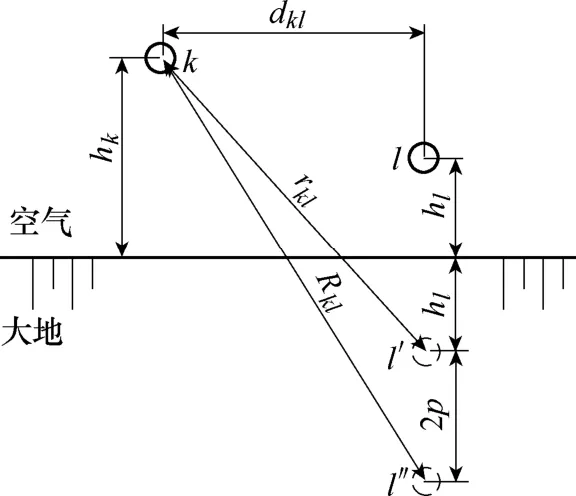
图3 导线的镜像及地回流线Fig.3 Tire image and ground return wire

根据Deri简化公式，式（1）可近似表示为

式中，rkl为导线k与导线l的镜像导线之间距离；Rkl为导线k与导线l的镜像地回流导线之间距离。有

1.2 采用Deri地阻抗公式求解轨道互阻抗

图4为两条并行轨道互阻抗。图中，d为一个轨道中两钢轨的间距（一般取值为1.435m）；D为相邻轨道的间距；h为钢轨中心线到地面的距离。

将钢轨等效为其中心线处的导线，根据式（2）计算钢轨1与钢轨3互阻抗为

同理，计算钢轨1、2与钢轨3、4互阻抗为

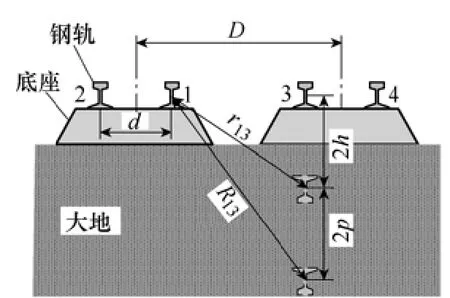
图4 两条并行轨道互阻抗Fig.4 Mutual impedance of two parallel tracks

式中，rij为钢轨i与钢轨j的镜像间距；Rij为钢轨i与钢轨j的镜像地回流线间距。

所以，当钢轨1、2组成的轨道电路通入信号时，采用Deri公式计算轨道互阻抗为1.3 轨道互阻抗公式化简

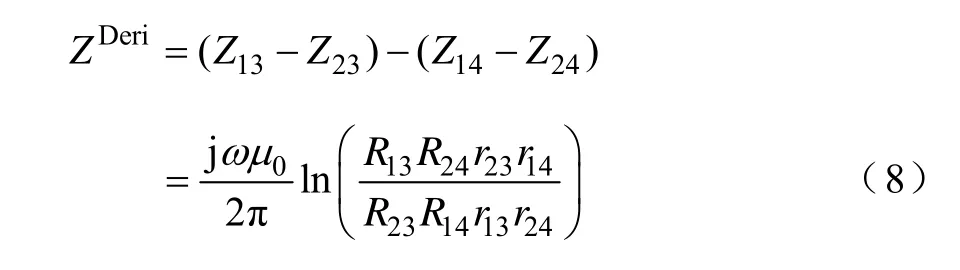
式（8）涉及参数多，计算复杂，不适用于工程计算。根据高速铁路轨道的空间位置特点，有

根据式（9）和式（10），通过泰勒公式和余弦定理对式（8）进行整理化简可得

式中

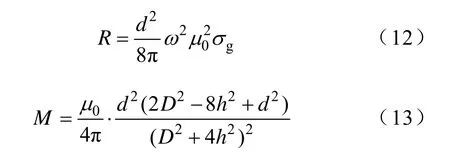
对式（8）的具体简化方法和过程见附录。由式（11）～式（13）可看出，该化简公式给出了轨道互阻抗中电阻和电抗的显式表达式；并且通过轨道间距、轨道高度、信号频率及土壤电导率四个基本参数可快速求解轨道互阻抗。

2 数值算例分析

2.1 大地对轨道互感影响

不考虑大地影响时，将钢轨等效为其中心线处的导线，单位长度轨道互感可表示为[14]

通过式（8）计算考虑大地影响时轨道互感M有大地，图5为有、无大地时轨道互感的相对差异。选取计算参数为D=5～15m，h=0.2m、0.4m、0.7m，f = 1 700Hz，σg=0.01S/m。相对差异计算式为

图5 有、无大地时轨道互感的相对差异Fig.5 Relative difference between track mutual inductance with and without earth return

由图5可知，在不同轨道高度和轨道间距时，考虑大地影响和不考虑大地影响两种情况下，轨道互感的相对差异在5%～30%之间，因此对于高速轨道电路，应该考虑大地对轨道互感的影响。

2.2 轨道间距与轨道高度变化的影响

当D=5m，h=0.4m，f =1 700Hz，σg=0.01S/m时，由式（8）计算轨道互阻抗，其中电阻部分为0.147mΩ，电抗部分为0.169Ω（轨道长度为1 000m）。由此可见在轨道互阻抗中，电阻远小于电抗，因此主要验证化简式（11）中电抗部分的正确性，同样在计算过程中取轨道长度为1 000m。

根据实际情况，相邻轨道间距最少为5m，轨道高度为0.4m左右，考虑四线并行，选取计算参数为：D=5～15m，h=0.2m、0.4m、0.7m，f =1 700Hz，σg= 0.01S/m。分别根据式（8）和式（11）计算轨道互阻抗中电抗部分，其对比结果如图6所示，图中XDeri为式（8）计算结果，X为式（11）计算结果。图7为两式计算轨道互阻抗中电抗的相对差异，该相对差异用δ1表示，并以XDeri为基准，其相对差异计算式与式（15）类似。

由图6可知，在轨道间距和轨道高度变化时，式（11）与式（8）求解结果基本吻合，验证了化简式的正确性。由图7可知，不同情况下，两式求解结果最大相对差异在2.5%以下。考虑到轨道高度一般在0.4m左右，根据图7可认为两式求解结果相对差异在1%以下。

图6 不同轨道间距和轨道高度时X与XDeri对比Fig.6 Comparison between X and XDeriwith different track spaces and track heights

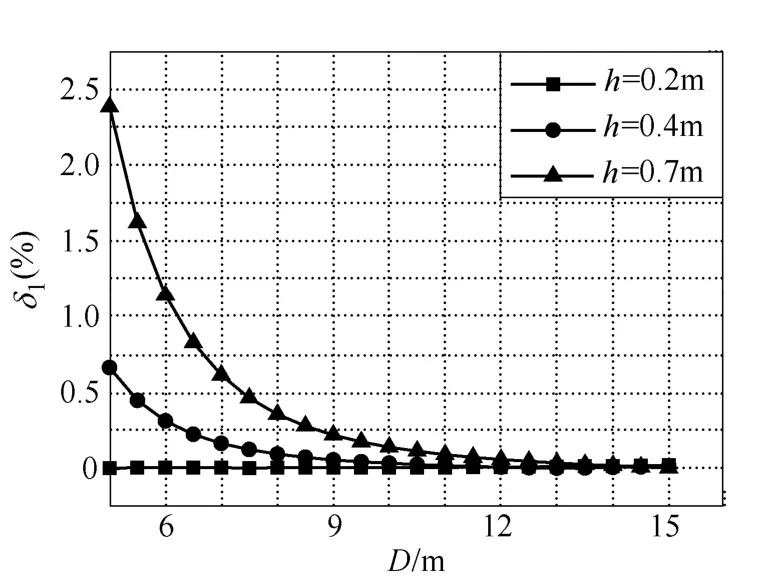
图7 不同轨道间距和轨道高度时X与XDeri相对差异Fig.7 Relative difference between X and XDeriwith different track spaces and track heights

2.3 信号频率和土壤电导率变化的影响

根据实际轨道电路运行情况，选取计算参数为D = 5m，h=0.4m，f =1 700Hz、2 000Hz、2 300Hz、2 600Hz，σg=0.01～1S/m。分别根据式（8）和式（11）计算轨道互感，其对比结果如图8所示，图中MDeri为式（8）计算结果，M为式（11）计算结果。两式计算轨道互感的相对差异如图9所示，该相对差异用δ2表示，并以MDeri为基准，其相对差异计算式与式（15）类似。

由图8可知，信号频率和土壤电导率变化时，式（11）与式（8）求解结果相差小。由图9可知，信号频率和土壤电导率变化时，式（8）与式（11）所求结果的相对差异在4%以下。考虑到大地电导率一般小于0.5S/m，根据图9可认为两式所求结果相对差异在1%以下。

通过以上计算可知，在计算轨道互阻抗时，应考虑大地对其的影响；在不同轨道间距、轨道高度、信号频率及土壤电导率情况下，本文化简公式求解轨道互阻抗的结果与Deri地阻抗公式求解结果相对差异小，适用于工程计算。

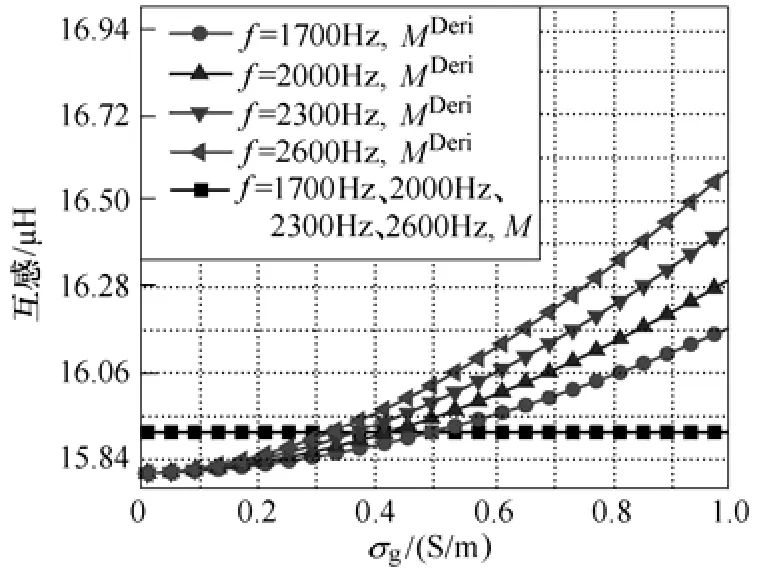
图8 不同信号频率和土壤电导率时M与MDeri对比Fig.8 Comparison between M and MDeriwith different signal frequencies and soil conductivities

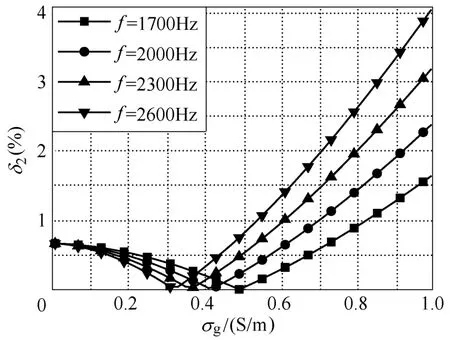
图9 不同信号频率和土壤电导率时M与MDeri相对差异Fig.9 Relative difference between M and MDeriwith different signal frequencies and soil conductivities

3 结论

本文根据Deri地阻抗公式及轨道电路空间位置特点，推导了考虑大地影响情况下高速轨道互阻抗简化公式。计算表明：计算高速轨道互阻抗时，应考虑大地影响；本文推导的计算轨道互阻抗简化公式计算简便、准确度高，适用于工程计算；本文简化公式给出了轨道互阻抗中电阻和电抗的显式表达式；轨道互阻抗中电阻部分远小于电抗部分，可忽略不计。

附 录

根据泰勒公式得

对式（A1），若

则将式（8）表示为式中

根据图4，将式（A5）整理为

因为轨道电路信号频率可使式（9）成立，所以对于式（A7）中，有

根据式（A3），将式（A7）化简整理为

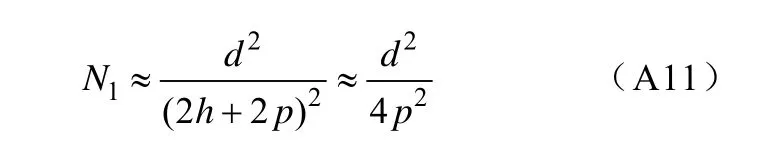
对于式（A6），其中参数主要为钢轨1、2与钢轨3、4镜像钢轨之间的距离，如附图1所示，四边形123' 4'为平行四边形，r13和r24为平行四边形的对角线，r23和r14为平行四边形的对边，所以有在123'△中，利用余弦定理可得

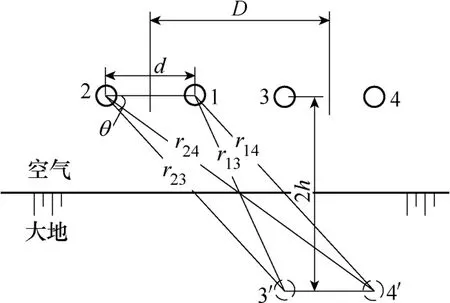
附图1 钢轨1、2与钢轨3、4的镜像钢轨之间的距离App. Fig.1 Distance between rail 1, 2 and the rail image of rail 3, 4

在△124'中，利用余弦定理可得

根据式（A12）～式（A14），将式（A6）整理得

轨道空间位置特点可使式（10）成立，并根据式（A1）对式（A15）进行泰勒公式展开，取前两项并化简整理得

根据式（A11）和式（A16），将式（A4）化简整理可得式（11）。

参考文献

[1] 卢祖文. 高速铁路轨道技术综述[J]. 铁道工程学报, 2007, 100(1): 41-54.

Lu Zuwen. Overall comments on track technology high-speed railway[J]. Journal of Railway Engineering Society, 2007, 100(1): 41-54.

[2] 朱高明. 国内外无砟轨道的研究与应用综述[J]. 铁道工程学报, 2008, 118(7): 28-30.

Zhu Gaoming. Overall comments on study and application of ballastless track at home and abroad[J]. Journal of Railway Engineering Society, 2008, 118(7): 28-30.

[3] 刘建强, 郑琼林, 杨其林. 高速列车牵引传动系统与牵引网谐振机理[J]. 电工技术学报, 2013, 28(4): 221-227.

Liu Jianqiang, Zheng Qionglin, Yang Qilin. Resonance mechanism between traction drive system of high-speed train and traction network[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 221-227.

[4] 方璐, 罗安, 徐先勇, 等. 高速电气化铁路新型电能质量补偿系统[J]. 电工技术学报, 2010, 25(12): 167-176.

Fang Lu, Luo An, Xu Xianyong, et al. A novel power quality compensator for high-speed electric railway[J]. Transactions of China Electrotechnical Society, 2010, 25(12): 167-176.

[5] 陈民武. 基于GO法的高速铁路牵引变电所可靠性评估[J]. 电力系统保护与控制, 2011, 39(18): 56-61.

Chen Minwu. The reliability assessment of traction substation of high speed railway by the GO methodology[J]. Power System Protection and Control, 2011, 39(18): 56-61.

[6] 刘育权, 吴国沛, 华煌圣, 等. 高速铁路牵引负荷对电力系统的影响研究[J]. 电力系统保护与控制, 2011, 39(18): 150-154.

Liu Yuquan, Wu Guopei, Hua Huangsheng, et al. Research on the effects of high-speed railway traction load on the power system[J]. Power System Protection and Control, 2011, 39(18): 150-154.

[7] Luca D R, Zhang Zichi, Sergio A P. Boundary–element computation of per-unit-length series parameters of railway lines[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 825-832.

[8] Andrea M, Paolo P. Determination of the electrical parameters of railway traction lines: calculation, measurement, and reference data[J]. IEEE Transactions on Power Delivery, 2004, 19(4): 1538-1546.

[9] 李智宇, 郑昇, 徐宗奇, 等. 高速条件下ZPW—2000A无绝缘轨道电路耦合干扰分析及对策[J]. 中国铁道科学, 2010, 31(3): 99-106.

Li Zhiyu, Zheng Sheng, Xu Zongqi, et al. Analysis on the coupling disturbance of ZPW-2000A jointless track circuit under high speed condition and countermeasures[J]. China Railway Science, 2010, 31(3): 99-106.

[10] 张建平. ZPW—2000型轨道电路的邻线干扰[J]. 铁路技术创新, 2009(1): 53-56.

[11] Carson J R. Wave propagation in overhead wires with ground return[J]. Bell Systems Technical Journal, 1926,5: 539-556.

[12] Deri A, Tevan G, Semlyen A, et al. The complex ground return plane a simplified model for homogenous and multilayer earth return[J]. IEEE Transactions on Power Apparatus & Systems, 1981, 100(8): 3686-3693.

[13] 法哈德·拉奇迪, 谢尔盖·特卡琴科. 电磁场与传输线的相互作用[M]. 谢彦召, 译. 北京: 清华大学出版社, 2013.

[14] 马信山, 张济世, 王平. 电磁场基础[M]. 北京: 清华大学出版社, 2008.

杜学龙 男，1988年生，博士研究生，研究方向为高速铁路轨道电路邻线干扰。

E-mail: xuelong.99@163.com（通信作者）

邹 军 男，1971年生，教授，博士生导师，研究方向为电磁场计算及应用。

E-mail: zoujun@tsinghua.edu.cn

作者简介

收稿日期2014-08-25 改稿日期 2015-04-08

中图分类号：TM153