基于局部图嵌入加权罚SVM的模拟电路故障诊断方法

廖 剑史贤俊周绍磊肖支才（1. 中国人民解放军第91550部队 大连 116000 . 海军航空工程学院控制工程系 烟台 64001）



基于局部图嵌入加权罚SVM的模拟电路故障诊断方法

廖 剑1,2史贤俊2周绍磊2肖支才2
（1. 中国人民解放军第91550部队 大连 116000 2. 海军航空工程学院控制工程系 烟台 264001）

摘要针对传统支持向量机（SVM）在模拟电路故障诊断应用中存在的不足，提出一种基于局部图嵌入加权罚支持向量机（LGEWP-SVM）的模拟电路故障诊断新方法。通过在保持数据整体类间间隔最大化的基础上优化数据流形的局部分布，同时在惩罚系数中引入数据的全局分布信息，设计了一种依赖于数据分布的新型支持向量机。该方法有效融合了数据的先验分布信息，增强了算法的抗干扰能力，提高了模型的诊断准确度。实验结果验证了所提方法的有效性。

关键词：模拟电路 故障诊断 支持向量机 数据流形

国家自然科学基金重点资助项目（61203168）。

Analog Circuit Fault Diagnosis Based on Local Graph Embedding Weighted-Penalty SVM

Liao Jian1,2Shi Xianjun2Zhou Shaolei2Xiao Zhicai2
（1. The Troop 91550 of PLA Dalian 116000 China 2. Department of Control Engineering Naval Aeronautical and Astronautical University Yantai 264001 China）

Abstract This paper proposes a method for analog IC diagnosis based on local graph embedding weighted-penalty support vector machine (SVM), to overcome the shortcomings of fault diagnosis method based on traditional SVM. A new type of SVM lying on data distribution is designed. Herein, maximize the inter-class margin of the entire data while optimizing local distribution of the data manifold, meanwhile, introduce the global data distribution information in error costs. The proposed method effectively combines the prior distribution information to improve the robustness and increase the diagnosis accuracy. The simulation results show the effectiveness of the algorithm.

Keywords：Analog circuit, fault diagnosis, support vector machine, data manifold

0 引言

片上系统技术的发展使得模拟电路的测试与诊断变得越发重要[1]。但模拟电路自身存在故障模型欠佳、元件容差、故障参数连续和电路非线性等特点[2]，使得模拟电路故障诊断技术发展缓慢，至今仍无实用方法。20世纪90年代以来，随着人工智能技术（主要是机器学习方法）研究的复兴，越来越多学者将其应用到模拟电路故障诊断中，并取得了显著成果[1-10]。基于机器学习的故障诊断方法，如神经网络（Neural Networks, NN）[2-5]和支持向量机（Support Vector Machine, SVM）[6-10]，由于不需要准确的数学模型，因而非常适合于有容差的模拟电路故障诊断。M. Aminian等基于NN进行模拟电路故障诊断取得了大量的研究成果，并获得了比故障字典法更好的诊断效果[2-5]。但是NN基于经验风险最小化，在训练的过程中普遍存在收敛速度慢、容易陷入“局部最优”且当故障样本有限时其泛化能力难于得到保证等缺点。文献[6-10]对模拟电路诊断技术研究的不断深入和发展，提出了基于SVM的模拟电路故障诊断技术并取得了优于NN的识别效果。SVM作为一种基于统计学习理论的机器学习方法，克服了NN方法的固有缺点，在解决小样本、非线性及高维模式识别等问题中表现出结构简单、全局最优和泛化能力强等特点，被看作是对传统分类器的一个好的替代，已在模拟电路故障诊断中得到成功应用[6-10]。但SVM在构造最优分类超平面时，仅仅关注数据整体类间的可分离性，忽视了类内数据的结构信息[11]，导致在数据中存在非线性流形结构时，其分类边界过于光滑，严重影响了SVM的分类性能。在实际问题中，大部分样本都是高度相关的，也就是说，这些样本至少局部分布在一个低维流形上[12]。特别地，一般电路的输出和电路的故障机理之间往往存在非线性关系[13,14]，因此，传统SVM仅仅关注类间间隔信息对模拟电路故障诊断分类问题来说是远远不够的。同时，传统SVM在构造分类超平面时所有的样本都具有相同的作用，而故障诊断中采集的测试样本往往含有噪声和野点，这些“异常”样本在特征空间中常常位于分类平面附近，容易导致获得的分类超平面在反映数据的分布时发生偏差，从而影响诊断效果[15]。针对上述情况，本文提出一种融合数据全局和局部先验信息的局部图嵌入加权罚支持向量机（Local Graph Embedding Weighted-Penalty SVM, LGEWP- SVM）的故障诊断方法，该方法在构造目标函数时，除了要求保持数据整体类间间隔最大化的同时还加入对数据流形局部分布的优化，试图利用数据的流形局部信息去指导样本类间间隔最大值的取得。同时还在目标函数中融入样本的全局结构信息，根据样本全局分布权重对不同的样本采用不同的惩罚权系数，对含有噪声的样本赋予较小的权重，从而达到消除噪声的影响，提高算法的抗干扰能力。

1 SVM及其应用于故障诊断的不足

1995年，V. N. Vapnik[16]基于结构风险最小化原则提出SVM分类算法，由于其能有效解决小样本、非线性及高维模式识别等问题且通常具有良好的学习和推广能力而得到广泛研究并已成功应用于模式识别和故障诊断等领域。的目标函数就是学习一个分类器使得两类之间的间隔最大化

对于线性不可分问题，对每个样本引入一个松弛变量ξi，支付一个代价ξi将间隔软化。目标函数由原来的变成

相应的约束条件变为式中，C称为惩罚系数，C＞0，一般由应用问题决定，用以在最大化间隔和最小化错分程度之间寻求一个满意的平衡。

从定理1可知，传统SVM在约束条件中自然地暗含了对类间可分离性的一个下界，这与模式识别的大间隔准则要求是一致的。但是，SVM却忽视了类内先验的结构信息，这些信息对于分类问题至关重要。文献[17]指出，对于复杂的模式识别问题，如果仅仅关注数据的类间间隔而忽略数据的先验分布信息，将使训练得到的分类器边界过于光滑，从而对于复杂问题的分类准确度将明显下降。同时，对于大部分模拟故障诊断问题，由于电路的输出和电路的故障机理之间往往存在非线性关系，且采用小波、FFT变换方法提取的故障特征样本常局部嵌入在一个低维流形上[14]。因此，如果只关注故障样本的类间间隔，将不能得到很好的分类诊断效果。

同时，由式（3）可见，在SVM中，惩罚系数C对所有样本的惩罚都是相同的，这样往往会造成“异常”样本对分类边界影响过大，导致获得的分类超平面在反映数据的分布时产生偏差，所以一个很自然的想法就是根据样本的重要程度应用不同的惩罚权系数。

2 LGEWP-SVM及其故障诊断

为了更好地在SVM中融入数据的先验结构信息，本文提出一种局部图嵌入加权罚支持向量机，试图在构造最优分类超平面的同时考虑数据的整体类间间隔和数据流形的局部信息，使分类超平面对数据分布敏感。为了更好地描述LGEWP-SVM，先给出如下定义：

根据光谱图理论[19]，具有权重矩阵W的加权邻接图G能有效刻画样本流形的局部几何结构，但仅有一个整体图并不足以反映样本间的判别结构，为此，可以针对类内样本和类间样本分别构建加权邻接类内图和类间图，分别用于刻画数据流形

的局部结构信息和局部判别信息。

定义2 （局部离散度矩阵）[17]：设Lw和Lb分别为图Gw和Gb的拉普拉斯矩阵，则矩阵Hw称为局部类内图离散度矩阵，Hw=XLwXT=X（ Tw-Ww）XT；矩阵Hb称为局部类间图离散度矩阵，Hb=XLbXT= X（ Tb-Wb）XT。其中，T（·）为l×l对角矩阵，其对角线上元素定义为为图Γ（·）的权重矩阵。Hw和Hb统称为局部离散度矩阵。

上述定义中，局部类内图离散度矩阵wH体现了输入样本流形的局部结构信息，局部类间图离散度矩阵bH体现了输入样本流形的局部判别信息。

定义3 （样本xi全局权重）：设Wij为图G的加权邻接矩阵，定义iρ为样本xi的全局权重，可表示为

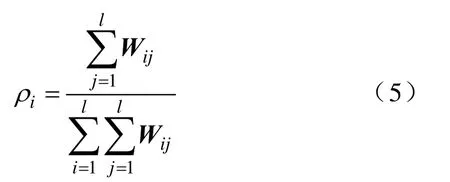
全局权重提供了流形全局的一个自然度量，如果样本点xi的全局权重iρ越大，则xi的近邻在全局流形结构上分布越紧凑，意味着xi与其近邻之间越相似。反之，则说明xi与其近邻越不相似，越有可能是野值点，对其错分应赋予较小的惩罚权重。

根据模式识别的大间隔准则，在输出空间中，期望在图wG中的近邻样本尽可能地紧凑，同时在图b G中的近邻样本尽可能地分散。且根据样本对分类边界的影响大小采用不同的惩罚权系数，在目标函数中，对含有噪声的样本赋予较小的权值，从而达到消除噪声的影响。因此，LGEWP-SVM方法的原始优化问题可描述为

式中，C是一个惩罚系数，C＞0；λ 是正则化参数，0 λ≥，用于调节局部流形信息的相对重要性；ξi为松弛向量，ξi=（ξ1,…,ξl）。

类似于传统SVM的推导方法，将原始问题转化为求其对偶问题的最优解，可得原始优化问题式（6）和式（7）的对偶问题为

式中，iα为Lagrangian乘子；I为单位矩阵。且LGEWP-SVM原始优化问题中投影向量*w和偏置变量*b分别为

同传统SVM相比，对于线性不可分问题，同样可以把样本映射到高维特征空间中，然后在特征空间中构造最优分类超平面。

与基于传统SVM的故障诊断方法一样，基于LGEWP-SVM的模拟电路故障诊断方法，也分为训练和诊断两个阶段。首先，先对诊断电路施加激励，采用合适的故障特征提取方法提取电路在不同故障状态下的特征组成训练集，然后使用LGEWP- SVM方法训练诊断分类器对故障进行分类。

3 故障诊断实例

在现有的模拟电路故障诊断文献中，电路元件的故障模型设计一般采用两种方法：

（1）故障元件的取值设定在一个较大的区间。设电路中的元件标称值为n；t为元件的容差，则元件的正常值的波动范围为［n(1-t),n(1+t )］。当电路中元件发生故障时，也常设其故障值容差为f，所以当元件发生偏小故障时，该元件的值位于区间［(1-f) n,(1-t) n］。同理，当元件发生偏大故障时，元件的值位于区间［(1+t) n,(1+f) n］。这种故障模型可以对器件的早期故障进行检测或预测。如文献[9,13-15, 20-23]就是采用这种故障模型。

（2）故障元件的取值是一个很小的容差波动区间。也即设定元件的故障值为一单点值加上相应的元件容差。这是目前模拟电路故障诊断中比较流行的一种模型，可用于诊断电路中已出现的故障。如文献[1-5,7,8,10,24]就采用这种故障模型。

本文将分别在两个电路上使用这两种故障模型进行仿真实验，第一个CUT使用第一种故障模型，第二个CUT使用第二种故障模型，验证该方法的有效性。

3.1 第一个CUT验证

3.1.1 电路模型、参数及故障仿真设置

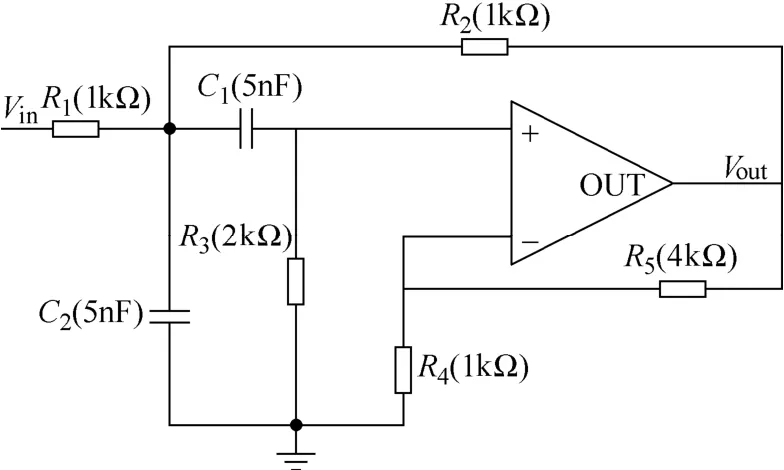
图1 Sallen-Key带通滤波器电路Fig.1 Sallen-Key circuit

第一个实验电路为Sallen-Key带通滤波器[8-10,14,21,22]，是众多文献进行相关方法验证的标准电路之一。该电路结构及元件标称值如图1所示，输入节点为Vin，输出节点为Vout。仿真实验中，设定电路中电容元件正常容差为10%，电阻元件正常容差为5%，并假设电路中无源器件发生单故障，按照第一种故障模型设计，假定元件发生故障时，故障容差为50%。即元件发生偏小故障时其值位于区间［50%n,(1-t) n］，发生偏大故障时其值位于区间［(1+t) n,150%n］。发生故障元件为R2、R3、C1和C2。故障模式设置与文献[9]完全一致，八种软故障见表1，符号⇑和⇓分别表示偏大和偏小故障。

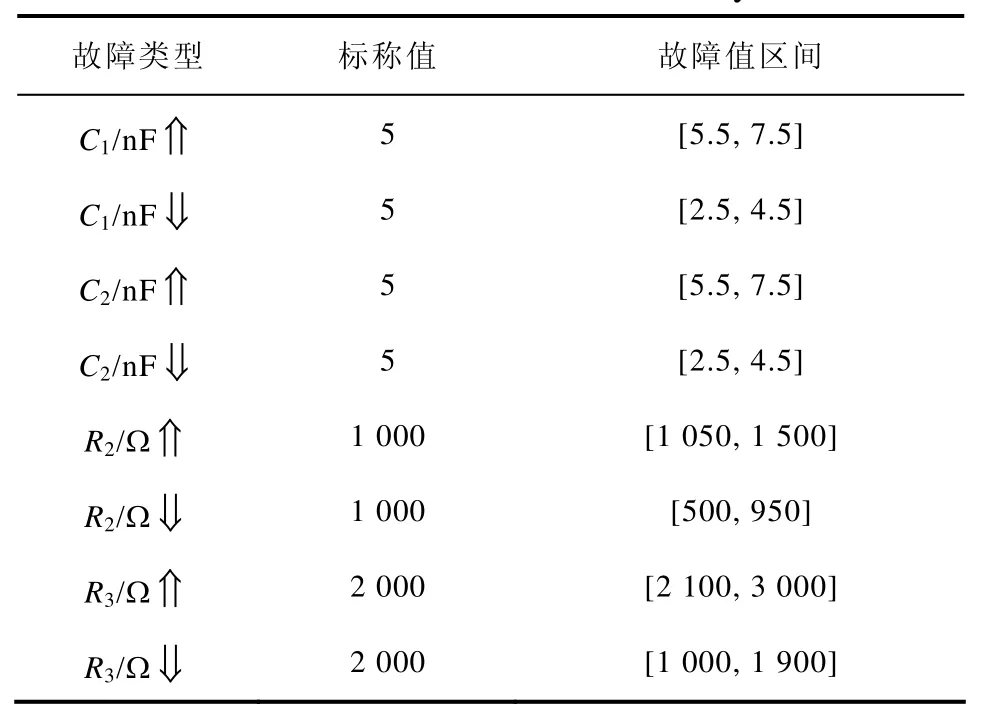
表1 Sallen-Key电路中软故障模式Tab.1 Soft fault modes in Sallen-Key circuit

3.1.2 特征提取

按照表1，对电路的正常状态和故障状态分别进行仿真，实验中电路某一时刻只发生单故障，且其他元件在其容差范围内随机变化。正常状态下所有元件在其容差范围内变化。给Sallen-Key带通滤波器施加幅度为1V的正弦交流电，对电路进行十倍频AC Sweep分析，每十倍频10个频点，通过仿真分析可知，电路的中心频率为30kHz，因此，实验中设置扫频起始频率为1kHz，终止频率为1MHz，仿真采样Vout节点电压。每种状态均进行100次Monte-Carlo分析，共采样900组数据。图2给出了八种故障状态的部分频谱特性曲线（每种状态5个样本）。对于采样的数据，本文采用文献[8]的方法提取故障特征。因为Sallen-Key是一个带通滤波器，所以分别选择其谐振频率、下边带频率、上边带频率、峰值输出电压和上边带或下边带频率对应的电压作为故障诊断的特征向量。详细的故障特征提取步骤和故障特征样本集处理方法参见文献[8]。

3.1.3 故障诊断结果分析

将每种故障状态下的100组特征数据分为两部分，其中50组用于训练故障分类器，剩下的50组用于诊断仿真结果，总的训练样本数为50×9=450组。然后根据式（8）～式（12），使用网格搜索法搜索最佳的LGEWP-SVM参数组合，采用一对一策略，训练36个两类分类器对电路进行诊断，重复10次，记录10次实验的平均结果见表2，表中NF表示无故障状态。表2分别列出了LGEWP-SVM方法采用线性核和非线性核情况下的故障诊断结果，非线性核采用RBF核函数形式。为进行对比，表中也同时列出了基于SVM[9]方法在采用两种核函数情况下的故障诊断结果。

图2 Sallen-Key电路在八种故障状态下的部分频谱特性曲线Fig.2 Part of the spectrum curve in eight types of faults of Sallen-Key circuit

表2 Sallen-Key电路故障诊断结果Tab.2 The diagnosis results of Sallen-Key circuit

由表2可以看出：①无论是SVM方法还是LGEWP-SVM方法，在采用非线性核函数的情况下（或者说核技巧），都能增强算法的故障分类性能，在采用RBF核的情况下，SVM和LGEWP- SVM方法的平均故障诊断率分别为0.963和0.973，明显高于采用线性核的0.935和0.957；②融合了数据先验分布信息的LGEWP-SVM方法，其故障诊断率要高于仅仅关注类间间隔的SVM方法；③在某些故障状态下，甚至采用线性核形式的LGEWP-SVM方法取得的故障诊断率都要高于采用非线性核形式的SVM方法取得的故障诊断率。可见，本文方法确实能提高模拟电路的故障诊断准确度。

3.2 第二个CUT验证

3.2.1 电路模型、参数及故障仿真设置

本文再以两级四运放低通滤波器电路[24]为例考察LGEWP-SVM方法的非线性处理能力和抗干扰能力。两级四运放低通滤波器的电路结构及元件标称值如图3所示。

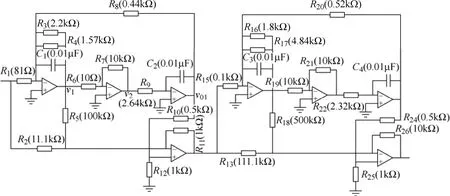
图3 两级四运放低通滤波器电路Fig.3 Two-stage four-op-amp biquad low-pass filter circuit

与实验1相同，仿真中设定电路中电容正常容差为10%，电阻正常容差为5%。不同之处在于，本次实验假定电路元件发生单点故障，即上述故障模型设计中的第二种方法。参考文献[24]，假设电路中的典型故障元件为C1～C4、R3、R4、R6～R9、R16、 R19、R21和R21，15种软故障的详细情况见表3。

表3 两级四运放低通滤波器电路中软故障模式Tab.3 Soft fault modes in two-stage four-op-amp biquad low-pass filter circuit

3.2.2 特征提取

按照表3，对电路正常和故障状态分别进行仿真，实验中每次设置一个故障，其他元件在其容差范围内变化。给电路施加5V、宽度为100μs的窄脉冲，对电路进行瞬态分析，设置Pspice仿真时间为200μs，采样率为500k/s，程序运行2μs后开始采样数据，共进行100次Monte-Carlo分析，这样共采样1 600组数据，每组100个数据点。然后采用文献[24]的特征计算方法，对所有采样数据进行分数阶傅里叶变换（Fractional Fourier Transform, FrFT），寻找最优p值下的FrFT值作为相应的故障特征组成故障诊断用数据集。同样，详细的故障特征提取步骤和故障特征样本集处理参见文献[24]。

3.2.3 故障诊断结果分析

将每种故障状态下的100组FrFT特征数据随机分为两部分，其中50组用于训练故障分类器，剩下的50组用作诊断仿真结果，共进行两组实验。一组直接用于训练故障分类器，另一组则对每一个特征样本添加相应的白噪声后用于训练故障分类器。LGEWP-SVM核函数形式使用RBF核函数，并使用网格搜索法搜索最佳的LGEWP-SVM参数组合，采用一对一分类策略对电路进行诊断，每次实验重复10次，记录相应10次实验的平均结果见表4和表5，其中表4为不含噪声特征数据的故障诊断结果，表5为添加了白噪声后的特征数据的故障诊断结果。同时表中也相应列出了基于SVM和LS-SVM[8]方法的故障诊断结果。

表4 特征数据不含白噪声情况下的电路故障诊断率Tab.4 Diagnosis accuracies of the circuit without white noise in feature data

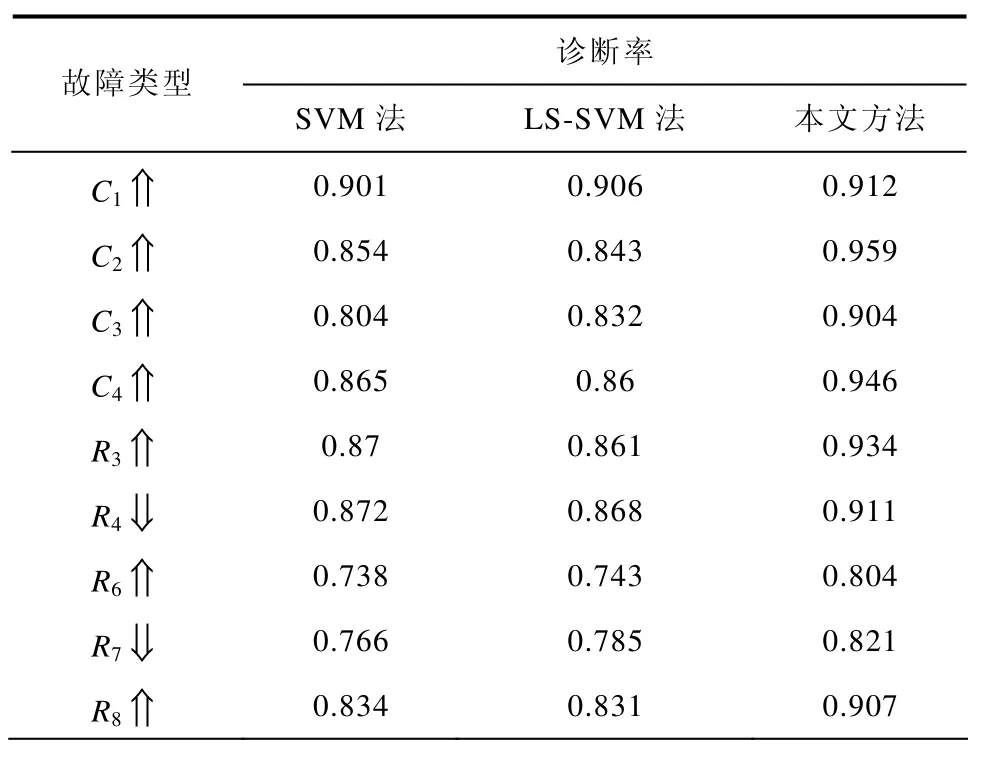
表5 特征数据包含白噪声情况下的电路故障诊断率Tab.5 Diagnosis accuracies of the circuit with white noise in feature data

（续）

从表4和表5可以得出如下结论：

（1）对含噪声数据，三种故障诊断方法的故障诊断率都有所降低，说明实际故障诊断中的噪声数据将进一步增加模拟电路故障诊断的难度。

（2）对于具有高度非线性的数据，无论是含噪声数据还是不含噪声数据，融合了数据先验分布信息的LGEWP-SVM方法的故障诊断率都要明显高于SVM和LS-SVM方法，如对于电路中最难诊断的R6⇑、R7⇓和R9⇑故障，LGEWP-SVM方法的故障诊断率都要明显高于SVM和LS-SVM方法。

（3）相对于SVM和LS-SVM方法，加入了全局分布信息的加权罚LGEWP-SVM方法的鲁棒性更好，对噪声和野点数据的抗干扰能力更强。

比较表4和表5，LGEWP- SVM方法对于不含噪声数据的平均故障诊断率为0.924，含噪声数据的平均故障诊断率为0.908，仅仅下降了1.6%。而对于SVM和LS-SVM方法，不含噪声数据的平均故障诊断率为0.896和0.901，含噪声数据的平均故障诊断率分别为0.841和0.84，则分别下降了5.5%和6.1%。可见，本文方法在实际的带噪声数据的故障诊断中将更有优势，有可能取得更高的故障诊断准确度。

4 结论

本文针对传统SVM在模拟电路故障诊断应用中存在的不足，提出一种基于局部图嵌入加权罚支持向量机的模拟电路故障诊断新方法。该方法在构造目标分类函数时，除了要求保持数据整体类间间隔最大化的同时还加入对数据流形局部分布的优化，试图利用数据的流形局部信息去指导样本类间间隔最大值的取得。同时还在目标函数中融入样本的全局结构信息，根据样本全局分布权重对不同的样本采用不同的惩罚权系数，对含有噪声的样本赋予较小的权重，能提高算法的抗干扰能力。采用线性Sallen-Key带通滤波器电路和具有弱非线性的两级四运放低通滤波器电路验证了方法的有效性，并与基于SVM和LS-SVM的故障诊断方法进行了对比。结果表明，所提方法能有效提高模拟电路的故障诊断率，并具有较强的鲁棒性，具有较大的应用优势。需要指出的是，尽管本文方法在分类性能上取得了一定的提高，但随之造成的参数选择问题却是一个值得考虑的问题，同时如何提高其计算效率也是一个有待进一步研究的问题。

参考文献

[1] Peng M, Chi K T, Shen M, et al. Fault diagnosis of analog circuit using systematic tests based on data fusion[J]. Circuit Systems and Signal Processing, 2013, 32(2): 525-539.

[2] Aminian M, Aminian F. A modular fault-diagnostic system for analog electronic circuits using neural networks with wavelet transform as a preprocessor[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(5): 1546-1554.

[3] Aminian M, Aminian F. Neural-network based analog circuit fault diagnosis using wavelet transform as preprocessor[J]. IEEE Transactions on Circuit System II: Analog and Digital Signal Processing, 2000, 47(2): 151-156.

[4] Aminian M, Aminian F. Fault diagnosis of nonlinear circuits using neural networks with wavelet and fourier transforms as preprocessors[J]. Journal of Electronic Testing, 2001, 17(6): 471-481.

[5] Aminian M, Aminian F. Analog fault diagnosis of actual circuits using neural networks[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 544-550.

[6] Huang Jian, Hu Xiaoguang, Yang Fan. Support vector machine with genetic algorithm for machinery fault diagnosis of high voltage circuit breaker[J]. Measurement, 2011, 44(6): 1018-1027.

[7] Long Bing, Tian Shulin, Miao Qiang, et al. Research on features for diagnostics of filtered analog circuits based on LS-SVM[J]. IEEE Autotestcon, Systems Readiness Technology Conference, 2011, 124(1): 360-366.

[8] Long Bing, Tian Shulin, Wang Houjun. Diagnostics of filtered analog circuits with tolerance based on LS-SVM using frequency features[J]. Journal of Electronic Testing, 2012, 28(3): 291-300.

[9] 孙永奎, 陈光礻禹, 李辉. 基于自适应小波分解和SVM的模拟电路故障诊断[J]. 仪器仪表学报, 2008, 29(10): 2105-2109. Sun Yongkui, Chen Guangju, Li Hui. Analog circuit fault diagnosis method using adaptive wavelet analysis and SVM[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2105-2109.

[10] 宋国明, 王厚军, 姜书艳, 等. 最小生成树SVM的模拟电路故障诊断方法[J]. 电子科技大学学报, 2012, 41(3): 412-417. Song Guoming, Wang Houjun, Jiang Shuyan, et al. Fault diagnosis approach for analog circuits using minimum spanning tree SVM[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(3): 412-417.

[11] Xue Hui, Chen Songcan, Yang Qiang. Structural support vector machine[J]. Lecture Notes in Computer Science, 2008, 5263(1): 501-511.

[12] Lafon S, Keller Y, Coifman R R. Data fusion and multicue data matching by diffusion maps[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(11): 1784-1797.

[13] 崔江, 王友仁. 一种新颖的基于混合故障字典方法的模拟故障诊断策略[J]. 电工技术学报, 2013, 28(4): 272-278. Cui Jiang, Wang Youren. A novel strategy of analog fault diagnosis based on hybrid fault dictionaries[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 272-278.

[14] 韩海涛, 马红光, 曹建福, 等. 基于非线性频谱特征及核主元分析的模拟电路故障诊断方法[J]. 电工技术学报, 2012, 27(8): 248-254. Han Haitao, Ma Hongguang, Cao Jianfu, et al. Fault diagnosis method of analog circuits based on characteristics of the nonlinear frequency spectrum and KPCA[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 248-254.

[15] 唐静远, 师奕兵. 采用模糊支持向量机的模拟电路故障诊断新方法[J]. 电子测量与仪器学报, 2009, 23(6):7-12. Tang Jingyuan, Shi Yibing. New method of analog circuit fault diagnosis using fuzzy support vector machine[J]. Journal of Electronic Measurement and Instrument, 2009, 23(6): 7-12.

[16] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995.

[17] 陶剑文, 王士同. 局部保留最大信息差v-支持向量机[J]. 自动化学报, 2012, 38(1): 97-108. Tao Jianwen, Wang Shitong. Locality-preserved maximum information variance ν-support vector machine[J]. Acta Automatica Sinica, 2012, 38(1): 97-108.

[18] Wang Fei. A general learning framework using local and global regularization[J]. Pattern Recognition, 2010, 43(9): 3120-3129.

[19] Yan Shuicheng, Xu Dong, Zhang Benyu, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(1): 40-51.

[20] Han Han, Wang Houjun, Tian Shulin, et al. A new analog circuit fault diagnosis method based on improved mahalanobis distance[J]. Journal of Electronic Testing, 2013, 29(1): 95-102.

[21] 钟建林, 何友, 任献彬. 基于波形相似度的容差模拟电路软故障诊断[J]. 电工技术学报, 2012, 27(8): 222-229. Zhong Jianlin, He You, Ren Xianbin. Soft fault diagnosis based on waveform similarity for tolerance analog circuit[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 222-229.

[22] Li Xifeng, Xie Yongle. Analog circuits fault detection using cross-entropy approach[J]. Journal of Electronic Testing, 2013, 29(1): 115-120.

[23] Tadeusiewicz M, Halgas S. Multiple soft fault diagnosis of nonlinear circuits using the continuation method[J]. Journal of Electronic Testing, 2012, 28(4): 487-493.

[24] 罗慧, 王友仁, 崔江. 基于最优分数阶傅立叶变换的模拟电路故障特征提取新方法[J]. 仪器仪表学报, 2009, 30(5): 997-1001. Luo Hui, Wang Youren, Cui Jiang. New approach to extract analog circuit fault features based on optimal fractional Fourier transforms[J]. Chinese Journal of Scientific Instrument, 2009, 30(5): 997-1001.

廖 剑 男，1985年生，博士，主要研究方向为电路设计、测试与诊断。

E-mail: 251250544@qq.com（通信作者）

史贤俊 男，1968年生，博士，教授，主要研究方向为机器学习、模式识别和电路设计、测试与诊断。

E-mail: 18660501122@wo.com.cn

作者简介

收稿日期2013-11-18 改稿日期2014-01-07

中图分类号：TP181; TM930