基于材性的混凝土结构及构件冻融损伤模型试验研究
2016-04-07郑山锁付晓亮王子胜甘传磊
郑山锁, 汪 锋, 付晓亮, 王子胜, 甘传磊
(西安建筑科技大学 土木工程学院,西安 710055)
基于材性的混凝土结构及构件冻融损伤模型试验研究
郑山锁, 汪锋, 付晓亮, 王子胜, 甘传磊
(西安建筑科技大学 土木工程学院,西安710055)
摘要:基于蔡昊模型,通过理论推导并结合既有冻融材性试验数据,对模型中最大静水压力计算方法进行改进。进行9组材性试验,建立了混凝土水灰比和最大结冰速率之间的拟合关系,推导出最大静水压力的简化解析计算公式。采用ANSYS有限元软件,对构件截面温度场分布进行了模拟,得到考虑温度场修正的冻融损伤模型。最后,设计2组试件,对改进冻融损伤模型的准确性与可靠性进行试验验证,结果表明:修正后的采用动弹模损伤作为物理损伤指标的冻融损伤模型,可为RC构件与结构层面冻融损伤机理研究提供理论支撑。
关键词:混凝土结构;冻融;水灰比;温度场;结冰速率;相对动弹模量
从20世纪30年代起,严寒地区混凝土冻害问题备受国内外学者关注。目前,对于RC结构冻融损伤领域的研究,多集中于材料层面,而极少上升至构件层面[1-2],对于结构层面的研究则未见报道。对于RC结构冻融损伤程度,多依据现行耐久性规范进行评判。规范采用标准试件和统一化的冻融循环条件,无需考虑试件尺寸效应对于冻融损伤的影响。限于试验条件,RC构件和结构层面的冻融损伤评估方法需进一步探讨。既有构件层面的试验研究简单以冻融循环次数作为物理损伤指标,未能考虑试件尺寸效应的影响,且无法采用相同的冻融循环方法,导致其研究成果无法进行对比分析。综上,本文为对冻融损伤后RC结构的力学性能与抗震性能衰减规律进行研究,以混凝土动弹模量损失量D作为RC结构冻融损伤程度的物理损伤指标(已有研究[3-8]对此冻融损伤量化指标的科学性与合理性进行过佐证),从混凝土冻融损伤微观机理出发,基于现有的混凝土冻融损伤模型,结合本人的试验研究,建立可应用于RC结构构件层面的冻害损伤模型。
1蔡昊冻融损伤模型的修正
蔡昊[8]基于静水压力和损伤力学理论,以混凝土相对动弹模量作为损伤指标,提出了以下混凝土冻融损伤模型:

式中:D为相对动弹模量损失率,D0为初始损伤量,E0为受冻融时混凝土弹性模量,N为冻融循环次数,β,α为材料参数,σmax为最大静水压力。
该模型以Power静水压力理论为基础,综合考虑材料特性、降温速率与降温幅值等影响因素,预测结果与试验数据吻合度高。但该模型没有考虑到尺寸对混凝土温度场的影响;且最大静水压力以显式出现,不便于应用;而且材料参数的求解需要利用混凝土抗拉试验,实际工程中混凝土抗拉试验并不常见。考虑以上三点,本文以蔡昊模型为基础,考虑混凝土尺寸效应,结合理论推导和试验研究,给出可用于实际混凝土结构的冻融损伤模型。
1.1材料参数的求解
根据β,α的定义:
(2)
式中:σt,εt混凝土发生损伤局部化之前的最大应力及应变。对于普通混凝土,σt可取为应力为80%混凝土抗拉强度;对于高强混凝土,σt取为应力为90%混凝土抗拉强度。E0,Et为混凝土初始弹性模量和应变为εt时的切线模量。
基于大量混凝土抗拉性能试验,得回归公式[9]:
(3)
文献[10]给出较准确的混凝土受拉应力应变曲线:
x≤1y=1.2x-0.2x6
(4)

(5)
将式(3)代入式(5)得:
(6)
将式(3)和(6)代入εt=0.684εt,p,σt=0.8ft得:
(7)
在受拉曲线上升段,由式(4)可得:
(8)
求导可得:
(9)
分别令ε=0,ε=εt,并代入式(3), (6)可得:
(10)
将式(10)、(6)和(3)代入式(2),可求得λ=0.975,该结论表明,冻融试验计算得到的λ趋于常数。根据李金玉,宋玉普等[7-8,11-22]关于普通混凝土标准冻融试验中的冻融循环次数及混凝土抗压强度,取初始损伤量D0=0,代入λ值,利用式(1)~(10),反推得到不同冻融循环次数下的动弹模量损失率D,同以上试验中得到的相对动弹模量损失率对比发现,D的值对系数λ的取值比较敏感。λ值波动±0.01将引起D发生∓5%的变化。考虑混凝土的离散性以及推导过程近似公式的误差积累,需对参数λ进行调整和修正,以得到最合适的λ值。λ同混凝土抗压强度和水灰比的关系如图1和图2。图1、2证明了上述推论:λ同水灰比和抗压强度并没有明显的相关性,而是围绕一常数波动。
拟合后有λ=0.932,取D0=0,代入式(2)可得:
(11)
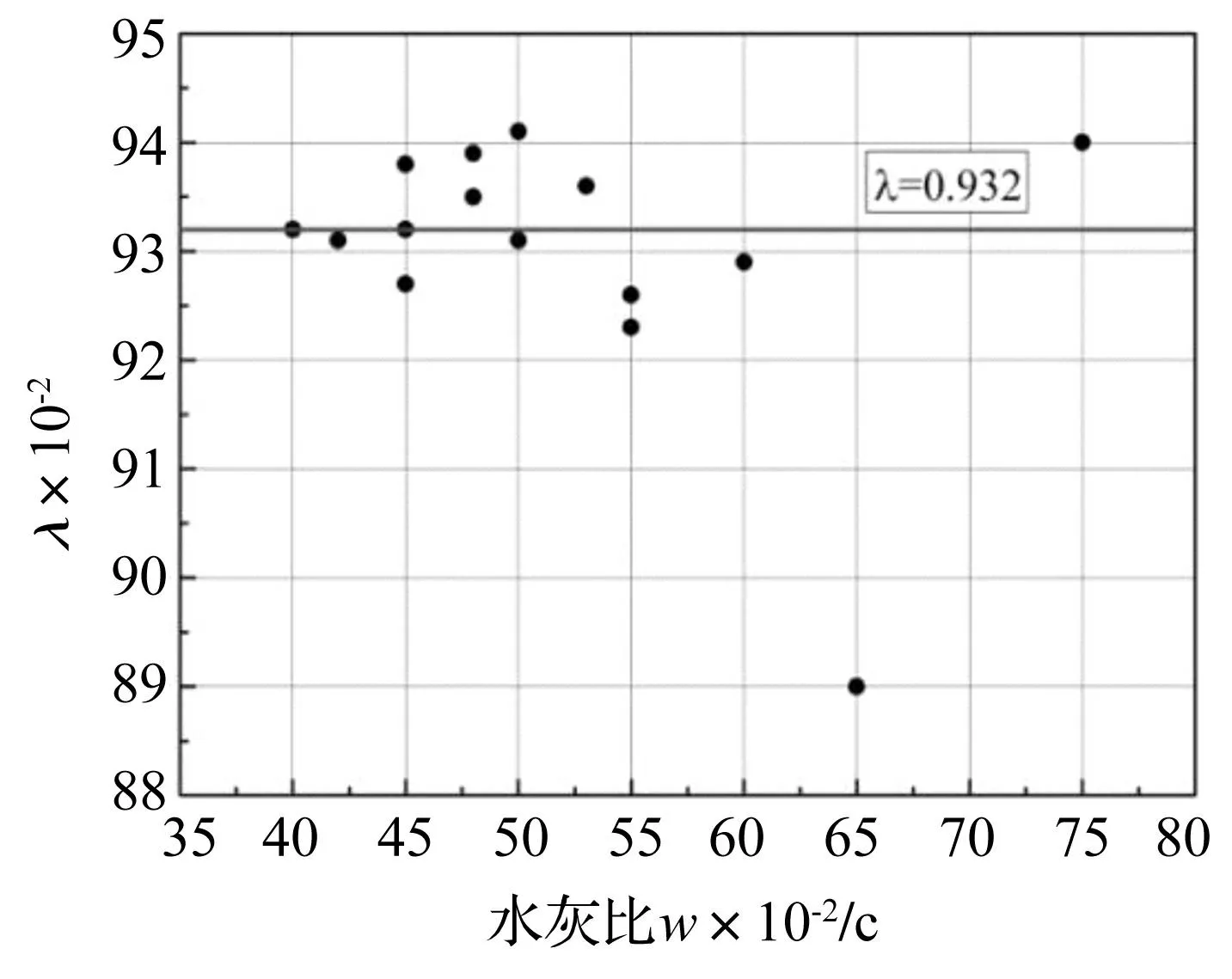
图1 水灰比w/c同λ的关系Fig.1 The relationship between water-cement ratio w/c and λ
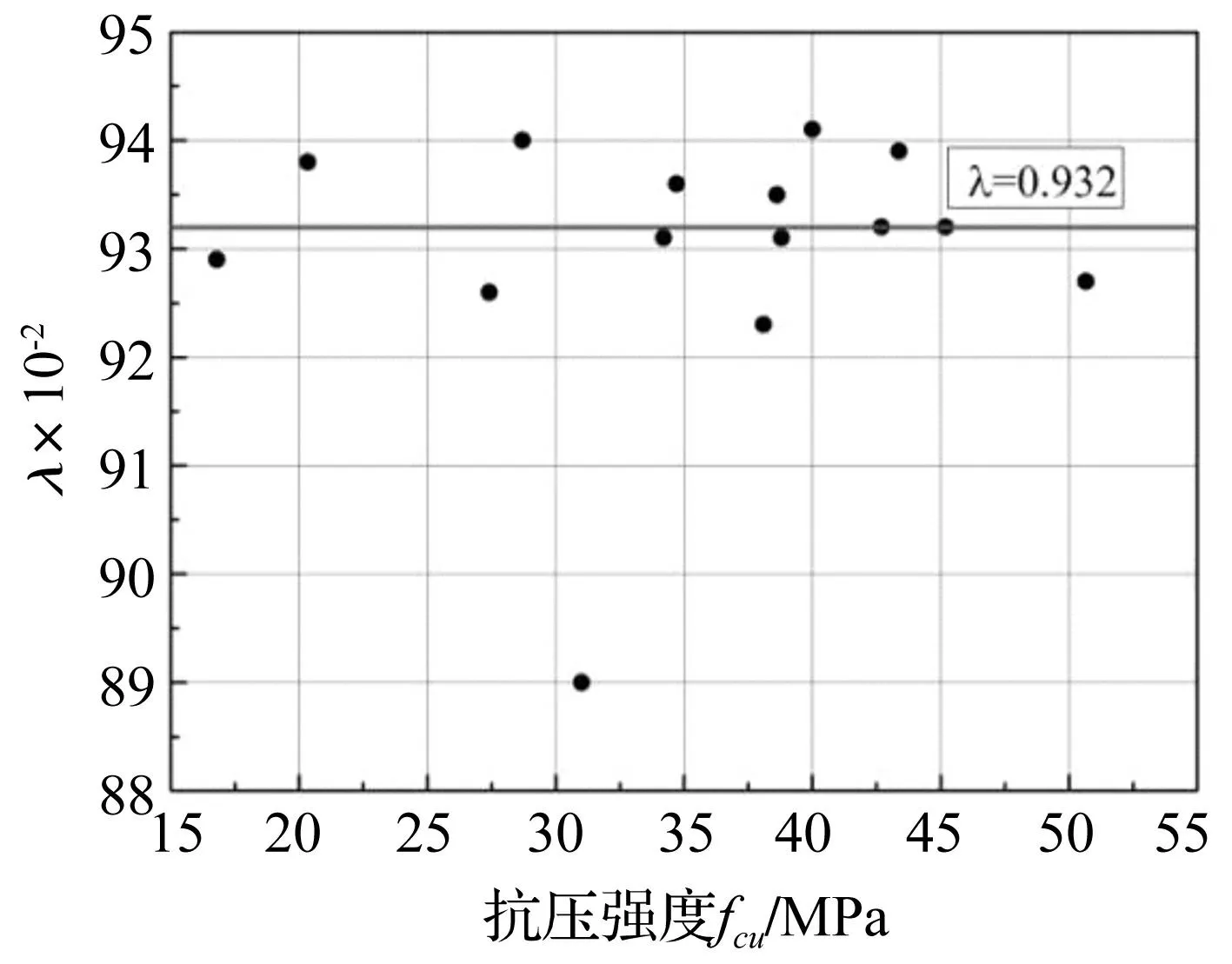
图2 抗压强度fcu同λ的关系Fig.2 The relationship between the compressive strength fcu and λ
1.2最大静水压力σmax的求解
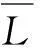

(12)
(13)

(14)

孔溶液的动力黏滞系数η可用水的动力黏滞系数近似替代。在0 ℃~-15℃水的动力黏滞系数见表1[8]所示。

表1 0 ℃~-15℃下水的动力黏滞系数
Powers曾给出水泥石渗透系数K同水泥石毛细孔隙率之间的经验关系式[6]:
K=3 350ε3.6×10-21
(15)
式中:ε为水泥石毛细孔隙率,根据ε的定义有:

式中:ρa为毛细孔所占的混凝土体积的百分比;ρc为水泥浆体所占的混凝土体积的百分比;ρw为负温下未结冰孔溶液体积占原孔溶液体积的百分比。
将混凝土试块放在水中浸泡4天,取出擦干表面,称重后放入100℃烤箱中烘烤至恒重,计算可得到毛细孔体积占混凝土体积的百分比ρa。水泥浆体所占混凝土体积的百分比ρc可以由混凝土配合比计算得到。

根据Powers的静水压力理论,U取最大值Umax时,静水压力最大,即Pave=σmax。Bager[25]用低温差热法研究了水泥石孔隙水冻融过程。通过量测不同水灰比的水泥石在冻结过程中释放的热量,得到的结论是:在饱水情况下,孔溶液大量结冰的区间主要集中在-7℃~-10℃和-23℃~-42℃。在实际工程中,很少会遇到-23℃~-42℃这样的低温,所以-7℃~-10℃应作为主要研究的温度区间。
2试验研究
设计不同水灰比试件9组,每组5个,水灰比分别为:0.35,0.4,0.45,0.48,0.52,0.58,0.6,0.65,0.7。测量温度区间设定为0℃~-17℃,分别测定在0℃,-5℃,-10℃,-15℃时相对结冰量,计算得到不同温度时的U。
2.1混凝土原材料及配合比
本试验配制了9组不同水灰比混凝土试件,水泥采用普通硅酸盐水泥(425#),砂粒径小于2.5 mm,粗骨料为粒径10~20 mm碎石,表2为单位体积混凝土配合比及性能指标。

表2 混凝土配合比及性能指标
2.2试验方案[23-24]
按照不同配合比分别设计100 mm×100 mm ×150 mm试块,试件制作时预埋6块铜网电极,试件制作如图3。将养护28天的试件在水中浸泡至恒重后取出,冻融在环境模拟试验室中进行,温度设定为0℃~-17℃。
首先将饱水后的试件在0℃冻融箱中放置24小时,测量其在0℃时的电阻,然后依次降低冻融室中的温度分别至-5℃,-10℃,-15℃,并在每一温度下停留24小时,测量其电阻(注:停留24小时是为了保证试块的温度均到达测点温度)。

图3 用于测量结冰速率的混凝土试块Fig.3 Concrete blockused to measure the freezing rate
2.3结冰速率测量原理

(16)
式中:hc为电流通过混凝土试件的长度;hs为电流通过孔溶液的等效长度;Sc为电流通过混凝土试件的面积;Ss是电流通过孔溶液的等效面积;σc为混凝土试件导电率;σs为孔溶液导电率。
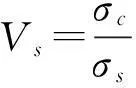
(17)

(18)
2.4试验结果及分析
限于篇幅,本文仅以水灰比为w/c=0.4和w/c=0.6为例进行说明:
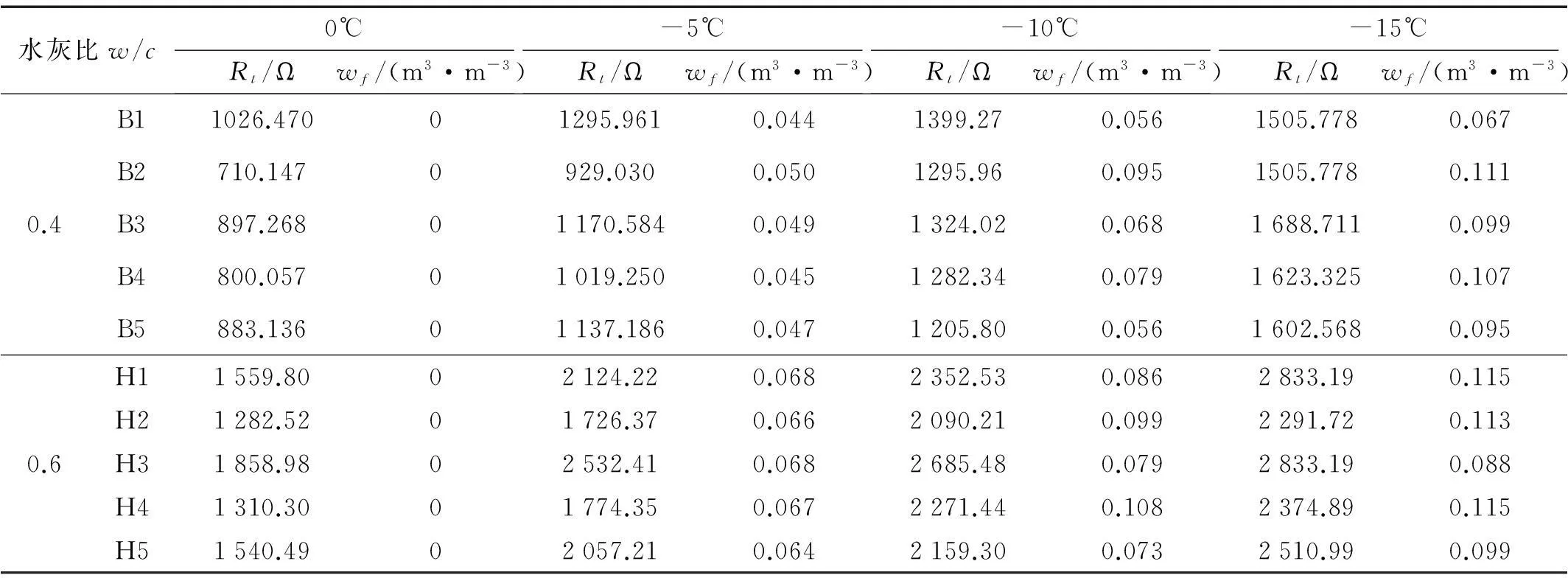
试验测得水灰比为w/c=0.4和w/c=0.6的试件在不同温度下电阻以及由式(18)计算得到的单位体积的水泥浆体内冰的孔溶液体积wf见表3。以温度t为横坐标,wf为纵坐标,计算得到w/c=0.4和w/c=0.6的试件在不同温度下的单位体积的水泥浆体内冰的孔溶液体积wf见图4。用泰勒级数拟合,发现当x的最高次为2次时相关系数即可达到0.95以上,计算精度高。

图4 不同温度下的单位体积混凝土内结冰孔溶液体积wfFig.4 Ice volume of Per cubic meter of concrete under different temperature
从图4可知,不论是w/c=0.4组试块还是w/c=0.6组试块,0℃~-10℃区间内混凝土结冰速率都相对于-10℃以下的温度区间大,故此温度区间冻害较大。这一试验结论同李金玉等得到的最低温度对普通混凝土抗冻性能影响的试验结果相同。因此,对普通混凝土抗冻耐久性的研究应主要集中在0℃~-10℃区间内。图4中的曲线表明,混凝土内部大量结冰集主要集中在0℃~-5℃区间,尤其是w/c=0.6试验组试块,比Bager用低温差热法测得的-7℃~-10℃区间要高,这主要是因为本试验中采用的是混凝土试块,而Bager低温差热法用的是水泥净浆,相比于水泥净浆,混凝土中不仅有水泥浆体内部孔隙,而且在粗骨料和砂浆的界面上存在着不规则的初始裂缝,初始裂缝的直径相对毛细孔孔径大,内部的孔溶液冰点温度相对较高,导致混凝土的大量结冰温度区间要高于纯水泥净浆。
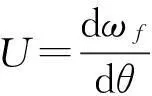
(19)
表3中的数据代入(19)可以得到w/c=0.4和w/c=0.6的试件在0℃~-5℃以及-5℃~-10℃区间的单位体积的水泥浆体内冰的孔溶液结冰速率U(-10℃~-15℃区间计算得到的U较以上两个温度区间明显偏小,未予列出)如表4。
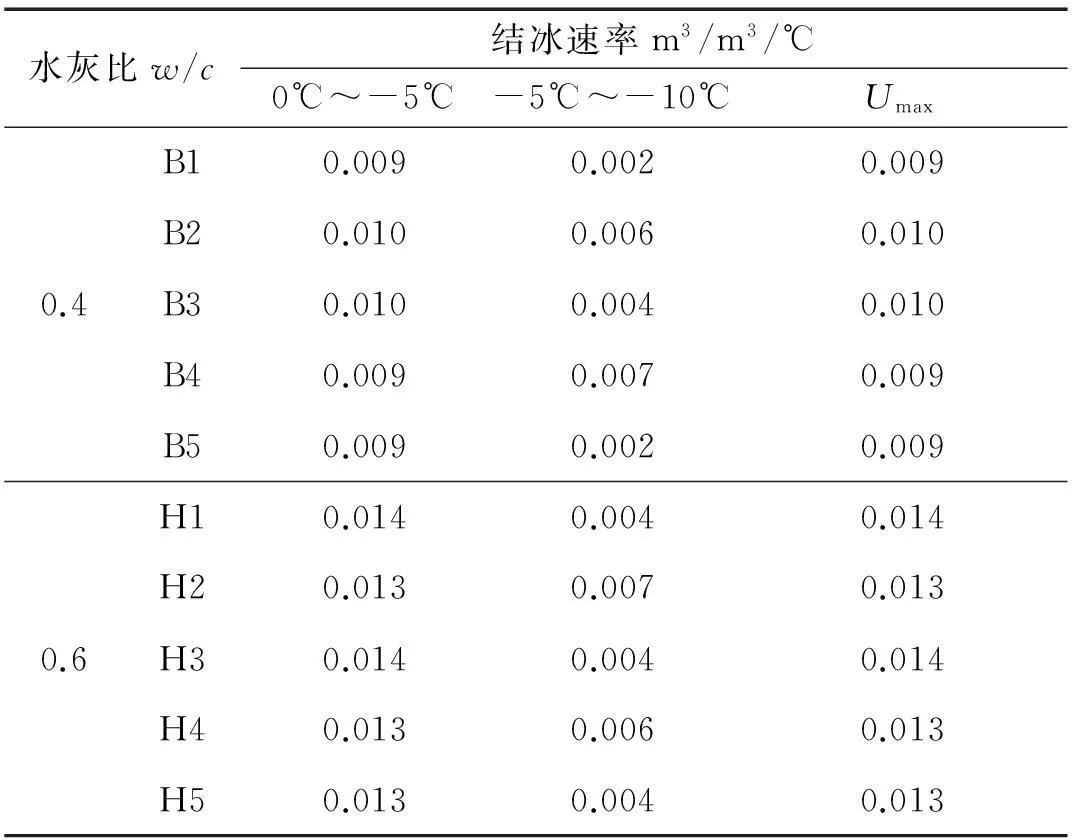
表4 单位体积混凝土内冰的孔溶液结冰速率
如表4所示,混凝土内结冰速率最大值主要集中在0℃~-5℃区间,比较到w/c=0.4和w/c=0.6的试件也可以发现,当水灰比较大时,区间更为明显,隙水液面弯曲小,饱和蒸汽压越大,0℃~-5℃区间内结冰速率增长较-5℃~-10℃冰点就越高[26],这是由于水灰比越大,不仅混凝土内部孔隙较多,而且直径较大的孔隙偏多,而毛细孔直径越大,孔所以在0℃~-5℃区间内结冰的孔溶液相对较多,该区间内的结冰速率也相对增长较快。

Umax=0.027 8(w/c)2-0.007 3(w/c)+0.007 7 (20)

图5 单位体积的混凝土内Umax同w/c之间的关系Fig.5 The relationship between Umaxof Per cubic meter of concrete and w/c
3混凝土结构冻融损伤模型
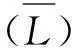
式(21)的物理模型为Powers水泥石结构简化模型,没有考虑到混凝土结构内部温度场的不均匀分布,因此,要将式(21)应用于实际中的混凝土结构,还需要考虑到混凝土内部温度场的分布情况。考虑温度场分布,式(21)变换得到式(22)。
(21)
(22)
式中:V为处于冻融环境中的混凝土结构的体积;Vd为受冻融影响的混凝土的体积,根据上述试验结论,可取为最低温度低于-5℃,最高温度大于0℃的混凝土体积。
4试验验证
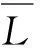

图6 气候模拟试验室内部温度Fig.6 Temperature in the climate simulation laboratory

试件编号尺寸mm×mm×mmβ/(m2·s-1)L/μmrb/μm试验测得的相对动弹模量损失量/%(冻融循环次数N)S-1100×100×4001.476×10-66561198.13(50)15.13(100)30.4(150)35.5(200)S-2150×150×4001.476×10-68661436.21(15)13.16(30)23.43(50)39.5(75)
采用有限元软件ANSYS热分析模块对混凝土冻融进行模拟,得到内部温度场[29]的分布和受冻融影响的混凝土的体积Vd。试件6个表面均受到如图6中的变化的温度荷载作用,初步的模拟分析显示,对于两试块,底面和顶面上的温度荷载对混凝土试块内部温度场的影响很小,为方便计算,将两试块分别简化为100 mm×100 mm和150 mm×150 mm,四面受变化的温度荷载的平面模型。试块初始温度为0℃,模拟发现经过3~5个循环后,内部温度趋于稳定的周期性变化。第5个循环结束时混凝土试块S-1内部温度场分布如图7。S-1试件由表及里不同深度处温度变化如图8(图中h0到h8分别代表的深度为0 mm,5 mm,10 mm,15 mm…45 mm)。

试验值和预测模型对比结果见图9。

图7 第5个循环结束时S-1温度场分布Fig.7 The temperature distribution in S-1 at the end of 5th Cycle

图8 S-1试块不同深度处的温度变化Fig.8 The temperature distribution in S-1 at the different depth

图9 预测模型与试验值对比Fig.9 Thecomparation between the predictive value and test value
从图9可知,预测模型与试验能够较好的吻合,尤其是在动弹模量损失量不大的时候,当动弹模量损失量超过30%之后,预测模型同试验值稍有偏差,主要是因为损伤累积,导致内部孔隙结构发生变化,平均孔径和气孔间隔系数有所增加[5],而在预测模型中很难考虑到该变化,所以预测值会有所偏小,但仍在可接受的范围之内。
5结论
本文指出了目前构件层次的混凝土冻融试验没能考虑混凝土所处的外部冻融环境的差别及内部温度不均匀分布,而简单以冻融循环次数为物理损伤指标的不合理性。通过理论推导及试验研究,主要得到如下结论:
(1)基于静水压力理论和损伤力学的蔡昊模型中的材料参数趋于常数,同水灰比和抗压强度并无明显相关性。
(2) 水灰比对冻融条件下混凝土最大结冰速率所处的温度影响显著,水灰比越大,最大结冰速率时所处的温度越高。
(3)冻融条件下混凝土结冰速率同水灰比二次方成线性关系,表明水灰比是决定混凝土抗冻性能的最主要因素。
(4)考虑冻融条件下混凝土结构构件内部温度场的不均匀分布,并通过有限元软件ANSYS对其进行模拟,获得改进后的冻融损伤模型,其与试验结果吻合较好,可应用于混凝土结构与构件的冻融损伤评估。
参 考 文 献
[1] 陈婷.冻融循环与氯盐侵蚀耦合作用下预应力混凝土构件劣化性能研究[D].镇江:江苏大学,2011.
[2] 周禹.钢筋锈蚀与冻融作用下钢筋混凝土梁的抗弯性能[D].沈阳:沈阳建筑科技大学,2009.
[3] 赵霄龙,卫军,黄玉盈. 混凝土冻融耐久性劣化与孔结构变化的关系[J],武汉理工大学学报,2012,24(12):14-17.
ZHAO Xiao-long, WEI Jun, HUANG Yu-ying. Relationship between pore structure change of concrete and its frost durability degradation[J].Journal of Wuhan University of Technology,2012,24(12):14-17.
[4] 李曙光,陈改新,鲁一晖.基于微裂纹定量分析的混凝土冻融损伤评价方法[J].水力发电学报,2013,32(3):207-212.
LI Shu-guang,CHEN Gai-xin,LU Yi-hui.Evaluation method for freezing-thawing damage in concrete based on quantitative microcrack analysis[J], Journal of Hydroelectric Enineering,2013,32(3):207-212.
[5] Powers T C. A working hypothesis for further studies of frostre sistance[J]. Journal of the ACI, 1945, 16(4): 245-272.
[6] Powers T C. The air requirement of frost-resistant concrete[J].Proceedings of the Highway Research Board, 1949, 29: 184-211.
[7] 李金玉,曹建国,徐文雨,等.混凝土冻融破坏机理的研究 [J].水力学报,1999(1):41-49.
LI Jin-yu, CAO Jian-guo, XU Wen-yu. Stydy on the mechanism of concrete destruction under frost action [J]. Shuili Xuebao,1999(1):41-49.
[8] 蔡昊.混凝土抗冻耐久性预测模型[D].北京:清华大学,1998.
[9] 过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2012.
[10] 过镇海,张秀琴.混凝土应力-应变全曲线的试验研究[J].建筑结构学报,1982,3(1):1-12.
GUO Zhen-hai,ZHANG Xiu-qin.Experimental investigation of complete stress-deformatlon curves of conerete in tension[J].Journal of Building Structures,1982,3(1):1-12.
[11] Penttala V. Surface and internal deterioration of concrete due to saline and non-saline freeze-thaw loads[J]. Cement and Concrete Research, 2006,36:921-928.
[12] 商怀帅,宋玉普,覃立坤.普通混凝土冻融循环后性能的试验研究[J].混凝土与水泥制品,2005,(2):9-11.
SHANG Huai-shuai,SONG Yu-pu,QIN Li-kun.Experimental study on the performance of plain concrete after freeze-thaw cycles[J].China Concrete and Cement Products,2005,(2):9-11.
[13] 施士升.冻融循环对混凝土力学性能的影响[J].土木工程学报,1997,30(4):35-42.
SHI Shi-sheng.Effects of freeze-thaw cycles on the mechanical properties of concrete[J],China Civil Engineering Journal,1997,30(4):35-42.
[14] 梁黎黎.冻融循环作用下混凝土力学性能试验研究[J].混凝土,2012,(3):55-57.
LIANG Li-li.Study on concrete compression performance under freeze-thaw cycles[J].Concrete,2012,(3):55-57.
[15] 程红强, 张雷顺, 李平先.冻融对混凝土强度的影响[J].河南科技,2003,21(2):214-216.
CHENG Hong-qiang,ZHANG Lei-shun,LI Ping-xian.The influence of freeze-thaw to concrete strength[J].Henan Science,2003,21(2):214-216.
[16] 覃立坤,宋玉普,陈浩然,等.冻融循环对混凝土力学性能的影响[J].岩土力学与工程学报,2005,8(增刊1):5058-5053.
QIN Li-kun,SONG Yu-pu, CHEN Hao-ran,et al.Influence of freezing and thawinb cycle on mechanical properties of concrete[J].Chinese Journal of Rock Mechanics and Engineering,2005,8(Sup1):5058-5053.
[17] 苏昊林,王立久.混凝土冻融耐久性量化分析[J].混凝土,2010,247(5):1-6.
SU Hao-lin,WANG Li-jiu. Quantitative analysis of freeze-thaw durability o f concrete[J].Concrete,2010,247(5):1-6.
[18] 唐光普,刘西拉.基于唯象损伤观点的混凝土冻害模型研究[J].四川建筑科学研究院,2007,33(3):138-143.
TANG Guang-pu,LIU Xi-la.A study on concrete frostmodel in view of phenomeno logical damage theory[J]. Sichuan Building Science,2007,33(3):138-143.
[19] 徐晓巍.不同环境下混凝土冻融试验标准化研究[M].杭州:浙江大学,2010.
[20] 尚怀帅.引气混凝土冻融循环后多轴强度的试验研究[D].大连:大连理工大学学报,2006.
[21] 卫军,李斌,赵霄龙.混凝土冻融耐久性的试验研究[J].湖南城市学院学报:自然科学版,2003,24(6):1-5.
WEI Jun,LI Bin,ZHAO Xiao-long. Experimental studies of freeze-thaw durability of concrete[J].Journal of Hunan City University:Natural Science,2003,24(6):1-5.
[22] 祝金鹏,李术才, 刘宪波,等.冻融环境下混凝土力学性能退化模型[J].建筑科学与工程学报,2009,26(1):62-67.
ZHU Jin-peng,LI Shu-cai,LIU Xian-bo,et al.Mechanical property deterioration model for concrete in environment with freezing-thawing[J]. Journal of Architecture and Civil Engineering,2009,26(1):62-67.
[23] 李美利.混凝土潮湿养护效率的电阻率评价方法研究[D].重庆:重庆大学,2011.
[24] 钱觉时,徐姗姗,李美利,等.混凝土电阻率测量方法与应用[J].山东科技大学学报:自然科学版,2010,29(1):37-42.
QIAN Jue-shi,XU Shan-shan,LI Mei-li, et al.The measurement and application of resistivity for concrete[J].Journal of Shandong University of Science and Technology:Natural Science,2010,29(1):37-42.
[25] 段安.受冻融混凝土本构关系研究和冻融过程数值模拟[D].北京:清华大学,2009.
[26] 郭成举.混凝土的冻害机制[J].混凝土与水泥制品,1982:9-19.
GUO Cheng-ju.Degradation mechanism due to freezing and thawing cycle of concrete [J].China Concrete and Cement Products, 1982:9-19.
[27] DL/T 5150—2001,水工混凝土试验规程[S].北京:中国电力出版社,2001.
[28] 刘光廷,黄达海.混凝土湿热传导与湿热扩散特性试验研究[J].三峡大学学报:自然科学版,2002,24(2):97-100.
LIU Guang-ting,HUANG Da-hai.Experimental study on thermal conductivity and diffusivity of moist concrete(Ⅱ)-experimental result and analysis[J].J of China Three Gorges University:Natural Sciences,2002,24(2):97-100.
[29] 章熙民,任泽霈,等.传热学[M].北京:中国建筑工业出版社,2001.
Experimental study on freeze-thaw damage model for concrete structures and membersbased on material
ZHENGShan-suo,WANGFeng,FUXiao-liang,WANGZi-sheng,GANChuan-lei
(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)
Abstract:Based on the Cai Hao model, through the theoretical derivation and the summing up of the freezing and thawing test data of material, the calculation method of maximum hydrostatic pressure in the model was improved. 9 groups of material tests were conducted to establish the fitting relationship between the water-cement ratio of concrete and the maximum freezing rate, and to derive a simplified analytic calculation formula for maximum hydrostatic pressure. The ANSYS finite element software was used to simulate the temperature field on component sections and an improved freezie-thaw damage model with consideration of the temperature distribution was proposed. 2 groups of experiments were implemented to verify the accuracy and reliability of the improved model. The results show that the revised freeze-thaw damage model using dynamic elastic modulus as a physical damage index can provide theoretical support to the freeze-thaw damage mechanism study of RC structures and members.
Key words:reinforced concrete (RC) structure; freeze-thaw; water cement ratio; temperature field; freezing rate; relative dynamic modulus
中图分类号:TU375
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.03.028
通信作者汪锋 男,硕士生,1988年生
收稿日期:2014-06-24修改稿收到日期:2015-01-30
基金项目:国家科技支撑计划(2013BAJ08B03);国家自然科学基金(50978218;51108376);教育部高等学校博士学科点专项科研基金(20136120110003);陕西省科研项目(2012K12-03-01;2011KTCQ03-05;2013JC16)
第一作者 郑山锁 男,教授,博士,博士生导师,1960年生
邮箱:zhengshansuo@263.net
