微小间隙空气静压主轴角刚度分析与实验**
2016-04-07王宝瑞
周 亮 王宝瑞 阳 红
(中国工程物理研究院机械制造工艺研究所,四川 绵阳 621900)
微小间隙空气静压主轴角刚度分析与实验**
周 亮 王宝瑞 阳 红
(中国工程物理研究院机械制造工艺研究所,四川 绵阳 621900)
通过综合气体运动方程、连续性方程和状态方程,建立小孔节流气体润滑主轴数学模型。采用有限单元法、超松弛迭代法和比例分割法对雷诺方程进行离散求解,解决了微小间隙空气静压主轴跨尺度微偏转的气膜压力分布数值计算难题。进行静态角刚度测试实验,验证了所提方法的有效性。
空气静压主轴;角刚度;有限元分析;小孔节流
静压主轴是超精密机床实现精密回转运动的关键部件,它采用流体润滑技术,借助于气膜或液膜来分开运动件与支承件,以减小摩擦,提高运动稳定性。在超精密加工机床中,静压主轴是电动机与刀具或工件装夹机构联系的纽带,对机床的加工精度起着决定性影响。
目前在静压主轴方面的研究主要集中在刚度(径向刚度、轴向刚度、前端刚度)、回转精度、动态特性以及热稳定性等方面。如姚俊等介绍了各种机床主轴回转精度测量方法及其原理以及测量数据的处理和误差分析方法[1]。彭万欢等采用两点测量法深入分析了超精密空气静压主轴回转误差测试过程中偏心的影响和作用原理[2]。陈东菊等研究了气体稀薄效应对轴承承载力和刚度的影响,为微尺度下轴承性能的研究提供了一定的理论依据[3]。在主轴性能研究中,其轴线抵抗偏摆的能力——角刚度是一个很重要的指标。轴线偏摆不仅会影响主轴的回转精度;在主轴运动过程中,如果角刚度较小,还可能产生摆振。然而,国内对角刚度的研究还不够深入。侯国安等在研究静压主轴动态特性时讨论了水平方向角刚度的理论计算方法,但未考虑实际工况下切削力以及重力作用存在的初始偏心对角刚度的影响,没有给出详细的验证说明[4]。安晨辉等通过旋转欧拉方程研究了主轴稳定性,具有借鉴意义,但也没有验证其方法的合理性[5]。杨福兴[6]、夏欢[7]以及徐灏[8]等人结合轴承尺寸,分别给出了通过径向刚度和轴向刚度计算角刚度的经验公式,齐乃明等[9]推导了双列径向轴承在无偏心状态下的角刚度计算;但此类公式不含角度参数,不能计算变角度情况下的角刚度。
目前,对静压主轴角刚度的研究,通常仅计算了无重力作用无偏心状态下的角刚度,与实际工况差异较大,也没有对角刚度进行实验测试验证,没有对角刚度的形成机理进行深入系统的研究。本文在气体运动方程、连续性方程和状态方程的基础上,引入重力和初始偏心距,建立起实际工况下小孔节流气体静压主轴径向轴承和止推轴承数学模型,采用有限单元法、超松弛迭代法和比例分割法进行离散、求解和计算气膜内压力分布,从而解决微小气膜间隙下微偏转跨尺度的数值计算问题。最后通过实验测试静态条件下静压主轴的角刚度,验证数值计算的准确性。
1 空气静压主轴角刚度建模
1.1 空气静压主轴角刚度定义
空气静压主轴依靠气体静压效果实现支承和限制主轴转子位置和姿态。径向刚度和轴向刚度评价了转子X、Y方向的位置稳定性,与此类似,角刚度评价了转子姿态稳定性。因此,与刚度定义类似,角刚度为静压主轴力矩与偏摆角度的比值,计算式为
kθ=M/θ
(1)
式中:kθ为角刚度;M为主轴总力矩;θ为主轴偏转角。
主轴通常由径向轴承和止推轴承组成。如图1所示,为某T型结构的空气静压主轴模型。由于T型主轴结构非对称,其角刚度采用经验公式计算时误差会显著增大。因此,需采用有限元法来计算静压主轴的角刚度。

1.2 空气静压主轴角刚度理论建模

如图2所示,当T型轴绕过A点垂直纸面轴线发生微小偏转时,主轴受力可以简化为径向合力F1和止推力偶M(F2,F2’)。径向轴承力矩和止推轴承力矩可以分别计算,同时止推轴承产生的力矩可以投影为绕轴承圆盘中心的转动。主轴总力矩为
M=M1+M2=F1L+2F2Rsinα=F1L+2F2r
(2)
1.2.1 空气静压主轴径向轴承建模
对于径向轴承,其气膜厚度远小于其他两个方向的尺寸,通常情况下,厚度方向的压力和速度变化可以忽略;同时,当无转动或者转速很低时,雷诺数很小,与之相关的项可以忽略。经过简化,径向轴承的Reynolds方程无量纲化形式[10]为
(3)
(4)
式中:η为空气粘滞系数;l、hm分别表示无量纲化对应参考长度、气膜厚度;p0、pa、ρa分别表示供气压力、大气压力和大气密度;mr为单位时间流过节流孔的质量流量。
将气膜沿垂直方向切分展开,则压力分布近似为平面问题。将气膜研究域划分为三角形单元体集,如图3所示,则会产生对称边界、大气边界和节流孔边界三种边界条件。
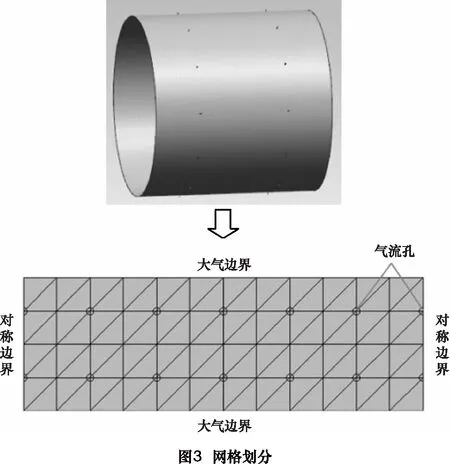
每个单元体内任意点压方都可由所在单元体的三节点压方表示,设插值函数为
f=Nifi+Njfj+Ntft
(5)

按照变分原理对雷诺方程进行处理,同时将式(4)和(5)代入雷诺方程式(3),对每个节点可以列写出一个方程,则整个研究域可以写出所有未知节点的方程,构成一个位置函数的矩阵方程:
KF=T
(6)
式中:F为待求节点压力函数,为n×1维列阵,K为n×n维刚度矩阵,是Ni、Nj、Nt函数的矩阵形式;T为n×1维列阵,是与边界条件和节流孔流量有关的非线性列阵。涉及到的流量项可按下式计算:
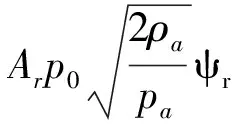
(7)
(8)
式中:Ar为节流面积;φ为流量系数,一般可取0.8; pd为节流孔出口压力; k为气体比热比,空气一般为1.4;其余同上。
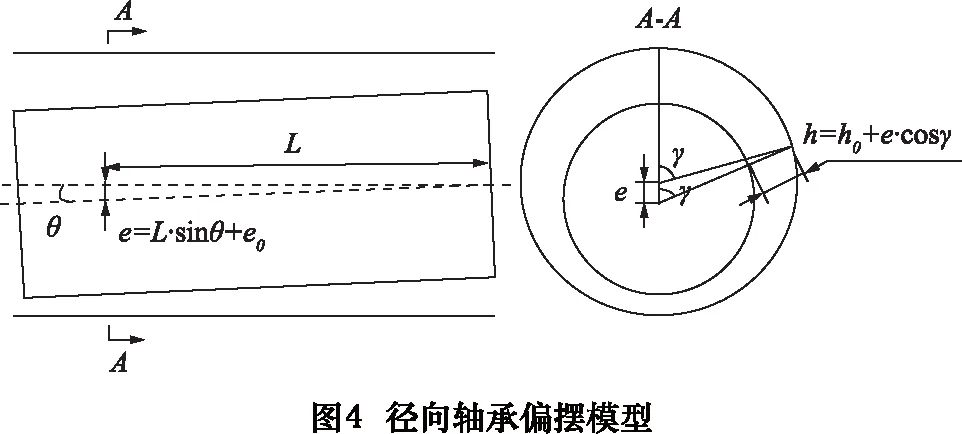
当主轴发生偏转后,气膜厚度h也是位置的函数,如图4所示。
h=h0+e·cosγ=h0+Lsinθ·cosγ+e0·cosγ
(9)
式中:h0为气膜平均厚度;γ为单元体与竖直方向夹角;e为偏心距;e0为初始偏心距;L为单元体至偏转中心距离;θ为主轴偏转角。
联立式(6)~(9)可以求解气膜内压力分布,但式(8)是非线性矩阵,故采用超松弛迭代法求解方程。若迭代后精度不满足要求,则采用比例分割法计算节流孔处第i+1次迭代压方初始值,如公式(10)。
(10)
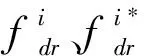
求得气膜压力分布后,整个主轴的承载W1和力矩M1计算式为
(11)
(12)
式中:m为单元体总个数。
1.2.2 空气静压主轴止推轴承理论建模
与径向轴承类似,止推轴承气膜厚度方向的压力和速度变化可以忽略。静态时,止推轴承的Reynolds方程无量纲化形式[10]为
(13)

(14)
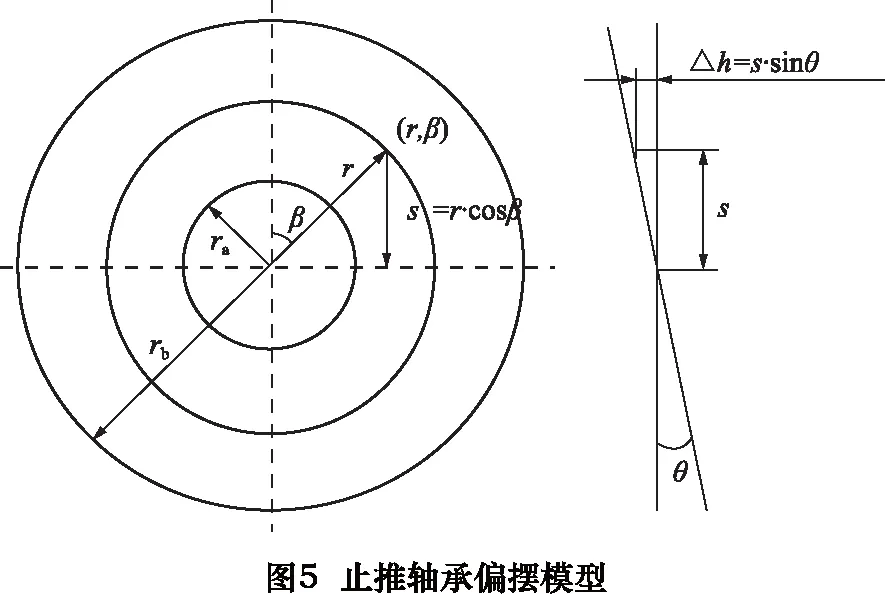
式(14)与式(3)十分相似,对式(14)的处理与式(3)相同。止推轴承通常为圆盘形,止推盘偏转时,气膜厚度的变化如图5所示,(r,β)单元体上气膜厚度h为
h=h0+s·sinθ=h0+rcosβ·sinθ
(15)
式中:s为单元体与水平轴线的距离;β为单元体与竖直方向夹角:r为单元体所在圆半径;h0为止推气膜平均厚度;θ为主轴偏转角。
同样,用有限单元法求解止推轴承的承载W2与力矩M2的计算与径向轴承类似:
(16)
(17)
式中:m为单元体总个数。
2 空气静压主轴角刚度数值计算
2.1 空气静压主轴角刚度计算流程
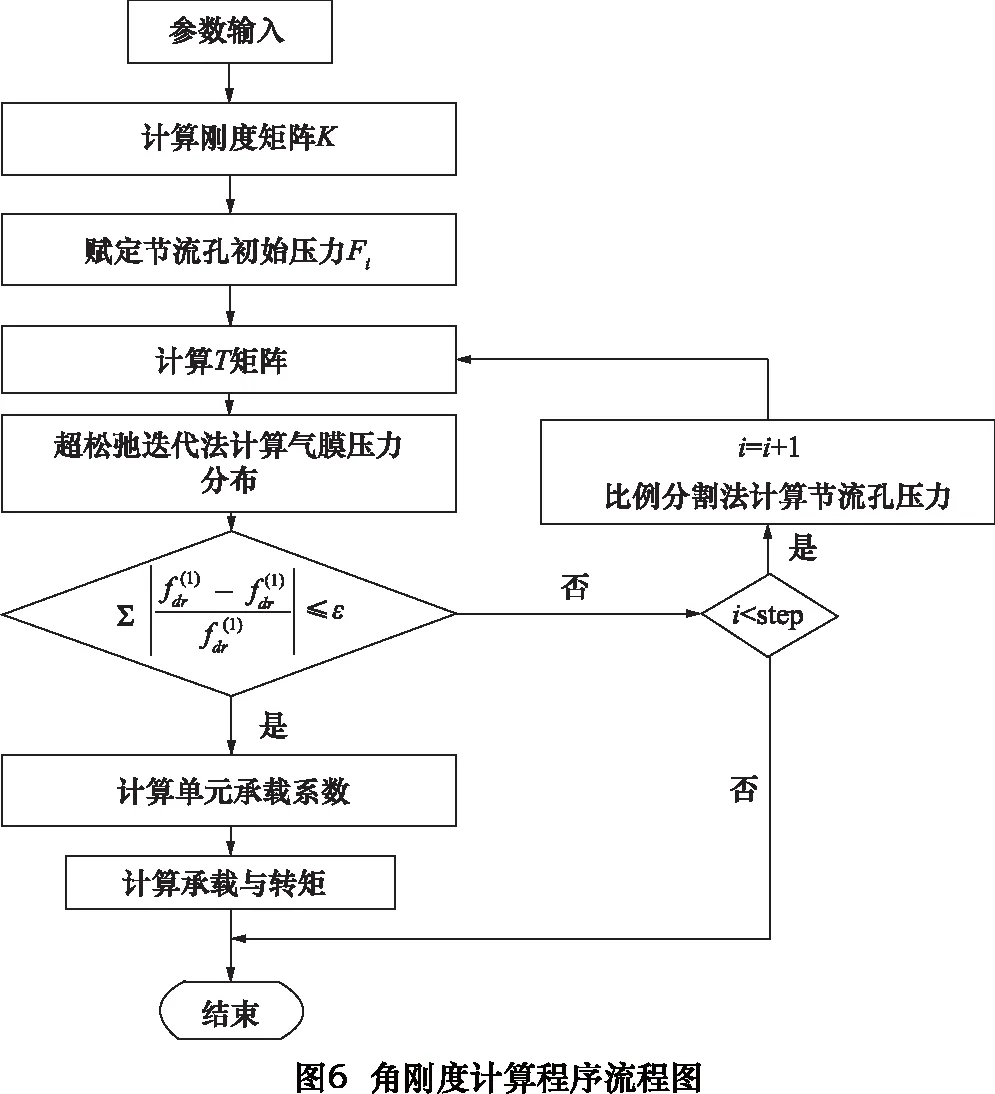
基于以上分析,我们在MATLAB 14.0基础上开发了角刚度计算程序,程序流程如图6所示。通过改变参数输入的大小,可以实现不同尺寸主轴径向轴承和止推轴承模型的快速建模和计算。
2.2 空气静压主轴角刚度计算结果
以某T型静压主轴为例,该主轴由两个径向轴承和一个止推轴承组成。径向轴承直径D=100 mm,宽度B=100 mm,气膜厚度h1=12 μm,两轴承间距L’=50 mm,双圈节流孔,每圈12孔,节流孔直径d=0.15 mm;止推轴承内径da=104 mm,外径db=228 mm,气膜厚度h2=10 μm,双圈节流孔,第一圈圆半径r1=68 mm,12孔,第二圈圆半径r2=98 mm,24孔,节流孔直径d=0.15 mm;整个转子部分约重28.1 kg。
基于编写的MATLAB程序,可以分别计算单个径向和止推轴承的承载和力矩。计算中,供气压力为0.5 MPa,出口压力为0.1 MPa,径向轴承划分为48×72个三角形单元,1 800个节点;止推轴承划分为30×128个三角形单元,2 304个节点。首先,当偏角θ0=0,计算出主轴在重力作用下的初始偏心距为e0;然后计算一定偏角θ下的径向和止推气膜上的角刚度kθ1、kθ2。对于上述主轴,由该程序计算可以得到初始偏心距e0≈1.1 μm,在偏角θ=1×10-5rad时,静压主轴径向轴承角刚度为kθ1=1.2×105N·m/rad,止推轴承的角刚度为kθ2=16.4×105N·m/rad,故整个静压主轴的角刚度kθ=kθ1+kθ2=17.6×105N·m/rad。
2.3 经验公式计算
上述主轴设计的径向刚度为405 N/μm,轴向刚度为507 N/μm。文献[8-9]给出了通过径向刚度和止推刚度计算角刚度公式:
径向轴承的角刚度kθ1为
kθ1=k1B2/16
(18)
式中:k1为径向刚度,B为径向轴承宽度。
止推轴承的角刚度kθ2为
kθ2=k2((da+db)/2)2/8
(19)
式中:k2为轴向刚度;da、db为止推盘内外径。
由式(18)和式(19)可以求得该主轴的径向轴承角刚度kθ1=2.5×105N·m/rad,止推轴承角刚度kθ2=17.5×105N·m/rad,整个主轴角刚度kθ=kθ1+kθ2=20.0×105N·m/rad。
3 空气静压主轴角刚度实验测量
3.1 力矩—位移法测量角刚度
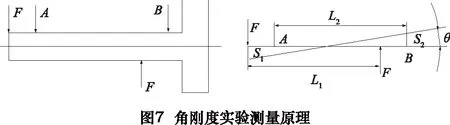
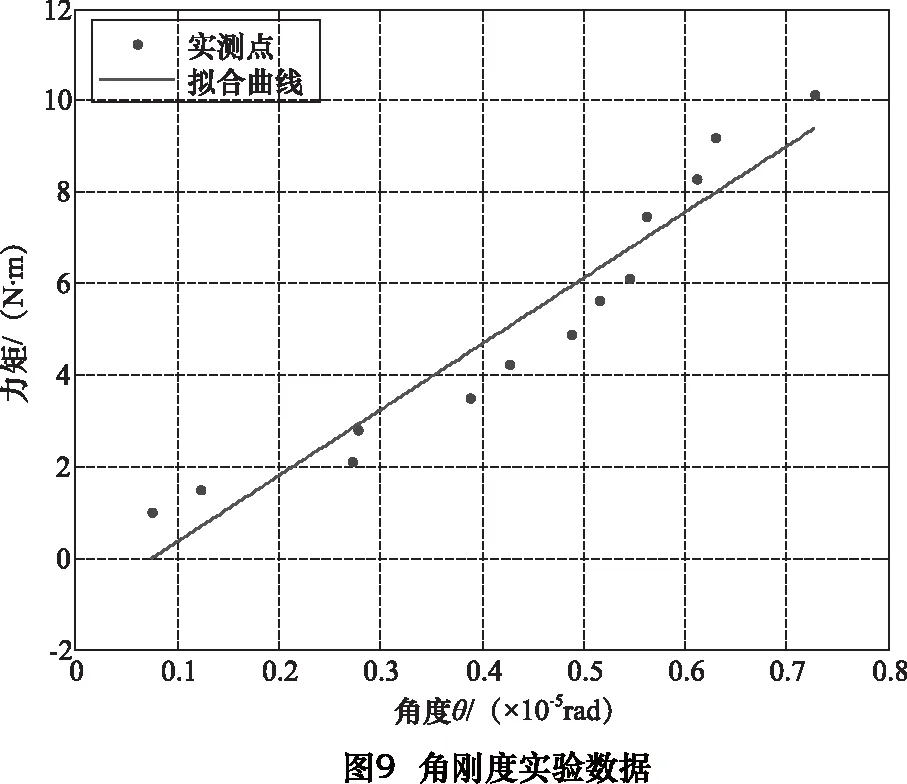
针对上述静压主轴,为了验证角刚度理论,设计了角刚度力矩—位移测量方法。实验原理如图7所示。力矩M=FL1,角度θ≈(s1+s2)/L2,角刚度kθ=M/θ。被测主轴和测量装置如图8所示。由于主轴转子部分在主轴座内部,无法直接加载和测量,故力矩加载通过过渡接头连接,位移测点分布在连接转子的测量片上。测量中保证两力大小相等,方向相反。通过实验,我们测得了该主轴在微小偏转时力矩与角度的关系(见表1),绘制了力矩—角度曲线,如图9所示。
采用最小二乘法通过MATLAB对实验数据进行一次项拟合,可以得到力矩—角度关系式为:
y=14.4x-1.091
(20)
对上式求导,可得该主轴在所测范围内的角刚度约等于14.4 N·m/rad。
表1 静压主轴力矩与角度测量

力矩/(N·m)01.0111.5022.1162.813角度/(×10-5rad)00.0740.1220.2720.278力矩/(N·m)3.4944.2574.9145.6256.144角度/(×10-5rad)0.3890.4260.4870.5150.544力矩/(N·m)7.4808.2999.20710.136角度/(×10-5rad)0.5610.6110.6300.728

3.2 理论计算与实验对比分析
对比实验结果与计算分析的数值,实验与数值计算结果相近。并且,有限单元法的计算结果比经验公式更接近实验测量值。同时,通过有限单元法可以计算任意偏角下的角刚度,弥补了经验公式的不足。
数值计算比实验结果偏大,主要有以下几方面的原因。一是数值计算将气膜内气体的流动均视为层流,而实际气流中存在紊流,此会导致数值计算结果偏大;二是主轴受力会产生形变,位移测量受形变误差影响使计算的偏角增大,此会导致测量的角刚度偏小;三是主轴结构尺寸在供气压力作用下也会改变,如小孔直径在较大供气压力作用下可能增大,四是由于传感器和仪器的粘滞特性,测量过程中存在间隙误差。角刚度测量的误差来源较复杂,目前测量的角刚度是各种因素作用下的综合角刚度。因此,在下一步的研究中,角刚度实验测量的误差分离将会是研究的重点。
4 结语
(1)采用有限单元法编写的角刚度数值计算方法与实验结果比较吻合,运用该算法能够实现各种尺寸结构的静压主轴角刚度计算。
(2)有限单元法比经验公式计算结果更接近实验测量值;并且有限单元法克服了经验公式无法确定角刚度与偏转角度的对应关系,具有更高的灵活性和更广的适应性。
(3)角刚度的测量存在复杂的误差来源,高精度的测量需要进行严格的误差分离。
[1]姚俊,王平. 主轴回转精度测量方法[J]. 制造技术与机床,2011(12):176-180.
[2]彭万欢,赵午云,陶继忠,等. 超精密空气静压主轴径向回转误差的测试研究[J]. 制造技术与机床,2008(10):55-58.
[3]陈东菊,周帅,杨智,等. 稀薄效应对空气静压止推轴承性能影响[J]. 四川大学学报,2016,48(1):194-199.
[4]侯国安. 流体静压支承对超精密金刚石车床动态特性影响的研究[D]. 哈尔滨:哈尔滨工业大学,2013.
[5]安晨辉,许乔,张飞虎. 空气静压主轴的压强分布与动态特性分析[J]. 纳米技术与精密工程,2009,7(5):459-468.
[6]杨福兴,董申. 超精密空气静压主轴静态性能的数值分析[J]. 机械设计与研究,2004,20(2):54-56.
[7]夏欢,吉方,陶继忠. 空气弹簧调平系统研究[J]. 现代制造工程,2012(11): 104-107.
[8]徐灏,邱宣怀,蔡春源,等. 机械设计手册[M]. 北京:机械工业出版社,1995.
[9]Qi Naiming,Li Zhongying,Yang Guojun,et al. Study on high stiffness gas bearing for precision centrifuger[J]. Journal of HarBin Institute of Technology,1998,5(4):47-50.
[10]刘暾,刘育华,陈世杰. 静压气体润滑[M]. 哈尔滨:哈尔滨工业大学出版社,1990.
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Analysis and test of angular stiffness on aerostatic bearing
ZHOU Liang, WANG Baorui, YANG Hong
(Institute of Mechanical Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621900, CHN)
The paper synthesizes gas motion equation, continuity equation and state equation, to establish mathematical model of orifice gas lubricated journal bearing. The Reynolds equation is discretized by the finite element method, then solved by the super relaxation iteration method and the proportional division method. The paper solves numerical problems of cross scale and micro deflection on small gas film clearance of aerostatic bearing spindle. Static angular stiffness experiments were carried out, which proves the validity of the proposed method.
aerostatic bearing spindle; angular stiffness; finite element analysis; orifice restriction
*国家自然科学基金(51305413);中物院科技专项资助(9120602)
TH133.35
A
10.19287/j.cnki.1005-2402.2016.12.006
周亮,男,1990年生,硕士研究生,主要研究方向为精密加工及测量。
(编辑 汪 艺)
2016-09-26)
161214
