第一部分:课堂实录
2016-04-05
第一部分:课堂实录
一、课堂引入:用问题激起相应的经验,构建数学活动.
师:前面我们学习过任意角的三角函数,下面我们通过几个问题来检测一下大家的掌握情况.
这些问题零散地分布于上一节内容即任意角的三角函数教材的例习题之中,比如人教版必修4第12页例1即求的正弦、余弦和正切值,但教材在处理过程中用了一句非常典型的话:易知∠AOB的终边与单位圆的交点坐标为在这里集中呈现,并不是让学生进行简单地重复,而是让学生交流这个“易知”背后的数学活动过程,这样不仅有利于激起对已有经验的回忆,更有利于新的经验的产生.
于是在学生纷纷表明完成并进行简单的组内交流后提出了问题:你是怎么求这些角与单位圆的交点坐标的?
看见学生还在边说边深思,老师决定帮他加上一把火:那它们的终边与单位圆的交点之间是什么关系?它们的坐标之间是什么关系?
生1继续:两个交点也关于原点对称,它们的坐标互为相反数.
(众生皆点头微笑)那么你们由此可以得出什么样的关系式?
除了少数同学在得到正切的关系时出了点小问题但也在小组交流时顺利得以解决,最后学生都得到了如下结果:

师:利用这样的方法,你还可以求出什么角的三角函数值?
二、深入探讨,将活动经验推广到一般化,通过归纳演绎,形成概念.
师:刚才的探讨中我们用到了三个特殊的角,大家有没有想一下,还有更多的角不可能这么特殊,我们能不能从更一般的角入手研究一下?
生2:刚才我发现任何一个锐角α将其终边绕原点逆时针方向旋转π弧度之后所得到的角,它的三角函数值与α之间都会有一定的关系.
在大家的鼓励下他写出了三个式子:
sin(π+α)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα.
大家的掌声还未落,又一个学生举起了手.
生3:我觉得这里的α不一定要是锐角,对任何一个角来说,这三个式子都成立.
众生愕愕,但看到老师鼓励的眼神,于是都表现出了探索的兴趣,纷纷在各小组内进行热烈地讨论.
随着讨论的进行,同学们的见解逐渐统一,生3的脸上也露出了自信的笑容.这时却还有一个同学还在低头默默地在纸上画着什么,于是老师示意:你还有什么不同的看法,能不能和大家一起分享一下?
生4:我觉得这个式子好像还可以强化一下.
以生3为代表的相当部分同学顿时都用一种惊讶的眼神看向了生4.
生4:既然是将角α将其终边绕原点旋转,那么不管按什么方向,旋转多少弧度,只要能使得到的角的终边和α的终边关于原点对称,那么这三个式子都应该成立!
老师看了一下顿时安静下来陷入了思考的同学们:大家好像都不反对你的看法,可问题是这样得到的角与α之间有什么样的关系呢?
生4:可以写为(2k+1)π+α,k∈Z(为方便叙述,下面的k都是整数).
师:你能把你得到的关系用等式表达出来吗?
生4在黑板上写出了相应的关系式:


众生沉思之时,生5站起来了:我觉得这几个式子还可以结合我们前面学过的公式一来理解,(2k+1)π+α的终边与π+α的终边相同,它们的三角函数值相等.
这一下其他学生也都表示了理解,纷纷点起头并露出了笑容.
师:看来他们两个人思考问题的出发点虽然不一样,但得到的结论却完全一样.在这个过程中他们所用到的知识和方法其实并不新鲜,都是大家在前面学习时遇到并用过的.所以我们在探求新的知识时不要局限于一种固定的角度,要敢于大胆地去尝试,很多有趣的东西在我们探索之初我们并不知道一定就会得到这么美的结果.
三、横向联系,尝试运用经验并进一步积累,强化概念的形成过程.
于是教室内在安静了几分钟之后再次陷入热烈的讨论之中,最后两个同学自告奋勇地上前代表他们所在组表述探究成果.

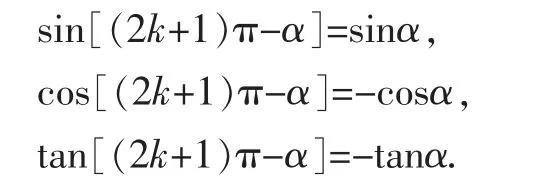
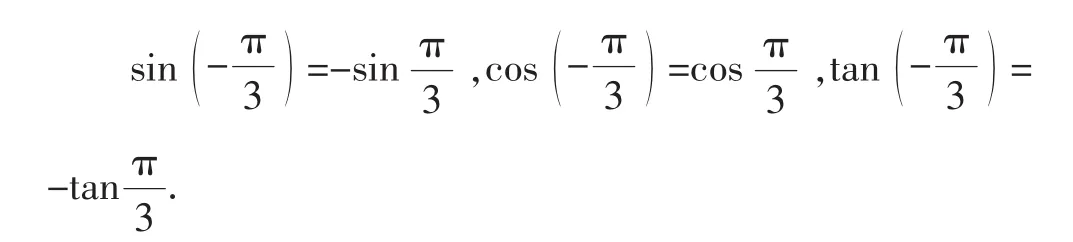

正在学生分享探索的喜悦时,老师又提出了问题:这些式子这么美,所以我们的前辈们就称它们为诱导公式.大家能否结合我们刚才的探索再思考一下:它们可能会有哪些用途?
生8:我想对于一个数值上很大的角,我们可以利用这些公式来求它的三角函数值.
生9:我觉得这倒在其次,只是求三角函数值我们也可以通过三角函数的定义来求,过程未必会比这复杂,我觉得关键还在于可以把一个数值上很大的角与一个锐角的三角函数值之间产生联系.
生10:我觉得这几组公式还提示了两个角的终边如果关于原点对称,关于x轴对称,关于y轴对称的话,就可以找到它们相应的三角函数值之间的关系.
同学们兴奋地随着他们的表述或沉思或轻声附和,这时老师出示了两组问题(教材上例题):下面就请大家用你们的聪明才智来发挥这几组公式的用武之地,看看到底在实际问题中是怎么运用的.
四、回顾活动过程,在经验的运用过程中通过抽象概括,形成思想方法.
在各小组纷纷做完练习并交流之后,老师提问:在刚才的运用过程中,大家有什么感受?
生11:这些公式用起来确实很好,但是九个公式有点多,容易弄混淆,而且什么时候用哪个公式好像也有点麻烦.
师:那么我们有没有什么办法让我们在用的过程中不那么容易混淆呢?
生12:我是通过画图来帮助我记忆运用这些公式的.
师:很好.当代数形式遇到困难时我们就用图形来帮助,这就叫数形结合.
生13:我好像看到了一个规律,无论哪一组公式,它们对应的三角函数名称都没发生变化,只是符号上有很多不一样的地方,好像有点麻烦,暂时还没找到规律.
这时所有同学的脸上都露出了笑容,似乎在说,真的是这样呢.
师:那我们能不能一起来努力看这些个不同的符号有什么样的规律呢,如果想不清楚,就可以回到我们探索这些公式的过程中去再想一想.
又是一番激烈的交流讨论.
生14:任何一个终边不在坐标轴上的角,其三角函数值都可以和一个锐角取得联系,它们对应的函数名称不变,符号就是这个角所在象限对应的三角函数值的符号.
看到其他同学都有些疑惑,老师作了一下沟通:你能不能具体地说一下是什么联系?
生14:当这个角是第一象限角时,它可以写成2kπ+α的形式,它的三角函数值就等于α的三角函数值;当这个角是第二象限角时,它可以写成(2k+1)π-α的形式,它的三角函数值在名称上和α的三角函数相同,但符号取决于第二象限角的对应三角函数值的符号,比如正弦为正,余弦和正切都为负;当这个角是第三象限角时,它可以写成(2k+1)π+α,它的三角函数值和α的三角函数相比名称上没变,符号取决于第三象限对应三角函数值的符号;当这个角是第四象限角时,这个角可以写成2kπ-α的形式,它的三角函数值和α的三角函数相比名称上没变,符号取决于第四象限对应三角函数值的符号.
众生都跟着点头,并露出了会心的笑意.
师:很好.这样具体问题具体分析,把枯燥的公式记忆连同其原理一起理解,形式上相得益彰,效果上事半功倍.可我却有一个问题,这里的这个α一定要是锐角吗?
同学们略微作了一下思考,都摇了摇头:应该不一定.但脸上都有些茫然:那该怎么说呢?这时老师写了一个问题:的三角函数值与的三角函数值之间有什么关系呢?
这时生3再次站了起来:只要一个角的终边与α角有一种对称关系,那么不管α角是不是锐角,这些式子都应该成立,这个α角都可以看成一个锐角,那么对应的三角函数值名称上与α的三角函数值名称上不变,符号取决于把α看成一个锐角时,2kπ+α、(2k+1)π+α、(2k+1)πα、2kπ-α所在象限角的三角函数值的符号.
沉默片刻,教室里爆发出一阵热烈的掌声.
师:让我们用掌声我们自己的努力和智慧喝彩!下面我们再回到教材第25页例2,大家看一看能不能用刚才我们归纳的公式来快速解决问题?
第二部分:课后反思
一、数学基本活动经验的形成需要操作过程,而概念课的教学,操作的重点在概念的形成、概念的理解和概念的运用上.具体到诱导公式来说,在探讨诱导公式的过程中,运用不同的操作方式让学生明白“诱从何来,导出什么”是重中之重,不然无论我们花多大力气,学生也不会明白为什么要学习这些公式,这些公式因何而来,为何而用.本节课在处理这个操作过程时借用了任意角的三角函数特别是三角函数线的概念中出现的四个图(参见人教版必修4第16页图1.2.7),发现任何一个象限角,它的三角函数都和一个锐角的三角函数有关这一已有经验进行探索,很好地让学生形成了利用诱导公式可以快速地确定一个角的三角函数值的应用经验.
二、数学基本活动经验的积累不可能一蹴而就,需要不断的积累.一方面,要充分发挥它在学习新知识方面的积极作用,另一方面还要在相同的、类似的数学活动中再次积累,直至形成深刻的、丰富的数学活动经验.本节课中,我们不断地从特殊角到一般角,从锐角到看成锐角,借助这些角的终边与这个锐角终边的特殊关系这一规律,再到只要两个角的终边具有这样的对称关系,我们都会得到这样的结构形式,从而得到一般化的公式及理解.
三、学生在概念的探索过程中,会自发地去运用一些已有的数学基本活动经验,也能够直接地获得一些懵懂、模糊的数学基本活动经验,我们有必要对学生所经历的数学活动通过回顾、反思等内在的思考,通过一些逻辑性的检验,实现感性经验向理性经验的转变,个人经验向学科的科学经验升级.本节课中,公式的探讨到什么程度为止,课前并没有预设,但随着学生探讨的不断深入,经验的不断积累,最终探讨到了在教材公式的基础上加上2kπ的形式,一定程度上有些意外之喜.
四、数学基本活动经验都会经历一个以积累为目的,到积累和运用相辅相成,再到纯熟的运用境界的过程.本节课中最终顺应了学生的实际,将公式扩展到在教材的基础上再加上2kπ的形式,一定程度上也是为后面再学习探讨三角函数图像性质特别是对称性服务.例如函数y=sinx的对称中心,学生根据周期性很容易接受可以是(2kπ,0),但为什么(2kπ+π,0)也是其对称中心就很不容易弄明白.如果学生能够运用到本节课中公式的探索中所积累的数学基本活动经验,那么在理解上就会顺畅得多,自然得多.
五、在数学基本活动经验下的教学对教师的教学也是一种挑战.尊重学生数学基本活动经验的积累与运用就意味着我们要对学生可能具有可能运用到的数学基本活动经验有一个预判,也意味着课堂上将会有更多我们没有设想到的场景和问题,也意味着我们的教学目标不能再那么固定和僵化,而要根据课堂上可能出现的问题进行不断调整,更意味着我们今天所积累的数学基本活动经验是为了今后的运用而要求我们的教学要有更好的前瞻性……所有这些问题,都将是摆在我们面前所要面对的挑战.
