让学生的思维在课堂中自然流淌——以高三一轮复习“圆锥曲线中的转化问题”教学为例
2016-04-05浙江省镇海中学朱寒杰江苏省天一中学何志奇
■浙江省镇海中学 朱寒杰■江苏省天一中学 何志奇
让学生的思维在课堂中自然流淌——以高三一轮复习“圆锥曲线中的转化问题”教学为例
■浙江省镇海中学朱寒杰
■江苏省天一中学何志奇
2015年12月11日,江苏省海门中学举办了第31届教学“百花奖”全国展示活动.作为邀请嘉宾,笔者很荣幸站在海门中学的讲台上展示了一节高三圆锥曲线的复习课,课后,受到了江苏省天一中学数学特级教师、教授级高级教师——何志奇教授和其他与会教师的一致好评.现将本节课的教学设计、自己的点滴感悟和何教授的专家点评分享如下,供同行参考.
一、教学设计
笔者拿到的课题是高三一轮复习——直线与圆锥曲线的位置关系,翻阅苏教版选修2-1教材和2015年江苏高考数学考试说明,均未找到这一知识点.于是笔者准备将本课的题目定为“圆锥曲线中的转化问题”,任何圆锥曲线解答题只有进行了合理的转化才能有准确的计算.故探讨这一问题,显得很有意义.
1.五年高考切入课题
本课以江苏省2011~2015年五年高考的圆锥曲线大题为切入点,分析各题中的关键条件的转化,从而让学生感受到条件转化在圆锥曲线问题中的重要性.从学生最感兴趣的高考题入手,快速吸引学生的注意力,提升本节课的学习兴趣.
2.典型例题展开课题
在学生求知欲最强的时候,立即给出如下例题:

图1
本题设计思路清晰,题目简洁明了,解题策略丰富多样,能够充分体现“圆锥曲线中的转化问题”这一主题.根据学生对条件的不同转化方式,本题给出如下三种解题策略.
策略1:

解答:设MN方程为x=my+1,代入8x2+9y2-72=0,消去x,得(8m2+9)y2+16my-64=0,
策略2:

解答:设AM方程为x=ty-3(t≠0),代入8x2+9y2-72= 0,得(8t2+9)y2-48ty=0,
又右焦点坐标F2(1,0),所以MN方程为代入8x2+9y2-72=0,
由MA⊥NF1,故kAM·kNF1=-1,即
策略3:

又因为MA⊥NF1,所以直线NF1方程为
化简得16t4-33t2-45=0,即(t2-3)(16t2+15)=0,
从课堂的教学情况来看,课前预设的这三种策略正是学生上课时依次想到的.这也让学生的思维在课堂中自然地流淌.
通过这道例题的讲解,告诉学生:“圆锥曲线问题一旦转化不得力,就会遇到计算的麻烦.所以,大家在遇到计算中的困难时,除了暴力求解,也请多思考最优的解法.毕竟只有改革创新,社会才能进步!”
3.经典练习深化课题
正当学生的思维处在最兴奋的时候,给出如下练习,让学生体会在计算过程中转化问题.

图2
本题可以视为例1的变式,学生在解答过程中可以利用例1解答中的部分过程.本题给出如下四种解题策略.
策略1:利用求根公式,代入化简,得

策略2:利用“消元”思想,代入化简,得

策略4:寻找出现问题的“根源”:
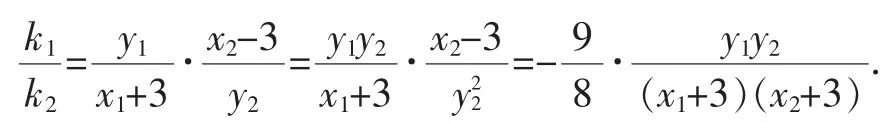
4.探究发现拓展课题
高中数学学习不应仅仅学习知识,还应主动提出问题,发现问题,培养自身的探究能力,于是本教学环节引导学生从特殊到一般的角度对练习题进行拓展延伸.“从特殊到一般”和“从一般到特殊”,是认识问题的普遍规律,按照梅森的观点,特殊化与一般化正是数学思维的核心,同时也是怎样解题的关键所在.
人教版选修2-1第77页中的“阅读材料”给出了圆锥曲线在直角坐标系中的统一方程.于是,结合学生的讨论,我顺势给出如下命题,供学生课后思考.
在平面直角坐标系xOy中,已知曲线C:(1-e2)x2+y2-2pe2x-p2e2=0,A,B为曲线C与x轴的两个交点,过定点D(n,0)的直线l与曲线C交于M,N两点.设直线AM,BN的斜率分别为k1,k2.求证:为定值.
二、点滴感悟
1.圆锥曲线复习什么
圆锥曲线是全国各地高考的重点考查对象.历年各地高考题中均会出现圆锥曲线解答题,此题往往会成为各位考生的噩梦.那么圆锥曲线试题的难到底难在哪里呢?笔者认为,就是转化和运算.转化是指“合理拆分圆锥曲线的几何特征与代数表示”;运算是指“分析运算条件、探究运算方向、确定运算程序、检验运算结果”.所以我们在复习中要从这两方面帮助学生克服心理障碍.这也正是我们在圆锥曲线复习中要着重强调的两个方面.在分析每一道圆锥曲线试题时,都要从这两个方面帮助学生突破难点.
2.圆锥曲线复习课怎么上
经过这次展示活动,笔者认为要备好一节圆锥曲线复习课,需从以下四个方面重点突破:(1)精选例题.要在一节45分钟的课堂上教给学生更多的知识,一道简洁明了的例题是必不可少的,不在题意上给学生设置障碍.同时,此题还必须具有“开放性”,学生无论用“通性通法”还是“独门绝技”都能解决的例题才是好的例题. (2)变式训练.笔者认为,例题是教师在课堂上通过自己的讲解,帮助学生达到预设的教学目标.而练习则是教师希望学生通过自己的努力巩固刚刚学到的知识与方法.所以要达到一节课的教学目标,除了例题的讲解还必须配有相应的练习.而此练习要尽可能地对例题进行变式拓展,这样就能充分利用例题中的解答过程,最大程度地利用45分钟的宝贵时间.(3)留有思考的空间.一节完整的课并不意味着要解决所有问题,笔者认为要将课堂内容适当地延伸到课堂外,给学生留有思考的空间,使得学生上完本节课仍然意犹未尽.(4)留有总结的时间.海门中学的做法是:在一节课结束前3分钟会有一个铃声,用来提醒上课教师一节课的总结时间到了.笔者认为这是一个很好的做法.很多时候,不在于你教给学生多少,而是学生自己总结了多少.不仅如此,笔者认为还应将总结的时间交给学生,让学生自己谈谈一节课的收获.
三、专家点评
点评专家:何志奇(江苏省特级教师、江苏省首批教授级高级教师)
(1)能紧扣教学重点与学生在解析几何中最容易出现的困难进行分析.解析几何的本质是几何问题代数化,而本课的教学目标是学会对解析几何问题进行合理转化,目标定位准确具体、全面且适当.其中当学生的思路与教师的思路发生偏差时,朱老师能顺应学生的思路,给学生恰当的指导来帮助学生获取成功,而不是强行将学生的思维纳入教师思维的轨道,课堂上学生没有感到很失败,没有沉默不语,教师也没有一个人在唱独角戏,学生尝到的是解法成功的喜悦.从学生的角度来看,例1的策略1和策略2,学生是很自然想到而获得成功的.
(2)本课一大亮点是抓住一道题进行展示.就像拍照,同一个人以不同的姿势拍出各式各样的照片.圆锥曲线复习不在于题目的多少,而在于对同一道题能否从某个方法上或者某个知识点角度进行深入的挖掘.本节课对例1进行了非常深入的挖掘,将题目的演绎发挥得淋漓尽致.高三复习,一节课需要多少题目?贵在精,不在于灌.朱老师用一道题目一个课堂练习围绕解析几何的“转化”核心演绎了精湛的教学艺术.
(3)在课堂演绎过程中,以最快的速度切入主题,迅速吸引学生的眼球.这在圆锥曲线复习课中非常重要,为后续腾出更多的时间进行题目的剖析与演绎.本课的教学完全顺着学生之意进行展示,尊重学生的个体思维差异,学生回答什么,就讲什么方法,并未刻意地向学生灌输相关知识与方法.真正做到老师的一桶水,准备充分,为不同层次的学生在数学知识与数学技能等方面提出不同思维层次的要求.
(4)本课的另一亮点则是将解题过程写成框架图,显得非常清晰,逻辑意识润物细无声地渗透到学生的心里,学生印象深刻.
(5)本课的一大遗憾则是未让学生提出问题,哪怕是一个问题也好的呀!李政道先生曾说过:“求学问,需学问;只学答,非学问.”我们现在的学生“只会答,不会问”.在实际的教学中,我们应该把更多的时间留给学生,让其能够“于无疑处有疑”.
感谢江苏省海门中学给了笔者这样一次展示教学的机会.从备课、磨课到上课,笔者收获良多,尤其是何教授的精彩点评,笔者一定会谨记于心.在今后的课堂教学中,努力做到把“更多的时间留给学生”,让其能够“于无疑处有疑”.
参考文献:
1.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
