基于PDE的错位ESPI无损检测方法与系统实现

张　芳，孙　娇，马　潇，檀玉飞，王晋疆

（1.天津工业大学电子与信息工程学院，天津300387；2.天津大学光电信息技术教育部重点实验室，天津300072）



基于PDE的错位ESPI无损检测方法与系统实现

张芳1，孙娇1，马潇1，檀玉飞1，王晋疆2

（1.天津工业大学电子与信息工程学院，天津300387；2.天津大学光电信息技术教育部重点实验室，天津300072）

摘要：设计并实现了电子散斑干涉无损检测系统，搭建了错位电子散斑干涉光路.采用基于偏微分方程的电子散斑干涉信息提取技术对采集到的散斑图像进行处理，结合条纹图自身的方向信息，利用偏微分方程提取电子散斑干涉条纹图的中心线并进行相位插值，得到物体的变形信息，从而实现无损检测.实验结果表明：本文方法提取的相位平均误差在2%以内.

关键词：无损检测；错位电子散斑干涉；偏微分方程；相位提取

（PDE）；phase extraction

无损检测是工业发展的重要技术，在一定程度上反映了一个国家的工业发展水平，常用的无损检测技术有超声检测[1]、射线检测、红外检测、光学检测等.超声波技术和射线技术检测速度较慢，不适合做全场检测；缺陷深度对红外检测的温度场的最大温差和延迟时间都有影响，很难对测物的缺陷深度信息进行测量.光学干涉测量技术测量精度高，能够测量微米级上的物体表面的微小变形，其检测结果可为生产技术环节的改进提供精准的反馈参考，使进一步提高生产方面的技术成为可能.电子散斑干涉测量技术（electronic speckle pattern interferometry，ESPI）是一种重要的无损检测技术，它利用光学干涉的方式记录待测物体变形前和变形后的散斑干涉场，通过比较2幅散斑场的差异获得反映物体形变量的一幅干涉条纹图[2].由于干涉条纹是干涉场中光程差相同点的轨迹，因而可以根据干涉条纹的方向、形状和疏密，获得与光程差有关的被测量信息.通常采取的做法是利用图像处理技术从条纹图中提取出干涉条纹的相位，进而根据条纹相位和被测物理量的关系获得物体的微小位移、形变信息或进行缺陷检测[3-6].错位电子散斑干涉技术抗震性好，对物体的变形非常敏感，可以直接测量物体的应变.

基于偏微分方程（partial diffusion equation，PDE）的图像处理模拟物理上的热扩散过程，将图像的灰度值看作热量，将图像处理过程看作热量的扩散过程，通过设置一定的扩散方式调整热量分布，使图像灰度值进行重新分配和排布，最终实现图像滤波、对比度增强、图像分割等.目前利用偏微分方程提取电子散斑干涉测量信息主要集中在滤波和提取中心线. Tang 等[7]和Wang等[8]分别提出了方向偏微分方程滤波模型和一致增强偏微分方程，按照条纹走向调整滤波方向，大大改善了偏微分方程对干涉条纹图的滤波效果. Tang等[9]提出一种基于梯度矢量流场的中心线提取算法，利用偏微分方程实现对光干涉图像中心线的自动提取，保留了原始图像的重要信息，也保证了中心线提取的精确性.

本文改进了Tang的中心线提取方法，并且提出利用偏微分方程进行相位插值，有效提取ESPI条纹的相位信息.

1　错位电子散斑干涉测量技术

在力学中，往往需要的是应变，即位移的导数.错位散斑干涉法可以直接得到位移的导数，而且防振性能好.错位散斑测量光路如图1所示.图1（a）为错位散斑图的记录光路图，它最大的特点就是在光路中布置了一个错位装置，其作用是使得被测物表面的P1和P2两点在像平面上重叠在一起，认为是P点，δx是错位量，图1（b）为变形量与位移的关系示意图.

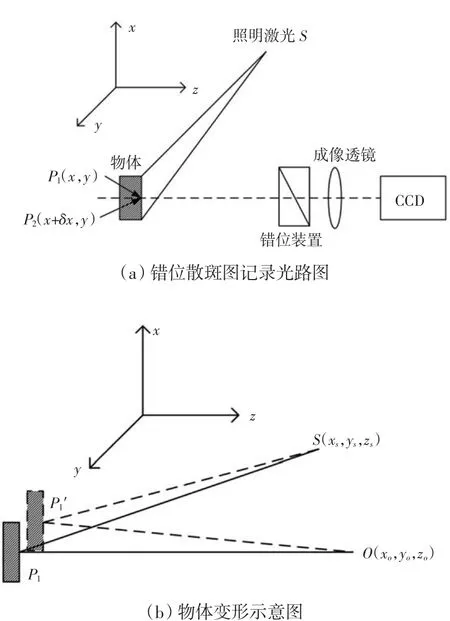
图1　错位散斑测量光路图Fig.1 Shearing speckle measuring light path map

在图1（a）中，被测物表面P1和P2两点在像平面上重合.设由P1点反射的光在像面上的波前和P2点反射的光在像面上形成的波前分别为：

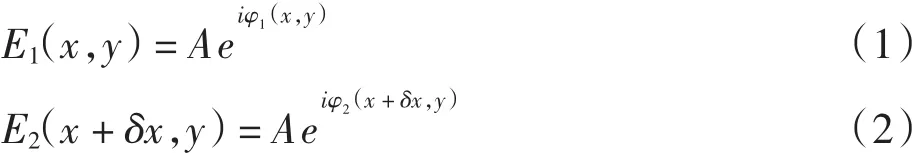
式中：假设两点振幅A是相等的，仅相位不同，分别是ψ1（x，y）和ψ2（x +δx，y）.物体变形前，两束光波的合成复振幅为

对应的光强分布为

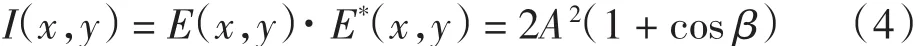
式中：β为两相位的差值，即β=ψ2-ψ1.

当物体变形以后，点P1移到P1′，P2移动到P2′，相应的ψ（1x，y）和ψ（2x +δx，y）变成了ψ（1x，y）+δψ（1x，y）和ψ（2x +δx，y）+δψ（2x +δx，y），这时两束光波的合成光强为

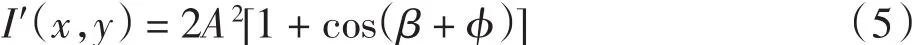
式中：φ=δψ2（x +δx，y）-δψ1（x，y），它是由两点间光程改变而引起的两波面间相应的相位差.

本文采用相减模式获得散斑干涉条纹图像，它是相位φ的正弦调制图像，相应表达式为：

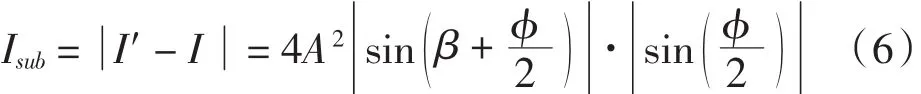
式中：sin(β+φ/2)中包含随机的高频项β，在图像中表现为噪声；sin(φ/2)是有规律的，它与物体的形变有关[10].当φ= 2nπ，n = 0，±1，±2，…时，I（x，y）= 0，呈现暗条纹.

当仅沿x方向错位并调整照明方向和观察方向基本一致时，由两点间的变形而引起的相位差，由两点间的变形而引起的相位x与错位量δx的关系是：

在得到干涉条纹图后，一般需要对条纹图进行滤波[11]、二值化、提取条纹中心线、级数指派、相位插值等一系列操作，从而获得相位φ（如果仅沿x方向错位，

则这里φ=φx），进而提取物体的位移导数

及形变信息[12].本文采用偏微分方程中心线提取方法，可跳过滤波和二值化的处理过程，直接对含有噪声的条纹图Isub处理得到条纹中心线.

2　基于偏微分方程的条纹相位提取

本文采用基于偏微分方程的图像处理方法提取条纹信息，其主要处理步骤如图2所示.

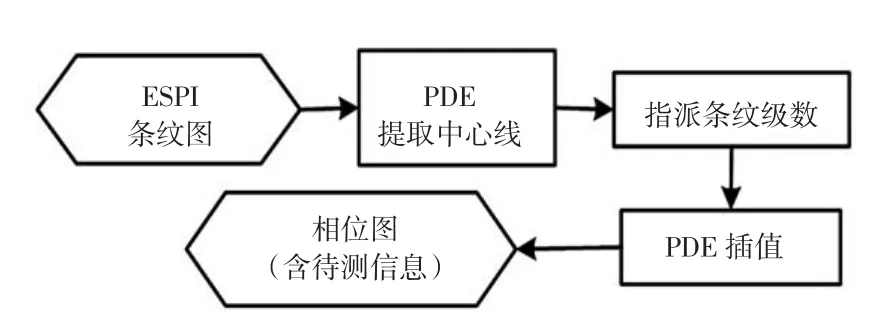
图2　ESPI条纹信息提取过程Fig.2 Process of ESPI fringe information extraction

2.1基于PDE提取条纹的中心线

本文利用偏微分方程结合梯度场的散度特性来提取条纹图的中心线.首先计算原始ESPI图像的梯度矢量场，I（x，y）表示ESPI条纹图像素点（x，y）处的灰度值，初始梯度矢量场可表示为：

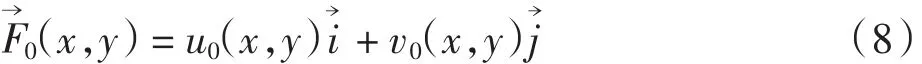
式中：u0、v0分别为图像I（x，y）的梯度矢量场在、上的2个分量，表示为：

由于散斑噪声对梯度矢量场有影响，因此本文利用偏微分方程来调整u0场和v0场，去掉噪声.本文采取的各向异性扩散偏微分方程可以表示为：

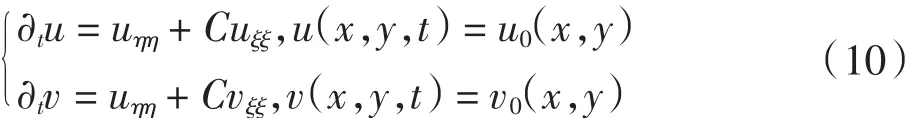
式中：C为常数；uηη和uξξ分别为u沿着孜方向和浊方向的二阶导数；为了计算内在坐标系中uηη、uξξ、vηη、vξξ，引入条纹图的方向角θ，它表示条纹方向与x轴之间的夹角.那么uηη和uξξ可用下面的公式计算：

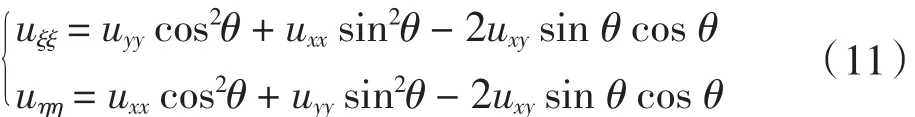
vηη和vξξ同理可得.

求解方程（10），得到调整后的梯度分类，从而获得新的梯度矢量场：

该方法利用图像处理中的梯度信息和方向信息使得处理结果更精确，根据调整后的梯度矢量场（u，v），计算F軋的散度，判断黑条纹和白条纹所对应的源点和汇点.

根据散度的分析，如果A < 0，像素点（x，y）属于白条纹中心线上的点；如果A > 0，像素点（x，y）属于黑条纹中心线上的点.为了获得单像素宽度的中心线并且减少运行时间，在散度分析后需进行有限次迭代和形态学细化操作.

2.2条纹中心线级数指派

提取出来的中心线上的点像素值为0、1，这些值显然不是实际的相位值.为了求得实际的相位值，首先采用人机交互的方法对中心线进行级数指派.先设定某一条纹级数n，相邻条纹的级数为n±1，其中向峰顶方向为+1，向峰谷方向为-1.由于相减模式得到的条纹图中明条纹与暗条纹中心线间的相位差为π，因此将设定好的条纹级数乘以π，便得到中心线上的相位值.

2.3基于PDE进行相位插值

经过级数指派并对条纹级数乘以π后，中心线上的点已经具有了真实的相位值.而对于非中心线上的像素点，其相位值需要同过插值技术获得.本文提出基于热传导方程的相位插值方法，在指派中心线级数的基础上利用热扩散原理[13-14]获得全场相位.热传导方程如式（14）：式中：IP（x，y）为待插值的图像，经过式（14）的扩散调整后，得到插值后的结果u.

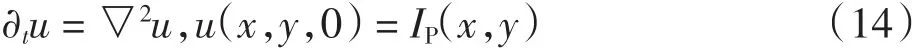
以级数指派后的图像IP（x，y）作为初始图像，将图像中的灰度值看作是平面物体的温度分布，利用热传导原理，经过热量扩散后得到全场的相位图像.经级数指派后的条纹图仅中心线上有灰度值，根据热传导原理，中心线上点的确定温度值为平面物体提供了热量，引起中心线外点的温度变化，经过一段时间的热交换，中心线以外点的灰度值接近邻近中心线上点的灰度值，从而实现相位插值的目的.在这一过程中，中心线上点的确定温度值是插值图像变化的动力，因此在该模型的实现过程中，必须反复利用中心线上点的确定温度，进行多次迭代才能达到预期目的，使得获取的全场相位逼近真实相位.

图像上各点的插值均与近邻点的像素有关，边界的不φ确势必会影响某些点插值的准确性，因此需要对边界条件进行限定，即每次迭代前使得最外层的相位值等于次外层的相位值，最大限度的减少了边界对插值准确度造成的影响.

3　错位电子散斑干涉检测系统设计

本文设计的错位电子散斑干涉无损检测系统包括光源照明系统、错位装置、加载装置和图像处理装置，如图3所示.

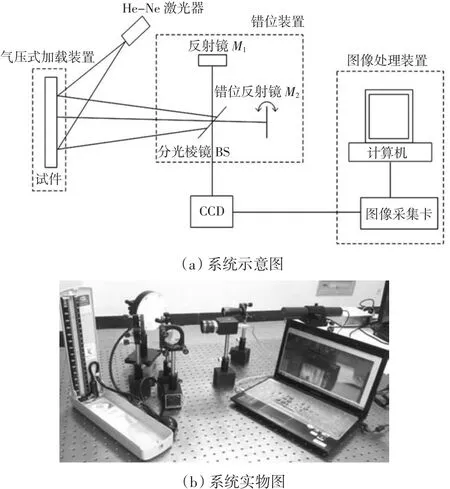
图3　搭建的无损检测系统Fig 3 Nondestructive system

本文设计并实现了可视化界面，图4为错位电子散斑干涉测量系统的操作界面，该系统可实现对初始条纹图进行条纹中心线提取和相位插值，最终获得全场相位.

图4　错位电子散斑干涉检测系统操作界面Fig.4 Interface of shearing speckle measuring system

4　实验测试与结果

利用本文搭建的无损检测系统，对四周固支、中心加载的圆盘进行无损检测，结果如图5所示.

图5　对圆盘变形的实验结果Fig.5 Experimental results of deformed disc

为了说明本文方法的性能，将本文的方法与传统的样条插值方法进行对比.本文采用的力学模型为受均布法相载荷的周边固支的圆板，可以模拟复合材料中真空加载条件下的变形、分层、脱粘缺陷.实验装置的具体参数为：激光光源为He-Ne激光，姿= 632.8 nm；工作距离为400 mm；光源位置为（0，0，400 mm）；视场范围为120 mm×120 mm；加载变形位置为视场中心；变形面元直径为20 mm；变形面元最大离面位移为2 μm.

图6为模拟圆板变形测量的实验比较结果.由图6可见，传统的样条插值方法得到的相位图并不平滑，边缘处毛刺很多，与真实相位值偏差比较大；而本文的方法得到的相位图比较平滑，提取的相位值更接近真实相位值，将本文方法得到的相位值与真实的相位值进行误差分析，平均误差在2%以内.

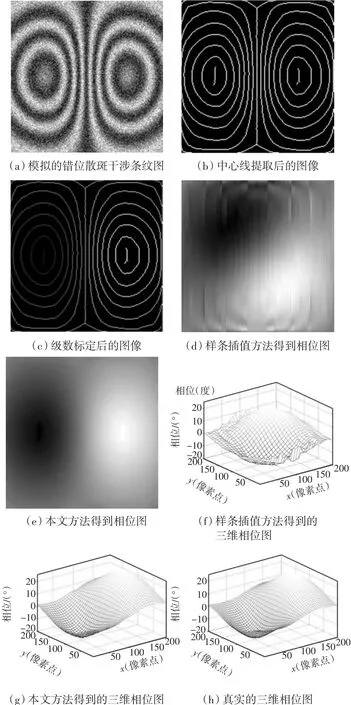
图6　模拟圆板变形测量的实验比较结果Fig.6 Experimental comparison results of simulated deformation of circular plate

5　结语

本文设计并实现了错位电子散斑干涉测量系统，利用错位电子散斑干涉测量系统获取物体的干涉条纹图，然后利用基于偏微分方程的电子散斑干涉信息提取技术对条纹图进行处理来实现无损检测.本文方法跳过了传统条纹图处理过程中的滤波和二值化的过程，直接得到条纹的中心线进而插值得到全场相位，提高了相位提取的精度.对圆盘进行变形检测及定量分析，定量分析结果表明，本文方法提取的相位平均误差在2%以内.而本文组建的错位电子散斑干涉测量系统只适用于实验室条件下的测量，如何实现测量系统的光路集成化以适应工业现场及复杂测量环境的需求有待进一步的研究.

参考文献：

[1]王以民，苗长云，白华.大型锻件多路超声检测系统的研制[J].天津工业大学学报，2014，33（2）：48-52. WANG Y M，MIAO C Y，BAI H. Development of multi -channel ultrasonic testing system on heavy forging[J]. Journal of Jianjin Polytechnic University，2014，33（2）：48-52（in Chinese）.

[2]王海涛，万敏，姜兆芳，等.电子散斑干涉技术的发展及其在无损检测方面的应用[J].南昌航空大学学报，2007，21 （S）：75-79. WANG H T，WAN M，JIANG Z F，et al. The development and application of ESPI technology on nondestructive testing [J]. Journal of Nanchang Hangkong University，2007，21（S）：75-79（in Chinese）.

[3]李飞，张鲁殷，胡晓军，等.基于一维电子散斑干涉仪对复合材料的无损检测[J].大学物理实验，2015，28（1）：19-21. LI F，ZHANG L Y，HU X J，et al. Nondestructive testing of composite materials based on out-of-plane electronic speckle pattern interferometery[J]. Physical Experiment of College，2015，28（1）：19-21（in Chinese）.

[4]李斌，杨国标.电子散斑干涉在复合树脂固化收缩测试中的应用[J].同济大学学报，2012，40（1）：133-136. LI B，YANG G B. Electronic speckle pattern interferometry method applied to measurement of shrinkage deformation of light-cured composite resin [J]. Journal of Tongji University，2012，40（1）：133-136（in Chinese）.

[5]张羽鹏，王开福. LabVIEW和MATLAB在电子散斑干涉图像处理中的应用[J].激光技术，2009，33（6）：582-585. ZHANG Y P，WANG K F. Application of LabVIEW and MATLAB in ESPI image processing[J]. Laser Technology，2009，33 （6）：582-585（in Chinese）.

[6] QIN Y，CHEN J，FAN H. The study and application of a new filtering method on electronic speckle pattern interferometric fringe [J]. Optics and Lasers in Engineering，2003，39：449-456.

[7] TANG C，HAN L，REN H，et al. Second-order oriented partial-differential equations for denoising in electronic-specklepattern interferometry fringes [J]. Optics Letters，2008，33 （19）：2179-2181.

[8] WANG H，KEMAO Q，GAO W，et al. Fringe pattern denois－ing using coherence-enhancing diffusion [J]. Optics Letters，2009，34（8）：1141-1143.

[9] TANG C，LU W，CAI Y，et al. Nearly preprocessing-free method for skeletonization of gray-scale electronic speckle pattern interferometry fringe patterns via partial differential equations[J]. Optics Letters，2008，33（2）：183-185.

[10] YU J. A system of image processing based on ESPI[J]. Information Technology，2003，27（4）：41-43.

[11]韩艳娇，陶纯匡.基于MATLAB的数字散斑条纹图滤波比较[J].电子世界，2013（8）：169-170. HAN Y J，TAO C K. The Compassion of filters for digital speckle fringe pattern based on MATLAB [J]. Digital World，2013（8）：169-170（in Chinese）.

[12] ZHU W，JIAO K，XU C. Extraction of laser stripe center line based on genetic algorithm and NURBS interpolation [J]. Journal of Beijing Institute of Technology，2008，17（2）：143-147. [13]王朔中，克达尔，秦川，等.应用热传导模型的偏微分方程图像修复[J].上海大学学报，2007，13（4）：331-336. WANG S Z，KE D E，QIN C，et al. PDE-based image inpainting using a heat transfer model[J]. Journal of Shanghai U－niversity，2007，13（4）：331-336（in Chinese）.

[14]巩文迪.基于偏微分方程的图像去噪算法研究[D].邯郸：河北工程大学，2013. GONG W D. Study on algorithm of image denoising based on partial differential equation[D]. Handan：Hebei University of Enginering，2013（in Chinese）.

Shearing ESPI nondestructive testing method based on PDE and system implementation

ZHANG Fang1，SUN Jiao1，MA Xiao1，TAN Yu-fei1，WANG Jin-jiang2
（1. School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China；2. Key Laboratory of Opto-Electronic Information Technology，Ministry of Education，Tianjin University，Tianjin 300072，China）

Abstract：A shearing electronic speckle pattern interferometry light path is built，and a nondestructive testing system of electronic speckle pattern interferometry is designed and implemented. The partial differential equation image processing technology is used in speckle image processing. Combined with the direction of fringes，the partial differential equations are applied to skeleton extraction and phase interpolation to obtain the deformation information of the object. The average error of the extracted phase from the proposed method is less than 2%.

Key words：nondestructive test；shearing electronic speckle pattern interferometry（ESPI）；partial differential equation

通信作者：张芳（1981—），女，博士，副教授，硕士生导师，主要研究方向为图像处理与模式识别，光学干涉无损检测. E-mail：hhzhangfang@126.com

基金项目：国家自然科学基金资助项目（61102150）；电光信息技术教育部重点实验室（天津大学）开放基金（2013KFKT011）；天津工业大学大学生创新创业训练计划项目（201410058）

收稿日期：2015-09-01

DOI：10.3969/j.issn.1671-024x.2016.01.008

中图分类号：TG115.28；TP391

文献标志码：A

文章编号：1671－024X（2016）01－0038－05