学生数学学习错误的转化策略
2016-04-02章刘飞
章刘飞
在数学学习过程中,小学生出现错误的原因,其一是习惯性错误(指会做而做错),其二是知识性错误(不会做而做错)。教师应“因错纠错”,紧紧抓住“合适”的错误契机,利用学生的错误资源,让学生经历一次次错误的探险,从而感受到心理的挫折、惊喜与顿悟,并从中获得质疑、反思和多向思维的创新价值。
一、多样表征重点错例,重新建构概念
重点错例,即学生对于重点概念理解有所偏差的错误。运用多样表征就是让学生能够更好地阐述自己的想法,让他们各抒己见,从而使学生在学习中既长知识,又提高学习能力。
《平行四边形面积计算》教学片断。
教师出示一个长方形,让学生计算面积,毫无悬念地得出答案之后,教师又出示一个边长分别是6厘米和4厘米的平行四边形,让学生猜想它的面积。经过一番激烈的讨论,学生们得出两种不同的猜想:
猜想一:参照了长方形的面积计算方法,认为这个平行四边形的面积是相邻两条边的乘积,也就是6×4=24(平方厘米);
猜想二:画出了平行四边形底边上的高,经过测量,得出高是3厘米,面积是底乘高,也就是6×3=18(平方厘米)。
(学生讨论,教师引导)
生:平行四边形容易变形,如果把它变成长方形,长方形的面积是长乘宽,平行四边形的面积就是边长乘边长。
生:如果把这个平行四边形压得很扁很扁,底的长度是不变的,面积还是24平方厘米吗?
教师黑板演示
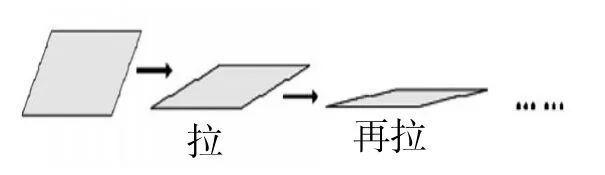
师:在平行四边形变形的过程中,你看到了什么在变,什么没有变?
生:面积在变,边长没有变。
学生的认知过程并不是一条平缓延伸、波澜不惊的直线,而是一个不断犯错、不断修正的过程。所以说,关键不在于错误,而在于我们怎样纠正错误。首先,教师要注意倾听学生的奇思妙想。其次,教师要将错就错地引导和化解,当学生出现错误,不要急于纠正,而要给学生充分的时间去发表意见,去说明观点,再予以剖析,其效果自然是事半功倍。
二、多次验证疑难概念,深化理解概念
有些概念是教学的难点,一时之间学生确实难以接受,这就需要教师不断引导学生去探索、试验、证明,从而使其在实践中更好地得以理解掌握。
《圆锥的体积》教学片断。
师:下面分组做实验,在空圆锥里装满沙子,然后倒入空圆柱中,看看几次正好装满。
师:请同学们利用手中的圆柱和圆锥、沙子,从倒的次数看,研究两者的体积之间有怎样的关系?
生:我们将空圆锥里装满沙子,然后倒入空圆柱中,三次正好装满。说明圆锥的体积是圆柱的三分之一。
师:有没有不是这样的?
没有!没有!学生齐声回答。有学生还说书上也是这样写的。
老师故意惊讶:怎么会这样呢?全都是三分之一?我也来做。(教师从教具箱中随手取出一个空圆锥一个空圆柱),你们看,将空圆锥里装满沙子,倒入空圆柱里,一次,再来一次,两次正好装满,圆锥的体积是圆柱的二分之一,怎么回事?是不是你们做的和书上的结论都有错误?学生开始有议论……
师:你们说说该怎么办?究竟是谁对呢?
生:老师,你取的圆锥太大了。
师:我不也是一个圆柱,一个圆锥吗?
于是学生个个争先恐后想提出自己的看法和意见,圆柱的体积和圆锥的体积的关系也就理解和掌握得更加深刻了。
学生通过动手操作得出的结论与书上的结论没有差异,并不能说明学生真正掌握了知识,这时候教师在教学中有意创造错误,使学生产生思维碰撞,让学生经历一番热烈争辩,然后得出“圆锥体积等于等底等高的圆柱体积的三分之一”这个结论。这样让学生在看似混乱无序的实践中,增强其对实验条件的辨别能力及错误信息的批判能力。既圆满地推导出圆锥的体积公式,又促进学生的实践能力和批判意识的发展。
三、“三多”互动,合理引导,培养良好的计算习惯
1援多途监控基本题。
多途监控即采取多种途径对学生的计算方法进行展示、筛选和优化。所以说,计算之前仔细观察和思考,找出最便利的方法,这也是学生需要培养的计算习惯之一。
如:当学生学了小数的乘法时,经常要做一些“找朋友”的练习题:
3.5×1396.6
4.6×2145.5
2.3×1739.1
有一类学生看到题后,马上拿笔就算,另一类学生并不马上动笔,而是认真看题,想题中算式与结果的关系。
结果,第二类学生不但结果正确,而且比第一类学生速度还快。因为后者通过认真读题,发现每个结果的末位的数不相同,用两个因数的最末位数字的数相乘就能找到正确的答案。这样,不但节省了时间,同时他们在理解的过程中,理解问题的能力也得到了提高。
同样一道题目,通过仔细观察,利用自己所掌握的知识,能探究出一些解题的巧法,这样,不仅节约了学生的解题时间,更关键的是提高了正确率,同时学生也体会到了学习的快乐、灵活解题的乐趣,达到了事半功倍的效果。
2.多边自控简算题。
“书读百遍,其义自见”,学生在解决问题前必须首先“熟读”、“感悟”问题,这是一个由“粗读——再读——细读”产生“寻疑——释疑——解析”的过程。因此,教师在教学过程中要培养学生看题、读题、想题的良好学习习惯。
如:在《小数的简便计算中》,设计了两组比较题:
第一组:
①2.5×(4×0.4)
②2.5×(4+0.4)
第二组:
①3.6×10.1
②3.6×0.99
设计第一组比较题的目的是为了清楚地比较出乘法结合律和乘法分配律的不同。在实际的课堂中我们发现,还有三分之一左右的学生对这样的题目很容易混淆,当然这其中也有一部分学生是审题不够仔细,但通过这样的对比练习,很清楚地让学生知道他们的区别,犯错几率自然大大减少。
设计第二组比较题的目的是为了强化乘法分配律的实际应用。在以往的考试中,我们往往能够发现乘法分配律是必考的,而这一组题目是对乘法分配律的灵活运用的比较,因为一般的乘法分配律往往出现的是一个数乘两个数的和或差,或者是乘法分配律的逆运算,而这两道题需要先拆分再运用乘法分配律,所以在难度上有一定的提高。
3.多向调控综合题。
灵活应用所学的知识,这是一个很好的学习习惯。学习的目的在于应用,将课堂上学到的知识加以灵活运用,既能起到巩固和消化知识的作用,又有利于将知识转化成能力,还能实现培养学生学习数学兴趣的目的。
如计算:
第一组:
①6.8×25-28×2.5
②1.9+1.9+1.9+1.9+1.7
第二组:
如图,在一个正方形花坛的外面围着一条宽2.5米的小路,小路的面积一共是150平方米,那么这个正方形花坛的边长是多少米?

第一组题的目的是拓宽解题思路,要求用多种方法解题,同时优化最佳方法,如第①题建议优化用乘法分配律解决,第②题建议优化看成整数计算比较简便。
第二组题的解法比较多,既可以用算式方法也可以用方程来解决,但如果是突出简便计算的核心的话,建议学生用算式方法解决,如用“150÷4÷ 2.5-2.5”的方法比较简便。
