代数思维的启蒙———二年级图形推理课教学设计

王国宏

本节课根据新思维数学相关内容设计，既为进一步巩固和应用除法的知识，也是推理能力的专项训练，为今后推算图形等式、方程等做铺垫。教学时，要充分保证学生观察和思考的时间，重视学生思考的过程。要注意引导学生分析解题思路，寻找解决问题的切入口，从一元到二元，抓住两个等式之间的联系，初步感知消元法、代入法的运用。

我们力求从学生的学习基础、学习过程、学习方法出发，通过数形结合、图形推算、抽象建模、回顾过程等方法来突破难点、落实重点、实现拓展。

一、数形结合突破难点——从学习的基础角度出发

【设计预期】对于二年级的学生来讲，本课的等量代换思想，以及所要启蒙的代数思维都是比较抽象的，这也正是本课教学的难点。为此在教学设计的过程中，教师需要给学生一些具体的、生动的、可见的图形去帮助学生理解，否则学生就会显得无从入手。为此教师利用数形结合的思想，在激发学生兴趣的同时，让学生能初步感知“换”的思想，以求实现事半功倍的效果。

【教学实施】手势游戏

①☆+3=8☆=（ ）

②☆+☆+☆=9☆=（ ）

③☆+○=6○=3☆=（ ）

④☆+○=20

○=（ ）☆=（ ）

师：你能用手势告诉大家它们的答案吗？请说一说你是怎么想的？

师：这一题（第④小题）为什么大家的得数不一样了呀？你能知道它们的答案有可能是几吗？写一写。

师：出示下图，现在能确定了吗？

☆+○=20

☆=○+○+○

师：你又能找到多少种答案，试着做一做。

（引导学生说出自己的解题思路，并从中得出一个基本的方法“换”）

出示：

誙+△=45

△=誙+誙+誙+誙

师：现在还能继续换吗？

小结：类似于这样的一组题目我们都可以通过“换”的方法来找到答案。

【实践成效：基础训练的前三题实现了学生的热身环节，使得全体学生都能从低起点投入本课的学习。特别是第4小题，开放性的设计，让学生体会到一个等式中未知数的个数大于1个的时候会有很多的可能性，通过确定一个或几个未知数，从而使等式中的其他未知数也确定下来，答案就能唯一。这一题看似简答，实际是设计者精心的安排，同时也为下一步的教学衔接铺垫。接着通过补充条件，让学生感知本题的开放性，并充分体会到通过“换”能抵消掉两个未知数中的一个，才能使等式变成只含有一个未知数的等式，转化为学生能解决的问题。

这样的导入不仅起点低，而且让学生有了对于本课知识的铺垫，通过数形结合的思想，让学生能一目了然的领悟“换”的思想，解决了本课知识抽象的难点问题。】

二、图形推算落实重点——从学习的过程角度出发

【设计预期】本课的教学重点是，经历推理和探究几组图形之间相差关系的过程，渗透等量代换的思想，启蒙代数思维。为此，我们必须寻找一种合适的手段来落实这个教学重点。教师在不同的教学环节运用图形的推算，为学生提供了掌握本课重点的学习平台，也就是在代入（换）使一个等式中只有一个未知图形后，计算出等式中所含的图形，最终计算出另一个图形。这样就能在图形的推理运算中落实本课重点。

【教学实施】

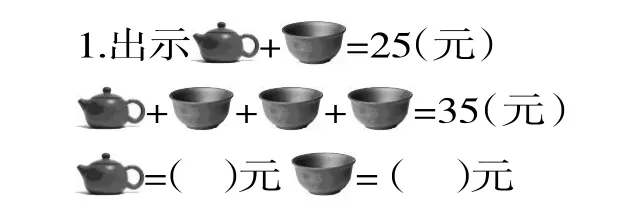
师：看着这幅图你知道了什么？像现在这样的情况还能继续“换”吗？

师：请仔细观察和比较：上下两行的总价为什么会相差10元？相差的10元表示什么物品的价格？

学生独立思考，尝试解决。引导学生汇报交流，同时用电脑演示“换”的过程，求出一只茶杯的价格。

小结：通过比较上下两个算式，“换”掉相同的部分，使算式中只含有一个未知数，这样我们就能计算了。

师：35元又包括了什么？如果我们从这个信息入手，又该如何来求得茶壶的价格呢？

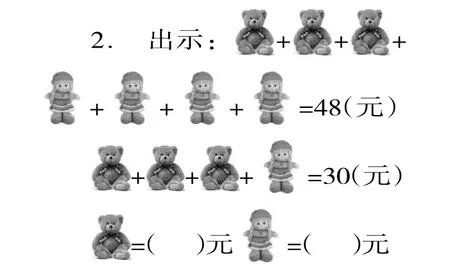
师：说一说从图中你知道了什么？

独立解题，交流思考的方法。

学生交流，教师追问：为什么两次价格不一样？相差多少？为什么第二次比第一次少花18元？18元包括什么东西？

列出算式：（48-30）÷（4-1）=6（元）洋娃娃；

（30-6）÷3=8（元）小熊。

小结：讨论解决这类问题，最关键的是什么？让学生在图形推算中明白这类题目的推算重点，一个算式中最后只能有一个未知的图形，才能计算出它的具体数据。

【实践成效：第1题，教师半扶半放，以扶为主。让学生对于这类题目有一个自己尝试解决的机会，在教师的帮助下学会用“换”的方法去将一个算式中的两个图形变成一个图形，感悟到只要一个等式中只有一个图形了就能计算出这个图形等于几了。第2题，教师由扶到放。让学生充分理解不仅一个图形可以“换”，一组中的多个图形我们也可以把它看成一个整体来换。小结环节在比较和提炼中，抽取数学模型。】

三、抽象建模实现拓展——从学习的方法角度出发

【设计预期】本课教学的灵魂是抽象建模，首先是让学生建立一种解决此类问题的模型，就是用“换”的方法将一个等式中的几个图形变成只有一个图形，从而计算出这个图形；其次要让学生树立一种意识，就是遇到此类问题是需要我们去思考和推理的，只要方法合适就会得到我们需要的答案。为此，特别进行了拓展提升练习，让学生在体会两次代换中慢慢建立模型，实现本课知识点的拓展、实现学习策略的提升。

【教学实施】

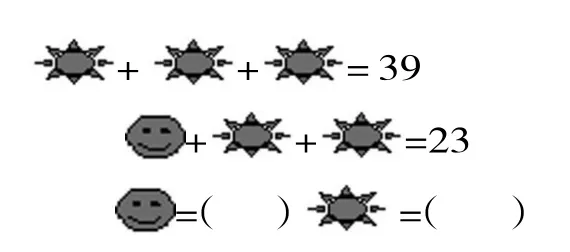
师：你还能用前面学过的方法解决这题吗？遇到了什么新问题？

师：不能通过两个算式“换”掉其中一个图形，怎么办？不换了吗？

学生独立思考。

师：你觉得这道题的思考方法和前面几题有什么相同点和不同点？

【实践成效：在逐步解决拓展练习中遇到的问题时，学生不仅得以沿用例题所学习的方法，而且锻炼了学生遇到与例题不一样的问题时应该如何去思考的能力，如何将看似不会的问题变成自己能够解答的问题，如何将复杂的问题变成比较简单的习题。在这样的训练中使得学生能够明白，当我们思考问题时，要尝试从不同的角度去观察和思考。】