对比解读教材引领有效教学———以《有余数除法》教学为例

徐建丽

解读教材的方法众多，笔者认为，把同一版本修订前、后的教材进行对比解读，找出变化之处，厘清改动本意，探求教学启示，也是非常有价值的。本文以人教版教材中《有余数除法》一课的教学内容为例，谈谈如何通过对比解读教材来引领有效教学。

一、对比解读，关注变化

仔细研读新旧教材关于“有余数除法”教学内容的编排，发现主要在以下五个方面发生了较大变化。

1．调：旧教材《有余数除法》是三年级上册第四单元的教学内容，现在调到了二年级下册第六单元。

2.分：旧版教材中，这一单元的教学安排5个课时的内容；而新版教材中，这一单元的教学安排了7个课时的内容，具体如下：

2001年　2014年内容　课时　内容　课时表内除法竖式的意义　1　认识有余数的除法　1有余数除法的竖式、余数的含义　1　余数和除数的关系　1有余数的除法练习课　1　认识除法竖式　1有余数除法的应用题　1　用竖式计算有余数的除法　1有余数除法应用题练习课　1　解决问题（一）　1解决问题（二）　1小小设计师　1

新教材编排有较大的变化，把认识余数的除法、理解余数和除数的关系分为2课时。第1课时着重于理解有余数除法的意义，第2课时着重理解余数与除数的关系，第3、4课时才真正学习有余数除法的计算方法。除法竖式学习从第1课时调整到第3课时。

3．换：旧教材的情境采用的是关于“摆花盘布置会场”的主题（图1），新教材以“摆图形”、“分草莓”的活动导入（图2、图3）。

图1

图2

图3

4．补：旧教材中在认识余数意义之后的“做一做”为两道式子计算，在“理解余数与除数的关系”之后的“做一做”是三道算式辨别题（图4）。

图4

新教材中的在“认识余数意义”之后的“做一做”是“圈一圈，填一填”，学生通过圈、填、写，理解有余数的除法算式。在理解余数与除数的关系之后的“做一做”是一道开放题，用一堆小棒摆五边形，探究余数可能出现的情况（图5）。

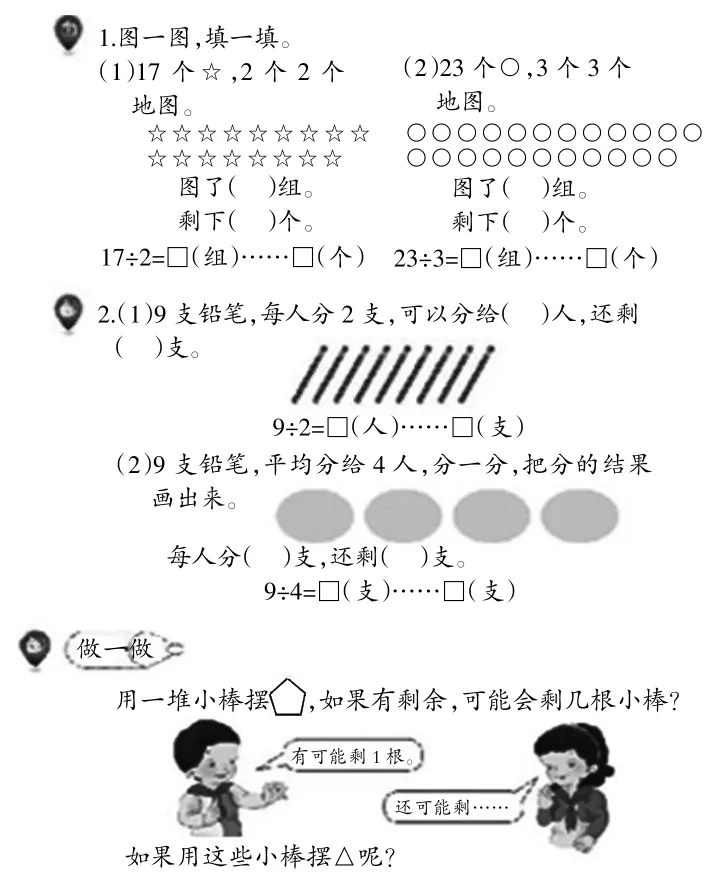
图5

5.拓：旧教材的应用练习题以有余数除法的计算为主，形式以填空、竖式计算、判断改错、简单问题解决为主。新教材除了以上内容，还拓展了“周期问题、租船问题、租房问题”等，拓宽了有余数除法应用研究的时空。

二、分析原因，厘清意图

新教材对旧教材做了五处改动。为什么会有这样的改动？改动背后隐藏着怎样的理念与意图呢？

1援新教材更加注重意义本质。

新教材将本节课从三上移到二下，让学生在学完《表内除法》后接着学习《有余数除法》——通过比较“平均分分完了与平均分后有剩余”的不同，突出了余数的本质意义。教材中没有出现“有余数除法”的严格定义，而是采用直观描述的方法进行介绍,以问题“余数表示什么”引起思考。对此，我们有必要了解什么是有余数除法。

“有余数除法”的概念在《小学数学基础理论和教法》中被定义为：“已知两个数a、b（b是自然数），要求两个整数q、r，使q、r满足以下条件：a=bq＋r，r＜b。这样的运算叫做有余数除法。一般记作：a÷b=q…r，读作：‘a除以b等于q余r’。”理解有余数除法的同时，不得不提起与有余数除法直接相关的一个定理——整除定理：设a、b是两个给定的整数，且b≠0，如果存在唯一的一对整数q与r，满足a=bq＋r，0≤r＜a。那么，b|a的充要条件是r＝0。如此看来，整除与有余数除法这两个概念是并列关系而不是包含关系，不能把整除看作特殊的有余数除法（余数为0）。

2.新教材更加注重操作体验。

过去，对有余数除法的教学往往倚重于计算，而不是把重点放在意义的理解上。新教材将教学内容在课时上一分为二，“余数的含义”以及“余数和除数的关系”分成2个课时学习，除法竖式学习从第1课时调整为第3课时，在余数意义理解之后再学习。这样的编排，突出了对余数除法意义的理解。

新教材比旧教材更加注重操作体验。旧教材给学生的感觉是有余数除法就是计算题，只要会计算就可以了，显然这样的理解是有失偏颇的。新教材非常注重学生操作活动的设计并提供了大量的素材，通过摆图形、分草莓、分铅笔等多个、多次分物活动，引导学生把直观形象与抽象概括相结合，采取边说边操作，边讨论边操作等方式，让手、脑、口并用，获得数学活动经验。大量操作活动的设计，不仅帮助学生亲身体验，积淀直接的抽象经验和归纳演绎的经历，而且更好地实现了横向数学化。

3.新教材更加注重难点突破。

有余数除法的结果涉及“两个单位”，这是正确理解有余数除法意义的一个难点。相比旧教材，我们会发现新教材有意识地让学生结合具体情境，通过直观解释，帮助学生克服单位填写的困难。新教材中有余数算式的出现，大多是“情境——操作——算式［□÷□=□（ ）…（ ）］”的模式，单位已经标注，通过填写单位名称和答案，引导学生在多次关注中加深理解余数除法的意义。

三、理解变化，有效教学

1.重视有余数除法的教学价值。

在小学教学中，有余数除法是常见的运算，它不仅存在于多位数除法的计算过程中，而且应用于解决周期问题中。初等数论的证明中最重要、最基本、最常见的工具是有余数除法，也称为除法算法。有余数除法的重要性不只是体现在算术计算中，而且也是数论证明的重要工具。所以，有余数除法不能只作为计算的一部分内容，只要求学会算题，而应该充分重视其价值，理解其意义。

2.经历数学化过程，发展建模能力。

“有余数除法”是小学数学教学中数学化的经典课题。弗赖登塔尔说：“用数学方法把实际材料组织起来，这在今天叫做数学化。”将非数学的内容数学化，就是将这些内容组织成合乎数学准确性要求的结构。

在课堂教学中，教师可以通过苹果、草莓、小棒、豆子等实物，来帮助学生理解余数概念。

【片断一】

师：请大家把9个苹果平均放到3个盘子里，先动手分一分，再用算式表示，并解释算式的意义。

生：（动手分后）9衣3=3。

师：（1）把9个苹果平均放到2个盘子里，动手分。能否用算式来表示呢？（2）将9个苹果平均分到4个盘子中，动手分，用算式表示，并解释意义。

生：9衣2=4多1，9衣4=2多1。

师：我们通常用这样的算式来表示，9衣4=2…1。谁来解释这个式子的意义？

要分的苹果数 盘子数 每个盘子中的苹果数 剩余的个数

师生归纳余数的概念。

上述片断的教学核心，在于帮助学生经历现实问题数学化的过程，获得数学建模的直接经验和体验，完成建模过程，即现实问题——数学问题——数学问题的解——现实问题的解。

3.寻找规律，理解规则。

余数为什么要比除数小？教师通常引导学生这样思考，以分物品的活动为例，“如果余数比除数大了就还可再分”。其实，这样解释既不符合生活现实，也不符合数学逻辑。如果没有规定余数要比除数小，那么就会有不同的计算结果，这在数学中一般是不允许的。因此余数要比除数小，是为了保证计算结果的唯一性。如何让学生理解这一规定呢？

【片断二】

师：用8根小棒摆正方形，能摆几个？

生：摆2个。8衣4=2。

师：先想一想，有9、10、11根小棒的话，可以摆几个正方形，还剩几根小棒？再用算式表示。

生：9衣4=2…1，10衣4=2…2，11衣4=2…3。

师：观察以上三个算式，你能接着写出下一个算式吗？

生：12衣4=2…4。

师：你是怎么想的？

生：被除数增加1，余数也增加1。

师：是这样吗？有不同的想法吗？

生：12衣4=3，没有余数。

师：为什么余数没有了？

生：余数有4根，就可以再摆一个正方形了（用12根小棒操作一次）。

师：照这样的规律继续往下写，你能写出哪些算式呢？

生：13衣4=3…1，14衣4=3…2，15衣4=3…3。

师：请观察以上6个算式，有什么规律？关注余数的变化，你发现了什么？

生：除数都是4，余数都是1、2、3。

生：余数都比4小。

师：真的吗？交流一下，这是为什么？

生：余下如果有4根，就可以摆成一个新的正方形。

师：用一堆小棒摆五边形，如果有剩余，可能会剩几根小棒？

……

上述片断的教学核心，在于学习的素材是两组各3个有联系的除法算式，算式除数、商相同，相似度高，学生自然而然会把注意力集中到被除数有序变化，余数有序变化，很快发现余数周期性变化的规律。学生发现了这个变化的周期，也就容易理解余数要比除数小了。

综上所述，通过对同一版本的前、后修订教材的对比解读，我们可以比较准确地把握教材的设计意图，在此基础上再进行一系列的分析思考，如素材是否需要调整，是否需要补充，怎样对教材素材进行二次加工、开发等，不仅能够促使我们合理有效地用好、用活教材的素材，抓住数学本质，而且可以通过大胆地对教材的呈现方式进行适当加工、改造、优化或重构，做到创造性地“用教材”。