研究课本例题编写意图,提升课堂教学水平
2016-03-30施莉莉
施莉莉

摘 要:数学例题是连接数学理论与数学实践的桥梁,学生通过例题来建构数学知识、感受数学应用,因此课本的例题在编写时具有示范性、承启性、探究性和发展性,教师在课堂教学时,要能够恰当地挖掘出这些例题的编写意图,讲全、讲深、讲透,提高课堂教学效率.
关键词:例题;编写意图;课堂教学;苏教版教材
例题是“用来说明某一定律或定理,或在运用某一学科或学科分支的定律时充当练习的题.” 可见,例题是教科书概念、命题和定理与习题之间的桥梁与纽带,例题教学的成功与失败直接关系到学生对数学知识的建构、对解题方法的掌握. 因此,我们数学教师在备课时研究揣摩教科书例题的编写意图,全面领会编写者的理念,这样才能在课堂教学时,把例题讲全、讲深、讲透,全面发挥例题的功能,提高教学效益.
巩固型例题,要发挥解题的示范性
课本上例题的最主要功能是巩固本节所学的数学理论知识和方法,例题的编写不是随意的,编者在选择时经历了反复的推敲,因此有着极强的示范性和典型性. 教师在教学中,要注意发挥典型例题示范性,做到易题详讲、小题大讲,这样做的目的一是教师思维模式示范,二是解题格式的示范,三是解题反思与优化的示范.
案例1 (必修4,1.2.3 三角函数诱导公式,例4)
首先,应向学生示范分析问题的过程,这个分析的过程正好是教师思维的过程.老师拿到题是怎么想的?肯定是先观察,发现75°+α和15°-α之和是90°特殊角,这样正好可以利用“诱导公式五”,把所求的cos(15°-α)转化成sin(75°+α)解决.
其次,向学生示范解题的过程,由于学生对角的取值范围易忽视,因此教师要特别注意,对角取值范围的书写,教师省略一个步骤,学生就可能省去数个步骤.
由-180°<α<-90°,得-105°<75°+α<-15°,则sin(75°+α)<0.又cos(75°+α)=,所以cos(15°-α)=cos[90°-(75°+α)]=sin(75°+α)=-= -=-.
再次,向学生展示解题后,如何反思与优化解题过程,这是提高解题水平的关键一环. 本题的解决依赖于观察,看到所求三角函数值的角与已知三角函数值的角之和为90°,如果观察不出来怎么办?抑或更为复杂的关系怎么解决?这里要提炼,要向学生讲述反思的过程. 观察的实质是把“75°+α”看成整体,看成整体是换元的思想,因此可以设75°+α=β,即α=β-75°,所求的三角函数的角15°-α=15°-(β-75°)=90°-β,于是原题就转化成已知cosβ,求cos(90°-β),应该说,换元法更具备一般性.
通过这样的“三个示范”,学生不仅巩固了新学的诱导公式,而且学会了思考、学会了表达,也掌握了解决这类问题的一般方法. 真正体现减少训练、提高效率的作用. 这个案例也告诉我们,每讲一道例题都应当问一问为什么要讲它?它“范”在哪里?“例”在何方?学生从中能够学到什么?
承启型例题,要展现知识的系统性
由于数学知识是一个有机的整体,后续的知识往往是前面知识的延续的发展,因此课本上的例题有时还起到“承上启下”的作用,它既是已经学习知识的应用,也是将来学习知识的缘起,因此教师在教学时要能够洞察到这类例题的作用,这样不仅可以使课堂教学顺利过渡,也可以强化学生对知识系统性的认识,建立起完整的知识结构,而不是一堆离散的知识点.
案例2 (必修1,2.1.1 函数的概念和图象,例5)
在第2.1.1开头的问题第一个问题中,如果把人口数y(百万)看作是年份x的函数,试根据下表,画出这个函数的图象.
经过仔细研究发现,这个例题编写的目的至少有三个:第一它是本节开头的背景问题,是引入函数概念的主要问题之一,让学生体会函数两个量之间的对应关系,在后面第3.4.2节函数模型及其应用学习中还将深入讨论;第二该问题在第2.1.2节中,用来说明列表法也能表示函数,并且函数图象可以是离散的点,这与以前学生所见的大多数函数图象稍有不同,这有助于更新学生的认识观念;第三,这个问题,还为接下来函数单调性的学习做好铺垫.
由此可见,一个普通的例题,不仅是概念背景问题的延续,也是继续学习的基础,贯穿了函数的概念、函数的图象、函数的表示和函数的应用. 如果教师在教学中把该例题跳过了,势必造成教学上的不连续,甚至学生对知识连续性的认识不到位. 这样的案例在教材中还有很多,再如第1.2节的例2:
下列各组的3个集合中,哪两个集合之间具有包含关系?
粗看可能平淡无奇,有的老师可能认为不够好,另选其他例题,事实上本例的每一组3个集合中,A,B这两个集合没有公共元素,且它们的元素合在一起,恰好是集合S的全部元素,这个思考为学生感受和理解补集、全集的概念奠定基础,也为从集合运算的角度理解补集做铺垫.
像这样的例题的编写意图,需要教师仔细揣摩才能发现,这需要教师加以研究,尽可能地发挥集体的智慧,在集体讨论的基础上相互启发,才能集思广益,发现编者用意.
结论型例题,要展示问题的探究性
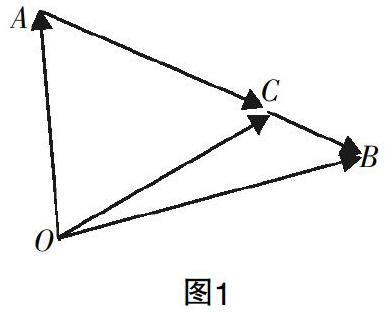
课本上还有很多例题本身就是一个常用的结论,甚至在以前老版本的教科书中是作为定理或者公式给出的,在新课标教材中,只是为了降低学习的难度和减轻学生的负担才淡化成例题的.如定比分点公式(见必修4,平面向量坐标运算例4)在老的人教版教材中是作为公式出现的,现在苏教版中就作为一个例题. 对于这样的问题,尽管结论本身,不能够在解题中直接使用,但是教师也要能够像其他概念、公式、定理一样,舍得花时间,让学生进行探究,弄清来龙去脉.
结论中当λ∈R且λ≠-1时,=是线段定比分点的向量公式,若改写成=+,就是A,B,C三点共线的条件.
这里可以让学生分三个层次进行探究活动:
(1)证明方法的探究:即如何从=λ向结论进发?
(2)逆命题的探究:一般地,若存在两个实数s,t,且s+t=1,使得=s+t,则A,B,C三点共线.
(3)点C位于线段AB上与位于线段AB延长线上或线段BA延长线上,λ的取值有何不同?
(4)本例题在题干的表述上是有瑕疵的,请指出.
值得一提的是本例题的教育价值除了证明过程能够巩固加强“向量共线定理”、结论能够为学生的探究性学习提供素材外,还有以下的价值:
(1)直线AB上任一点C都能够用OA,OB来表示,有助于提出问题:“是否平面上任一点C都能用OA,OB来表示”,这为下一节平面向量基本定理学习激发学习动机;
(2)为下面“平面向量的坐标运算”中定比分点公式和中点公式推导打下基础;
(3)可以类比到选修2-1中“三个向量共面”的充要条件.
结论性例题的一个教学误区是让学生死记结论,对于学生来说,他们要记忆的材料太多了,因此单纯的记忆是行不通的,即使记住了,也不会应用. 这类例题是开展探究性教学的最佳材料,通过探究,学生掌握了结论的来龙去脉,不仅知道它是怎么产生的,也知道应用到何处去.
方法型例题,要重视思维的发展性
课本中的例题,除了知识性问题,还有方法性的问题.这类例题为师生提供了通解通法,展现了一般解决问题的思路,教师在教学时,要能够通过这样的问题让学生学会数学的思考,程序化解决问题,培养学生理性思维能力.
本例题虽然是非常基础的问题,但是这两种解法,实际上是从两个不同的角度解决了求切线方程的问题. 方法1是几何法,利用了“直线与圆相切”等价于“圆心到直线距离等于半径”这一特征,方法2是代数法,主要是从直线方程与圆的方程联立后有两相等根这一性质. 很多师生对课本第二种解法不够重视,认为计算量大,过程烦琐,就一跳而过,这是错误的. 尽管方法2计算烦琐,但教学中更需要重视,因为解法2更具有一般性,为后面学习直线和其他曲线位置关系奠定基础. 因此教师在方法类例题的讲解中,应体现从具体到抽象,从特殊到一般的思维过程,以及归纳、总结的一般方法,这样更加有利于学生思维的发展.
除了上面所述的类型例题外,还有应用型的例题,教学中应展现其科学性和人文性,让学生体会到数学的科学价值和人文价值. 有的例题,还要综合发挥其作用,如上面提到的案例3,除了展现其探究性,也要让学生认识到知识的连续性与综合性. 所以有人说“教师与其糊里糊涂地讲一百例题,还不如清清楚楚地讲清一道题”就是这个道理.
