从n=k到n=k+1的技巧

罗邯



从n=k到n=k+1的技巧

罗邯

不等式的证明有多种方法，涉及到与正整数有关的不等式时，可考虑用数学归纳法。证明过程中除了要严格按照数学归纳法的证明步骤外，最关键之处是如何从n=k推出n=k+1时，不等式也成立。本文介绍几种从n=k到n=k+1的技巧，教师们在教学时，可以适时地教给学生，提高他们的解题能力。

解析从左边式子观察可知，由n=k到n=k+1后，起始项变为，则减少了一项，末项应为，又中间项的分母为连续正整数，因此应增加

两项，故选B。

点评一定要仔细观察不等式的结构，发现从n=k到n=k+1时增加了多少项，减少了多少项，一般用（fk+1）-（fk）来研究，才能准确无误。

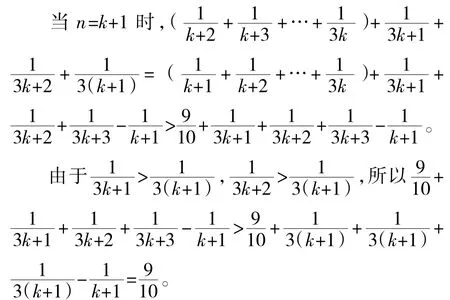
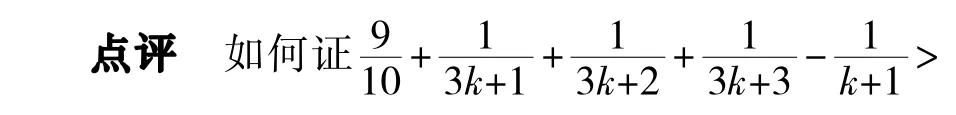
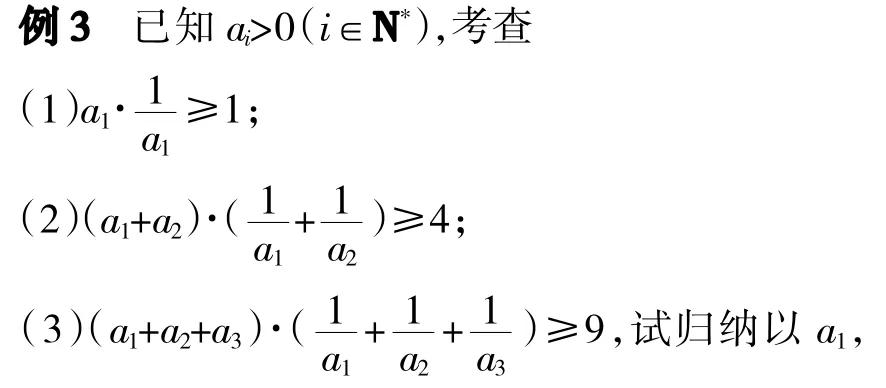
a2，a3，…，an也成立的不等式，并用数学归纳法证明。

解析由已知，归纳猜想得（a1+a2+a3+…+an）·

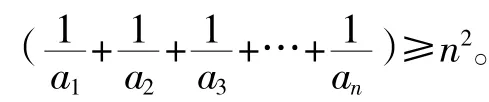
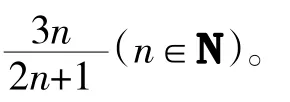
点评：证明n=k+1时结论成立，可以采用分析法，找到解决的办法。如本题就没有放大或缩小不等式，是采用分析的思路、作差的方法解决的。

在数学归纳法证明不等式的过程中，综合性较强，要会观察，善思考。由假设n=k成立，推证n= k+1时也成立时，证明用上归纳假设后，可采用分析法、综合法、比较法、放缩法，基本不等式法等证明。因此，用好了数学归纳法，就可证好不等式。

（作者单位：浏阳市第一中学）

《湖南教育》“潇湘数学组”栏目策划

数学组，无疑是整个学校数学教学的智囊团。数学组所获得的重要成果，直接决定着整个学校数学教学的风格和水平。风格独特、水平高超的数学教学，正是我们一以贯之所支持的，也是我们向全省数学教师推介的首要原因。如果你们的数学组有特色，那么来亮亮你们的数学组吧。请准备好以下材料：

1.数学组全体人员全家福照片一张；

2.数学组具有重大意义的教学讨论成果；

3.数学组认为本组最好的一堂课的实录；

4.数学组的一次颇有意义的集体备课成果；

5.数学组关于某些教学难点的处理方法（如小学的分数、初高中的函数等）；

6.数学组所获得的一些教学金点子；

7.数学组的课题成果；

8.数学组成员的优秀论文。

如果你们觉得还有拿得出手的其他成果，也可以形成文字材料。

我们将秀一秀你们数学组的风采。请联系：

李闯QQ：415897894，邮箱：lichuangde520@126.com

徐旺QQ：474950007，邮箱：zyb0522@126.com

探索