次数公式在整系数多项式不可约判别中的应用

陈益智，蔡俊树，肖裕耿

（惠州学院数学系，广东 惠州 516007）

次数公式在整系数多项式不可约判别中的应用

陈益智，蔡俊树，肖裕耿

（惠州学院数学系，广东 惠州 516007）

本文利用多项式的次数公式探讨了三类整系数多项式在有理数域上不可约的判别与证明。

次数公式；整系数多项式；不可约多项式

多项式是代数中的一个基础概念，也是高等代数中的主要内容之一。而作为多项式理论的一个重要的知识点，整系数多项式在有理数域上可约性的判别经常出现在一些高校《高等代数》课程的硕士研究生入学考试试题中。一直以来，也有不少文献（如参见文献[1-8]等）对整系数多项式可约性的判别进行研究，而大多数文献中不可约多项式的判别是利用艾森斯坦判别法。

本文利用多项式的次数公式及多项式的在某处的取值，着手探讨三类整系数多项式在有理数域上可约性的判别与证明，旨在给读者提供判别多项式不可约的一种有效求解方法。其中a1, a2,…,an为互异整数，则f(x)在有理数域上为不可约多项式。

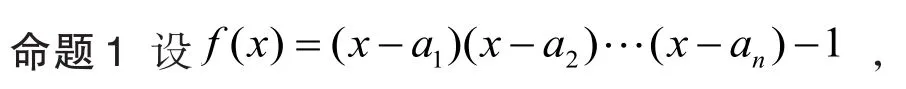
证明：显然，f(x)为整系数多项式。假设f(x)在有理数域上可约，则∃g(x), h(x)∈Z[ x]，使得

由于f(x)=(x-a1)(x-a2)…(x-an)-1，所以g(ai) h(ai)=-1，i=1,2,…,n .

因为g(x), h(x)为整系数多项式，所以g(ai),h(ai)只能互为±1。从而有于是，g(x)=-h(x)。从而f(x)=-g2(x)。这与f(x)首项系数为1矛盾。故f(x)在有理数域上不可约。

注1由该命题的证明过程，我们可以看出次数公式在判别整系数多项式在有理数域上不可约的作用，从而避免了利用艾森斯坦判别法来寻找素数p 的难处。

命题2设f(x)=(x-a1)(x-a2)…(x-an)+1，其中a1, a2,…,an为互异整数，则有：

（1）当n为奇数时，f(x)在有理数域上为不可约多项式；

（2）当n为偶数时，f(x)在有理数域上的可约性不确定。

证明：显然，f(x)为整系数多项式。假设f(x)在有理数域上可约，则∃g(x), h(x)∈Z[ x]，使得

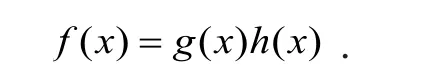
由于f(x)=(x-a1)(x-a2)…(x-an)+1，所以

因为f(x)为整系数多项式，所以g(ai),h(ai)只能同为1或-1。从而有

又因为

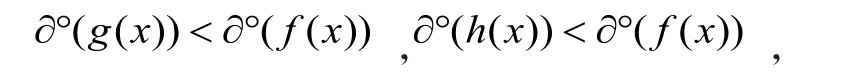
所以

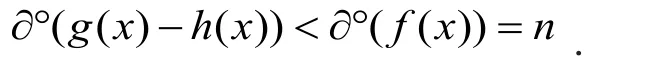
注意到g(x)-h(x)=0有a1, a2,…,an这n个根，所以

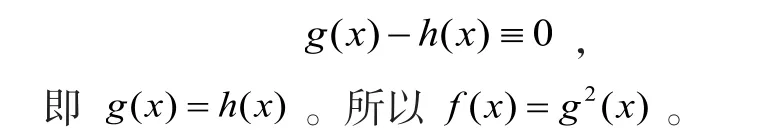
a）当n 为奇数时，f(x)=g2(x)与f(x)的次数为奇数矛盾，故f(x)在有理数域上为不可约多项式，

b）当n 为偶数时，f(x)在有理数域上的可约性不确定。这是因为若取n=2，a1=1，a2=-1，则f(x)=(x-1)(x+1)+1=x2。此时f(x)在有理数域上为可约多项式。若取n=2，a1=1，a2=2，则f(x)=(x-1)(x-2)+1=x2-3x +3。此时令p=3.则由艾森斯坦判别法可知，f(x)在有理数域上为不可约多项式。

综上，当n 为偶数时，f(x)在有理数域上的可约性不确定。

注2该命题与命题1类似。同样，命题2（1）若是要利用艾森斯坦判别法，则很难找到素数p，而利用次数公式来探讨该问题，f(x)在有理数域上的可约性则可迎刃而解。

命题3设f(x)=(x-a1)2(x-a2)2…(x-an)2+1，其中a1, a2,…,an为互异整数，则f(x)在有理数域上为不可约多项式。

证明：显然，f(x)为整系数多项式。假设f(x)在有理数域上可约，则∃g(x), h(x)∈Z[ x]，使得

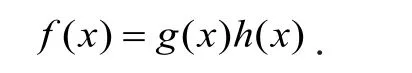
因为f(x)为整系数多项式，所以g(ai),h(ai)只能同为1或-1。又注意f(x)＞0恒成立，所以f(x)=0没有实根。因此g(x), h(x)也没有实根，故g(ai),h(ai)(1≤i≤n)只能恒为1或-1，否则由数学分析中函数的连续性定理可知，必∃x′∈R，使得g(x′)=0或h(x′)=0成立，也与f(x′)=0矛盾。

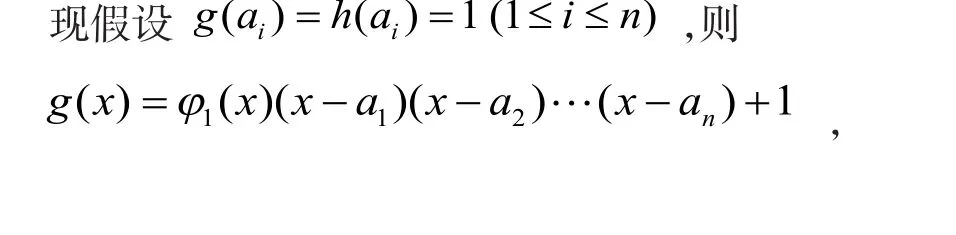
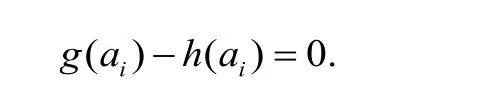
h(x)=φ2(x)(x-a1)(x-a2)…(x-an)+1，其中φ1(x),φ2(x)为整系数多项式，且1≤i≤n 。

由次数定理我们有：∂°(f(x))=∂°(g(x) h(x))=n ，即∂°(f(x))=∂°(h(x))+∂°(g(x))=n .又∂°(h(x))≥n ，∂°(g(x))≥n ，所以∂°(h(x))=n ，∂°(g(x))=n ，即∂°(φ(x))=0，∂°(φ(x))=0，所以φ1(x)=φ2(x )=±1。不管是哪种情形都有f(x)≠g(x) h(x).这与假设矛盾，故f(x)不可约。

注3该命题中，f(x)的一般形式是较难表示出来的，所以要通过艾森斯坦判别法更是难上加难。利用次数公式从反面推出矛盾，则可解决该题。

综上，本文利用多项式的次数公式探讨了有理数域上三类整系数多项式可约性的求解。而这几种类型题在近几年的高等代数考研试题中屡有出现。例如：命题3为2013年深圳大学的高等代数考研题，命题1为2014年的华南师范大学的高等代数考研题。而针对这些类型的多项式都可使用本文的方法来证明其为不可约多项式。

在此，我们希望通过本文对这些类型题的探讨能引起人们对这种方法的重视。

[1]张卫，史滋福.有理数域上的一类不可约多项式[J].湖南理工学院学报，2008，21（1）:5.

[2]刘中良.有理数域上多项式不可约的判定[J].科技信息，2009（1）：163.

[3]巩娟.整系数多项式在有理数域上不可约判别法[J].辽宁师专学报，2009，11（3）:35.

[4]陈丽.有理数域上多项式不可约的判定[J].安庆师范学院学报：自然科学版，2009.15（3）:80.

[5]陈侠.关于整系数不可约多项式[J].沈阳航空工业学院学报，2009，11（3）:35.

[6]兰春霞.整系数多项式在有理数域上不可约的几个判定定理[J].丽水学院学报，2005，27（2）:13.

[7]陈雪雯，吴晓红.整数环上的不可约多项式[J].高等数学研究，2010，13（1）:22.

[8]殷晓斌，吴俊.一类整系数不可约多项式[J].高等数学研究，2013，16（1）:1.

[9]张禾瑞.高等代数[M].第4版.北京:高等教育出版社，1999.

【责任编辑：吴跃新】

Applications of Polynomial Degree Formulas in Judging Irreducible Polynomials

CHEN Yi-zhi，CAI Jun-shu，XIAO Yu-geng
（Department of Mathematics，Huizhou University，Huizhou 516007，Guangdong China）

In this paper，the reducibility in rational field of three kinds of integral coefficients polynomials is discussed by using polynomial degree formulas.

polynomial degree formula；integral coefficients polynomial；irreducible polynomial

O151.2

A

1671-5934（2016）03-0070-02

2016-05-11

广东省高等教育教学改革项目（GDJG20141242，粤教高函[2015]173号）；广东省教育科研项目（2013JK168）；广东省教学成果

培育项目：高师数学专业人才培养模式的创新与实践（粤教高函[2015]72号）；惠州学院教学成果培育项目（CGPY2014001）

陈益智（1980-），男，广东龙川人，副教授，理学博士，研究方向为代数学及其应用。