多重同心圆TSP问题的研究
2016-03-29廖迁彭刚
廖迁,彭刚
(惠州学院计算机科学系,广东 惠州 506007)
多重同心圆TSP问题的研究
廖迁,彭刚
(惠州学院计算机科学系,广东 惠州 506007)
旅行商问题(TSP)是一个典型的组合优化问题,具有相当广泛的应用价值,对于实际的生产生活具有重要意义。多重同心圆TSP问题为TSP问题中的一个特殊的例子,运用遗传算法,求解多重同心圆TSP问题,可以对其他优化问题的求解提供参考方案,同时也可以用于对不同算法进行比较。本研究重点着眼于同心圆的个数、城市数目、迭代次数等对算法的影响。
TSP;遗传算法;多重同心圆
1 引言
TSP问题是数学上一个典型的组合优化问题,可
以描述为[3-4]:指定N个城市(C=c1, c2,...,cn),商家从任意一个城市开始出发,不重复地经过每一个城市,最终回到出发城市,按照要求找出商家能够尽可能地降低成本(时间成本、经济成本等)在所有城市之间巡回的最短路径。在现实的生产生活中,电路板路线印刷、管道铺设以及物流配送等问题,均能转变成TSP问题的模型,如果TSP问题能够被有效地解决,人们的生产生活效率能够大大地提高,节省大量的资源。
本研究主要通过控制变量法,利用遗传算法具有并行性,随机性等特点,来研究不同因素对算法的影响。本研究对现实的TSP问题进行参数编码、通过迭代方式对编码后的染色体进行遗传操作来交换群体中染色体的信息,形成新的个体,最后把符合优化目标的个体保留下来,即为所求算法的最优解。
2 求解多重同心圆TSP问题的遗传算法
2.1 多重同心圆遗传算法基本实现方法
研究多重同心圆TSP的问题时,在二重同心圆的基础上,增加适应多重同心圆的优化选择的方法。由于在多重同心圆上,内外圆之间的距离与圆上相邻两个点之间的距离比较接近,因此选择在这种情况下更加合适的优化算法:路径比较法。
所谓路径比较法[1-2],就是在随机选择的四个点中,两两相连,计算并判断连线的长度,获取不重复地连接四个点的两条连线,即为经过四个城市的最短路径。如图所示:

图2 优化后路径图
其步骤如下:
Step1:选择一条路径C={C0, C1,...,Ci, Ci+1,...,Cj, Cj+1,...,Cn-1},随机找出不规则的四边形CiCi+1CjCj+1。
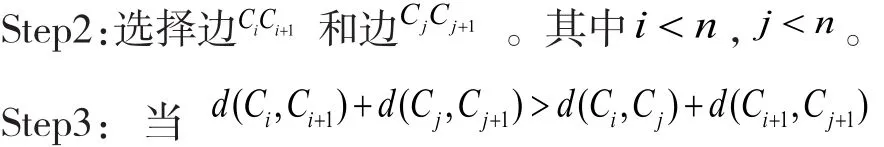

2.2 算法流程
相比于基本遗传算法,上述算法加入了适应多重同心圆TSP问题的路径比较法,其算法流程如下:
Step1:随机地产生个体数为N的初始群体。
Step2:计算群体中个体的适应度
Step3:判断种群中个体是否满足终止条件,若满足,则终止算法,输出最优解;若不满足,则执行择优保留的选择操作。
Step4:进行交叉操作。
Step5:进行变异操作。
Step6:执行局部优化的路径比较法。
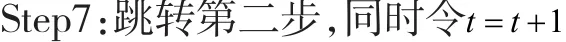
2.3 实验设计
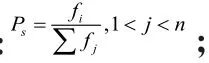
实验一:假定城市个数NG=240、迭代次数Generation=50不变,只改变圆的个数Circle。探究圆的个数不同时,算法的执行效率。
实验二:假定圆的个数Circle=8、圆的半径及城市个数NG=200不变,只改变迭代次数Generation,观察算法的收敛过程。
实验三:假定圆的个数Circle=8,城市个数NG= 160,迭代次数Generation=200不变,通过改变圆的半径,观察算法最优化时可能出现的图形。
实验四:假定圆的个数Circle=8,迭代次数Generation=200和圆的半径不变,改变城市个数NG(160-320),观察城市个数对算法效率的影响。
3 结果分析
3.1 实验一

表1 实验一结果统计
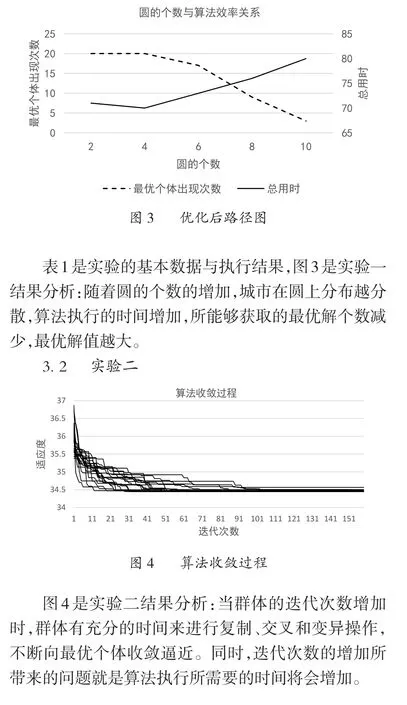
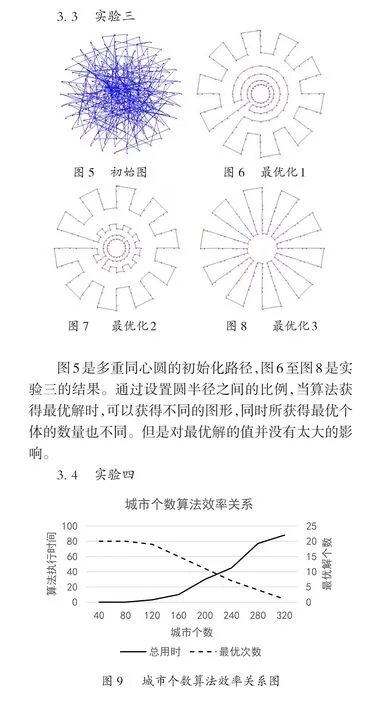
图9是实验四的结果分析:算法的执行时间与城市个数成正比,最优解个数与城市个数成反比。当群体规模增加时,算法计算所消耗时间相应增加,同时获得最优个体的数量相应减少。
4 结束语
实验结果表明:加入路径比较法的基本遗传算法,能够更加有效地求解多重同心圆的TSP问题,具有较强的全局搜索能力和局部搜索能力;实验所得图形也能够让我们更加直观地判断是否是最优解;同时也验证了遗传算法在求解TSP问题时,有较强的获取最优个体的能力。
[1]PENG Gang.Ichiro Iimura and Shigeru Nakayama.Application of Genetic Recombination to Genetic Local Search in TSP.[J].International Journal of Information Technology,2007,13(1):63-64
[2]PENG Gang.Ichiro Iimura and Shigeru Nakayama.An Evolutionary Multiple Heuristic with Genetic Local Search for Solving TSP.[J].International Journal of Information Technology,2008,14(2):4-5
[3]周敏.遗传算法求解TSP的研究.[J].无线互联科技,2015(3)129
[4]程林辉,李航高.遗传算法及其在TSP问题中的应用[J].现代计算机,2013,14(5):20
[5]郭峰,陈勇.改进的遗传算法求解TSP问题[J].现代计算机,2014,17(11):48
[6]方建斌.一种基于TSP的改进遗传算法设计与实现[J].现代经济信息,2015,23(2):322
[7]王松泉.遗传算法在组合优化中的应用研究.[D].合肥:安徽大学,2010
[8]曹道友.基于改进遗传算法的应用研究.[D].合肥:安徽大学,2010
Study on Multiple Concentric TSP Problem
LIAO Qian,PENG Gang
(Computer Science Dept.,Huizhou University Huizhou 516007 Guangdong China)
The TSP is a typical combinatorial optimization problem which is widely applied in our life.A Multiple Concentric Circle Problem which shows a regular shape is a special case in TSP.It is valuable for other TSP and comparison of different algorithms solving a Multiple Concentric Circle Problem by using the genetic algorithm combined with heuristic search method.This study emphasis on the efficiency of the parameters in the promising algorithm proposed in the experiment.
Traveling Salesman Problem(TSP);Genetic Algorithm(GA);Multiple concentric circle
TP39
A
1671-5934(2016)03-0062-03
2016-05-03
廖迁(1995-),男,广东梅州人,本科,研究方向为计算机应用。
