数学概念教学三原则
2016-03-28赵绪昌

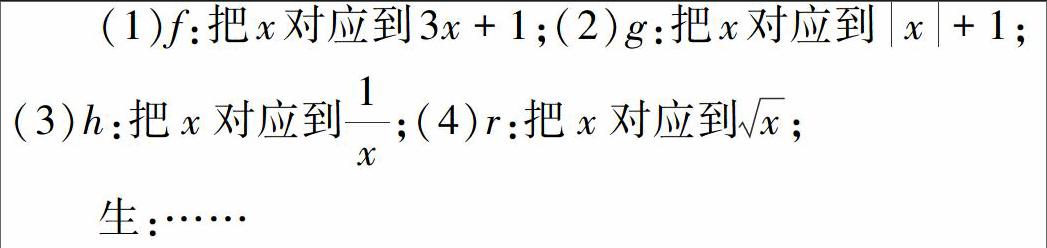
【摘 要】 学生对数学概念的习得与建构,总是基于丰富而深刻的数学体验基础上的.数学概念教学要注重三原则:感知要忌浅倡深,深入体验;抽象要忌快倡慢,渐进概括;巩固要忌听倡做,实践反思.从而实现在深度体验中建构数学概念.
【关键词】 数学概念;教学原则;案例分析
高中数学概念教学有些现象很令人担忧:教师重解题技巧,轻概念生成,追求概念教学最小化和习题讲解最大化;学生认为概念学习单调乏味而不重视它,对基本概念死记硬背、不求甚解,只是机械记忆.后果表现为学生在没有真正理解概念的情况下匆忙去解题,使得他们只会模仿教师解决某些典型例题的题型和掌握某些特定的解法,一旦遇到新的情况、新的题目就束手无策,进而导致教师和学生为了提高成绩,陷入无休止的题海之中.造成这种现象的主要原因,在于学生仅仅知道数学概念本身,并未理解概念的形成过程,对概念引出的必要性、概念的本质及其功能没有深刻的认识.《普通高中数学课程标准》指出:“数学教学中应强调对基本概念和基本思想的理解和掌握,对一些核心的概念和基本思想要贯穿高中数学教学的始终,帮助学生逐步理解.由于数学高度抽象的特点,注意体现基本概念的来龙去脉.在教学中要引导学生经历具体实例抽象数学概念的过程,在初步运用中逐步理解概念的本质.”学生建构数学概念总是基于自我体验基础上.学生只有获得丰富而深刻的数学体验,数学思考才有具体的经验支撑,数学概念才能得以有效建构.下面结合案例说明数学概念教学的三原则.
1 感知——忌浅倡深,深入体验
学生对抽象数学概念的建立,离不开感性经验的获得,数学感知也就成了学生学习数学概念的首要环节.而学生对感性经验的积累,源于对数学素材感知的深浅程度.匆促、肤浅的简单化感知,不利于学生对数学本质的触摸、积累.只有深入挖掘数学素材,引导学生循序渐进地从事观察、操作、比较、思考等深度的数学活动,才能积累丰富的数学活动经验,进而触及数学概念本质.
案例1 人教A版《数学2》“3.1直线的倾斜角与斜率”(第一课)的教学片断.
在介绍完倾斜角这个概念之后,我们需要引入另一个新概念——斜率,如何引入呢?教材中是直接规定的.“我们把一条直线的倾斜角α的正切值叫做这条直线的斜率”.如果在实际教学中也这样引入的话,学生会提出这样的质疑:为何要用正切值,而不能用正弦或余弦呢?面对这样的提问,有的老师会说这是统一规定;有的老师相对民主些,逐一验证为何正弦或余弦不好,但总给人“亡羊补牢”之嫌.
其实,完全可以通过设计下面两个小问题引入斜率的概念.
问题1 请在同一平面直角坐标系中画出下列方程所表示的直线.
师:问题2中的三条直线有何不同?
生:倾斜角不同,分别是45°,60°,135°.
师:大家发现了什么?
生:问题1中x前的系数恰好是问题2中对应的倾斜角的正切值.
师:这会是偶然现象吗?(此时,教师可利用“几何画板”演示当倾斜角变化时,直线倾斜角的正切值与直线x前的系数始终保持一致)
师:看来,直线倾斜角的正切值与直线方程息息相关,那么我们不妨用直线倾斜角α的正切值来刻画直线的倾斜程度,并给它取个名字,叫做直线的斜率.
评析 案例中,教师提出问题,通过学生思考、交流,加深了对“直线的斜率”概念的理解,逐步领悟其内涵,把握其本质. 这样的方式引入斜率的概念,自然、流畅,学生感知深刻,理解深入,把握本质.
2 抽象——忌快倡慢,渐进概括
从具体的感性经验中抽象出理性的数学概念,是数学认知水平的一大飞越,是概念教学的核心环节.而抽象概括数学概念,是学生不断地比较、剔除非本质因素,逼近概念本质的渐进过程.因此,抽象数学概念要忌快倡慢,要放慢教学节奏,引导学生多层多角度地对数学素材做出观察、比较、概括,参与概念的形成过程,深刻揭示抽象定律的特定内涵.
案例2 “函数概念”的教学片断.
师:下列问题中各含有哪些变量,它们之间的关系是用什么方式表达的?
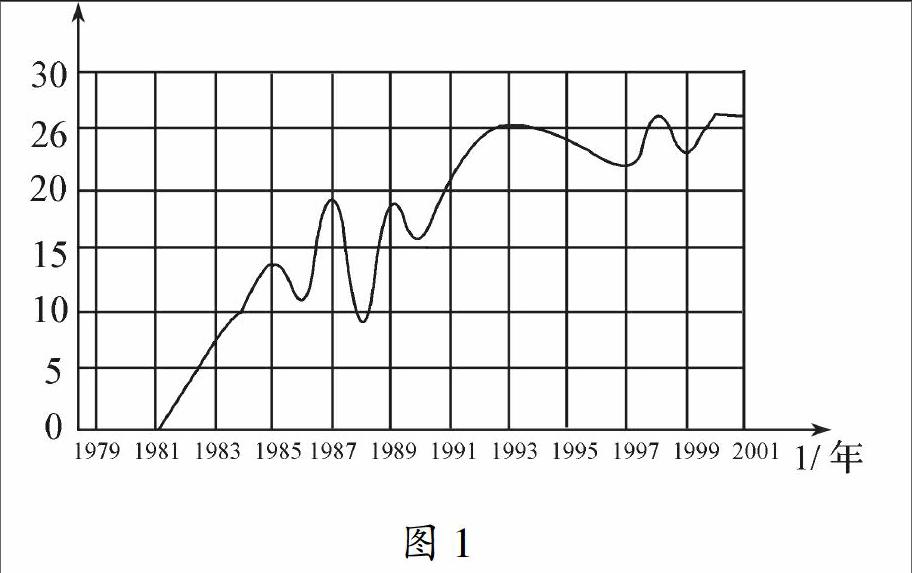
生:①中含有两个变量,分别是炮弹距地面的高度h(单位:m)及时间t(单位:s),它们之间的关系是用解析式表达的;②中含有两个变量,分别是南极上空臭氧层空洞面积及相应年份,它们之间的关系是用图像表达的;③中含有两个变量,分别是我国城镇居民恩格尔系数及相应年份,它们之间的关系是用表格表达的.
师:现在,我们来分析上述各题中两个变量的关系的特点.如①中,只要给定了时间t(0≤t≤26)的任意一个值,就唯一地确定了炮弹距地面的高度h的值;②中,只要给定了年份(1979~2001)的任意一个值,就唯一地确定了南极上空臭氧层空洞面积;③中,只要给定了年份(1991~2001)的任意一个值,就唯一地确定了我国城镇居民恩格尔系数.即一个变量每取一个确定的值,另一个变量也相应地唯一确定一个值.这时,我们把后者叫前者的函数.
一般地,设集合A是一个非空的实数集,对A内任意实数x,按照确定的对应法则f,都有唯一的实数值y与它对应,则这种对应关系叫做集合A上的一个函数.
好,现在根据函数的定义,判断下列给出的对应法则,是否是实数集R到R的一个函数:
生:……
师:好,同学们学会了根据函数的概念判断一个对应法则给出的对应关系是否确定一个函数.现在请大家举出三个函数的实例.
……
评析 案例中,对函数概念的教学不只是让学生死记硬背函数概念的定义,也不仅仅关注对函数表达式、定义域、值域的讨论,而是通过选取具体事例,引导学生经历对函数概念的实际背景的感知与抽象概括的过程,并在概念的抽象概括过程中合理设置问题情景,使学生体会函数所反映的实际事物的变化规律,经历函数概念的抽象概括过程,同时,通过让学生自己举出函数的实例,辨别真假例子,较好地对函数概念实施“过程性教学”,不但使学生较为深刻地理解函数概念的内涵,有效地促进学生对函数概念本质的理解,而且也从中学会了抽象概括的思想方法.
3 巩固——忌听倡做,实践反思
认知建构学认为,学生是学习的主体.对于数学学习而言,除了学生本人,任何人都无法代替.学生对数学概念的巩固,并不是简单地依赖教师重点强调、反复提醒所能及的,而是学生通过自身对概念的实践运用中加以反思而建构的.相对于显性的知识技能而言,内隐的数学经验的积累、数学方法的习得、数学思想的聚成,都离不开学生的亲自“做”.因此,在数学概念的巩固练习中,仅让学生听老师的指令机械训练是远远不够的,而应忌听倡做,放手让学生在做中积累经验,反思调整,进而深化巩固数学概念.
案例3 “函数的零点”的教学片断.
在学生得出,若函数y=f(x)在区间[a,b]上存在零点,必须满足“连续”和“异号”,两个条件后,教师提出问题:如果这两个条件即“连续”和“异号”,现有一个或两个条件不成立,那么函数还是否存在零点?
学生经过画图象,举反例,反复验证,他们发现函数可能有零点,一些学生还主动上黑板画出了图象(如图1~3.图1是不满足“异号”,图2是不满足“连续”,图3是两个条件都不满足).
同时,学生还发现也可能不存在零点,并举出反例画出图象,恕不赘述.大家感受到“连续”和“异号”这两个条件是函数在闭区间内有零点的充分条件.接着教师提出问题:如果函数y=f(x)在区间[a,b]上有零点,那么一定只有一个吗?
学生们纷纷表示“不一定”,并有几个学生上黑板画出了(图4~6)图象.
教师再提出问题:如果有且只有一个零点的话,还需要满足什么条件吗?
学生经过讨论,最后得到要满足3个(充分)条件:(1)函数y=f(x)的图象在区间[a,b]上连续;(2)f(a)f(b)<0;(3)函数y=f(x)在区间[a,b]上单调.
评析 案例中,在学生得出,若函数y=f(x)在区间[a,b]上存在零点,必须满足“连续”和“异号”,两个条件后,教师通过“如果这两个条件即‘连续和‘异号,现有一个或两个条件不成立,那么函数还是否存在零点?”、“如果函数y=f(x)在区间[a,b]上有零点,那么一定只有一个吗?”、“如果有且只有一个零点的话,还需要满足什么条件吗?”的引导,不仅使学生举出了正例,而且也让学生举出了反例.这样,从概念的形成(具体)到明确概念(一般),再到举出实例(具体)形成一个完整的概念认知过程,有利于学生理解概念,防止死记硬背.
当然,“做”数学不仅要重视由因及果的数学结论的运用,还要重视由果探因的数学背景探究.因此,在概念的巩固练习中,不仅要让学生参与解题,还要重视让学生参与构题.
总之,学生总是基于深刻的数学体验而建构的.在教学中,教师要从帮助学生积累数学经验入手,倡导深入感知,渐进抽象,实践巩固,让学生在深度体验中深刻建构数学概念.
作者简介 赵绪昌,男,1963年生,主任,四川宣汉人, 中学特级教师,四川省学术和技术带头人,苏步青数学教育奖和国务院政府特殊津贴获得者,主要从事中学数学教学研究和中小学教育科学研究.
