破解总复习课核心问题设计的“两板斧”

吴兴元

很多一线教师反映：数学复习课难上，六年级的毕业总复习课更难上！细细思量，原因是多方面的。从学生角度思考，总复习内容涵盖了小学数学的全部概念、性质、公式和法则，要理清知识间的联系与区别，并且能够综合运用，这不是简单的事；从教师角度观察，总复习课不同于新授课和练习课，如果只按教材编排组织复习，容易把复习课上成习题操练课，置学生于题海中。总复习课如何达成知识与技能、过程与方法、情感态度和价值观的三维目标？笔者以为设计有效的数学核心问题尤为重要。数学核心问题有两层含义：其一是指这个数学核心问题由信息和问题组成（信息也可以由学生补充，问题也可以由学生提出），以文字、数据、表格或图画等形式呈现；其二是指这个数学核心问题是复习课的主要材料，贯穿起整个教学环节。一个好的数学核心问题，应当具有起点低、开放度大、结构简单和容量足的特征。那么，总复习课中如何设计有效的核心问题呢？

一板斧：突出数学知识和方法的逻辑结构

总复习课的数学概念、性质、公式、法则很多。如果一个一个割裂地去教学，往往把握不好复习内容多和教学时间少的矛盾关系，导致增加课时，加重学生学习负担。因此，如果可以设计一个好的核心问题，将重要的数学知识和方法整合起来，让学生充分经历求知的复习过程，就可以达到事半功倍的复习效果。

1.抓住数学概念之间的内在联系

以数的概念复习为例，因为数的认识发展史和人们从事的生活劳动关系密切，教材在编写时遵循了小学生的认知规律和“自然数、整数、分数、小数……”的数系扩展顺序。因此，“数的认识”总复习可以紧紧抓住数的概念之间的紧密联系进行教学。如“数的认识总复习”不妨这样设计核心问题：

请你读读下面这组数：2，1.2，328，2944.43， -2 ，2/5

（1）说说它们表示什么意思？

（2）你能把这些数表示在数轴上吗？如果有的数无法直接表示，你还有什么好办法？

（3）这些数字中的“2”表示的意思一样吗？

（4）看到2/5所表示的这个点，你还能想到哪些数呢？

这样的问题设计，引导学生理清了正负数、整数、分数、百分数和小数之间的关系，梳理了数的概念的知识网络。看似很普通，却比带着学生孤立地回忆、分类和解释这些数来得更有价值。

2.抓住图形特征之间的变化联系

小学数学教材体系中，对平面图形的学习不外乎从图形的边和角两个维度进行研究和描述，就单个图形而言，学生一般比较容易掌握其基本特征，但是要求学生来表达不同图形之间的关系时，往往会分不清楚。很多学生不能从边的长短变化来系统认识三角形、长方形、平行四边形和梯形，其实这些图形都可以从动态的视角相互联系。如“平面图形总复习”不妨这样设计核心问题：

请你回忆一下，我们学习过哪些平面图形？

（1）根据学生回答，逐一呈现， 它们各有哪些特征？

（2）三角形能变成平行四边形吗？其他图形之间能互相变一变吗？

（3）利用几何画板让图形动起来，想象和观察它们之间的变化。

通过“几何画板”多媒体技术，让静态的图形动起来，实现多种平面图形的动态转化，是比较具有思维含量的一种方法。在课件演示过程中，教师引导学生先行想象，模拟变化，再辅之直观变化过程，不但达到复习了各种平面图形的特征这一知识和技能的显性目标，也达成了发展空间观念的隐性目标。

3.抓住算理之间的紧密联系

计算教学是小学数学教学的重要组成部分，包含了整数、分数、小数及四则混合计算。以加法计算为例：虽然算法各异，但算理一致，相同的计数单位才能直接相加。如果只重视让学生会算，把增加题量巩固算法作为单一的复习目标，这种做法是不正确的。计算教学的总复习要重视复习怎么算，还要重视复习为什么这么算。如“四则运算总复习”不妨这样设计核心问题：下面的计算正确吗？

157+3 = 160 15.7+3 = 16

1/7+1/3 = 2/10 0.7+2/5 = 1.1

（1）判读：说出错题错在哪里？错题如何改正？

（2）观察：虽然每道题的数据不同，但是这四道题在计算上有共同点吗？

教学中，学生判断、说理、改正和归纳，不过花了五六分钟时间。但这样设计问题，要求学生会算法明算理，实现算理算法互相支撑，使学生达到知其然并知其所以然的目标。

二板斧：紧扣学生的困惑和错误

学生在总复习时最容易遇到的困惑之处在哪里？学生平时作业和测验的典型错误有哪些？有效的核心问题设计需要改变以教材为本和以教师为主的思考方式，要向以学定教、顺学而导的教学理念和教学方式转型。设计时要充分预设学生学习中碰到的各种可能和各种错误，确保每个环节的教学都能贴着学生的思维进行。

1.抓住最易混淆的知识点

小学数学总复习涉及“数与代数、图形与几何、统计与概率和综合与实践”领域的上百个概念、几十个公式，学生要一一掌握并能串联成网状结构是不容易的。特别是面对一些比较抽象的数学概念，更是难以分辨。如分数的意义，它既可以表示具体的数量，又可以表示两种量的关系，学生常常犯迷糊。我们不妨这样设计核心问题：

想一想，填一填：把3千克糖平均分给4个小朋友，每人分到了这些糖的（ ），每人分到（ ）千克。

（1）说说你的答案，重点呈现两种答案：3/4，1/4和1/4，3/4。

（2）说出你的理由，可以通过画图来说明。

分数该怎样定义？一般有份数定义、商定义、比定义和公理化定义。在这个核心问题中，充分考虑到分数份数定义和商定义的结合，引导学生进一步复习，当用份数定义时，不管这个整体具体表示多少量，都看成了“1”。当需要求出这个分数所表示的具体数量时，可以通过除法计算，当然也可以通过分数乘法来解决。这样就把分数所表示的两种含义辨别清楚了。

2.抓住学生的典型错误

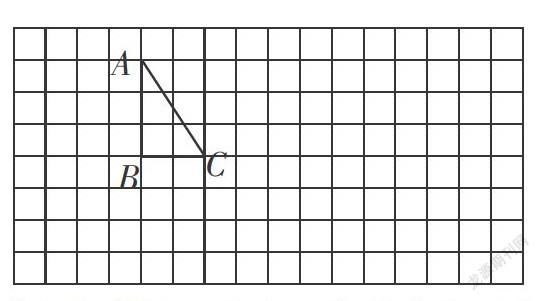
来自于学生练习和测试中的典型错误是宝贵的教学资源，这已成为共识。针对错误设计相应的问题，着力帮助学生找到错因，可以提高复习效率。例如，在复习“图形与变换”内容前，通过教学前测，发现学生在对格子图中的三角形进行图形变换时，画轴对称图形的正确率是100%，画平移图形的正确率是94.7%，画出放大（缩小）图形的正确率是94.7%，而画出三角形绕直角顶点顺时针旋转90°的正确率只有52.6%。由此可见，在复习四种图形变换的基本特征基础上，要加强图形旋转的复习。因此，“图形与变换”的总复习不妨这样设计核心问题：

请你利用三角形ABC，选择一种或几种图形变换方式，设计出你喜欢的图形。

（1）学生独立画图。

（2）交流用一种变换方式的作品。

（3）分享运用两种及以上变换方式设计图形的学生作品。

在交流过程中教师要注意，当学生作品中出现旋转变换时，要求学生说说详细的变化过程。复习是一个“温故知新”的过程，拿学生的主要错误作为设计问题的原材料，可以做到查漏补缺。

3.抓住学生的最薄弱处

数学教学的目标之一，就是要培养学生运用数学知识解决简单的数学问题（包括生活实际问题）。而现实是，很多学生能正确熟练解答基本数量关系的问题，但是遇到数量关系比较复杂的问题时，往往找不到解决问题的具体方法。这其中，分数（百分数）应用是小学阶段解决问题的难点之一，是学生在解决问题系列中最薄弱的环节。针对这种情况，“分数（百分数）解决问题”总复习不妨这样设计核心问题：

已经知道A巧克力和B巧克力的价钱关系中有一个分数1/5。你猜猜它们的价格存在怎样的关系？根据学生回答板书：

①A的价格是B的1/5，②B的价格是A的1/5，③A的价格比B贵1/5，④B的价格比A贵1/5， ⑤A的价格比B便宜1/5，⑥B的价格比A便宜1/5。

（1）已知A巧克力售价30元，你能分别根据①～⑥计算B巧克力的价钱吗？

（2）交流思路。追问：你还能用别的方法解决这些问题吗？

通过以上问题的设计，学生对分数（百分数）问题的结构、分数乘除法之间的关系有了更清晰的认识，进一步沟通了分数解决问题、比例解决问题、运用归一和归总问题三者之间关系，达到了提升综合解决问题能力的教学目标。