初始值对细胞神经网络混沌特性的影响

朱艳平（信阳农林学院　信息工程学院，河南　信阳　464000）



初始值对细胞神经网络混沌特性的影响

朱艳平
（信阳农林学院信息工程学院，河南信阳464000）

摘要：为了能使细胞神经网络系统产生混沌吸引子和混沌信号，以便于将其作为密钥源应用于加密系统中，以四维CNN、五维CNN和六维CNN为例，对细胞神经网络的初始值进行研究.仿真实验得出能够产生混沌特性的初始值取值规律，这一结果将有助于细胞神经网络在加密领域中的应用研究.

关键词：细胞神经网络；初始值；混沌特性；取值规律；加密

细胞神经网络是Chua和Yang在1988年首次提出的，简称为CNN[1-2].CNN是一个局部互联网络，具有复杂的混沌动力学特性，同时又具有实时、高速、并行处理信号，易于超大规模集成电路实现的优点，被广泛应用于加密系统中[3].文献[4-6]分别将CNN系统用于彩色数字水印加密、语音加密和图像加密系统中，均取得了良好的加密效果.

细胞神经网络用于加密的前提条件是，该系统能够产生混沌吸引子和混沌信号.对于已经构造的CNN混沌系统数学模型，初始值的取值不同，将直接影响其混沌吸引子的产生与否.本文分析了初始值对细胞神经网络混沌特性的影响，通过仿真实验，得出能够产生混沌信号的CNN初始值的取值规律.这对细胞神经网络在加密领域的应用，具有一定的理论意义和现实意义.

1　细胞神经网络数学模型

细胞神经网络是受Hopfield神经网络和细胞自动机的影响，而提出的一种人工神经网络[7].对于全互连n阶细胞神经网络的数学模型，其动力学方程如式(1)所示[8]：

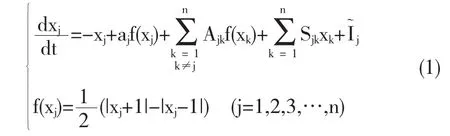
其中j为细胞记号，aj、Ajk、Sjk和I軇j为系统参数，xj为状态变量，f(xj)为细胞对应的分段线性输出函数.若n的取值为4，S11、S23和S33的取值为1，S13和S14的取值为-1，S22的取值为3，S31的取值为12，S32的取值为-13，S41的取值为96，S44的取值为-89，a4的取值为198，其余参数的取值均为0.则四维CNN系统如式(2)所示：

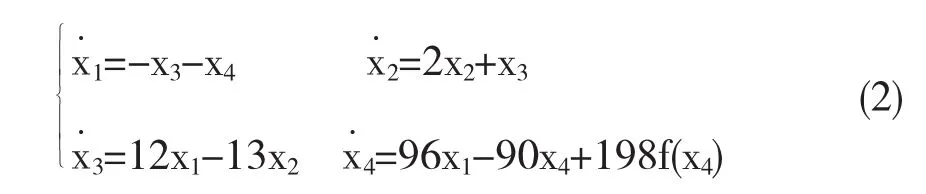
若n的取值为5，S11、S23和S33的取值为1，S13、S14、S45和S55的取值为-1，S22的取值为3，S31的取值为11，S32的取值为-12，S41的取值为92，S44的取值为-94，S53的取值为15，a4的取值为202，其余参数的取值均为0.则五维CNN系统如式(3)所示：

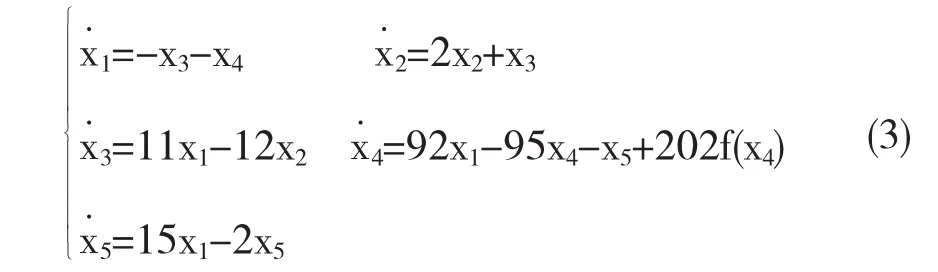
若n的取值为6，S11、S23、S33和S51的取值为1，S22的取值为3，S31的取值为14，S32的取值为-14，S41和S62的取值为100，S44的取值为-99，S52的取值为18，S65的取值为4，S66的取值为-3，a4的取值为200，其余参数的取值均为0.则六维CNN系统如式(4)所示：

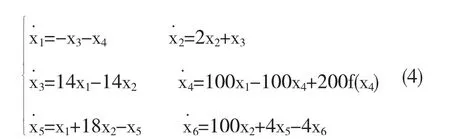
2　初始值对CNN系统混沌动力学行为的影响

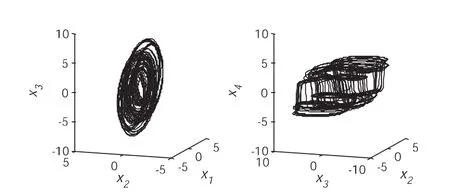
图1　四维CNN系统部分超混沌吸引子

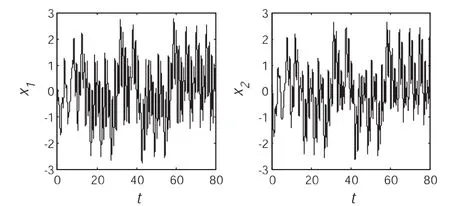
图2　四维CNN系统部分超混沌信号

对于式(2)的四维CNN系统，若初始值x1(0)的取值为0.1，其它四个初始值的取值均为0.2，则该系统的相空间图如图1所示，这里只给出了x1、x2和x3序列所产生的相轨迹，以及x2、x3和x4序列所产生的相轨迹.该系统所产生的部分信号如图2所示，这里只给出了x1和x2的信号，x3和x4的信号与此类似.

从图1和图2可以看出，当初始值的取值为0.1、0.2、0.2和0.2时，该四维CNN系统x1、x2和x3序列能够产生超混沌吸引子，x2、x3和x4序列也能够产生超混沌吸引子.另外该系统产生的x1和x2的信号是超混沌信号，该系统为超混沌系统，可以用作加密系统的密钥源.

若该四维CNN系统的四个初始值取值均为2，则图3给出了x1、x2和x3序列所产生的相轨迹，以及x2、x3和x4序列所产生的相轨迹.图4给出了该系统所产生的x1和x2信号，x3和x4的信号与此类似.

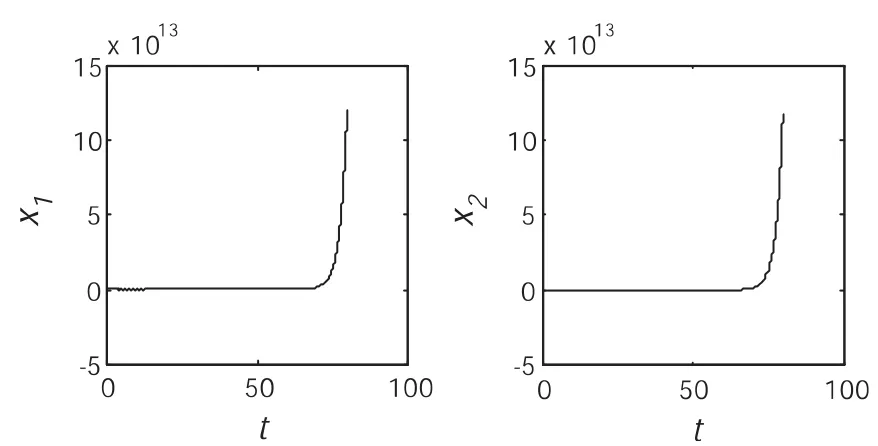
图4　四维CNN系统未能产生超混沌信号

从图3和图4可以看出，当初始值的取值均为2时，序列x1、x2和x3不能产生混沌吸引子，序列x2、x3和x4也不能产生混沌吸引子，x1和x2也不是混沌信号.该四维CNN系统不能够产生超混沌吸引子和超混沌信号，故该系统不是混沌系统.

从图1、图2、图3和图4可以看出，对于同一个四维CNN系统，只因初始值的取值不同，将直接影响该系统能否产生混沌吸引子和混沌信号.若计算精度取小数点后的三位数字，经过仿真实验证明，该四维CNN系统的初始值对其混沌特性的影响如下：

(1)四个初始值不能全部为0，若全部为0，则该系统不能产生混沌吸引子和混沌信号，不具备混沌特性；

(2)当x1(0)∈(-3.259,3.259)且x1(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x2(0)∈(-2.991,2.991)且x2(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x3(0)∈(-10.099,10.099)且x3(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x4(0)∈(-273.055, 273.055)且x4(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性.

(3)当四个初始值取值相同，且均不为0，取值在如下区间内(-1.853,1.853)，则该系统具备混沌特性.

式(3)的五维CNN系统的初始值对其混沌特性的影响如下：

(1)五个初始值不能全部为0，若全部为0，则该系统不具备混沌特性；

(2)当x1(0)∈(-3.203,3.203)且x1(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x2(0)∈(-3.033,3.033)且x2(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x3(0)∈(-9.599,9.599)且x3(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x4(0)∈(-283.750,284.750)且x4(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性.当x5(0)∈(-247.749, 247.749)且x5(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性.

(3)当五个初始值取值相同，且均不为0，取值在如下区间内(-1.839,1.839)，则该系统具备混沌特性.

式(4)的六维CNN系统的初始值对其混沌特性的影响如下：

(1)六个初始值不能全部为0，若全部为0，则该系统不具备混沌特性；

(2)当x1(0)∈(-2.700,2.700)且x1(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x2(0)∈(-2.596,2.596)且x2(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x3(0)∈(-9.387,9.387)且x3(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性；当x4(0)∈(-251.150, 251.150)且x4(0)≠0，而其余的初始值取值均为0时，该系统具备混沌特性.当x1(0)、x2(0)、x3(0)、x4(0)和x6(0)的取值都为0，x5(0)无论取任何值，该系统都不具备混沌特性；当x1(0)、x2(0)、x3(0)、x4(0)和x5(0)的取值都为0，x6(0)无论取任何值，该系统都不具备混沌特性.

(3)当六个初始值取值相同，且均不为0，取值在如下区间内(-1.540,1.540)，则该系统具备混沌特性.

从上面的实验数据可知，当CNN系统的初始值均为0时，该CNN系统不具备混沌特性；当初始值有一个不为0，其余均为0时，不为0的这个初始值取值应满足一定的区间范围，否则该系统不具备混沌特性；当初始值取值都相同且不为0时，取值范围也必须满足一定的区间范围，否则该系统不具备混沌特性.

3　结束语

本文对四维CNN系统、五维CNN系统和六维CNN系统的初始值进行了分析研究，得出初始值对CNN系统混沌特性的影响规律.该研究结果，有助于CNN超混沌系统的构造，并将其作为密钥源应用于加密系统中.目前已有文献将其它混沌系统生成的混沌值作为CNN系统的初始值，再生成CNN超混沌序列用于加密.若其它混沌系统生成的混沌值不满足上述规律，将其作为CNN系统的初始值，是不能够产生混沌序列的.因此该研究结果也有助于加密算法的研究.

参考文献：

〔1〕Changjin Xu, Yusen Wu. Anti-periodic solutions for high -order cellular neural networks with mixed delays and impulses [J]. Advances in Difference Equations, 2015,2015(1):1-14.

〔2〕Liqun Zhou. Global asymptotic stability of cellular neural networks with proportional delays [J].Nonlinear Dynamics, 2014,77(1-2): 41-47.

〔3〕张小红,汪佳.异构细胞神经网络与超混沌系统的同步研究[J].计算机工程与设计,2013,34(3): 1034-1038.

〔4〕赵国敏，李国东，朱文辉.基于DCT和CNN混沌系统的彩色数字水印加密新算法[J].四川理工学院学报(自然科学版),2014,27(5):58-63.

〔5〕朱艳平,闵洁.基于CNN超混沌序列的语音加密方案研究[J].廊坊师范学院学报（自然科学版）,2011,11(2):31～32,37.

〔6〕董虎胜,陆萍,马小虎.基于CNN超混沌系统与扩展ZigZag的图像加密算法[J].计算机应用与软件,2013,30(5):132-136.

〔7〕韩琦.神经网络的稳定性及其在联想记忆中的应用研究[D].重庆:重庆大学,2012.

〔8〕Shukai Duan, Xiaofang Hu, Lidan Wang, et al. Hybrid memristor/RTD structure -based cellular neural networks with applications in image processing [J].Neural Computing and Applications, 2014,25(2):291-296.

基金项目:河南省教育厅高等学校重点科研项目（15A520095，教科技〔2015〕95号）资助.

收稿日期：2015-11-25

中图分类号：TP183

文献标识码：A

文章编号：1673-260X（2016）01-0038-03