Banach空间中线性算子的Drazin广义逆

林梅羽（莆田学院　基础教育学院，福建　莆田　351100）



Banach空间中线性算子的Drazin广义逆

林梅羽
（莆田学院基础教育学院，福建莆田351100）

摘要：通过建立Banach空间中三逆序法的广义Drazin逆，给出Banach空间上2×2有界线性算子矩阵分块的广义Drazin逆的一些表达形式.

关键词：Banach空间；三逆序法；Drazin逆；分块矩阵

1　引言

1958年，Drazin M P[1]在代数半群和结合还上定义了一种伪逆，即为后来被大家广泛称为D的Drazin广义逆.后来，Drazin M P又对方阵的情形对Drazin逆做了深入的研究工作.1975年，Campbell和Meyer Jr C D对矩阵的Drazin广义逆的连续性做了大量的研究并得出一系列的结论[2].从此以后，众多学者们开始研究矩阵的Drazin广义逆，于是使得矩阵的Drazin广义逆得到了空前的发展.

关于Banach空间中线性算子的Drazin广义逆的研究工作是上世纪90年代前后开始的研究领域.早期可追溯到1981年，乔三正为Banach空间中有界线性算子a引入了Drazin广义逆ad的定义，并给出了Drazin广义逆的表示[3].

1985年，蔡东汉在乔三正研究成果的基础上继续研究Banach空间中有界线性算子的Drazin广义逆这一研究工作，同时给出了Banach空间中有界线性算子a的Drazin广义逆ad的另外一种新的表达形式[3].

2000年，魏伊敏也研究了Banach空间中有界线性算子的Drazin广义逆，同时给出了不同于上述两种情形的表达式[3].

通过建立Banach空间中三逆序法的广义Drazin逆，给出Banach空间上2×2有界线性算子矩阵分块的广义Drazin逆的一些表达形式.该研究中虽然添加了比较强的条件，但是这里所采取的方法确实新颖的，该方法在别的参考文献中还没有出现，而且利用该方法确实也可以得出了很好的一些结论，相信该方法的引入和几个重要的结论对今后其他学者们对矩阵的Drazin广义逆会有更好的启发.

2　预备知识

设A是有幺元的B代数，σ(a)和r(a)分别为a的谱和谱半径，其中a∈A.记A-1为B代数A的可逆元素集，A0为B代数A的幂零元素集，A00为B代数A的拟幂零元素集.

如果存在元素b∈A满足aba=a，则称元素a∈A是正则的，同时我们把元素b∈A称为元素a∈A的内逆.记元素a∈A的所有内逆集为a{1}，且B代数A的所有正则元素集为A+.

设a∈A，则a∈A的广义Drazin逆是唯一的，记为ad∈A，且满足

adaad=ad，aad=ada，a-a2ad∈A0设Ad为B代数A的所有的广义Drazin可逆元素，如果a∈Ad，那么有关集合{0}的谱幂零aπ=1-aad，并且如果ac=ca，那么必有adc=cad，其中c ∈A.

引理2.1设a∈Ad，a∈A0.如果ab=0，那么a+b∈Ad，且

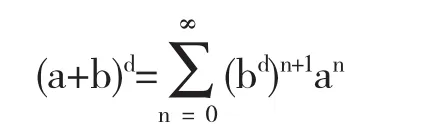
证明详细参见参考文献[4].

引理2.2设b∈Ad，a∈A0.如果ba=0，那么a+b∈Ad，且

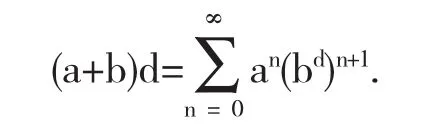
证明详细参见参考文献[4].

如果a∈A，p=p2∈A且是幂零的，那么a∈A具有如下分块矩阵表达形式：

其中，a11=pap，a12=pa(1-p)，a21=(1-p)ap，a22(1-p)a (1-p).

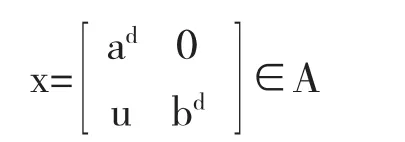
证明参见参考文献[5,6,7].

接下来，将利用反序法讨论元素乘积abc的广义Drazin逆，其中，a和c是Banach空间中的可逆元素，而b是Banach空间中的广义Drazin可逆元素.下面首先给出反序法(abc)-1=c-1b-1a-1的一个充分必要条件，然后利用该反序法给出Banach空间中的分块矩阵的广义Drazin逆的一种新的公式，且该公式具有更加的一般性.

3　主要结论

首先，研究了三个元素乘积的广义Drazin逆的反序法，该方法可以帮助建立Banach空间中的分块矩阵的广义Drazin逆的充分条件.

定理3.1设a∈A-1，c∈A-1且b∈Ad.如果cab=bca，那么abc∈Ad且(abc)d=c-1bda-1.证明设x=abc且y=c-1b-1a-1.显然

yxy=c-1bdbbda-1=y

因为b与ca且可交换，所以广义Drazin逆bd与ca也可交换.

因此cabbd=bdbca，从而

xy=abbda-1=c-1bdbc=yx

由于x-xyx=abc-abbdbc=abbπ且cabbπ=bπbca，因此我们得到

0≤r(x-xyx)=r(abbπc)=r(bbπca)≤r(bbπ)r(ac)=0

于是r(x-xyx)=0，从而x-xyx∈A0.因此

x∈Ad且xd=y

利用同样的方法，还可以得出下面的推论3.1[8,9].

推论3.1如果a,c∈A-1且b∈A00.那么cabb00=b00bca的充分必要条件为

abc∈A00且(abc)00=c-1b00a-1.接下来，根据Banach空间中三逆序法证明下面的定理3.2.

定理3.2设a,c∈A-1且b∈A.假设ab∈Ad， bc∈A+且(bc)(1)∈(bc){1}.则

如果cab=abc，那么ab(ab)d=(bc)(1)bc的充分必要条件为

abc∈Ad且(abc)d=(bc)(1)b(ab)d证明设x=abc且y=(bc)(1)b(ab)d.则有

yxy=(bc)(1)b(ab)dabcc-1(ab)d=y

因为c与ab且可交换，所以(ab)d与c也可交换，从而得出

r(x-xyx)=r((ab)πabc)≤r((ab)πab)r(c)=0因此x-xyx∈A0，从而x∈Ad且xd=y与xy=yx等价.

因为xy=ab(ab)d且yx=(bc)(1)bc，从而可得xy=yx的充分必要条件为

ab(ab)d=(bc)(1)bc.利用定理3.2的证明方法很容易得到下面的相应的推论3.2[10,11].

推论3.2设a,c∈A-1且b∈A.假设ab∈A00，bc∈A+且(bc)(1)∈(bc){1}.则ab(ab)+=(bc)(1)bc的充分必要条件为

abc∈A+且(abc)+=(bc)(1)b(ab)+

设

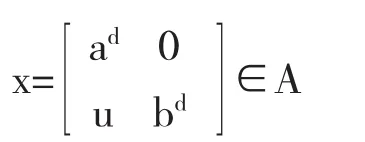
其对应的幂元p∈A且a∈(pAp)d.

设广义的Schur补为s=d-cadb∈((1-p)A(1-p))d.

利用定理3.1中的逆序法则可以得到广义Drazin xd几个具体表达式（详见下面几个重要的定理），该表达式均以ad与sd的形式给出的.

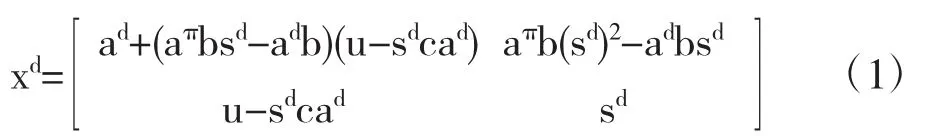
证明设x=x1x2x3，其中

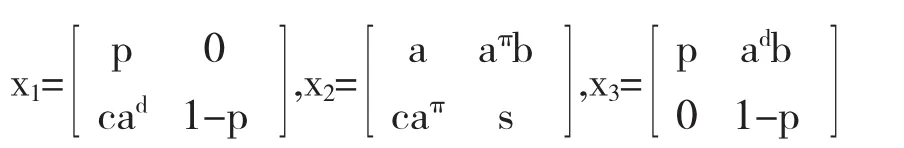
显然x1,x3∈A-1,且

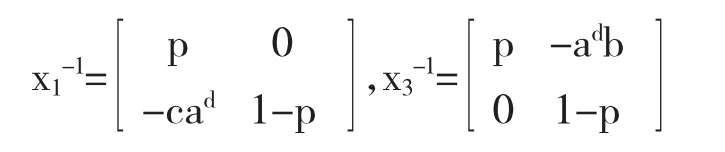
下面证明x2∈Ad.设x2=y+z其中

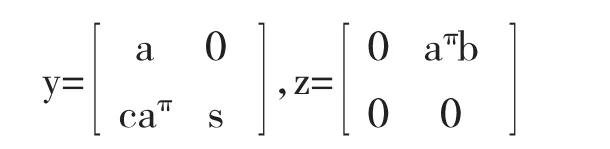
由于z2=0,aaπb=0且caπb=0,从而z∈A0且yz=0.利用定理2.1得y∈Ad且

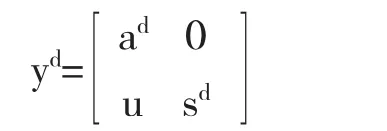
利用引理2.1得x2∈Ad且

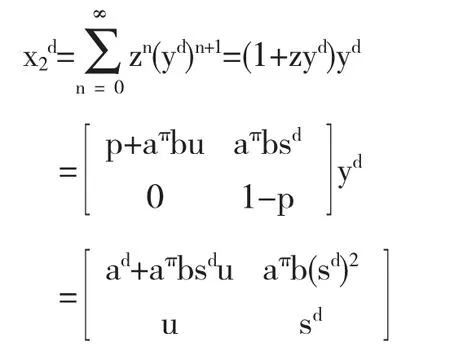
由于abc=bca，ca2=sca且abs=a2b，从而adbc=bcad，caad=scad且adbs=aadb

由于

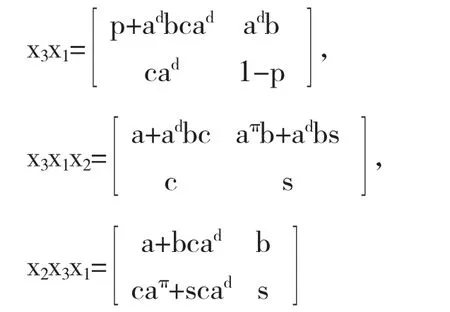
从而可得x3x1x2=x2x3x1.

所以利用定理3.1和上述（1）式可得

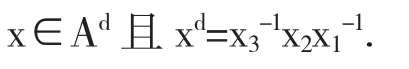
aπbcaπ=0，aπbs=0，abc=bca，ca2=sca且abs=s2b 则x∈Ad且

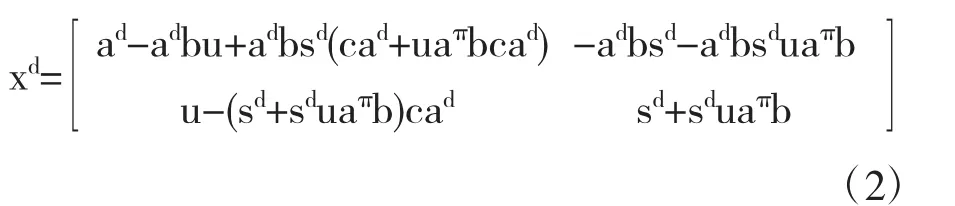
证明类似定理3.3.

根据上述定理3.3和定理3.4可得如下推论3.3.

abc=bca，ca2=sca且abs=a2b

则

（1）如果aπb=0，则x∈ad且

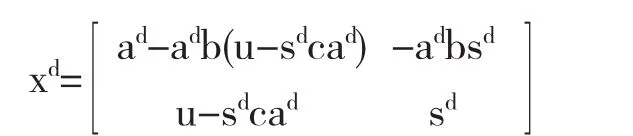
（2）如果aπb=0且caπ=0，则x∈Ad且

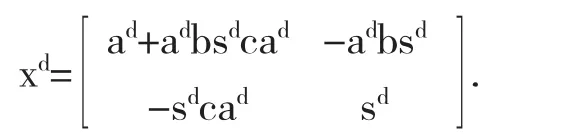
参考文献：

〔1〕Koliha J J. A generalized Drazin inverse [J]. Glasgow Math J,1996,38:367-381.

〔2〕Djordjevic D S, Wei Yimin. Additive results for the generalized Drazin invers [J]. J Austral Math Soc, 2002,73(1):115-125.

〔3〕王玉文,李国强.Banach空间中线性算子的Drazin广义逆的表示[J].应用数学学报，2007,30(2)：304-311.

〔4〕Campbell, S L , Meyer, C D. Generalized Inverses of Linear Transformations [M]. Pitman, London,1979.

〔5〕Djordjevic D S, Rakocevic V. Lecturea on the generalized invers[M]. Serbia:Faculty of sciences and Mathematics, University of Nis, 2008.

〔6〕Deng Chunyuan, Wei Yimin. New additive results foe the generalized Drazin invers [J]. J Math Anal Appl, 2010, 370:313-321.

〔7〕Deng Chunyuan, Wei Yimin. Reprensentation for the generalized Drazin invers of 2X2 block -operator matrix with singular Schur complement [J]. Linear Appl. 2011,435:2766-2783.

〔8〕杨志荣.2X2分块矩阵的Drazin逆[J].江南大学学报：自然科学版，2009,8(6):733-735.

〔9〕庄桂芬.一类分块矩阵的Drazin逆表示[J].江南大学学报：自然科学版，2010,9:107-109.

〔10〕刘晓冀,覃永辉.Banach代数上广义Drazin逆的扰动[J].数学学报,2014，57(1):35-46.

〔11〕刘英,杨晓丹.Banach空间中Drazin逆的新扰动定理[J].数学实践与认识,2011,41 (8):228-232.

收稿日期：2015-10-13

中图分类号：O177

文献标识码：A

文章编号：1673-260X（2016）01-0001-03