总结归纳法在独立院校线性代数教学中的应用
2016-03-21盛夏吉林建筑工程学院城建学院基础部吉林长春130111
盛夏(吉林建筑工程学院城建学院 基础部,吉林 长春 130111)
总结归纳法在独立院校线性代数教学中的应用
盛夏
(吉林建筑工程学院城建学院基础部,吉林长春130111)
摘要:线性代数是工科类院校的一门重要基础课程,本文在独立院校面临的教学趋势下,从实际教学角度出发,探讨了包含教师总结和引导学生总结在内的总结归纳法在此类院校线性代数教学中的重要作用.
关键词:线性代数;总结归纳法;工科类独立院校
1 线性代数教学面临的形势
线性代数作为作为高校数学教学中的一科,教学方法已经被越来越多的探讨,它具有体系性强、知识点多、应用性广、逻辑性抽象性要求高以及计算量大等学科特点[1].而在很多独立性院校中,教师授课又大都面临着课时紧张、课程要求高、学生不重视、学生数学基础相对偏低等等影响着这门学科教学发展的各种因素.
线性代数和同为数学科目的高等数学相比,充分体现了“时间紧,任务重”的教学特点,在40学时甚至更短的时间里,要把行列式、矩阵、线性方程组、向量、二次型等诸多内容向学生讲解透彻还是很困难的.那么,怎样改进教学方式,使其更适合工科类独立院校的教学,就成为了迫切的研究课题.
2 总结归纳法教学的应用
通过与工科专业类教师的探讨,我们发现对于这类独立院校,他们更注重学生在数学学习中计算能力和应用能力的的掌握,而非如数学专业类学生一般进行定理或性质的分析证明.而在实际教学中,我发现我们的学生更容易接受对书中的知识进行适当的总结归纳这种教学方式,这在教学中起到了关键性的作用.
2.1教师总结
2.1.1小总结
前文提到了线性代数的学科特点,决定了其知识点杂乱繁多这一特性,那么在每次课后根据自己的教学特点进行的知识点总结就显得尤其重要了.我们以“行列式的性质”这一小节为例,在多数教材中都是将几条性质及相应推论一一列出,如《线性代数[理工类]》教材[2]中,写到:
性质1行列式与它的转置行列式相等.
性质2行列式某行(列)元素的公因子可以提到行列式符号之外.
推论行列式中某一行(列)为零,则行列式为零.
性质3若行列式的某一行(列)的元素都是两数之和,则行列式可按此行(列)拆成两个行列式之和.
性质4互换行列式中两行(列),行列式变号.
性质5如果行列式中有两行(列)对应元素都相等,则行列式为零.
性质6行列式中两行(列)成比例,则行列式为零.
性质7把行列式的某一行(列)的各元素乘以同一个数加到另一行(列)对应的元素上,行列式值不变.
这对于课堂讲授当然没有问题,其中教师可联系它们的内在特点将讲解顺序适当打乱重整,这样可以帮助理解.但是,这样逐条记并不利于学生记忆及应用,那么我们可以给这些性质进行一个小总结,即
公司以经协商变更劳动合同未达成协议为由向成锐送达了解除劳动合同通知书,与成锐解除劳动合同的行为亦不符合法律规定,因此,二审法院认为,原审法院认定公司上述行为属于违法解除劳动合同,应当向成锐支付违法解除劳动合同赔偿金并无不当。公司的上诉意见与法律规定不符,对其上诉意见不予采纳。

图1 行列式性质总结图
这样,将行列式性质根据不同的用途,分成几大类,非常便于计算应用和背诵记忆.我们还可以讲很多课上的整块内容进行归纳总结,以求达到事半功倍的效果.
1.2章节总结
除了小总结,每当学完一大章我们还应进行章节性的总结以及和前期相关内容的对比.相比起来,如果说小总结是便于学生记忆和计算应用的,那么章节总结就是建立部分知识框架的.例如,“线性方程组”一章中,向量组的线性相关性同方程组解的判定结合,将行列式与秩的判别法融入其中,可以总结如下.
(1)线性相关性(齐次线性方程组):
存在k1,k2,…,km,使得k1α1+k2α2+…+kmαm=0,若k1,k2,…,


(2)线性表示(非齐次线性方程组):
β能否由α1,α2,…,αm,使得k1α1+k2α2+…+kmαm=β,

图2 线性方程组章节总结图
这样,我们就达到了化一章为一图的效果,在这张“图”可以不包含该章节的的所有知识点,毕竟有些知识点与主框架联系并不是那么直接,强行加入反而破坏了整体的结构,使学生更加混乱.但在这张“图”中整体的完整性和关联性必须要保证.
主线总结相比起之前的小总结和章节总结,更加强调对一门课程的整体的把握,以及此门课程的方向性和目的性.我们以Gauss消元法为引,以求解线性方程组为出发点,融入行列式与矩阵的概念与运算,同时结合线性变换引导学生理解特征值、特征向量以及二次型的理论,为学生总结了工科专业类本科线性代数的总体结构图[3],如下
针对不同专业的学生,每名教师所给出的总结或许出发点与主线有一定的区别,但是一个合理的主线总结可以为学生提供学习《线性代数》必要的整体“认识框架”.
2 教师引导学生总结
常言道:“授人以鱼不如授人以渔”.教师总结是必的,而教师引导学生进行独立归纳总结更是必须的,它是帮助学生学习《线性代数》的一大利器.因为大量零散的定理性质或者公式分散在每一章每一节的各个部分,单靠教师的硬性灌输并不能让学生完全“主动”的支配这些内容.所以,学生即使课上听懂了,在课下做题时,仍需要反复的查阅教材,这给他们做题带来了相当大的困难,久而久之,部分学生就会逐渐丧失学习兴趣,这让本来学习气氛就不够浓烈的工科类独立院校显得更加松散.
如果我们能引导学生自行总结一些简单、数量庞大的公式,学生就会在动手过程中达到学习和巩固知识的目的,而且能培养独立思考、综合分析、归纳总结的能力.此外,学生经过一段时间的总结,还会对这些内容产生一定的“感情”,这对他们日后的学习应用会非常有帮助.
例如,在第二章矩阵的学习中,含有大量的运算律,包括:矩阵的加法、数乘、乘法、方幂、转置、矩阵的行列式、逆以及矩阵的伴随等,这些公式分布在整个第二章,特别不利于记忆,而且他们当中的一部分因相似度高而容易混淆.我要求学生将它们誊抄到一起,这样运算律之间的区别与练习一目了然.而后引导学生在做题过程中“查阅”,用法类似于查字典.此外,我还建议学生在公式后面留一部分空白,每当一个公式被“查阅”一次,就给这个公式做个记号,那么到了期末复习时,再重新回看这张纸,就会发现,哪些公式更常用,哪些次之,这对学生的学习复习备考等都有极大的帮助.
引导学生总结的做法可以激发学生学习课程的主动性和积极性,提高学生对该课程的学习兴趣,培养学生对线性代数课程内容的分析、归纳、总结和演绎等基本素质.[4]
3 结语
总结归纳法是一种行之有效的教学方法,在教学中科学合理的应用可以降低教学难度、加深学生对内容的理解、令知识体系一目了然.而要做到这些就必须要保证归纳的完整性、合理性、准确性,并且达到脉络清晰、简明扼要、化繁为简的效果.这样提高学生学习兴趣,增加他们学习信心的同时,又培养学生的思维能力、创新能力,进而提高学生的科学素养,使他们受益终身[5].
参考文献:
〔1〕严萍,漆珍萍,吴斌.工科线性代数的教学策略研究[J].景德镇高专学报,2008,23(2):25-26.
〔2〕肖马成.线性代数(理工类)[M].北京:高等教育出版社, 2011.
〔3〕王瑞,夏爱生,刘艳娜,等.《线性代数(非数学专业)》整体教学的实践与认识[J].大学数学,2011,27(6):11-14.
〔4〕时娟.线性代数教学初探[J].兰州教育学院学报,2003(4): 58-59.
〔5〕王颖,南基洙.线性代数教学中的归纳与演绎方法[J].高等数学研究,2013,16(6):46-48.
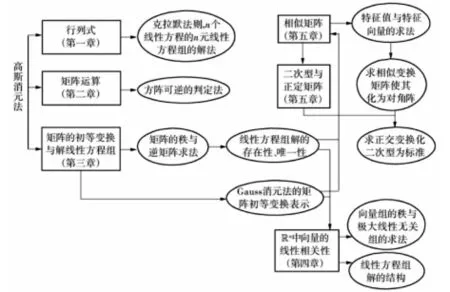
图3 线性代数总体结构图
收稿日期:2015-10-13
中图分类号:O151.2;G642.4
文献标识码:A
文章编号:1673-260X(2016)01-0004-02
