双核铜配合物磁性的理论计算与研究

2016-03-21高晶晶延安大学化学与化工学院陕西省化学反应工程重点实验室陕西延安716000

赤峰学院学报·自然科学版 2016年1期

关键词：磁性

高晶晶,师　磊,唐　龙（延安大学　化学与化工学院，陕西省化学反应工程重点实验室，陕西　延安　716000）

双核铜配合物磁性的理论计算与研究

高晶晶,师磊,唐龙*
（延安大学化学与化工学院，陕西省化学反应工程重点实验室，陕西延安716000）

摘要：本文选取了两种铜(II)配合物[Cu2(l-HCOO)4(PhNHpy)2](1)和[Cu2(pic)2(μ1,3-H2NCO-N-CN)2(H2O)2](2)，配合物1是由羧酸根离子桥联的笼状双核铜结构，配合物2是有机含氮配体桥联的双核铜结构，并对配合物1和2进行了理论计算与研究.本文选择的配合物1和2为双核单元，采用混合密度泛函B3LYP方法，选用6-31G(d)、LanL2DZ和SV/SVP不同的基组，并结合对称性破损态理论计算其磁偶合作用常数J值，对配合物1和2的两个磁中心原子Cu(II)自旋密度进行了分析.结果计算表明配合物1和2的磁偶合作用常数(J)的计算值和实验值相吻合.

关键词：双核Cu(II)配合物；磁性；密度泛函理论

*为通讯作者

近年来，由于分子磁性材料研究领域处于化学、物理、材料、信息和生物等多学科领域的交叉点，所以分子磁性材料的研究已经成为化学学科的前沿领域之一[1-2].随着分子磁性材料的研究与应用，分子磁性材料必将深远地影响着材料科学、配位化学、生命科学和生物医药等各个领域的发展和进步[3].对于双核铜Cu(II)配合物的磁性分子，每个磁中心只有一个未配对电子，研究此双核铜Cu(II)配合物体系在配位化学上具有相当重要和典型的意义[4]，有利于对分子磁交换作用的机理进行深入探讨与研究[5].

基于此，本文选用双核铜配合物分子进行磁性的理论计算与研究，通过理论计算来解释磁性和结构之间的关系，期望能为实验研究提供理论依据，为进一步探索分子磁性材料鉴定基础[6].在研究的双核铜配合物中，我们采用混合密度泛函B3LYP方法来计算磁偶合作用常数，并在考虑对称破损态(BS)下来计算该分子的磁偶合作用常数[7].我们选取了两种的双核铜配合物体系进行分析，羧酸根离子桥联的笼状双核铜体系[Cu2(l-HCOO)4(PhNHpy)2] (1)[8]与氮桥联的双核铜体系[Cu2(pic)2(μ1,3-H2NCO–N–CN)2(H2O)2](2)[9].

1　实验部分

1.1双核铜的理论方法和公式

目前，应用量子化学研究分子磁性材料的理论基础来自于Heisenberg模型[10]，自旋哈密顿算符表示为：H=-2JABSA·SB(1).交换偶合常数可表示为：2J=ES-ET(2)，Es和Et分别为纯单重态与纯三重态的能量.如果考虑破损对称形式，则J可用下式来计算为破损对称态的能量.重叠矫正a2可以根据2a2=〈S赞2〉bs，由期望值BS态S赞2来计算，从而得到公式，进而可求得：考虑三重态，可得到纯三重态的能量：，由(6)式得(7)，再根据(5)和(7)计算得分别计算Ebs与和Ebt与，根据公式，可以求得J值.

1.2计算方法

本文利用Gaussian03量化软件包进行计算的，采用混合密度泛函B3LYP方法，基函数采用6-31G（d）基组，赝势LanL2DZ基组和SV /SVP全电子基组进行计算.

2　结果与讨论

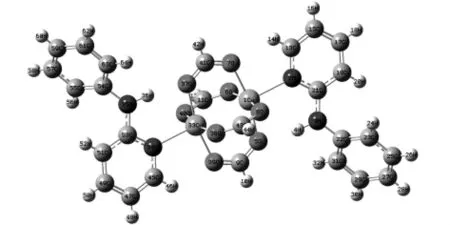
图1　配合物1的结构图

2.1配合物1和2的结构示意图

从文献中我们选取两种配合物：双核笼状铜配合物(1)和有机含氮配体桥联的双核铜配合物(2)的结构示意图如图1和图2.

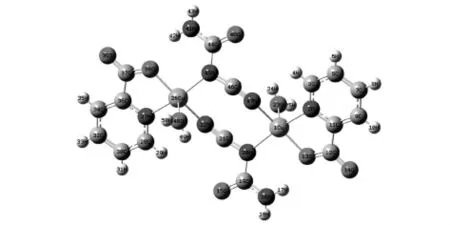
图2　配合物2的结构图

2.2配合物1和2的磁耦合常数计算结果

在实验的基础上，选取晶体结构中双核铜Cu的基本单元，在混合密度泛函B3LYP方法的基础上我们分别选用6-31G（d），LanL2DZ和SV/SVP等三种不同的基组对上述两种配合物1和2进行了理论计算与研究，计算得到其磁耦合常数及实验值的结果如表1和2.

表1　配合物1分子HS态和BS态的能量、S赞2本征值和J值

表2　配合物2分子HS态和BS态的能量、S2本征值和J值

在表1和表2中我们采用三种基组对配合物1计算得到的J值与实验值进行比较，我们发现利用LanL2DZ基组计算的结果最接近实验值，与实验值基本一致.而利用6-31G(d）和SV/SVP基组计算的值与实验值相差较大.也就是说对于双核铜的磁耦合常数计算采用LanL2DZ基组是合理的.选用不同的基组计算我们可以看到配合物1和2中HS态的期望值与理论值2.00非常接近,说明我们所计算的配合物1和2的HS态能量近似为纯三重态能量[11].

2.3配合物1和2的分子自旋密度

在实验的基础上，选用同样的方法和三种不同的基组对上述两种配合物1和2进行了自旋密度分布计算与研究，计算结果见表3和4.

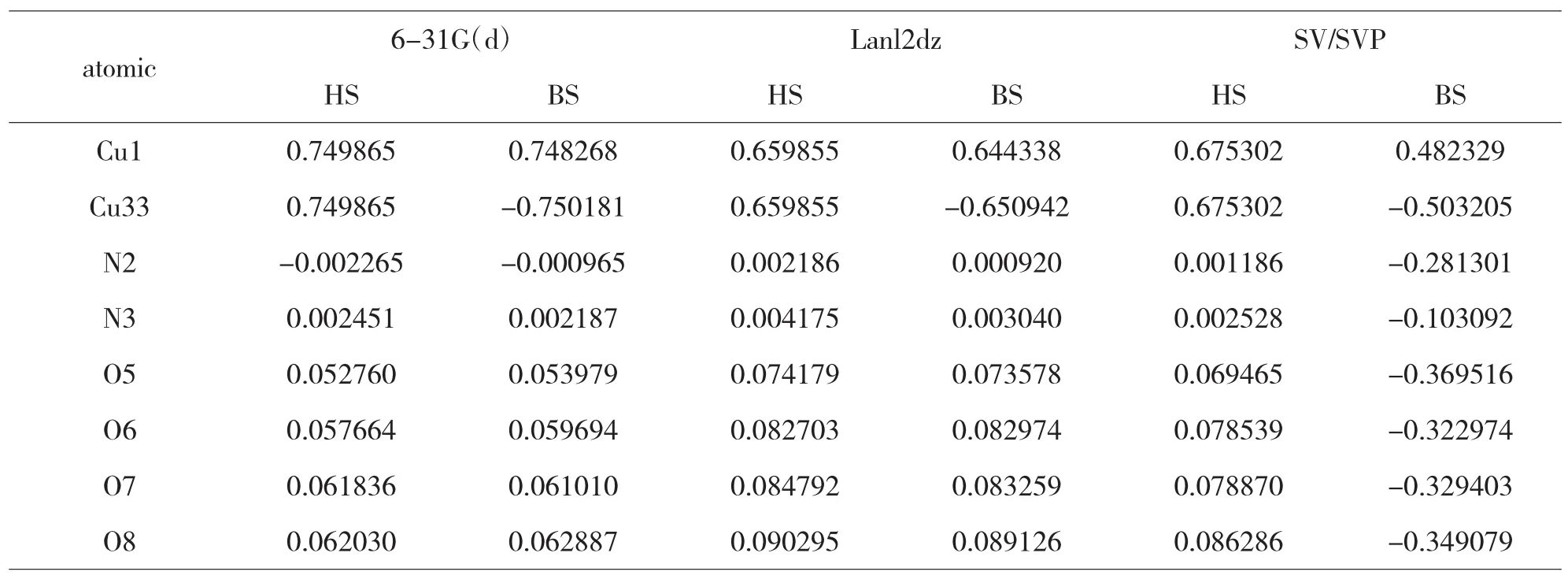
表3　配合物1分子的自旋密度分布

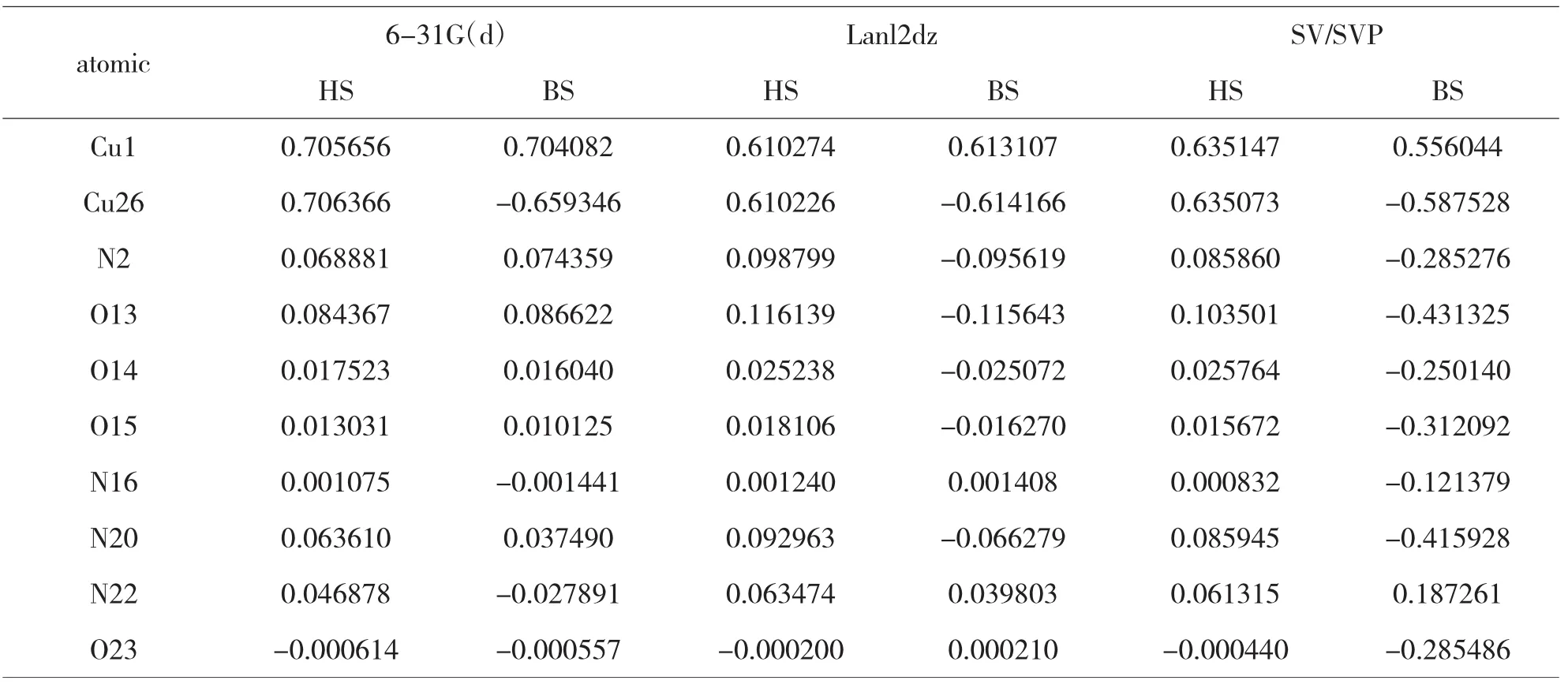
表4　配合物2分子的自旋密度分布

由表3和表4的自旋密度数据可知，对于配合物1和2中，采用三种基组计算：高自旋态(HS)下，两个磁中心原子Cu(II)上的自旋密度值表明有部分自旋电子离域.与磁中心原子Cu(II)直接配位的原子的自旋密度符号与Cu(II)相同，都为正值，表明磁中心的自旋电子离域直接配位的配体原子上，即自旋离域机理.对称性破损态(BS)下，两个磁中心原子Cu(II)上的自旋密度值同样也有部分自旋电子离域.

3　结论

本文选择的配合物1和2为双核单元，采用混合密度泛函B3LYP方法，选用6-31G(d)、LanL2DZ 和SV/SVP不同的基组，并结合对称性破损态理论计算其磁偶合作用常数J值，并对配合物1和2的两个磁中心原子Cu(II)自旋密度进行了分析.通过计算与分析，采用混合密度泛函理论B3LYP方法选用LanL2DZ基组计算双核铜配合物的磁偶合作用常数J值是一种比较理想的方法，与实验值基本吻合，可以采用理论计算预测双核铜配合物的磁性.

参考文献：

〔1〕卫丽娜.氰根桥联多金属配合物分子磁体的磁性研究[D].广西师范大学,2008.

〔2〕孙友敏.多核及金属一自由基配合物分子磁性的理论研究[D].山东大学,2004.

〔3〕谭永新.双核铜配合物磁学性质的密度泛函理论研究[D].贵州大学,2008.

〔4〕裘著有,韩铁,王文新,等.分子磁性材料的研究进展[J].纳米科技,2006（3）:15-19.

〔5〕张义权.金属配合物分子磁性的理论研究[D].南京师范大学,2003.

〔6〕齐中囡.多核磁耦合体系的理论研究[D].山东大学,2006.

〔7〕王丽丽.多核过渡金属配合物分子磁性的理论研究[D].山东大学,2011.

〔8〕Barquin M, Gonzalez-Garmendia M J, Larrinaga L, Pinilla E, et al. Inorg.Chim.Acta, 2006, 359: 2424-2430.

〔9〕Salah S M, Febee R L, Masahiro M, et al.. Inorg.Chim.Acta, 2009,12:420–425.

〔10〕Heisenberg, W. Theory of ferromagnetism[J]. Z. Phys.1928,49:619.

〔11〕张义权,罗成林,余智,等.无机化学学报,2002 （11）:1147-1150.