先直观感知，再精密验证——“f［f（x）］”型函数问题处理技巧

吉林 林逸凡

先直观感知，再精密验证
——“f［f（x）］”型函数问题处理技巧

吉林 林逸凡

对于函数f（x），若f（x0）＝x0，则称x0为函数f（x）的“不动点”；若f［f（x0）］＝x0，则称x0为函数f（x）的“稳定点”．高考中对不动点和稳定点的性质进行研究讨论的“f［f（x）］”型函数问题，是常见的经典题型．

1．标准答案：思维成品难共鸣

【例题】（浙江大学自主招生）设M＝｛x｜f（x）＝x｝，N＝｛x｜f［f（x）］＝x｝．

（Ⅱ）f（x）为单调递增时，是否有M＝N？并证明．

【答案】（Ⅰ）略．（Ⅱ）M＝N．用反证法证明：

①若f（x0）＞x0，由于f（x）为单调递增函数，所以f［f（x0）］＞f（x0），即x0＞f（x0），矛盾；

②若f（x0）＜x0，由于f（x）为单调递增函数，所以f［f（x0）］＜f（x0），即x0＜f（x0），矛盾．

综合①②可知，f（x0）＝x0，因此x0∈M，与假设矛盾，所以假设不成立，故M＝N．

【评注】对于抽象函数问题，因为没有给出具体的解析式，因此对其性质理解起来本就十分困难．标准答案仅仅是出题人思维活动过后的成果展示，虽然逻辑上滴水不漏，结构上完美无瑕，但正因其过于严丝密合、浑然天成，有时反而有种“无从下口”的感觉，不能体会解题思路的形成过程，难以产生“共鸣”，特别是第二问中，“反证法”的思想是一个最大难点，是很难想到的．

2．思路形成：先出草图再润色

如果f（x0）≠x0，不妨把f（x0）记为y0，则y0＝f（x0），y0≠x0，用y0表示f［f（x0）］＝x0这个条件就成了：f（y0）＝x0．

现在已经有了下列条件：y0＝f（x0）、f（y0）＝x0、y0≠x0、f（x）单调递增．

观察这两个条件：y0＝f（x0）、f（y0）＝x0，发现点（y0，x0）和点（x0，y0）都在函数f（x）的图象上，可以画出草图如图：

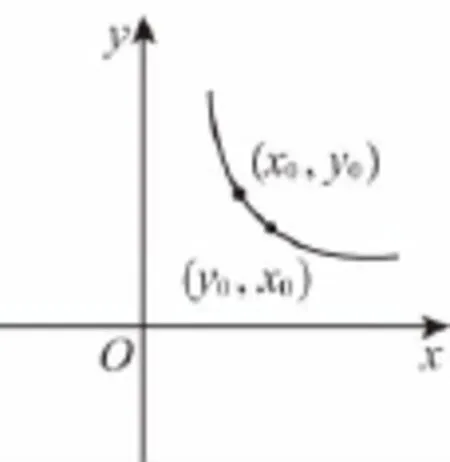
其中点（y0，x0）和点（x0，y0）这两个点应该是关于直线y＝x对称的．

这个函数图象显然不满足题意，因为题中要求函数是单调递增的，这样画不管怎么样肯定有一段区间上单调递减．这是在当y0≠x0时，画出的大致草图，当y0＝x0时，点（y0，x0）和点（x0，y0）重合，缩成了直线y＝x上的一个点，这个时候函数f（x）就可以是在定义域上单调递增的了．

现在就大概明白了单调递增这个条件是怎么回事了，它原来是要求（y0，x0）和（x0，y0）这两个点不会分别出现在直线y＝x的两侧，也就只能重合了．至此已经可以轻松自然地按着这个思路继续完成例题的证明，对这道题的设计思路也有了更为深刻的理解，并且形成一个小结论：对于一个单调递增的函数来说，它的不动点和稳定点应该是完全一样的．

再回过头来看这道题的解题过程，在做这类f［f（x）］型问题时，一般的处理方法是：

令f（x）的一个函数值为y0＝f（x0），然后再把这个函数值y0视为一个新的自变量，代回f（x），再根据实际条件解题．

例如在这道题中，根据f［f（x）］＝x的条件，（y0，x0）和（x0，y0）都在f（x）的图象上．

3．效果验收：牛刀小试露锋芒

“f［f（x）］”型函数是常见题型，接下来通过以下几道变式练习进行进一步的加强和巩固，由于都是选择和填空的小题，证明过程不要求很严密，重点在抓处理这类问题的“感觉”．

A．［1，e］ B．［e－1－1，1］

C．［1，e＋1］ D．［e－1－1，e＋1］

【解析】已知f［f（y0）］＝y0，则y＝f（x）过（f（y0），y0）和（y0，f（y0）），两者若不是同一个点，则关于y＝x对称，又函数是增函数，不可能有这种情况，所以，设g′（ln2）＝3－2ln2＞0，则g（t）是增函数，则a∈［g（0），g（1）］＝［1，e］．

4．触类旁通：思路大同走天下

在掌握基本技巧以后，除了“f［f（x）］”型函数问题，处理类似的“f［g（x）］”型函数问题也不在话下，如变式4．

【变式4】若函数f（x）和g（x）都是定义在实数集R上的函数，且方程x－f［g（x）］＝0有实数解，则g［f（x）］不可能是（ ）

【解析】令y＝g（x），代入条件f［g（x）］＝x中，∴f（y）＝x，∴有g［f（y）］＝g（x）＝y，故方程g［f（x）］＝x有实数解，即系数b，c满足x2＋bx＋c＝x有实数解即可，x2＋（b－1）x＋c＝0，Δ＝（b－1）2－4c≥0，除了B选项，均满足条件．

【反思】对抽象函数的性质探究，不妨先通过“形象但不够严密”的手段，从题设条件（出发点）和结论（目的地）入手，通过对自己发起一系列低起点、多步骤的问题串，对解题形成一个大致思路，再着手解决具体问题，通过不断修饰完善，使解题步骤连贯起来，变得严密．经历“由特殊到一般，再由一般到特殊”的思维过程，对这类型的题目形成整体的把控能力，举一反三触类旁通，达到知识与方法的迁移，做到举一反三、触类旁通．手中有粮，心中不慌，面对难题，不再犯怵．

（作者单位：吉林省长春市吉大附中实验学校高中部）