圆锥曲线中的易错点分析
2016-03-18甘肃张自鹤
甘肃 张自鹤
圆锥曲线中的易错点分析
甘肃 张自鹤
圆锥曲线是解析几何的主要内容,在高考试题中分值约占15%,在选择题、填空题中一般考查基础知识,解答题中必有一题,常作为把关题或压轴题,其考查重点是直线与圆锥曲线的位置关系、求曲线方程、最值问题等,着重考查学生的数形结合、等价转化、分类讨论、函数与方程、运算等方面的能力,对学生的思维能力、方法要求高,难度较大,但只要打好基础知识,有意识地防范一些易错点,尽可能地多得分还是可能的。圆锥曲线中的易错点较多,本文主要从知识点方面来探寻其致误的原因及防范措施,以期对广大同学有所帮助和警示.知识点方面常见的易错点主要有以下几点:
一、忽视圆锥曲线定义中的条件致误
【例1】若动圆P过点N(-2,0),且与另一圆M:(x-2)2+y2=8外切,求动圆P的圆心的轨迹方程.
【错因分析】忽视双曲线定义中的条件“差的绝对值”,很容易错认为所求的轨迹就是整个双曲线.
【正确解析】因为动圆P过点N(-2,0),所以|PN|是动圆的半径.又因为动圆P与圆M相外切,所以|PM|=.故点P的轨迹是以M,N为焦点,实轴长为,焦距|MN|为4的双曲线的左支,则,故动圆P的圆心的轨迹方程为:
【防范措施】(1)熟记圆锥曲线的定义,要特别注意双曲线定义中的条件“差的绝对值”,搞清楚是整条双曲线还是仅为其中的一支;(2)认真审题,注意数形结合,多动手画示意图帮助判断.
【变式训练】已知B(5,0),C(-5,0)是△ABC的两个顶点,且,求顶点A的轨迹方程.
二、忽视离心率范围致误
【例2】已知点F1、F2分别是双曲线b>0)的左、右焦点,过点F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2为锐角三角形,则该双曲线离心率e的取值范围是( )
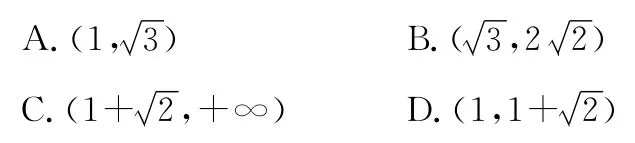
【错因分析】只考虑由不等关系解得的范围,而忽视双曲线离心率本身的取值范围.

【防范措施】在求圆锥曲线离心率的范围时,要注意不同曲线的离心率范围是不一样的,椭圆的离心率0<e<1,双曲线的离心率e>1,抛物线的离心率e=1,在由不等关系求出离心率的取值范围后,还要考虑和所在曲线本身离心率的取值范围取交集.

【参考答案】1<e<2.
三、焦点位置考虑不周致误
【例3】已知中心在原点,对称轴为坐标轴的双曲线的一条渐近线方程为4x-3y=0,并且焦点都在圆x2+y2=100上,求双曲线的标准方程.
【错因分析】忽视双曲线焦点的位置,想当然地认为焦点只在x轴上或只在y轴上,因考虑不全而犯“对而不全”的错误.


【防范措施】在求双曲线方程时,一定要注意全面考虑,不要漏解.若焦点位置不确定,则常用两种方法来解决:一是分类讨论,分别考虑焦点在x轴和y轴上的情形;二是设双曲线方程为的形式.若双曲线的渐近线方程为bx±ay=0时,则也可将双曲线方程设为的形式来求解,当λ>0时,焦点在x轴上,当λ<0时,焦点在y轴上.
【变式训练】若一抛物线的焦点在x-2y-4=0,求此抛物线的标准方程.
【参考答案】x2=-8y或y2=16x.
四、利用点差法解决中点弦问题时忽视判别式致误
【例4】已知双曲线2x2-y2=2,过点P(1,1)能否作直线l,使直线l与双曲线交于A,B两点,且线段AB的中点为P(1,1)?若存在,求出它的方程;若不存在,请说明理由.
【错因分析】利用点差法求出中点弦所在直线的斜率,并写出方程后,没有利用判别式来判断直线与双曲线是否有交点致误.
【正确解析】假设存在l,使得点P(1,1)为线段AB的中点.不妨设A(x1,y1),B(x2,y2),则有x1+x2=2,y1+y2=2.

2x2-4x+3=0,∵Δ=16-4×3×2=-8<0,∴此直线与双曲线无交点,与假设矛盾.
故这样的直线不存在.
【防范措施】点差法是解决圆锥曲线中点弦问题的快捷方法,但点差法使用的前提是以该点为中点的弦的斜率必须存在,因此利用此法求出弦所在直线方程时,必须要验证直线是否与曲线相交,即要验证判别式Δ的符号.
【参考答案】存在这样的直线l,其方程为2x+4y-3=0.
五、忽视特殊性、判断直线与圆锥曲线的位置关系致误
【例5】已知点A(0,2)和双曲线4x2-y2=4,则过点A(0,2)可作几条直线与双曲线有且只有一个公共点?
【错因分析】本题在设出直线方程与双曲线方程联立消元后,对方程的处理容易出错,容易忽视此方程的二次项系数为0的特殊情形,同时也容易忽视过点A(0,2)可向双曲线的两支作切线.
【正确解析】由题意可知直线的斜率必存在,故可设直线方程为y=kx+2,代入4x2-y2=4,整理得(4-k2)x2-4kx-8=0.
(1)当4-k2=0,即k=±2时,直线平行于渐近线,与双曲线只有一个公共点.
(2)当4-k2≠0,即k≠±2时,令Δ=(-4k)2-4(4- k2)(-8)=0,解得,此时直线方程为,与双曲线相切.故过点A(0,2)可作4条直线与双曲线有且只有一个公共点.
【防范措施】解决过定点的直线与双曲线位置关系问题的基本思路有两个,一是将直线方程与双曲线方程联立消元后,对所得方程进行讨论,要特别注意二次项系数为零的特殊情形,当二次项系数不为零时,借助判别式来讨论位置关系;二是利用数形结合思想,借助示意图来判断位置关系.在直线与圆锥曲线的位置关系中,双曲线和抛物线都有特殊情形,要特别注意.
【变式训练】过点A(4,0)的直线与抛物线:y2=-4x有且只有一个公共点,求直线的斜率k.
六、忽视直线斜率是否存在致误
【例6】在圆x2+y2=4上任取一点P,过点P作x轴的垂线段,D为垂足,点M在线段PD上,且点P在圆上运动.
(1)求点M的轨迹方程;
(2)过定点C(-1,0)的直线与点M的轨迹交于A,B两点,在x轴上是否存在点N,使为常数,若存在,求出点N的坐标;若不存在,请说明理由.
【错因分析】在解答本题时有两点容易造成失分:一是在构建方程及解方程的过程中,进行字符运算时容易失分;二是第(2)题中的求解过程中,忽视对斜率k的讨论而失分,常常出现会而不对、对而不全的情形.

【防范措施】(1)在加强思维能力培养的同时,还要重视运算能力的训练,平时要养成认真细心的运算习惯.(2)凡涉及直线与曲线的位置问题,只要直线的斜率不确定就要进行分类讨论,考虑斜率是否存在.当然,若直线在x轴上的截距为常数n时,也可以将直线方程设为x=my+n(m为参数),则可避免讨论斜率是否存在.
七、忽视判别式致误
【例7】已知中心在原点的双曲线的右焦点为(2,0),右顶点为,若直线与双曲线恒有两个不同的交点A和B,,且(其中O为原点),求k的取值范围.
【错因分析】容易忽视直线与椭圆相交需满足消元以后的一元二次方程的Δ>0.

【防范措施】解决直线与椭圆相交问题时,以下几点容易造成失分:(1)联立方程组前没能将方程中字母量减到最少,致使联立方程过多而失分;(2)忽视直线与椭圆相交需满足消元以后的一元二次方程的判别式Δ>0这一条件而失分.
【变式训练】直线l:y=kx+1,与双曲线2x2-y2=1的右支交于不同的两点A,B,求实数k的取值范围.
解决有关圆锥曲线的问题时,常常要根据曲线的几何性质,把曲线的几何特征转化为数量关系(如方程、不等关系、函数等),还要重视数形结合、等价转化、分类讨论、函数与方程等数学思想方法的应用。圆锥曲线内容对思维要求高,运算量大,所以失分也就多,除因知识点原因失分外,还要注意运算不过关也是失分的一大因素,所以在特别关注以上一些容易失分节点的同时,也还要高度重视数学运算能力的训练,平时要养成认真审题、细心书写的良好运算习惯,这也是减少失分的一个因素。高考数学不易,圆锥曲线部分得满分不易,愿同学们且学且珍重。
(作者单位:甘肃省临泽县第一中学)
