广义模糊粗糙集的包含度和相似度的生成

黄卫华, 杨国增

(1.文山学院 数学学院，云南 文山 663000; 2.郑州师范学院 数学与统计学院，郑州 450044)



广义模糊粗糙集的包含度和相似度的生成

黄卫华1, 杨国增2

(1.文山学院 数学学院，云南 文山 663000; 2.郑州师范学院 数学与统计学院，郑州 450044)

摘要：文献[1]把Pawlak粗糙集模型推广为广义模糊粗糙集模型.在文献[1]的基础上，讨论了广义模糊粗糙集上的包含度和相似度的生成，以及与其它模糊粗糙集模型的比较.

关键词：包含度；相似度；模糊粗糙集；生成

模糊集[2]理论是由美国著名控制论专家Zadeh在1965年提出的,粗糙集[3]理论则是由波兰华沙理工学院教授Z.Pawlak于1982年首次提出，粗糙集理论和模糊集理论都是研究信息系统中知识的不完善,不准确问题,将二者结合形成了模糊粗糙集.模糊粗糙集模型的推广也一直是RS理论研究的主流方向，目前主要有构造性方法和代数性(公理化)方法.本文是利用构造性方法推广了模糊粗糙集，并在此基础上研究了它的包含度和相似度的生成.

1预备知识

定义1[2]设L是非空集合X上的一个二元关系，满足：

(1)∀x∈X,(x,x)∈L；

(2)∀x,y∈X,(x,y)∈L,(y,x)∈L⟹x=y；

(3)∀x,y,z∈X,(x,y)∈L,(y,z)∈L⟹(x,z)∈L.

则L叫做一个偏序.

定义2[4]设(L,)是非空偏序集，若映射D:L×L→[0,1],对任意x,y,z∈L满足：

则称D为L上的包含度.

定义3[5]映射T：[0,1]2→[0,1]称为三角模，如果对任意a,b,c,d∈[0,1]满足：

(1)T(a,1)=a；

(2)T(a,b)=T(b,a)；

(3)T[T(a,b),c]=T[a,T(b,c)]；

定义4映射S：[0,1]2→[0,1]称为反三角模，如果对任意a,b,c,d∈[0,1]满足：

(1)S(0,a)=a；

(2)S(a,b)=S(b,a)；

(3)S[S(a,b),c]=S[a,S(b,c)]；

(4)S(a,b)S(c,d),(ac,bd).

定义5设X1,X2,…,Xn为论域，X=X1×X2×…×Xn，F(Xi)是Xi上模糊集合组成的集合，i=1,…,n.

(1)SM(x,x)=1；

(2)SM(x,y)=SM(y,x)；

定义7设(U,1)，(V,2)是两个非空偏序集，若映射g:U→V，对任意A1,A2∈U，当A11A2时，有g(A1)2g(A2)，则称g为保序映射.

定义8设(U,W,R)是模糊近似空间，X,Y是论域上的两个模糊集.

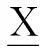
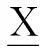
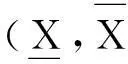
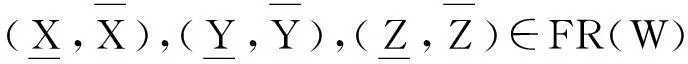
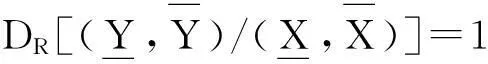
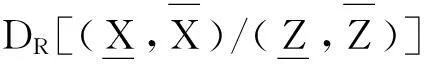
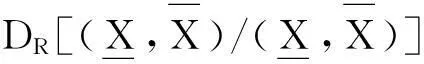
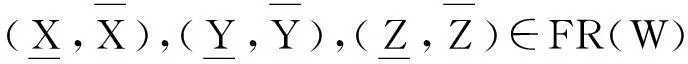
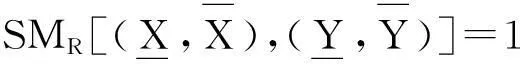
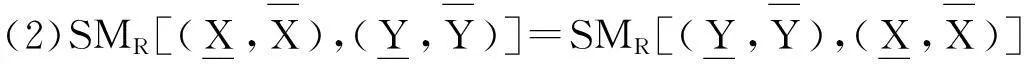
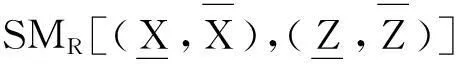
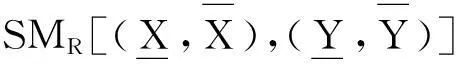
当X⊆RY⊆RZ时，SMR(X,Z)SMR(X,Y)∧SMR(Y,Z)，

称SMR为FR(W)上的强相似度.

2模糊粗糙集的包含度和相似度的生成

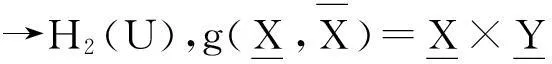
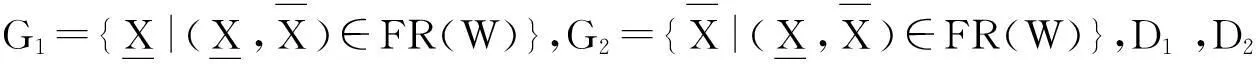
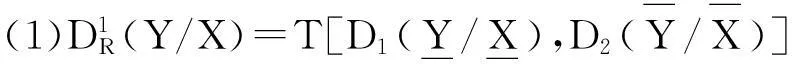
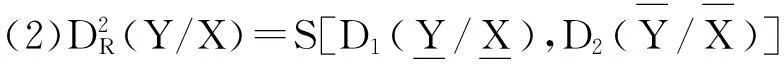
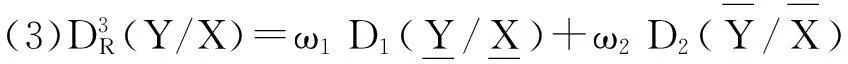
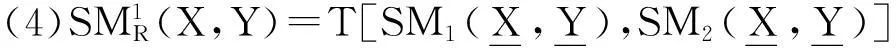
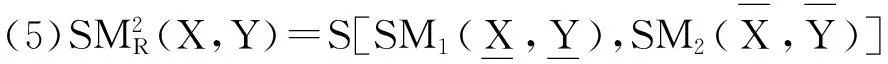
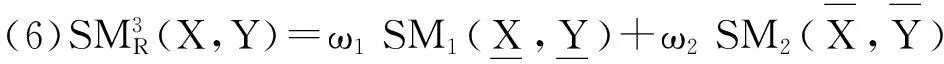
证明仅证明(1)和(3)

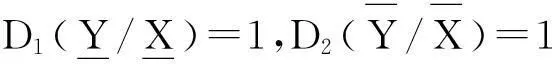
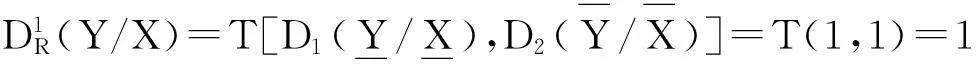
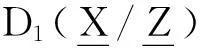
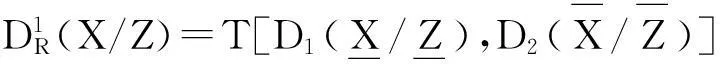
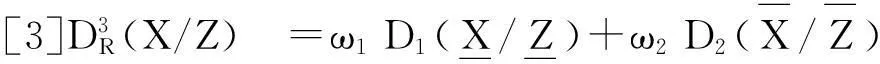
其余证明类似.

[参考文献]

[1]黄卫华，杨国增，李沫沫.一种广义模糊粗糙集模型的新定义[J].河南工程学院学报，2009(1)：45-47.

[2]HOWIEJM.Anintroductiontosemigrouptheory[M].NewYork：AcademicPress，1975.

[3]ZADEHLA.Fhzzysets[J].InformandControl，1965，8(3)：338-356.

[4]PAWLAKZ.Roughsets[J].InternationalJournalofComputerandInformationSciences，1982，11(5)：341-356.

[5]张文修，吴伟志.粗糙集理论与方法[M].北京：科学出版社，2000：3-10.

[责任编辑王新奇]

Generation of Inclusion Degree and Similarity ofGeneralized Fuzzy Rough Set

HUANG Wei-hua1, YANG Guo-zeng2

(1. School of Mathematics, Wenshan University, Wenshan 663000, China;

2. School of Mathematics and Statistics, Zhengzhou Normal University, Zhengzhou 450044, China )

Abstract：The rough set model is extended to the generalized fuzzy rough set model in reference [1]. In this paper, the generation of inclusion degree and similarity of generalized fuzzy rough set was discussed on the basis of the reference [1], and comparison with other fuzzy rough set model was carried out.

Key words：inclusion degree; similarity; fuzzy rough set; generation

中图分类号：O152

文献标志码：A

作者简介：黄卫华(1979—)，女，河南中牟人，文山学院数学学院讲师，硕士，主要从事信息代数、半群和粗糙集理论研究.

基金项目：云南省教育厅科学研究基金项目(2013Y585);文山学院重点学科数学建设项目(12WSXK01)文山学院高等代数精品课程

收稿日期：2015-08-25

文章编号：1008-5564(2016)01-0008-04