基于贝叶斯网络的协同过滤推荐算法

2015-08-06曹向前王平蒋凯聂世群田伟莉

软件导刊 2015年7期

关键词：相似度贝叶斯网络数据挖掘

曹向前　王平　蒋凯　聂世群　田伟莉

摘要：网络技术的快速发展产生了海量用户数据，为在海量数据中寻找与用户需求相符的数据，提出一种能快速得到较准确推荐结果的基于贝叶斯网络的协同过滤推荐算法。实验结果表明，与传统协同过滤推荐算法相比，该算法准确度更高。

关键词：贝叶斯网络；数据挖掘；相似度；协同过滤算法

DOIDOI：10.11907/rjdk.151098

中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2015）007-0064-02

0 引言

协同过滤推荐是根据基本用户的观点产生对目标用户的推荐列表。然而，随着数据量的增加，传统协同过滤算法的可扩展性问题逐渐凸现，根据贝叶斯网络的特点，当数据不断增加时，构建一个动态的贝叶斯网络不但能很好地解决这一问题，还能提高算法的准确性。

1 传统协同过滤算法

协同过滤算法通常分为3步[1-2]：①构建用户档案；②寻找最近邻，在用户档案中寻找与目标用户相似度最高的若干用户；③产生推荐。

1.1 建立用户档案（profile）

收集用户的评分、评价行为等，并进行数据清理、转换和录入，最终形成用户对各种项目的评价表，如表1 所示。

1.2 寻找最近居

计算用户与数据库内各用户的相似度，寻找最近邻居集。可采用以下方法：

（1）相关相似性。设用户i和a共同评分过的项目集合为Ii，Ia，则用户i和用户a之间的相似性sim（i，a）通过Peason 相关系数度量：

sim（i，a）=∑j∈Ii∩Ia（Ri，j-Ri-）（Ra，j-Ra-）∑j∈Ii∩Ia（Ri，j-Ri-）2∑j∈Ii∩Ia（Ra，j-Ra-）2（1）

（2）余弦相似性。用户评分看作n 维项目空间上的向量，用户间的相似性通过向量间的余弦夹角度量。设用户i和用户a在n维项目空间上的评分分别为向量i，a，则用户i和用户a直接的相似度sim（i，a）为：

sim（i，a）=cos（i，a）=i-×a-ia（2）

（3）修正的余弦相似性。余弦相似性度量方法中没有考虑不同用户的评分尺度问题，修正的余弦相似性度量方法通过减去用户对项目的平均评分改善了该缺陷。设用户i和a共同评分过的项目集合N，则用户i和用户a之间的相似性sim（i，a）为[3]：

sim（i，a）=∑j∈N（Ri，j-Ri-）（Ra，j-Ra-）∑j∈N（Ri，j-Ri-）∑j∈N（Ra，j-Ra-）（3）

1.3 预测

采用加权平均值方法，通过最近邻居集的评价产生推荐，推荐算法如下[4-5]：

pa，y=∑u∈NN，y∈Nsim（a，u）Ru，y∑u∈NN，y∈Nsim（a，u）（4）

pa，y=∑u∈NN，y∈Nsim（a，u）（Ru，y-Ru-）∑u∈NN，y∈Nsim（a，u）+Ra-（5）

Pa，y代表目标用户对项目 y 的预测值； Ru，y代表目标客户a最近邻居集内的用户u 对项目y 的评价。目标用户a 的最近邻居集用NN（nearest neighbor）表示，因此，u∈NN。

2 基于贝叶斯网络的协同过滤算法

在特征属性有条件独立或基本独立的条件成立时，传统协同过滤算法的准确率是最高的，但现实中各特征属性间往往条件并不独立，而是具有较强的相关性，这样就限制了其能力。所以必须考虑到各对象特征属性之间的关系，如能先根据对象的特征属性作出准确分类，再进行协同过滤，准确率就会有很大的提高，同时效率也会有很大的提高。

2.1 贝叶斯网络

贝叶斯网络是描述数据变量之间依赖关系的图形模式，是为处理人工智能研究中的不确定性问题而发展起来的。贝叶斯网表达了各节点间的条件独立关系，可以直观地从贝叶斯网当中得出属性间的条件独立以及依赖关系。此外，可以认为贝叶斯网用另一种形式表示出事件的联合概率分布，根据贝叶斯网的网络结构以及条件概率表，可以快速得到每个基本事件的概率。

通过贝叶斯网络，可以通过非独立对象的特征属性构建相应的贝叶斯网络拓扑关系图，再创建贝叶斯训练数据集，据此可将用户正确分类，再进行协同过滤推荐。

2.2 运用贝叶斯网络分类

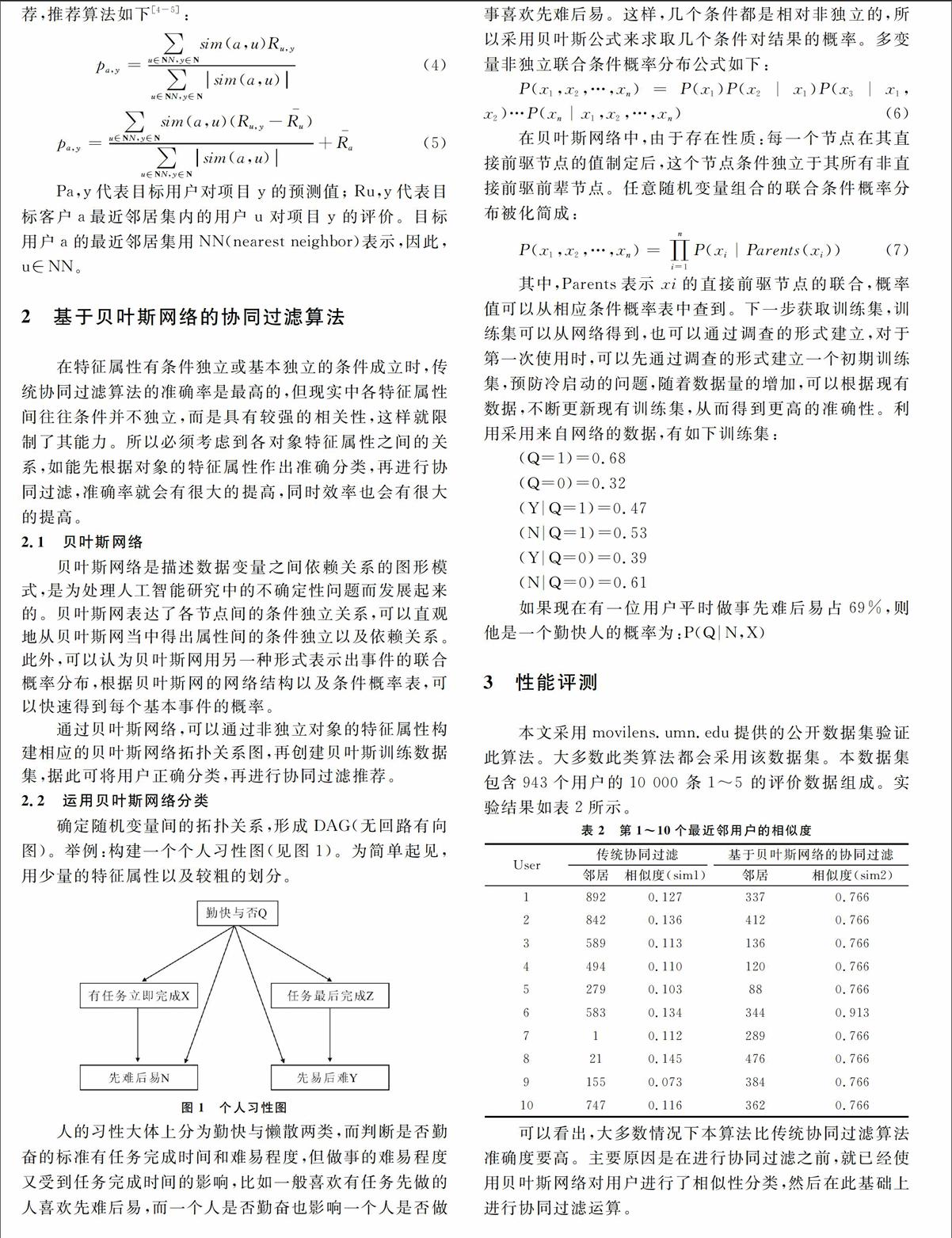
确定随机变量间的拓扑关系，形成DAG（无回路有向图）。举例：构建一个个人习性图（见图1）。为简单起见，用少量的特征属性以及较粗的划分。

图1 个人习性图

人的习性大体上分为勤快与懒散两类，而判断是否勤奋的标准有任务完成时间和难易程度，但做事的难易程度又受到任务完成时间的影响，比如一般喜欢有任务先做的人喜欢先难后易，而一个人是否勤奋也影响一个人是否做事喜欢先难后易。这样，几个条件都是相对非独立的，所以采用贝叶斯公式来求取几个条件对结果的概率。多变量非独立联合条件概率分布公式如下：

P（x1，x2，…，xn）=P（x1）P（x2|x1）P（x3|x1，x2）…P（xn|x1，x2，…，xn）（6）

在贝叶斯网络中，由于存在性质：每一个节点在其直接前驱节点的值制定后，这个节点条件独立于其所有非直接前驱前辈节点。任意随机变量组合的联合条件概率分布被化简成：

P（x1，x2，…，xn）=∏ni=1P（xi|Parents（xi））（7）

其中，Parents表示xi的直接前驱节点的联合，概率值可以从相应条件概率表中查到。下一步获取训练集，训练集可以从网络得到，也可以通过调查的形式建立，对于第一次使用时，可以先通过调查的形式建立一个初期训练集，预防冷启动的问题，随着数据量的增加，可以根据现有数据，不断更新现有训练集，从而得到更高的准确性。利用采用来自网络的数据，

有如下训练集：

（Q=1）=0.68

（Q=0）=0.32

（Y|Q=1）=0.47

（N|Q=1）=0.53

（Y|Q=0）=0.39

（N|Q=0）=0.61

如果现在有一位用户平时做事先难后易占69%，则他是一个勤快人的概率为：P（Q|N，X）

3 性能评测

本文采用movilens.umn.edu提供的公开数据集验证此算法。大多数此类算法都会采用该数据集。本数据集包含943个用户的10 000 条1～5 的评价数据组成。实验结果如表2所示。

可以看出，大多数情况下本算法比传统协同过滤算法准确度要高。主要原因是在进行协同过滤之前，就已经使用贝叶斯网络对用户进行了相似性分类，然后在此基础上进行协同过滤运算。

4 结语